- Deckungsgleich
- ist gleichbedeutend mit kongruent.
- Definitionsbereich
- Ist f :
A ®
B eine Funktion,
d.h. eine Zuordnung von der Menge A in die Menge
B,
so heißt die Menge A
ihr Definitionsbereich.
Man sagt auch, dass f auf der Menge
A definiert ist.
Ist f durch einen Term in einer Variablen
x
gegeben (siehe Termdarstellung),
so darf A nur solche
x-Werte enthalten,
für die der Term einen Sinn macht, d.h. wohldefiniert ist.
So darf zum Beispiel der Definitionsbereich für die Funktion
x ®
1/x die Zahl 0 nicht enthalten.
Als ihr Definitionsbereich kann daher
(im Rahmen der rellen Zahlen) die Menge der von Null verschiedenen
reellen Zahlen (oder eine Teilmenge davon) gewählt werden.
- Definitionslücke
- Es kann geschehen, dass ein Term an einer bestimmten Stelle nicht wohldefiniert ist,
aber durch eine nachträgliche Definition des fehlenden Funktionswerts zu einer
stetigen Funktion gemacht werden kann.
Wir sprechen dann von einer Definitionslücke, die "stetig geschlossen" werden kann, oder einer
hebbaren Singularität.
Beispiel: Die durch
f
 (x) =
(x2 + x)/x
zunächst bestehende Lücke an der Stelle x = 0 kann durch Kürzen
(wodurch sich der Term x + 1 ergibt) und die
nachträgliche Definition f (x) =
(x2 + x)/x
zunächst bestehende Lücke an der Stelle x = 0 kann durch Kürzen
(wodurch sich der Term x + 1 ergibt) und die
nachträgliche Definition f (0) = 1
stetig geschlossen werden. (0) = 1
stetig geschlossen werden.
Das Schließen von Definitionslücken allgemeinerer Funktionen
gelingt manchmal mit Hilfe der Regel von de l'Hospital,
der die Differentialrechnung zugrunde liegt
(siehe auch unbestimmte Form).
- Definitionsmenge
- Die Menge aller Elemente der zu einer Gleichung
gegebenen Grundmenge, für die beide Seiten der
Gleichung einen Sinn machen, d.h. mathematisch wohldefiniert sind.
Wird üblicherweise mit D bezeichnet.
So kann es beispielsweise bei
Bruchgleichungen passieren, daß
für manche Werte der Variablen eine Division durch Null auftritt.
Bei Wurzelgleichungen über der
Grundmenge der reellen Zahlen kann es passieren, daß
für manche Werte der Variablen die Wurzel aus einer negativen Zahl zu ziehen ist.
Werte, die derartige Probleme machen,
sind aus der Grundmenge herauszunehmen, um D
zu erhalten.
Da jede Lösung einer Gleichung in der Definitionsmenge liegt
(ansonsten könnte sie die Gleichung nicht zu einer wahren Aussage machen), ist
beim weiteren Vorgehen nur mehr sie zu beachten. Sie tritt an die
Stelle der ursprünglich
gegebene Grundmenge (die nun getrost vergessen werden
kann).
Achtung: Manchmal ist mit dieser Bezeichnung der Definitionsbereich
gemeint.
- Dekadischer Logarithmus
- ist ein anderer Name für den Zehner-Logarithmus.
- de l'Hospital, Regel von
- Siehe Regel von de l'Hospital.
- Dezimaldarstellung
- Darstellung einer reellen Zahl durch eine
(möglicherweise nicht-abbrechende) Abfolge von Ziffern, einen Dezimalpunkt ("Komma")
und ein Vorzeichen. Die Bedeutung der Ziffernfolge ist aus dem Beispiel
657.234... = 6 × 100 + 5 × 10 + 7 + 2/10 + 3/100
+ 4/1000 + ...
oder, in der modernen Potenzschreibweise,
657.234... = 6 × 102 + 5 × 101 + 7 × 10 0
+ 2 × 10 -1 + 3 × 10 -2
+ 4 × 10 -3 + ...
ersichtlich.
Die rationalen Zahlen (Zahlen, die als Brüche
"ganze Zahl/ganze Zahl" geschrieben werden können) sind genau jene reellen Zahlen, deren
Dezimaldarstellung entweder abbricht (d.h. ab irgendeiner Stelle nur aus Nullen besteht) oder
periodisch ist (d.h. ab irgendeiner Stelle nur mehr eine sich wiederholende Ziffernfolge
aufweist).
Beispiele: 33/25 = 1.32 = 1.320000000... ist eine abbrechende,
12/7 = 1.7142857142857142... eine periodische Dezimalzahl.
Reelle Zahlen, für die das nicht der Fall ist, heißen
irrationale Zahlen (wie z.B.
Ö2 = 1.414213562373095...
oder p = 3.141592653589793...).
Kleine Subtitität: Die Dezimaldarstellung ist nicht ganz eindeutig. So kann etwa
die Zahl 1 auch als 0.9999999... geschrieben werden, die Zahl 0.43 als
0.42999999...
Diese Mehrdeutigkeit betrifft aber nur den Fall, daß ab irgendeiner Stelle nur Neuner auftreten.
- Dezimalzahlen
- Siehe reelle Zahlen und Dezimaldarstellung.
- Diagonalverfahren
- heißt eine auf Georg Cantor zurückgehende Argumentation,
die beweist, daß die Menge der
reellen Zahlen
überabzählbar ist:
Wäre die Menge R
abzählbar, so könnte man ihre Elemente aufzählen, d.h.
als Liste x1,
x2,
x3, ... schreiben.
Nun kann für jede Liste aus reellen Zahlen eine weitere reelle Zahl
y konstruiert werden,
die in der Liste nicht vorkommt:
y muß sich nur von
x1 in der
ersten Nachkommastelle, von
x2 in der
zweiten Nachkommastelle, von
x3 in der
dritten Nachkommastelle ... unterscheiden. Damit ist gezeigt,
daß sich die Menge der reellen Zahlen nicht
als Liste schreiben lässt, also überabzählbar ist.
- Differential
- Dieses Wort wurde früher zur Bezeichnung infinitesimaler, d.h.
als "unendlich klein" gedachter Änderungen von Größen verwendet.
Mit ihrer Hilfe wurde die Ableitung einer Funktion
f º f(x)
als Differentialquotient
(d.h. als Quotient
df/dx
der Differentiale
df und dx)
angesehen. Auch in der Schreibweise für Integrale lebt diese Vorstellung weiter.
- Differentialquotient
- oder Differenzialquotient, ist ein anderer Name für die
Ableitung. Er rührt daher, dass früher die Ableitung einer Funktion
f º f(x)
als Quotient df/dx
der Differentiale
df und dx
angesehen wurde. Heute wird die Ableitung statt dessen als Grenzwert
des Differenzenquotienten
definiert. Der ältere Name und die Schreibweise
df/dx
für die Ableitung haben sich bis heute gehalten, sind aber nur mehr symbolisch gemeint.
- Differentialrechnung
- auch Differenzialrechnung ist jener Zweig der Mathematik, in dem
es um die Ableitung reeller Funktionen, ihren Eigenschaften
und den mit ihr verbundenen Methoden geht.
Der Ausgangspunkt zu ihrer Entwicklung war das Tangentenproblem.
Zusammen mit der Integralrechnung
ist sie Teil der Analysis.
- Differenz
- Siehe Subtraktion.
- Differenzenquotient
- Ist f eine reelle Funktion,
und sind x0 und x1
Zahlen, so dass f im gesamten
Intervall [x0, x1]
definiert ist, so heißt die Größe
(f(x1)
- f(x0))/(x1 -
x0) Differenzenquotient.
Geometrisch stellt er den Anstieg der Geraden (Sekante) durch die Punkte
(x0, f(x0))
und (x1, f(x1))
des Graphen von f dar
und kann als mittlere Änderungsrate von f
im Intervall [x0, x1]
interpretiert werden. Mit den Abkürzungen Dx = x1 - x0
und Df = f(x1) - f(x0)
schreibt er sich einfach als
Df/Dx,
was seinen Charakter als "Quotient von Differenzen" unterstreicht.
Zur Berechnung der Ableitung von f an der Stelle
x wird der Differenzenquotient auch in der Form
(f(x
+ e) - f(x))/e
angeschrieben, wobei e positiv oder negativ sein kann.
Der Grenzwert
e ® 0
dieser Größe ist - wenn er existiert -
die Ableitung f '(x).
- Differenzierbar
- an einer Stelle x0
heißt eine reelle Funktion f, wenn ihre
Ableitung an der Stelle x0
existiert. Die Formulierung "f ist differenzierbar"
(ohne weitere Angabe)
soll in der Regel ausdrücken, dass die Ableitung an jeder Stelle des Definitionsbereichs
existiert.
Ist eine Funktion auf der gesamten Menge R definiert,
und existiert die Ableitung an jeder Stelle, so nennt man sie auch
"überall differenzierbar".
Ist eine Funktion f an der Stelle x0
differenzierbar, so besitzt ihr Graph im Punkt
(x0, f(x0)
eine eindeutig bestimmte Tangente, die nicht zur vertikalen Achse
parallel ist (d.h. endlichen Anstieg hat).
Beispiele: Die Funktion x ® x3
ist überall differenzierbar.
Die Funktion x ® 1/x
ist in ihrem gesamten Definitionsbereich R*
( = Menge der
von 0 verschiedenen reellen Zahlen) differenzierbar.
Die Funktion x ® |x|
ist an der Stelle 0 nicht differenzierbar, an allen anderen Stellen schon.
Siehe auch stetig differenzierbar und Differenzierbarkeit, exakte Formulierung.
- Differenzierbarkeit, exakte Formulierung
- Die exakte Definition der
Differenzierbarkeit und der Ableitung
als Grenzwert von Differenzenquotienten
berücksichtigt, dass Folgen auf ganz verschiedene Weise einer
Stelle zustreben können, und dass die entsprechende Folge der Differenzenquotienten
jedesmal denselben Grenzwert haben muss. Eine alternative Formulierung benutzt
die exakte Sprache der Stetigkeit
von Funktionen.
- Differenzierbarkeit impliziert Stetigkeit
- Jede differenzierbare Funktion ist
stetig.
- Differenzieren
- Eine Funktion zu differenzieren heißt, ihre Ableitung zu bestimmen.
- Differenz zweier Vektoren
- wird komponentenweise berechnet. Ihre geometrische Bedeutung in der Pfeildarstellung
wird durch die Spitze-minus-Schaft-Regel ausgedrückt.
- Dimension
- ist die die maximale Zahl von Vektoren, die eine linear unabhängige Menge
bilden können. Die Menge aller n-komponentigen Vektoren,
zu identifizieren mit dem
R
 n,
hat Dimension n
(ist n-dimensional). n,
hat Dimension n
(ist n-dimensional).
- Dimensionsbehaftete Größen
- Siehe Einheiten.
- Dimensionslose Größen
- Siehe Einheiten.
- Diophantische Gleichungen
- werden Gleichungen genannt,
für die nur ganzzahlige
Lösungen gesucht werden, d.h. als deren
Grundmenge die Menge der ganzen Zahlen betrachtet wird.
Ein bißchen schlampig werden auch Gleichungsysteme,
für die nur ganzzahlige Lösungen gesucht werden, mit demselben Namen
bezeichnet.
Beispiel:
Gibt es ganze Zahlen x,
y, z,
für die
x2 +
y2 =
z2 ist? Außer dem trivialen Fall, daß eine
der drei Zahlen Null ist, gibt es noch unendlich viele Lösungen, z.B.
x = 3,
y = 4,
z = 5. Jede solche Lösung entspricht
- gemäß dem Satz von Pythagoras -
einem rechtwinkeligen Dreieck mit ganzzahligen Seitenlängen, wird daher auch
"Pythagoräisches Zahlentripel" genannt.
Demgegenüber hat das Gleichungssystem
xn +
yn =
zn,
wobei
n eine ganze Zahl > 2 ist,
keine Lösung, für die
x,
y und z
ganzzahlig und von Null verschieden wären. Das ist der Inhalt des berühmten
"großen Fermat'schen Satzes",
der von Pierre de Fermat im 17. Jahrhundert formuliert,
aber erst vor wenigen Jahren bewiesen wurde.
- Disjunkt
- heißen zwei Mengen A und B, die keine gemeinsamen Elemente besitzen.
Dies ist der Fall, wenn
d.h. wenn ihre Durchschnittsmenge
die leere Menge ist (kurz ausgedrückt:
wenn ihr Durchschnitt leer ist).
- Disjunkte Ereignisse
- oder einander auschließende Ereignisse sind Ereignisse,
deren (paarweise gebildete) Durchschnittsmengen leer sind, d.h. die nicht gleichzeitig eintreten können.
Für sie gilt die Additionsregel für disjunkte Ereignisse.
- Diskrete Wahrscheinlichkeitsverteilung
- Jedes Zufallsexperiment
mit endlich oder abzählbar vielen Versuchsausgängen
definiert eine diskrete Wahrscheinlichkeitsverteilung. Eine solche besteht aus der (endlichen oder unendlichen)
Liste p1, p2, p3...,
wobei pk die
Wahrscheinlichkeit des k-ten Ausgangs
ist. Ist eine Zufallsvariable gegeben, so können deren
Erwartungswert, Varianz und Standardabweichung
berechnet werden und geben einen gewissen Aufschluss über ihre statistischen Eigenschaften.
Beispiele für diskrete Wahrscheinlichkeitsverteilungen, die oft in Anwendungen auftreten, sind
die Binomialverteilung, die Poissonverteilung
und die hypergeometrische Verteilung.
- Diskrete Zufallsvariable
- ist eine Variable, die für jeden Versuchsausgang
des einer diskreten Wahrscheinlichkeitsverteilung zugrundeliegenden
Zufallsexperiments einen wohldefinierten reellen Wert annimmt.
Die gebräuchlichsten statistischen Kennzahlen von Zufallsvariablen
sind ihr Erwartungswert, ihre Varianz und
ihre Standardabweichung.
- Distributivgesetz
- auch Klammern ausmultiplizieren oder
Klammern auflösen genannt, ist die Rechenregel, die zeigt,
wie die Addition und die Multiplikation
miteinander verwoben sind. Für beliebige
Zahlen
x, y,
z gilt:
x ( y +
z ) =
x y +
x z.
Der Name kommt daher, daß sich die Multiplikation über die Summe ''verteilt''.
- Division
- ist in gewisser Hinsicht die ''Umkehrung'' der Multiplikation.
Der Quotient
x/y
( oder x/y)
ist definiert als die Antwort auf die Frage
''y × wieviel =
x?''
Diese Frage hat nur dann eine eindeutige Antwort, wenn
y ¹ 0 ist.
Jede Division stellt einen Bruch dar, und die Bedingung
y ¹ 0
bedeutet, daß der Nenner von 0 verschieden sein muß
(siehe Division durch 0).
Die Division (mit Nenner ¹ 0)
kann vollständig innerhalb der
Mengen der reellen,
rationalen, und komplexen
Zahlen ausgeführt werden - welche Körper genannt werden -,
führt jedoch aus den Mengen der
ganzen und der
natürlichen Zahlen heraus.
Aufgrund der Identität
kann jeder Quotient auch als Produkt geschrieben werden, wobei
der 1/y
der Kehrwert von
y ist.
- Division durch 0
- Wird versucht, eine Zahl x durch 0 zu
dividieren, also den Quotienten
x/0
zu berechnen, so ist die Frage
'' 0 × wieviel = x?''
zu beantworten. Falls
x ¹ 0 ist,
hat die Frage überhaupt keine Antwort. Falls
x = 0 ist, ist jede Zahl eine mögliche Antwort.
Dies zeigt, daß die Division durch 0 schlicht und einfach
nicht definiert, also eine mathematisch sinnlose Sache ist.
Auch die heuristische Frage ''Wie oft paßt 0 in
x?'' führt hier nicht weiter
(außer, daß sie zu der intuitiven Vorstellung führt,
1/0 habe etwas mit
''Unendlich'' oder ''minus Unendlich'' zu tun, und
0/0 sei völlig ''unbestimmt'').
- Dreieck
- genauer ebenes Dreieck, ist das zentrale Studienobjekt der Trigonometrie.
Die besondere Rolle von Dreiecken in der Geometrie rührt daher, dass beliebige durch Strecken oder Geraden begrenzte ebene Figuren
in Dreiecke zerlegt werden können.
Für die elementaren geometrischen Eigenschaften von Dreiecken siehe
Winkelsumme im Dreieck,
Höhen im Dreieck,
Umkreis eines Dreiecks,
Inkreis eines Dreiecks,
Schwerpunkt eines Dreiecks,
Eulersche Gerade,
Satz von Pythagoras,
Satz von Thales und
Flächeninhalt des Dreiecks.
Die wichtigsten auf der Verwendung von Winkelfunktionen beruhenden Methoden
zum Auflösen von Dreiecken (z.B. im Rahmen von Vermessungsaufgaben)
sind der Sinussatz und der Cosinussatz.
Für weitere Resultate der Dreiecksgeometrie siehe
Kongruenzsätze der ebenen Trigonometrie,
Ähnlichkeitssätze der ebenen Trigonometrie,
Kathetensatz,
Höhensatz,
Peripheriewinkelsatz,
Ungleichungen im Dreieck,
Trigonometrischer Monotoniesatz
und Tangenssatz.
Die Bezeichnungen von Eckpunkten, Seiten, Winkeln und Höhen in Dreiecken folgen, sofern nichts anderes gesagt wird, einer allgemeinen Konvention
(siehe Dreieck: Bezeichnungen).
Eine Verallgemeinerung bildet der Begriff des sphärischen Dreiecks.
- Dreieck: Bezeichnungen
- Zur Bezeichnung von Eckpunkten, Seiten, Winkeln und Höhen im Dreieck hat sich eine nützliche
Konvention herausgebildet, deren Gültigkeit angenommen werden kann, sofern nichts anderes gesagt wird:
Die Seitennamen a, b
und c werden im Gegenuhrzeigersinn vergeben,
die Eckpunkte mit den entsprechenden Großbuchstaben
A, B und C
bezeichnet, wobei A der Seite a
gegenüberliegt, usw.
Die (Innen-)Winkel werden mit a, b und g
bezeichnet, wobei a der Winkel beim Punkt
A ist, usw.
Die Höhe auf die Seite c wird meist mit
hc bezeichnet, usw.
Das gesamte Dreieck kann durch die Angabe der Eckpunkte mit dem Symbol DABC bezeichnet,
der Winkel a (dessen Scheitel der Punkt A ist) in der Form
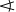 CAB
geschrieben werden. CAB
geschrieben werden.
- Dreieck, rechtwinkeliges
- Siehe rechtwinkeliges Dreieck.
- Dritte Wurzel
- oder Kubikurzel: siehe höhere Wurzeln.
- Durchschnittsmenge
- Sind A und B
zwei Mengen,
so ist die Durchschnittsmenge (kurz: der Durchschnitt)
A Ç B die Menge aller Elemente, die sowohl in
A als auch in B liegen:
|
A Ç B = { x | x Î A und x Î B }. |
|
Sie ist die Zusammenfassung aller gemeinsamen Elemente von A
und B.
- Durchstoßpunkt
- Falls eine Gerade im Raum mit einer Ebene
genau einen gemeinsamen Punkt besitzt, so wird dieser Schnittpunkt Durchstoßpunkt
genannt.
- Dyadischer Logarithmus
- ist ein anderer Name für den Zweier-Logarithmus.
|
|