| | |
| | | |
| |
| | |
| Empirische Verteilungen und ihre Kennzahlen |
| | | |
| |
| | |
Die Analyse von Daten, die aus der Beobachtung zufälliger Prozess gewonnen werden,
und ihre Beschreibung durch Kennzahlen (Mittelwert, empirische Varianz und
empirische Standardabweichung) ist
die Aufgabe der beschreibenden Statistik, der ein eigenes Kapitel gewidmet ist.
Oft beziehen sich unsere Beobachtungen auf die Häufigkeit, mit der gewisse Ereignisse eintreten.
Um derartige Beobachtungsdaten wird es nun gehen.
Relative Häufigkeitsverteilungen
| | | |
Beschreibende Statistik
(in Vorbereitung)
| |
| | |
Viele Dinge können beobachtet und ihn Form von Zahlen protokolliert werden.
In diesem Abschnitt geht es um Häufigkeitsverteilungen, die aus einer ganz bestimmten Art von Beobachtung
resultieren. Dabei wird ein (realer) Versuch, der bestimmte, beobachtbare Ausgänge haben kann, durchgeführt,
und es wird festgehalten, wie oft jeder einzelne Ausgang eingetreten ist.
Wir werden in diesem und im nächsten Abschnitt wiederholt drei Beispiele
heranziehen, in denen es um Häufigkeiten geht:
Beispiel 1: Es werden gleichzeitig zwei Würfeln geworfen und die Summe der Augenzahlen notiert. Dies wird oft wiederholt.
Die möglichen Ausgänge jedes einzelnen Versuchs sind die ganzen Zahlen von 2 bis 12.
Die in 30 Durchgängen gemessenen
Augenzahlen-Summen könnten so aussehen:
7, 6, 9, 10, 5, 4, 5, 11, 8, 6, 6, 8, 12, 9, 5, 6, 7, 3, 8, 6, 6, 7, 7, 7, 8, 4, 5, 5, 6, 9 (computergenerierte Liste).
Die dabei auftretenden Häufigkeiten:
Augenzahlen-
Summe | Anzahl |
| 2 | 0 |
| 3 | 1 |
| 4 | 2 |
| 5 | 5 |
| 6 | 7 |
| 7 | 5 |
|
|
Augenzahlen-
Summe | Anzahl |
| 8 | 4 |
| 9 | 3 |
| 10 | 1 |
| 11 | 1 |
| 12 | 1 |
|
Beispiel 2: Die Körpergrößen der 1235462 Einwohner eines Landes werden gemessen und
auf ganze Zentimeter gerundet.
Die Liste der Körpergrößen (auf ganze Zentimeter gerundet)
könnte so beginnen: 172, 153, 167, 152, 171, 183, 164, 158, 163, 172, 180, 169, 174, 176, 168, 158, 152, 163, 172,...
Die möglichen Ausgänge jedes einzelnen Versuchs sind ganzzahlige Zentimeterangaben.
Ein Ausschnitt der dabei auftretenden Häufigkeiten könnten so aussehen:
| Größe | Anzahl |
| 172 | 21804 |
| 173 | 22031 |
| 174 | 21767 |
| 175 | 21912 |
|
Beispiel 3: Die Kunden eines Einkaufszentrums werden an der Kassa gefragt, in welcher
Stadt sie wohnen.
Die möglichen Ausgänge jedes einzelnen Versuchs sind die Städte, aus denen Kunden kommen.
Wir nehmen an, es handelt sich dabei um Amselhain, Borkenstadt, Chromingen und Drosselfurt.
Die von 20 Kunden erhaltenen Daten könnten so aussehen:
D, A, A, D, C, B, D, C, C, C, A, D, D, C, D, B, C, A, D, B.
Die dabei auftretenden Häufigkeiten:
| Stadt | Anzahl |
| Amselhain | 4 |
| Borkenstadt | 3 |
| Chromingen | 6 |
| Drosselfurt | 7 |
|
Um eine einheitliche Schreibweise für die Häufigkeiten, die in derartigen Versuchen gewonnen werden,
zu verwenden, nennen wir die Zahl der Versuchsdurchführungen
n. Die möglichen Ausgänge
nummerieren wir in der Form 1, 2,
3,... durch.
Dazu müssen wir nun zwei Bemerkungen machen:
- Die Nummerierung wird lediglich dazu benutzt, um die verschiedenen Ausgänge zu benennen und voneinander zu unterscheiden.
Anstelle der Standardnummerierung 1, 2,
3,... können auch andere Formen verwendet werden.
Ob eine Nummerierung als Reihung sinnvoll ist, hängt ganz davon ab, was erhoben wurde und was interessiert:
Im obigen Beispiel 1 ist eine Nummerierung der Ausgänge von
2 bis 12 sinnvoll.
- In Beispiel 2 werden die Ausgänge am besten durch die
Zentimeterbeträge nummeriert, und
- in Beispiel 3 kommt es auf die Reihenfolge
gar nicht an. (Sie kann zum Beispiel alphabetisch gewählt werden:
Amselhain = 1,
Borkenstadt = 2,...).
- Die Zahl der möglichen Ausgänge muss im Prinzip nicht begrenzt werden.
Obwohl eine konkrete Beobachtung nur zu endlich vielen Daten führen kann,
kann es im Prinzip unendlich viele mögliche Ausgänge geben.
In drei unseren Beispielen ist das nicht der Fall, aber wenn etwa beobachtet wird, wie viele
Photonen pro Zeiteinheit auf ein Photoelement auftreffen, so hat es keinen Sinn, diese
Zahl nach oben zu begrenzen.
Ist in einer konkreten n-maligen Durchführung des Versuchs
- Ausgang 1 genau n1 mal eingetreten,
- Ausgang 2 genau n2 mal,
- Ausgang 3 genau n3 mal,
- usw. .....
so erhalten wir eine Liste absoluter Häufigkeiten
n1,
n2,
n3, ...
Unsere Schreibweise drückt aus, dass der Ausgang mit der Nummer k
genau nk mal eingetreten ist.
Die Summe all dieser Zahlen ist gleich der Anzahl der durchgeführten Versuchsdurchgänge:
In dieser Form liegen Häufigkeitsverteilungen zunächst vor. Wir nennen eine solche Liste
eine absolute Häufigkeitsverteilung.
Die absoluten Häufigkeitsverteilungen der obigen Beispiele sind:
- Beispiel 1: 0, 1, 2, 5, 7, 5, 4, 3, 1, 1, 1
- Beispiel 2: ..., 21804, 22031, 21767, 21912, ...
- Beispiel 3: 4, 3, 6, 7
| | | |
| |
| | |
Um zu den relativen Anteilen, die jeder Versuchsausgang auf sich vereinen kann, überzugehen,
definieren wir die relativen Häufigkeiten
h1 = n1 /n
h2 = n2/n
h3 = n3/n
............
|
|
(2) |
(was kurz auch in der Form
hk = nk/n
für alle k ausgedrückt werden kann).
Für die Summe dieser Zahlen erhalten wir nun
(die Summe aller relativen Häufigkeiten ist 1 -
wir nennen die Liste der relativen Häufigkeiten daher normiert) und jedes einzelne hk erfüllt
Die Liste
wird relative Häufigkeitsverteilung genannt (wobei der Zusatz "relativ" manchmal weggelassen wird).
Werden ihre Elemente mit 100 multipliziert, so drücken sie aus,
wie oft jeder Versuchausgang prozentuell eingetreten ist.
Die relativen Häufigkeitsverteilungen der obigen Beispiele sind:
- Beispiel 1: 0, 1/30, 1/15, 1/6, 7/30, 1/6, 2/15, 1/10, 1/30, 1/30, 1/30
- Beispiel 2: ..., 0.01765, 0.01783, 0.01762, 0.01774, ... (gerundet)
- Beispiel 3: 0.2, 0.15, 0.3, 0.35
Grafische Darstellung
| | | |
relative Häufigkeit
(in Vorbereitung)
| |
| | |
Wie können aus einer Liste relativer Häufigkeiten brauchbare Informationen gewonnen werden?
Für einen schnellen Überblick ist es sinnvoll, die Liste grafisch darzustellen.
Dafür stehen eine Reihe von Möglichkeiten zur Verfügung.
Eine schlanke Form der Darstellung ist der Punktgraph.
Für die in Beispiel 1 (Summe der Augenzahlen zweier Würfeln)
angegebenen Daten sieht er so aus:
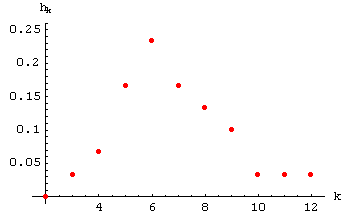
Beachten Sie, dass die Versuchsausgänge hier von
k = 2 bis k = 12
nummeriert sind. Das ist in diesem Fall sinnvoll, da jeder Ausgang die Summe der Augenzahlen zweier Würfeln darstellt.
Ein Punktgraph stellt eine Liste ähnlich dar wie ein Graph eine Funktion. Dabei spielt
die Nummer k der Ausgänge die Rolle der unabhängigen Variablen.
| | | |
Funktionsgraph
| |
| | |
Diesem Diagramm können wir (ohne uns mit den einzelnen Zahlen der Liste abplagen zu müssen) entnehmen,
dass die Summe der Augenzahlen eher öfter mittlere Werte annahm und eher selten die Randwerte.
Die am öftesten aufgetretene Augenzahlen-Summe war 6.
Neben der grafischen gibt es auch quantitative (rechnerische) Methoden, um relative Häufigkeitsverteilungen
genauer zu charakterisieren.
Den Mittelwert bilden - wovon?
| | | |
| |
| | |
Die populärste statistische Kenngröße ist der Mittelwert. Hat es
einen Sinn, im Zusammenhang mit einer relativen Häufigkeitsverteilung nach dem
Mittelwert zu fragen? Betrachten wir unsere drei obigen Beispiele:
- Beispiel 1: Hier können wir fragen: Wie groß ist der Mittelwert aller Augenzahlen-Summen, die aufgetreten sind?
Aufgrund der obigen grafischen Darstellung würden wir einen Wert etwa zwischen 5 und 8 vermuten,
denn dort sind die relativen Häufigkeiten am größten.
- Beispiel 2: In diesem Fall kann die Frage nach dem Mittelwert aller gemessenen Körpergrößen
gestellt werden.
- Beispiel 3: Hier erscheint die Frage nach dem Mittelwert auf den ersten Blick nicht sinnvoll!
Woraus sollte er auch gebildet werden? Ein Mittelwert einer Liste von Städten ist nicht wohldefiniert!
Andererseits kann beispielsweise gefragt werden, wie groß die Entfernungen sind, die die Kunden zum Einkaufen
zurücklegen. Einer derartigen Analyse müssten Entfernungen der vorkommenden Städte zugrunde gelegt
werden. Sie betragen:
| Stadt | Entfernung (km) |
| Amselhain | 10 |
| Borkenstadt | 14 |
| Chromingen | 6 |
| Drosselfurt | 6 |
|
Bei jeder Kundenbefragung könnte die entsprechende Entfernung notiert und am Ende
der Mittelwert aus allen notierten Entfernungen (einschließlich aller
Wiederholungen) gebildet werden. Das Resultat wäre als "mittlere Entfernung der Städte, aus denen die Kunden kommen"
ein gewisses Maß dafür, wie weit die Kunden angereist sind.
Diese drei Beispiele haben eines gemeinsam: Die Frage nach dem Mittelwert kann nur dann gestellt werden, wenn
jedem Versuchsausgang eine Zahl zugeordnet wird, die etwas Sinnvolles und Relevantes bedeutet
(Summe der Augenzahlen, Körpergröße, Entfernung der Stadt).
In allen Fällen hängt die Wahl dieser Zahlen davon ab, was man wissen möchte.
Aus ihnen kann dann, entsprechend der Häufigkeit des
Eintretens der einzelnen Ausgänge, der Mittelwert gebildet werden.
Dass es aber nicht immer sinnvoll ist, Mittelwerte zu bilden, zeigt dieses Beispiel!
Ganz allgemein bilden wir den Mittelwert einer gewissen Größe
(den Mittelwert der Augenzahlen-Summe, der Körpergröße,
der Entfernung der Stadt, aus der ein Kunde kommt).
Bezeichnen wir diese Größe mit a, so nimmt sie
für den Versuchsausgang k den Wert
ak an.
In unseren drei Beispielen haben die ak
folgende Bedeutungen:
- Beispiel 1: Hier ist die Größe a die Summe der Augenzahlen.
Werden die Ausgänge von
k = 2 bis k = 12
durchnummeriert, wobei k die Summe der Augenzahlen bedeutet, so ist
ak = k für alle k.
In diesem Fall kann der Nummerierungsindex k also mit der
Größe, die interessiert, identifiziert werden.
- Beispiel 2: Hier ist die Größe a die Körpergröße (in Zentimeter).
Werden die Ausgänge durch die Körpergröße durchnummeriert,
so gilt hier ebenfalls
ak = k für alle k.
Auch in diesem Fall kann der Nummerierungsindex k mit
Größe, die interessiert, identifiziert werden.
- Beispiel 3: Hier wählen die Größe a als die Entfernung
der Stadt, aus der ein Kunde kommt. Ihre Werte sind in der obigen Tabelle
festgelegt:
| aAmselhain = 10 |
| aBorkenstadt = 14 |
| aChromingen = 6 |
| aDrosselfurt = 6 |
Mit einer alphabetischen Durchnummerierung (Amselhain = 1,
Borkenstadt = 2,...) wird damit
a1 = 10,
a2 = 14,....
Würde man in diesem Fall die Nummerierung entsprechend den Werten
von a vornehmen, so könnten die Kunden aus Chromingen dann nicht von jenen aus Drosselfurt
unterschieden werden (und vielleicht möchte man diese Unterscheidungsmöglichkeit
erhalten, weil noch andere Untersuchungen geplant sind).
Fassen wir zusammen: In jedem unserer drei Beispiele haben wir nun
- eine Liste relativer Häufigkeiten hk (die relative Häufigkeitsverteilung) und
- eine Liste von Zahlen ak, die
eine Größe a abhängig vom
Versuchsausgang k annimmt.
Dies ist unser allgemeines Schema, und wir können uns nun der Frage zuwenden, wie
der Mittelwert von a berechnet wird.
Mittelwert
| | | |
| |
| | |
Ist also jedem Versuchsausgang k der Wert
ak der zu untersuchenden Größe
zugeordnet, so macht es Sinn, nach dem Mittelwert all dieser Werte ak
(entsprechend der Häufigkeit des Eintretens der einzelnen Ausgänge k)
zu fragen. Wir bezeichnen ihn mit
(ausgesprochen: "a quer" oder
"Mittelwert von a").
Er lässt sich mit Hilfe einer einfachen Formel berechnen, sofern die relativen Häufigkeiten
(5) bekannt sind:
Der Mittelwert von a ist durch
__
a
|
=
|
a1 h1 +
a2 h2 +
a3 h3 + ...
|
|
|
(7) |
| | | |
| |
| | |
gegeben.
Diese Formel stellt ein gewichtetes Mittel dar (wobei die relativen Häufigkeiten
hk
die "Gewichte" sind): Wie schwer ein ak
in dieser Summe "wiegt", hängt von hk
ab, d.h. davon, wie oft der Ausgang k
im Vergleich zu den anderen Ausgängen eingetreten ist.
Berechnen wir die Mittelwerte in unseren drei Beispielen: Der Übersicht halber sind die
Werte der Größe a (d.h. die Zahlen
ak) in
rot, die relativen Häufigkeiten
(d.h. die Zahlen hk)
in grün wiedergegeben:
- Beispiel 1: Die Anwendung von (7) ergibt:
__
a
|
=
|
2 × 0 +
3 × (1/30) +
4 × (1/15) +
5 × (1/6) +
6 × (7/30) +
7 × (1/6) +
8 × (2/15) +
9 × (1/10) +
10 × (1/30) +
11 × (1/30) +
12 × (1/30) = 41/6 » 6.833.
|
|
|
|
Der Mittelwert der Augenzahlen-Summe in den 30 Versuchsdurchgängen, aus denen unsere Daten stammen, ist
41/6, also etwas kleiner als 7.
Vergleichen Sie dieses Resultat mit der
obigen grafischen Darstellung! Unsere erste "gefühlsmäßige"
Schätzung hatte ergeben, dass sich der Mittelwert irgendwo zwischen 5 und 8 befindet.
- Beispiel 2: Wird (7) auf die erhobenen Daten
angewandt, so sieht ein Auschnitt der Berechnung so aus:
__
a
|
=
|
... + 172 × 0.01765 +
173 × 0.01783 +
174 × 0.01762 +
175 × 0.01774 + ...
|
|
|
|
Das Resultat ist dann die mittlere Körpergröße der Bevölkerung des betreffenden Landes.
- Beispiel 3: Die Anwendung von (7) auf unsere Daten ergibt:
__
a
|
=
|
10 × 0.2 +
14 × 0.15 +
6 × 0.3 +
6 × 0.35
= 8.
|
|
|
|
Die mittlere Entfernung, aus der die Kunden zum Einkaufen kommen, beträgt
8 km.
Aus diesen Beispielen geht also klar hervor, dass es sich nicht um "den Mittelwert einer gegebenen Verteilung" handelt,
sondern um den "Mittelwert von a"
entsprechend der gegebenen Verteilung.
Die Größe a kann dabei frei gewählt werden.
Sie geht lediglich in Form der Zahlen
ak ein.
Beispielsweise könnte anstelle von a auch
a2 gesetzt werden.
Der Mittelwert von a2
ist dann durch
__
a2
|
=
|
a12 h1 +
a22 h2 +
a32 h3 + ...
|
|
|
(8) |
gegeben, und ganz analog kann der Mittelwert von f(a)
gebildet werden, wobei f eine beliebige
Funktion ist:
___
f(a)
|
=
|
f(a1) h1 +
f(a2) h2 +
f(a3) h3 + ...
|
|
|
(9) |
Mit f(a) = a
wird daraus die Formel (7) für den Mittelwert von a,
mit f(a) = a2
ergibt sich (8) und für
f(a) = 1
erhalten wir, da klarerweise
ist, die Normierungsbedingung (3).
Wir wollen jetzt noch anmerken, dass das Bilden des Mittelwerts eine lineare Operation ist:
- Für jede fixe reelle Zahl c
gilt
___
ca
|
= c
|
__
a
|
. |
|
(11) |
In Worten: Der Mittelwert eines Vielfachen von a ist gleich dem
Vielfachen des Mittelwerts.
- Sind zwei Größen a und b gegeben,
die für jeden Versuchsausgang k Zahlenwerte
ak und
bk annehmen, so kann mit
Hilfe der Formel (7) auch der Mittelwert von b
gebildet werden, indem einfach
a und ak
durch
b und bk
ersetzt werden. Für die Mittelwerte dieser beiden Größen gilt dann
In Worten: Der Mittelwert einer Summe ist gleich der Summe der Mittelwerte.
Empirische Varianz und empirische Standardabweichung
| | | |
| |
| | |
Der Mittelwert (7) stellt in der Regel einen "ungefähren" oder "typischen" Wert einer
Größe a dar.
Er ist umso aussagekräftiger, je kleiner die "typische Abweichung"
der aufgetretenen a-Werte
von ihm ist. Um eine solche typische Abweichung zu definieren, greifen wir auf die Begriffe
der (empirischen) Varianz und der (empirischen) Standardabweichung zurück.
Die empirische Varianz einer Datenliste ist definiert als der Mittelwert der Quadrate der
Anweichungen der Einzeldaten vom Mittelwert. Das bedeutet: Zunächst wird der Mittelwert von
a mittels (7) berechnet.
Das "Quadrat der Abweichung vom Mittelwert" entspricht der Größe
f(a)
|
=
|
(
|
a
|
-
|
_
a
|
)2
|
. |
|
(13) |
| | | |
empirische Varianz
empirische Standardabweichung
| |
| | |
Wird sie in (9) eingesetzt, so ergibt sich die empirische Varianz von
a zu
s2
|
=
|
(a1 -
|
__
a
|
)2 h1 +
|
(a2 -
|
__
a
|
)2 h2 + ...
|
|
|
(14) |
Traditionsgemäß wird sie mit s2
bezeichnet, da sie stets ³ 0 ist.
Wir können sie auch in der Form
| |
|
__________ |
|
s2
|
= |
( |
a. |
- |
_
a2 |
)
| 2 |
|
|
|
(15a) |
anschreiben. Eine andere, dazu äquivalente Formel ist
s2
|
=
|
___
a2
|
-
|
(
|
_
a2
|
)
|
2
|
. |
|
(15b) |
| | | |
| |
| | |
In Worten: Die empirische Varianz von a
ist gleich dem Mittelwert von a2
minus dem Quadrat des Mittelwerts von a.
Anstelle von (14) kann daher auch
(8) berechnet und das Quadrad des Mittelwerts (7)
subtrahiert werden.
Die empirische Varianz drückt noch nicht die typische Abweichung von
a von seinem Mittelwert aus.
(So hat sie in Beispiel 3 die Dimension Quadratkilometer).
Ein Maß für die typische Abweichung der Größe
a vom ihrem Mittelwert
ist die empirische Standardabweichung von a,
auch (empirische) Streuung oder Schwankung von a genannt.
Sie ist s, also die Quadratwurzel
der empirischen Varianz (14)-(15b).
Die Bezeichnungen "empirisch" drücken aus, dass es sich hier um Kennzahlen
handelt, die aus empirisch gewonnenen Daten (d.h. aus einem realen
Zufallsexperiment) gewonnen werden.
Wir werden weiter unten entsprechende Größen ohne diesen Zusatz
kennen lernen, die sich nicht auf empirische Daten, sondern auf ideale
Zufallsexperimente beziehen.
Sehen wir uns nun noch die empirische Varianz und die empirische Standardabweichung in
unseren drei Beispiele an:
- Beispiel 1: Die Anwendung von (14) ergibt:
s2 = 757/180 » 4.206.
Daher ist s » 2.051.
Diese Zahl stellt die Streuung der im Experiment aufgetretenen Augenzahlen-Summen dar.
Vergleichen Sie dieses Resultat mit der
obigen grafischen Darstellung!
Gehen sie vom Mittelwert (ungefähr 7)
um 2 nach links und
um 2 nach rechts: In diesem Intervall
liegt ein Großteil der aufgetretenen Augenzahlen-Summen.
- Beispiel 2: Wird (14) auf die erhobenen
Daten angewandt, so ergibt sich mit s die Streuung der Körpergröße
in der Bevölkerung des betreffenden Landes.
- Beispiel 3: Die Anwendung von (14) auf unsere Daten ergibt:
s2 = 8.8.
Daher ist s » 2.966.
Diese Zahl stellt (in Kilometer) die Streuung der Entfernungen der Städte, aus denen die Kunden kommen, dar.
Neben dem Mittelwert, der empirischen Varianz und der empirischen Standardabweichung
gibt es noch weitere Kenngrößen für relative Häufigkeitsverteilungen
(wie etwa die "Schiefe", die misst, wie symmetrisch
die relativen Häufigkeiten um den Mittelwert verteilt sind
- sehen Sie sich etwa die Form der
oben grafisch dargestellten Verteilung noch einmal an!).
Wir wollen es aber bei den hier besprochenen bewenden lassen.
|
| | |
| |
| | |
| Diskrete Wahrscheinlichkeitsverteilungen |
| | | |
Zum Seitenanfang | |
| | |
Im vorigen Abschnitt haben wir empirische, d.h. durch tatsächliche Beobachtungen
erhaltene Häufigkeitsverteilungen und einige ihrer Kennzahlen besprochen.
Oft wollen wir aber mehr über die hinter einem Phänomen liegenden statistischen Gesetzmäßigkeiten
wissen. Dazu ist es nötig, ein reales Phänomen durch ein ideales Zufallsexperiment
zu modellieren. Das Kapitel "Wahrscheinlichkeitsrechnung und Statistik 1" war idealen
Zufallsexperimenten und den in ihnen auftretenden Wahrscheinlichkeiten gewidmet,
und auf diese mathematischen Konstruktionen greifen wir nun zurück.
| | | |
Zufallsexperiment
| |
| | |
Wir betrachten also ein ideales Zufallsexperiment, dessen mögliche Ausgänge mit 1, 2,
3,... durchnummeriert sind.
(Wieder kann die Nummerierung im Einzelfall von dieser Konvention abweichen).
Sein Ereignisraum (die Menge aller möglichen Ausgänge) kann daher in der Form
{1, 2, 3, ...}
angeschrieben werden.
Im ersten Kapitel über Wahrscheinlichkeitsrechnung und Statistik haben wir nur
Zufallsexperimente mit einer endlichen Zahl möglicher Ausgänge betrachtet.
Diese Bedingung wollen wir nun fallen lassen. Da die möglichen Ausgänge durchnummeriert werden
können, nennen wir unser Zufallsexperiment diskret. Sein Ereignisraum ist
entweder eine endliche oder eine abzählbare Menge.
Anmerkung: Es sind auch ideale Zufallsexperimente denkbar, für die jede reelle Zahl oder jede reelle Zahl eines Intervalls
einen möglichen Ausgang darstellt. Diese kontinuierlichen Zufallsexperimente
werden ein Thema des Kapitels "Wahrscheinlichkeitsrechnung und Statistik 3"
sein.
| | | |
Ereignisraum
abzählbar
kontinuierliche Zufallsexperimente
(in Vorbereitung)
| |
| | |
Wenn ab jetzt in diesem Kapitel eine Summe auftritt, die mit "+ ..." aufhört,
so ist damit gemeint, dass sie
- im Fall eines endlichen Ereignisraums abbricht und
- im Fall eines unendlichen Ereignisraums nicht abbricht, d.h. eigentlich keine Summe, sondern eine Reihe
darstellt.
Jeder Versuchsausgang k tritt mit einer gewissen
Wahrscheinlichkeit pk ein.
Unser Zufallsexperiment ist daher durch eine Liste
von Wahrscheinlichkeiten charakterisiert, die normiert sind
und für deren Elemente
gilt. Umgekehrt definiert jede Liste reeller Zahlen der Form (16), deren Elemente
(17) und (18) erfüllen,
ein diskretes Zufallsexperiment.
Eine derartige Liste wird eine diskrete Wahrscheinlichkeitsverteilung genannt.
Beachten Sie, dass relative Häufigkeiten, wie wir sie oben besprochenen haben,
die gleichen Beziehungen erfüllen. Es besteht eine enge Analogie:
| relativeHäufigkeitsverteilung |
Wahrscheinlichkeitsverteilung |
| (5) |
(16) |
| (3) |
(17) |
| (4) |
(18) |
| | | |
Reihen
| |
| | |
Das ist kein Zufall! Erinnern wir uns an die Definition der Wahrscheinlichkeit:
Wahrscheinlichkeiten sind Voraussagen für relative Häufigkeiten des
Eintretens von Ereignissen (für den Grenzfall einer gegen unendlich strebenden Anzahl
von Versuchsdurchführungen). Wird ein durch die Wahrscheinlichkeitsverteilung (16)
charakterisiertes Zufallsexperiment n mal durchgeführt,
so werden die dabei auftretenden Häufigkeiten
der Versuchsausgänge eine Liste vom Typ (5) bilden.
Wird n immer größer gemacht,
so wird die Liste (5) immer besser mit (16) übereinstimmen, und im (gedanklichen) Grenzfall einer
unendlichen Anzahl von Durchgängen gilt für jeden Ausgang
hk = pk.
| | | |
Definition der Wahrscheinlichkeit
| |
| | |
Beispiel: Wir modellieren das obige Beispiel 1:
Es werden gleichzeitig zwei Würfeln geworfen
Dabei setzen wir nun voraus, dass es sich um ideale Würfeln handelt, und dass
sie voneinander unabhängig sind, d.h. dass sie einander nicht beeinflussen.
Mit pk bezeichnen wir die
Wahrscheinlichkeit, dass die Summe der Augenzahlen k ist.
(Dabei kann k alle ganzzahligen Werte
zwischen 2 und 12
annehmen).
Indem zunächst alle Kombinationen von Augenzahlen betrachtet werden, wird dieses
Zufallsexperiment auf ein Laplace-Experiment (dessen Ausgänge alle gleich wahrscheinlich sind)
zurückgeführt: Es gibt 36 verschiedene
Kombinationen ("Zahl der möglichen Fälle"). Es ist nicht schwer, die Zahl der für den Ausgang
k "günstigen Fälle"
zu ermitteln (siehe den Button rechts).
Es ergibt sich
Augenzahlen-
Summe | Wahrscheinlich-
keit |
| 2 | 1/36 |
| 3 | 1/18 |
| 4 | 1/12 |
| 5 | 1/9 |
| 6 | 5/36 |
| 7 | 1/6 |
|
|
Augenzahlen-
Summe | Wahrscheinlich-
keit |
| 8 | 5/36 |
| 9 | 1/9 |
| 10 | 1/12 |
| 11 | 1/18 |
| 12 | 1/36 |
|
Diese Tabelle definiert die Wahrscheinlichkeitsverteilung für das Zufallsexperiment:
p2 = 1/36,
p3 = 1/18, ...
p12 = 1/36.
Ebenso wie relative Häufigkeitsverteilungen können Wahrscheinlichkeitsverteilungen
grafisch dargestellt werden. Der Punktgraph für das letzte Beispiel (Wahrscheinlichkeiten für
die Summe der Augenzahlen zweier Würfeln) sieht so aus:
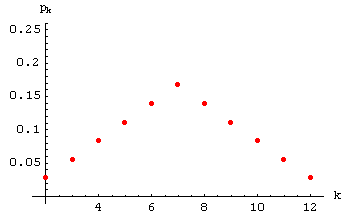
Vergleichen Sie ihn mit der oben wiedergegebenen
grafischen Darstellung der Häufigkeitsverteilung, die aus
30 Durchgängen im Real-Experiment
(Beispiel 1) gewonnen wurde!
Hätten wir nicht 30, sondern eine Million
Durchgänge durchgeführt, so wäre die relative Häufigkeitsverteilung
der (idealen) Wahrscheinlichkeitsverteilung schon sehr ähnlich gewesen.
Neben der grafischen gibt es auch quantitative (rechnerische) Methoden, um Wahrscheinlichkeitsverteilungen
genauer zu charakterisieren.
|
| | |
Statistische Unabhängigkeit
Laplace-
Experiment
der Augenzahlen-
Summen
| |
| | |
| Zufallsvariable, Erwartungswert, Varianz und Standardabweichung |
| | | |
Zum Seitenanfang | |
| | |
Wir besprechen nun einige Kenngrößen, die Wahrscheinlichkeitsverteilungen
charakterisieren. Wenn eine Wahrscheinlichkeitsverteilung die Voraussage
einer relativen Häufigkeitsverteilung
(für den Grenzwert unendlich vieler Durchgänge) ist,
so muss es möglich sein, in diesem Sinne auch den Mittelwert, die
empirische Varianz und die empirische Standardabweichung
einer vom Versuchsausgang abhängigen Größe a
vorauszusagen.
Diskrete Zufallsvariable
| | | |
| |
| | |
Die Größe a, die für
jeden Versuchsausgang k
eines Zufallsexperiments einen Wert ak besitzt,
bekommt nun einen Namen: Wir nennen sie eine diskrete Zufallsvariable.
Der Name rührt daher, dass wir sie uns als eine
"vom Zufall gesteuerte" Größe vorstellen können:
Wird das Zufallsexperiment durchgeführt, so tritt
ein Ausgang k ein,
und dementsprechend hat die Zufallsvariable den Wert
ak.
Da k aber nicht von
vornherein fest steht, hängt auch der Wert, den a
in diesem einen Versuch angenommen hat
(nämlich ak), vom Zufall ab.
Anmerkung: Wird im Zusammenhang mit einer Wahrscheinlichkeitsverteilung keine Zufallsvariable
definiert, so wird in der Regel davon ausgegangen, dass
sie mit dem Nummerierungsindex der Versuchsausgänge identifiziert wird, d.h. dass sie durch
ak = k
gegeben ist. In diesem Fall gibt die Wahrscheinlichkeitsverteilung unmittelbar die "Verteilung der Zufallsvariablen"
an.
Wird das Experiment sehr oft durchgeführt, so ergibt sich eine sehr lange Liste
von Werten, die a
in den einzelnen Durchgängen angenommen hat. Da im Fall einer gegen unendlich strebenden
Anzahl von Durchgängen die relativen Häufigkeiten gegen die
Wahrscheinlichkeiten streben, können die vorausgesagten Kennzahlen
mit Hilfe der bereits besprochenen Formeln ermittelt werden, indem lediglich
die relativen Häufigkeiten durch die Wahrscheinlichkeiten ersetzt werden.
Erwartungswert
| | | |
| |
| | |
Der (für eine gegen unendlich strebende Anzahl von Versuchsdurchführungen) vorausgesagte
Mittelwert einer Zufallsvariable a heißt
Erwartungswert von a,
angeschrieben in der Form
<a>,
und traditionsgemäß auch mit dem Buchstaben
m bezeichnet. Er wird berechnet, indem in
(7) einfach jedes
hk
durch
pk
ersetzt wird:
|
m º
< a>
|
=
|
a1 p1 +
a2 p2 +
a3 p2 + ...
|
|
|
(19) |
Eine andere verbreitete Bezeichnungsweise für den Erwartungswert von a ist
E(a).
Beachten Sie, dass diese Größe nun lediglich
- von den Werten der Zufallsvariable für die Versuchsausgänge (ak) und
- von den Wahrscheinlichkeiten, die das Zufallsexperiment charakterisieren (pk)
abhängt, aber nicht von Beobachtungsdaten. In diesem Sinne ist der Erwartungswert eine ideale
Größe.
Anstelle von a kann auch der Erwartungswert jeder anderen
Zufallsvariable berechnet werden. Bespielsweise ergibt sich in Analogie
zu (8)
|
< a2>
|
=
|
a12 p1 +
a22 p2 +
a32 p3 + ...
|
|
|
(20) |
(was manchmal auch in der Form E(a2)
geschrieben wird)
und ebenso kann in Analogie zu (9) der Erwartungswert
|
< f(a)>
|
=
|
f(a1) p1 +
f(a2) p2 +
f(a3) p3 + ...
|
|
|
(21) |
gebildet werden.
Mit f(a) = a
wird daraus die Formel (19) für den Erwartungswert von a,
mit f(a) = a2
ergibt sich (20) und für
f(a) = 1
erhalten wir, da
<1> = 1
ist, die Normierungsbedingung (17).
Beispiel: Der Erwartungswert der Summe der Augenzahlen zweier Würfel wird mit (19)
und der bereits oben ermittelten Wahrscheinlichkeitsverteilung zu
|
<a>
|
=
|
2 × (1/36) +
3 × (1/18) +
4 × (1/12) +
5 × (1/9) +
6 × (5/36) +
7 × (1/6) +
8 × (5/36) +
9 × (1/9) +
10 × (1/12) +
11 × (1/18) +
12 × (1/36) = 7.
|
|
|
|
berechnet.
(Der Übersicht halber sind die
Werte der Zufallsvariablen a in
rot und die Wahrscheinlichkeiten
in grün wiedergegeben).
Dieser Wert ist auch sehr schön an der obigen grafischen Darstellung der
Wahrscheinlichkeitsverteilung abzulesen.
Vergleichen Sie ihn mit dem Wert
41/6 » 6.833,
der sich oben für den Mittelwert der Augenzahlen-Summe in 30
Versuchsdurchgängen ergeben hat!
Manchmal wird vom "Erwartungswert einer Wahrscheinlichkeitsverteilung" gesprochen, ohne dass
von der betroffenen Zufallsvariablen die Rede ist. In diesem Fall wird, wie bereits erwähnt,
davon ausgegangen, dass
die Zufallsvariable mit dem Nummerierungsindex der Versuchsausgänge identifiziert wird,
d.h. dass sie durch
ak = k
gegeben ist.
Ebenso wie das Bilden des Mittelwerts (siehe (11) und (12)) ist das Bilden des Erwartungswerts eine lineare Operation:
- Für jede fixe reelle Zahl c gilt
|
< c a>
=
c < a>
|
. |
|
(22) |
In Worten: Der Erwartungswert eines Vielfachen ist gleich dem Vielfachen des Erwartungswerts.
- Für zwei Zufallsvariable a und
b gilt
In Worten: Der Erwartungswert einer Summe ist gleich der Summe der Erwartungswerte.
Varianz und Standardabweichung
| | | |
| |
| | |
Die (für eine gegen unendlich strebende Anzahl von Versuchsdurchführungen) vorausgesagte
empirische Varianz einer Zufallsvariable a wird
die Varianz (oder das Schwankungsquadrat) von a genannt (ohne den Zusatz "empirisch")
und ürblicherweise mit s2
bezeichnet. Durch Ersetzung der hk
durch die Wahrscheinlichkeiten pk
ergibt sie sich aus (14) zu
|
s2
|
=
|
(a1 - <a>)2 p1 +
(a2 - <a>)2 p2 + ...
|
. |
|
(24) |
Die zu (15a) und (15b) analogen Ausdrücke für sie sind
|
s2
=
< (a - <a>)2 >
=
< a2 > -
<a>2
|
. |
|
(25) |
In der Schreibweise mit dem Symbol "E" für den Erwartungswert lauten sie
E((a - E(a))2)
und
E(a2) - E(a)2.
Die Standardabweichung von a, auch
Streuung oder Schwankung genannt, ist
s, also die Quadratwurzel aus der Varianz.
Manchmal wird von "der Varianz (oder Standardabweichung) einer Wahrscheinlichkeitsverteilung" gesprochen, ohne dass
von der betroffenen Zufallsvariablen die Rede ist. In diesem Fall wird, wie bereits erwähnt,
davon ausgegangen, dass
die Zufallsvariable mit dem Nummerierungsindex der Versuchsausgänge identifiziert wird,
d.h. dass sie durch
ak = k
gegeben ist.
Beispiel: Die Varianz der Summe der Augenzahlen zweier Würfel wird mit (24)
und der bereits oben ermittelten Wahrscheinlichkeitsverteilung zu
s2 = 35/6
berechnet. Die Standardabweichung ist daher
s » 2.415.
Vergleichen Sie dieses Resultat mit der obigen grafischen Darstellung!
Nachdem wir nun die wichtigsten Eigenschaften diskreter Wahrscheinlichkeitsverteilungen diskutiert haben
und die Kennzahlen Erwartungswert, Varianz und Standardabweichung von Zufallsvariablen
berechnen können, wenden wir uns nun noch einigen in Anwendungen häufig auftretenden
Beispielen für diskrete Wahrscheinlichkeitsverteilungen zu.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Nehmen wir als Ausgangspunkt ein Zufallsexperiment, das zwei Ausgänge besitzt (ein so genanntes Bernoulli-Experiment):
- Das Ereignis A, das mit der Wahrscheinlichkeit
q eintritt und
- sein
Gegenereignis Ø A
(das daher mit der Gegenwahrscheinlichkeit
1 - q eintritt).
Dieses Experiment wird n mal durchgeführt.
Uns interessiert nun, wie oft das Ereignis A eintritt.
Die Wahrscheinlichkeit, dass A
genau k mal eintritt, ist durch
| | | |
Gegen-
wahrscheinlichkeit
| |
| | |
| pk
= qk (1 -
q)n - k |
⎛ |
n |
⎞ |
|
| ⎝ |
k |
⎠ |
|
(26) |
gegeben (wobei k alle ganzzahligen Werte zwischen
0 und n
annehmen kann). Dadurch wird für jedes
q und jedes
n
eine Wahrscheinlichkeitsverteilung definiert: die so genannte Binomialverteilung.
Ihre Zufallsvariable kann mit dem Nummerierungsindex der
Ausgänge identifiziert werden:
ak = k.
Ihre Rolle besteht lediglich darin, zu zählen, wie oft
A eingetreten ist.
Für unterschiedliche Werte von
q und n
(diese Größen werden auch die Parameter der Verteilung genannt)
ergeben sich unterschiedliche Verteilungen.
(Eigentlich müssten wir von "den Binomialverteilungen" sprechen).
Daher sind für die Wahrscheinlichkeiten
pk
in (26) auch Schreibweisen wie
pk(n, q)
oder
pk(n, q)
gebräuchlich.
Beispiel: Es wird mit einem Würfel 20 mal gewürfelt.
Uns interessiert, wie oft unter diesen 20 Würfen "Augenzahl 6" eintritt.
Die entsprechenden Wahrscheinlichkeiten
pk
(für k = 0
bis 20)
bilden eine Binomialverteilung (26) mit
q = 1/6 (die Wahrscheinlichkeit
für "Augenzahl 6" bei einmaligem Würfeln)
und n = 20.
Der Punktgraph der Verteilung (26) mit diesen Werten von
q und n sieht so aus:
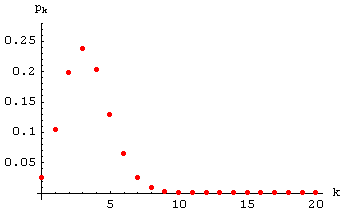
Ohne weitere Rechnung geht aus ihm hervor, dass die höchste Wahrscheinlichkeit für ein 3-maliges
Auftreten von "Augenzahl 6" besteht, und dass es sehr selten vorkommen wird,
mehr als 9 mal
"Augenzahl 6" zu werfen.
Der Erwartungswert und die Varianz der Binomialverteilung
(genauer: der Erwartungswert und die Varianz von k in der Binomialverteilung)
sind durch
|
m = qn
|
|
(27) |
und
gegeben.
Die Standardabweichung ist wie immer s, die Quadratwurzel aus der Varianz.
Der Erwartungwert könnte auch in der Form
<k>
geschrieben werden, die Varianz in der Form
<(k - <k>)2>
oder
<k2>
- <k>2.
Beispiel: Für das obige Beispiel (Binomialverteilung mit q = 1/6
und n = 20) ergibt sich
m = 10/3 » 3.333,
s2 = 25/9 » 2.778
und
s2 = 5/3 » 1.667.
Vergleichen Sie mit der grafischen Darstellung!
Für q = 1/2 ist die
Binomialverteilung symmetrisch. Hier ein Plot für q = 1/2
und n = 30:
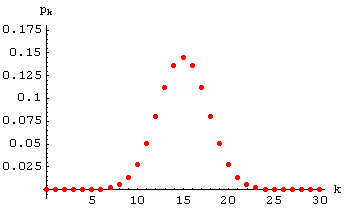
Der Erwartungswert ist in diesem Fall n/2.
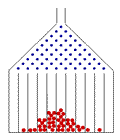Ein einfaches physikalisches Experiment, das auf die Binomialverteilung mit
q = 1/2 führt, ist
das Galton-Brett, in dem eine Kugel mehrere Reihen von Nägeln
passierten muss. Bei jedem Nagel kann sie (mit gleicher Wahrscheinlichkeit)
nach links oder nach rechts fallen.
Nachdem sie die Nagelreihen passiert hat, fällt sie in eines von mehreren Fächern.
Das Fach, in das sie schließlich fallen wird, hängt davon ab, wie oft
sie nach links bzw. rechts gefallen ist (unabhängig von der Reihenfolge, in der
sie das getan hat). Die Wahrscheinlichkeit für eine Kugel, in einem bestimmten Fach zu landen,
ist daher eine Binomialverteilung mit q = 1/2,
deren Parameter n
gleich der Zahl der Nagelreihen ist. Die tatsächliche Verteilung vieler Kugeln in den
Fächern wird näherungsweise eine Binomialverteilung sein.
Die der Binomialverteilung zugrunde liegende Situation kann auch anders formuliert werden:
Wir betrachten eine Menge von Objekten (z.B. Werkstücken in einer Produktion) und nehmen an,
ein relativer Anteil q
dieser Objekte besitze eine gewisse Eigenschaft (z.B. fehlerhaft zu sein).
Nun wird eine "Stichprobe vom Umfang n mit Zurücklegen"
gezogen, d.h. es wird n mal ein Objekt zufällig
herausgegriffen, auf die betreffende Eigenschaft untersucht und wieder zurückgelegt.
Die Wahrscheinlichkeit, dass dabei genau k mal
ein Objekt mit dieser Eigenschaft gezogen wird, ist durch (26)
gegeben. Diese Logik kann in der Werkstoffprüfung eingesetzt werden, denn mit ihrer Hilfe
lässt sich der Anteil q der fehlerhaften Stücke
abschätzen (wobei das
Zurücklegen natürlich ein bisschen ineffizient sein kann - schließlich geht
es ja auch um das Ausscheiden der fehlerhaften Stücke).
Wir werden weiter unten mit der "hypergeometrischen Verteilung"
auch Stichproben ohne Zurücklegen beschreiben können.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Aus der Binomialverteilung kann eine andere interessante Wahrscheinlichkeitsverteilung
gewonnen werden. Erinnern wir uns an den Prozess, der zur Binomialverteilung führt:
Ein Zufallsexperiment, das zwei Ausgänge
A (mit Wahrscheinlichkeit q) und
Ø A
besitzt, wird
n mal durchgeführt.
Dabei interessiert, wie oft A eintritt.
Nun stellen wir uns vor, dass das Experiment in jedem Zeitintervall
Dt
durchgeführt wird.
Dann können wir fragen, wie oft A innerhalb eines
größeren Zeitintervalls t eintritt.
Ist t = nDt,
so wird das Experiment während dieses Zeitintervalls
n mal durchgeführt. Die Wahrscheinlichkeit,
dass A während dieser
Zeit genau k mal eintritt, ist durch
die Binomialverteilung (26) gegeben.
Der Erwartungswert von k ergibt sich mit (27) zu
qt/Dt.
So oft wird A im Mittel
während einer Zeitspanne t eintreten.
Nun lassen wir
das Zeitintervall Dt und
die Wahrscheinlichkeit q gegen
0 streben, und zwar so, dass
der Quotient
l = q/Dt
endlich bleibt. Wird dieser Grenzübergang in der Binomialverteilung durchgeführt (was wir hier nicht
vorführen wollen), so ergibt sich die so genannte Poisson-Verteilung
Sie gibt die Wahrscheinlichkeit an, dass das Ereignis A innerhalb eines
Zeitintervalls der Länge t genau
k mal eintritt.
Wieder wird die Zufallsvariable mit dem Nummerierungsindex k
identifiziert. Dieser kann nun alle ganzzahligen Werte
³ 0
annehmen, ist also nicht auf einen endlichen Bereich beschränkt!
Da der Konstruktion der Poissonverteilung die Idee eines zeitlichen Ablaufs zugrunde liegt, spricht man auch von einem
Poissonprozess.
Die Größe l wird die Rate dieses
Prozesses genannt. Sie gibt an, wie oft A
pro Zeitintervall im Mittel eintritt.
Der Erwartungswert und die Varianz der Poissonverteilung
(genauer: der Erwartungswert und die Varianz von k in der Poissonverteilung)
sind gleich. Sie sind durch
|
m = s2 = lt
|
|
(30) |
gegeben.
Die Poissonverteilung modelliert Situationen, in denen viele voneinander unabhängige
Zufallsexperimente in sehr kurzen Zeitintervallen durchgeführt werden und jedes dieser
Experimente Anlass zum Eintreten des Ereignisses A sein kann.
Beispiele:
- Das physikalische Paradebeispiel für einen Poissonprozess ist der radioaktive Zerfall:
In einem Stück Materie sei eine sehr große Anzahl von angeregten Atomen enthalten, die
zerfallen können. Wann ein solches Atom zerfallen wird, entscheidet der Zufall, und zwar unabhängig
von allen anderen Atomen. Die Wahrscheinlichkeit, innerhalb eines gegebenen Zeitintervalls genau
k atomare Zerfälle zu registrieren, wird mit sehr guter
Genauigkeit durch eine Poissonverteilung (29) beschrieben.
- Die Zahl der Photonen (Lichtteilchen), die von einem heißen Körper wie der Sonne ausgesandt werden
und pro Zeitintervall auf ein Photoelement auftreffen, ist mit sehr guter Genauigkeit poissonverteilt.
- Die Zahl der täglich auf der Erde geborenen Babys ist (wenn Geburten als
hinreichend unabhängig von der Jahreszeit und ähnlichen Einflüssen erachtet werden)
mit guter Genauigkeit poissonverteilt.
Der Punktgraph der Poissonverteilung (29) für
lt = 7
sieht (im Bereich von
k = 0 bis 25 dargestellt)
so aus:
|
| | |
| |
| | |
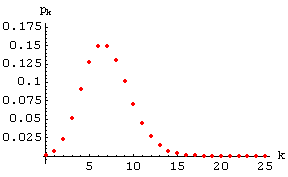
| Hypergeometrische Verteilung |
| | | |
Zum Seitenanfang | |
| | |
Erinnern wir uns an die oben erwähnte Anwendung der
Binomialverteilung in der Werkstoffprüfung: Dabei wird aus einer Menge
von Werkstücken, von denen ein relativer Anteil q
fehlerhaft ist, n mal ein
Werkstück herausgegriffen, auf Fehlerhaftigkeit untersucht und
wieder zurückgelegt. Effizienter ist es natürlich, eine Stichprobe vom Umfang
n ohne Zurücklegen
zu ziehen. Wie groß ist dann die Wahrscheinlichkeit, dass genau
k fehlerhalte Stücke zutage
treten?
Diese Frage wird durch die hypergeometrische Verteilung beantwortet. Sie ist definiert durch
| pk
= |
⎛ |
m |
⎞ |
|
⎛ |
N
- m |
⎞ |
, |
| ⎝ |
k |
⎠ |
⎝ |
n -
k |
⎠ |
|
| |
|
⎛ |
N |
⎞ |
|
|
| |
|
⎝ |
n |
⎠ |
|
|
|
(31) |
wobei k alle ganzzahligen Werte zwischen
0 und n
annehmen kann. Dabei ist
- N die gesamte Anzahl der Werkstücke (d.h. die Größe der Grundgesamtheit),
- m (£ N) die Zahl der fehlerhaften Stücke (deren relativer Anteil daher
q = m/N ist) und
- n der Umfang der Stichprobe (d.h. die Anzahl der ohne Zurücklegen herausgegriffenen Stücke).
Der Erwartungswert und die Varianz der hypergeometrischen Verteilung
(genauer: der Erwartungswert und die Varianz von k in der hypergeometrischen Verteilung)
sind durch
und
| s2
= |
mn
N |
|
( |
1 - |
m
N |
) |
|
N
- n
N -
1 |
|
|
(33) |
gegeben.
Hier ein Plot der hypergeometrischen Verteilung (31) für die Parameterwerte
N = 50,
m = 5 und
n = 10:
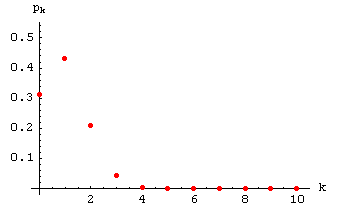
Wenn sich also unter 50 Werkstücken
5 fehlerhafte befinden und
10 Stichproben ohne Zurücklegen gezogen werden,
ist es sehr unwahrscheinlich, dabei alle 5 fehlerhaften
Stücke zu entdecken. Da der Erwartungswert
m = 5 × 10/50 = 1
ist, wird im Mittel mit dieser Methode nur ein fehlerhaftes Stück gefunden.
Durch die Auscheidung eines Stücks wird die Fehlerquote von ursprünglich 10%
lediglich auf 8.2% gesenkt.
Mit einer Wahrscheinlichkeit von etwas mehr als
0.3 wird mit dieser Methode überhaupt kein fehlerhaftes
Stück entdeckt!
Damit haben wir die Besprechung einiger in Anwendungen relevanter diskreter Wahrscheinlichkeitsverteilungen
beendet.
Für Berechnungen mit Verteilungen können Sie unser Tool
Online-Rechnen mit Mathematica
benutzen. Um Faktorielle oder Binomialkoeffizienten zu berechnen, geben Sie
beispielsweise 10! oder
Binomial[20,2] ein!
Um eine diskrete Wahrscheinlichkeitsverteilung in Form eines Punktgraphen darzustellen,
können Sie das (von unseren Innsbrucker Projektpartnern gestaltete) Online-Tool
Folgen
benutzen. Es gehört zwar zu einem anderen Kapitel der Mathematik, eignet sich aber
auch hierfür bestens.
Um beispielsweise die Binomialverteilung mit q = 1/6 und
und n = 20
darzustellen (das entspricht einem der oben gezeigten Diagramme), gehen Sie so vor:
- Rufen Sie den obigen Link auf und klicken Sie auf den Button "Applet starten"!
- Geben Sie unter a(n)= den Ausdruck für die
Verteilung ein. Hierbei müssen Sie zweierlei beachten:
- Der Index, der die Versuchsausgänge nummeriert, heißt in diesem
Tool n (während wir ihn bei unserer obigen Besprechung der diskreten
Wahrscheinlichkeitsverteilungen mit k bezeichnet haben).
- Bei der Eingabe müssen Sie Binomialkoeffizienten
durch Faktorielle ausdrücken, da kein eigener Befehl für Binomialkoeffizienten vorgesehen ist.
Für das Beispiel der Binomialverteilung geben Sie daher ein:
(1/6)^n*(1-1/6)^(20-n)*20!/(n!*(20-n)!)
- Lassen Sie das Feld Startwerte leer!
- Geben Sie unter Startindex 0 ein!
- Geben Sie unter Endindex 20 ein!
- Klicken Sie auf den Button "Berechnen" (rechts unten)!
Im erzeugten Graphen werden, im Gegensatz zu den in diesem Kapitel gezeigten, die Punkte durch Linien verbunden.
Als Alternative können Sie ein Tabellenkalkulationsprogramm wie Excel oder ein Computeralgebrasystem
verwenden.
Im Kapitel "Wahrscheinlichkeitsrechnung und Statistik 3" werden die hier entwickleten
Konzepte der diskreten Wahrscheinlichkeitsverteilung und Zufallsvariablen
auf den kontinuierlichen Fall ausgedehnt werden.
|
| | |
Binomialkoeffizienten und Faktorielle
kontinuierliche Zufallsexperimente
(in Vorbereitung)
| |