| | |
| | | |
| |
| | |
| Klassische und analytische Geometrie |
| | | |
| |
| | |
Geometrie zählt zu den ältesten Gebieten der Mathematik.
So wurden bereits in der Antike Fragen nach Längenverhältnissen in ebenen geometrischen Figuren,
aber auch nach Flächen- und Volumsinhalten gestellt. In der griechischen Antike haben auch die "Konstruktionen mit Zirkel und Lineal"
ihren Ursprung - im Rahmen der klassischen ("elementaren") Geometrie
bilden sie ein System von Darstellungs- und Beweismethoden, das wir heute als die
klassische "euklidische Geometrie" bezeichnen.
Dieser Art, Geometrie zu betreiben,
sind Sie wahrscheinlich in Ihrer bisherigen Mathematik-Ausbildung bereits begegnet.
Lesen Sie im nebenstehenden Exkurs die Zusammenfassung einiger besonders wichtiger
Themen aus der klassischen Geometrie:
- Strecken und Geraden
- Wissenswertes über ebene geometrische Figuren (Quadrat, Rechteck, Dreieck, Parallelogramm)
- Kongruenz
- Ähnlichkeit und der Strahlensatz
- Satz von Pythagoras ("Pythagoräischer Lehrsatz")
Sie werden in diesem
und in anderen Kapiteln vorausgesetzt und kommen bei Bedarf ohne weitere Erklärung als grundlegende Werkzeuge zum Einsatz.
| | | |
Themen aus der
klassischen
Geometrie
| |
| | |
Mit Pierre de Fermat (1601 oder 1607 - 1665) und vor allem
René Descartes (1596 - 1650) setzte eine neue (analytische = "zerlegende") Sichtweise
ein. Sie beruht auf der Idee des Koordinatensystems, das es gestattet,
die Position eines Punktes in der Ebene (bzw. im Raum) durch zwei (bzw. drei) Zahlen eindeutig zu bestimmen.
Lagebeziehungen zwischen Punkten können dann durch algebraische ("formelmäßige") Beziehungen ihrer Koordinaten ausgedrückt
werden. Damit ist es möglich, geometrische Sachverhalte und Probleme in algebraische
zu übersetzen (sehr oft handelt es sich dabei um Gleichungen oder Gleichungssysteme) und
rechnerisch zu lösen. Umgekehrt besitzen algebraische Probleme oft eine
geometrische Deutung.
Ausgangspunkt der analytischen Geometrie ist die
Charakterisierung von Punktmengen durch Gleichungen
| | | |

Koordinaten

Gleichungen

Gleichungssysteme
| |
| | |
Sehen wir uns das anhand zweier Beispiele an: Wie üblich bezeichnen wir die Koordinaten mit den
Buchstaben x und y
(obwohl natürlich auch beliebige andere Symbole zulässig sind).
Sei nun g die Menge aller Punkte der Zeichenebene, deren Koordinaten
(x, y) die Gleichung
erfüllen. Versuchen Sie, diese Definition wirklich zu verstehen, denn sie beinhaltet die wichtigste mathematische
Idee des gesamten Kapitels: g ist die Menge aller
Punkte, deren x- und y-Koordinaten
gleich sind.
Wenn wir "Punkte der Zeichenebene" mit "Zahlenpaaren" identifizieren, können wir
g als Menge anschreiben:
In Worten:
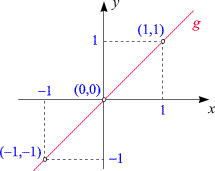 g ist die Menge aller reellen Zahlenpaare
(x, y), für die gilt:
x = y.
Nun stellen wir uns in Gedanken vor, alle diese Punkte seien rot dargestellt. Dadurch entsteht das nebenstehende Bild:
Bei der Menge g handelt es sich um eine Gerade.
Drei Punkte, die auf ihr liegen, sind hervorgehoben, und alle erfüllen die
Gleichung (1): Die x-Koordinate
ist gleich der y-Koordinate.
Dabei soll es uns nicht stören, dass die Linie, die in einer derartigen Skizze dargestellt wird,
eine endliche Dicke hat, und zudem nur ein endlicher Ausschnitt der Zeichenebene sichtbar ist.
Wichtig ist, was damit gemeint ist: g ist jene Gerade, auf der der Ursprung
liegt, und die unter einem Winkel von 45° (von "links unten" nach "rechts oben") ansteigt. Sie wird durch
die Gleichung (1) eindeutig bestimmt - weshalb wir
diese als Geradengleichung bezeichnen. (Es handelt sich bei ihr um eine
Gleichung in zwei Variablen). Ein bisschen formaler ausgedrückt:
g ist die Lösungsmenge der
Gleichung (1).
g ist die Menge aller reellen Zahlenpaare
(x, y), für die gilt:
x = y.
Nun stellen wir uns in Gedanken vor, alle diese Punkte seien rot dargestellt. Dadurch entsteht das nebenstehende Bild:
Bei der Menge g handelt es sich um eine Gerade.
Drei Punkte, die auf ihr liegen, sind hervorgehoben, und alle erfüllen die
Gleichung (1): Die x-Koordinate
ist gleich der y-Koordinate.
Dabei soll es uns nicht stören, dass die Linie, die in einer derartigen Skizze dargestellt wird,
eine endliche Dicke hat, und zudem nur ein endlicher Ausschnitt der Zeichenebene sichtbar ist.
Wichtig ist, was damit gemeint ist: g ist jene Gerade, auf der der Ursprung
liegt, und die unter einem Winkel von 45° (von "links unten" nach "rechts oben") ansteigt. Sie wird durch
die Gleichung (1) eindeutig bestimmt - weshalb wir
diese als Geradengleichung bezeichnen. (Es handelt sich bei ihr um eine
Gleichung in zwei Variablen). Ein bisschen formaler ausgedrückt:
g ist die Lösungsmenge der
Gleichung (1).
Diese Identifizierung der Geraden g
mit der Gleichung (1) ist so stark, dass sie uns verleitet
- ein bisschen schlampig - von
"der Geraden x = y"
zu sprechen. Etwas genauer können wir sagen: "Die Gerade g wird durch die Gleichung
x = y beschrieben
(oder dargestellt)".
In Aufgabentexten können Sie Formulierungen wie
"sei g die Gerade
x = y" oder die noch kürzere
Schreibweise
g: x = y
finden (womit einfach die Definition (2) gemeint ist).
Auf diese Weise kann
die geometrische Charakterisierung der Lage der Geraden
g durch die Angabe der Gleichung (1)
ersetzt werden.
Die Gerade, über die wir nun so ausführlich gesprochen haben, heißt übrigens
erste Mediane.
Als zweites Beispiel betrachten wir die Gleichung
| | | |

erste Mediane
| |
| | |
| | | |
| |
| | |
und
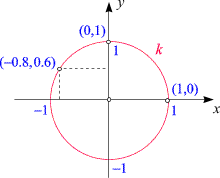 bezeichnen die Menge aller Punkte (x, y),
die sie erfüllen, mit k.
Denken wir uns wieder alle diese Punkte rot dargestellt, so entsteht das nebenstehende Bild.
Die Menge k ist eine Kreis (genauer: eine Kreislinie) mit Radius 1, dessen Mittelpunkt der Ursprung ist.
(Für den Beweis siehe den Button rechts).
Drei Punkte, die auf ihm liegen, sind hervorgehoben, und alle erfüllen die
Gleichung (3): Die Summe der Quadrate der beiden Koordinaten
ist gleich 1. Überprüfen wir das für den eingezeichneten Punkt mit Koordinaten
(-0.8, 0.6):
bezeichnen die Menge aller Punkte (x, y),
die sie erfüllen, mit k.
Denken wir uns wieder alle diese Punkte rot dargestellt, so entsteht das nebenstehende Bild.
Die Menge k ist eine Kreis (genauer: eine Kreislinie) mit Radius 1, dessen Mittelpunkt der Ursprung ist.
(Für den Beweis siehe den Button rechts).
Drei Punkte, die auf ihm liegen, sind hervorgehoben, und alle erfüllen die
Gleichung (3): Die Summe der Quadrate der beiden Koordinaten
ist gleich 1. Überprüfen wir das für den eingezeichneten Punkt mit Koordinaten
(-0.8, 0.6):
(-0.8)2 + 0.62 = 0.64 + 0.36 = 1.
Da die Gleichung (3) den Kreis k
eindeutig bestimmt, nennen wir sie eine Kreisgleichung.
Auch in diesem Fall ist es üblich, "vom Kreis
x2 + y2 = 1"
zu sprechen und die schriftliche Kurzform
k: x2 + y2 = 1
zu verwenden. Wie im Fall der Geraden kann auch hier die geometrische Charakterisierung der Lage des Kreises
k durch die Angabe der Gleichung (3)
ersetzt werden. Der Begriff des Kreises ist, wenn man so will, "algebraisiert" worden.
Der Kreis, den wir hier betrachtet haben, heißt übrigens Einheitskreis.
Ganz allgemein können wir eine beliebige Gleichung in zwei Variablen hinschreiben und die
Menge aller Punkte, die sie erfüllen, als Teilmenge der Zeichenebene betrachten.
Beispielsweise werden wir die Kurven, die durch Gleichungen wie
2x + 3y = 1,
y = 3x2
und
(x - 1)2 + y2 = 4
definiert sind, in diesem und den beiden nachfolgenden Kapiteln über analytische Geometrie kennen
lernen.
| | | |
| |
| | |
Weitere Beispiele:
Ist f eine reelle Funktion, so
können wir die Gleichung
betrachten. Sie sagt uns unmittelbar, wie groß die
y-Koordinate eines Lösungspunktes ist,
wenn seine x-Koordinate vorgegeben ist.
Welche Kurve beschreibt eine Gleichung dieser Art?
Falls Sie das erste Funktionen-Kapitel gelesen haben, sind sie bereits auf eine
derartige Konstruktion gestoßen: Es handelt sich um den Graphen der Funktion
f. Gleichung (1) ist von dieser Form
(es handelt sich um die lineare Funktion f(x) = x, deren
Graph eine Gerade ist), Gleichung (3) nicht.
Um sich Funktionsgraphen anzusehen, benutzen Sie einfach den mathe online Funktions-Plotter.
Um die durch (1) beschriebene Gerade zu reproduzieren, geben Sie den Funktionsterm x ein!
Umgekehrt können wir von einer Kurve ausgehen und fragen, ob es eine Gleichung
gibt, deren Lösungsmenge sie ist. Auf diese Weise kann eine große Klasse
von Kurven durch Gleichungen (genauer: als Lösungsmenge einer Gleichung in zwei Variablen
x und y)
beschrieben werden.
Rechnerische Lösung geometrischer Probleme
| | | |

Funktionsgraphen
| |
| | |
Eine typische Aufgabenstellung der analytischen Geometrie besteht darin, die Lage
der Schnittpunkte zweier Kurven zu bestimmen. Betrachten wir als Beispiel die beiden durch
(1) und (3) gegebenen Kurven. Die Idee der rechnerischen Umsetzung ist ganz einfach:
Welche Punkte liegen sowohl auf der Geraden g
als auch auf dem Kreis k?
Es ist dies klarerweise die Menge aller Punkte
(x, y), die
sowohl die Geradengleichung (1) als auch die Kreisgleichung (3) erfüllen.
Um sie zu ermitteln, muss also die Menge aller reellen Zahlenpaare (x, y)
gefunden werden, die das Gleichungssystem
erfüllen.
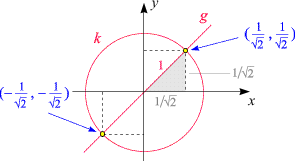 Die Schnittpunkte der beiden Kurven treten hier in der Sprache der analytischen Geometrie als
Lösungsmenge eines Gleichungssystems auf. Um es rechnerisch zu lösen,
nehmen wir die erste Gleichung beim Wort und
ersetzen in der zweiten Gleichung y
durch x. Wir erhalten die quadratische
Gleichung 2x2 = 1,
d.h. x2 = 1/2.
Sie besitzt die beiden Lösungen
x = 1/Ö2 und
x = -1/Ö2.
Die zugehörigen y-Koordinaten sind
y = 1/Ö2 für die erste und
y = -1/Ö2
für die zweite Lösung. Es gibt daher zwei Schnittpunkte mit den Koordinaten
(1/Ö2, 1/Ö2) und
(-1/Ö2, -1/Ö2).
In der Skizze sind diese Punkte und ihre Koordinaten dargestellt. Da unser Beispiel so einfach ist, hätten wir dieses Resultat auch durch
Anwendung des Satzes von Pythagoras auf das grau unterlegte Dreieck erhalten können.
(Ein Quadrat, dessen Diagonale die Länge 1 hat,
hat eine Seitenlänge von 1/Ö2).
Es illustriert aber sehr schön die Arbeitsweise der analytischen Geometrie: Geometrische
Sachverhalte werden durch algebraische Strukturen (in diesem Fall durch Gleichungen) beschrieben, geometrische Aufgabenstellungen
werden durch algebraische Verfahren (in diesem Fall durch das Lösen eines Systems aus zwei Gleichungen) bewältigt.
Theoretisch hätten wir die Lage der Schnittpunkte ermitteln können, ohne auch nur eine einzige Zeichnung zu
machen!
Die Schnittpunkte der beiden Kurven treten hier in der Sprache der analytischen Geometrie als
Lösungsmenge eines Gleichungssystems auf. Um es rechnerisch zu lösen,
nehmen wir die erste Gleichung beim Wort und
ersetzen in der zweiten Gleichung y
durch x. Wir erhalten die quadratische
Gleichung 2x2 = 1,
d.h. x2 = 1/2.
Sie besitzt die beiden Lösungen
x = 1/Ö2 und
x = -1/Ö2.
Die zugehörigen y-Koordinaten sind
y = 1/Ö2 für die erste und
y = -1/Ö2
für die zweite Lösung. Es gibt daher zwei Schnittpunkte mit den Koordinaten
(1/Ö2, 1/Ö2) und
(-1/Ö2, -1/Ö2).
In der Skizze sind diese Punkte und ihre Koordinaten dargestellt. Da unser Beispiel so einfach ist, hätten wir dieses Resultat auch durch
Anwendung des Satzes von Pythagoras auf das grau unterlegte Dreieck erhalten können.
(Ein Quadrat, dessen Diagonale die Länge 1 hat,
hat eine Seitenlänge von 1/Ö2).
Es illustriert aber sehr schön die Arbeitsweise der analytischen Geometrie: Geometrische
Sachverhalte werden durch algebraische Strukturen (in diesem Fall durch Gleichungen) beschrieben, geometrische Aufgabenstellungen
werden durch algebraische Verfahren (in diesem Fall durch das Lösen eines Systems aus zwei Gleichungen) bewältigt.
Theoretisch hätten wir die Lage der Schnittpunkte ermitteln können, ohne auch nur eine einzige Zeichnung zu
machen!
Mit Problemen dieser Art werden wir uns hier und in den beiden nachfolgenden Geometrie-Kapiteln beschäftigen.
Besonders die Techniken der Vektorrechnung, die in zwei weiteren Kapiteln behandelt werden,
stellen sich dabei als extrem nützlich heraus. Da die Vektorrechnung aber nicht in allen
Ausbildungswegen vorgesehen ist, treffen wir folgende Regelung:
- Für den Fall, dass die Vektorrechnung nicht zu Ihren Lerninhalten zählt,
stellen wir alle wichtigen Resultate dieses Kapitels auch ohne Vektorrechnung dar.
- Wir werden manche Resultate zwar auch in Vektorform hinschreiben, die Vektorrechnung
in diesem ersten Kapitel aber nur soweit verwenden, wie im
ersten Vektor-Kapitel dargelegt. Der Begriff des Skalarprodukts von Vektoren
wird im zweiten Vektorkapitel eingeführt und erst im zweiten Geometrie-Kapitel
zur Vereinfachung der Beschreibung von Geraden und Ebenen eingesetzt.
| | | |

Vektoren 1

Vektoren 2
| |
| | |
Auch wenn Sie nichts über Vektoren lernen müssen,
empfehlen wir Ihnen, sich von diesem Begriff nicht abschrecken zu lassen: Am einfachsten stellen Sie
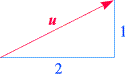 sich einen Vektor als einen "Pfeil" in der Ebene (bzw. im Raum) vor, der, ähnlich wie ein Punkt in Bezug auf
den Koordinatenursprung, zwei (bzw. drei) "Koordinaten" (oder "Komponenten") besitzt, und dessen Zweck es ist, eine Richtung anzugeben.
In der nebenstehenden Skizze ist der durch die Komponenten
2 und 1
definierte Vektor in der Ebene dargestellt. Nennen wir ihn u,
so können wir ihn in der kompakten Form u = (2, 1)
anschreiben. Eine andere, gleichwertige Form besteht darin, die beiden Zahlen übereinander
in der Form
sich einen Vektor als einen "Pfeil" in der Ebene (bzw. im Raum) vor, der, ähnlich wie ein Punkt in Bezug auf
den Koordinatenursprung, zwei (bzw. drei) "Koordinaten" (oder "Komponenten") besitzt, und dessen Zweck es ist, eine Richtung anzugeben.
In der nebenstehenden Skizze ist der durch die Komponenten
2 und 1
definierte Vektor in der Ebene dargestellt. Nennen wir ihn u,
so können wir ihn in der kompakten Form u = (2, 1)
anschreiben. Eine andere, gleichwertige Form besteht darin, die beiden Zahlen übereinander
in der Form
zu schreiben.
Die erste Zahl (hier 2) heißt x-Komponente, die zweite
Zahl (hier 1) heißt y-Komponente des
Vektors u.
Ein Punkt P mit Koordinaten
(3, 4) kann als Vektor
P = (3, 4)
aufgefasst werden. Er entspricht dem Pfeil vom Koordinatenursprung bis
P und wird in dieser Rolle "Ortsvektor" genannt.
Die Addition von Vektoren und das Bilden von Vielfachen geschieht komponentenweise:
(1, 2) + (3, 7) = (4, 9)
und 4 (2, 3) = (8, 12). (2, 3) = (8, 12).
Da die analytische Geometrie stark formalisiert ist, hat sie der Mathematik zu einem
neuen Maß an Präzision und Strenge verholfen. Das bedeutet aber nicht, dass die
geometrische Anschauung keinen Wert mehr besäße. Im Gegenteil:
Oft weist erst eine Zeichnung den Weg zu den nötigen Berechnungen.
Tipp: Machen Sie es sich zur Gewohnheit, die geometrischen Sachverhalte, mit denen Sie
konfrontiert sind, zeichnerisch zu skizzieren (auch dann, wenn es nicht ausdrücklich verlangt ist)!
Versuchen Sie stets, die Wechselbeziehungen zwischen geometrisch-anschaulichen
und algebraisch-abstrakten Sachverhalten zu verstehen.
Dieser Abschnitt sollte Ihnen eine erste Idee davon geben, was analytische Geometrie ist.
Im Folgenden werden wir Schritt für Schritt vorgehen und uns zunächst
mit der Darstellung von Geraden beschäftigen.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
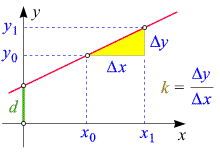
Um Geraden rechnerisch zu beschreiben, ist es notwendig, ein Maß für ihre Richtung zu haben.
Für Geraden in der Zeichenebene erfüllt der Begriff des Anstiegs diese
Funktion. Um ihn zu definieren, betrachten wir eine Gerade (die nicht parallel zur y-Achse
ist) und wählen auf ihr zwei (verschiedene) Punkte P und
Q. Wir bezeichnen die Koordinaten von
P mit
(x0, y0) und jene von
Q mit
(x1, y1).
Der Anstieg (die Steigung) k der Geraden ist definiert als der Quotient
| k |
= |
y1 - y0
x1 - x0 |
= |
Dy
Dx |
, |
|
(6) |
wobei
 Dx = x1 - x0
und Dy = y1 - y0
die Koordinatendifferenzen der Punkte P und Q
sind. Die nebenstehende Skizze illustriert, was das geometrisch bedeutet: Um von P nach Q zu gelangen, rückt man zunächst
entlang einer "horizontalen" (zur x-Achse parallelen) Strecke der Länge Dx
"nach rechts" und dann entlang einer "vertikalen" (zur y-Achse parallelen) Strecke der Länge Dy
"nach oben". Das so genannte Steigungsdreieck ist gelb hervorgehoben.
Dx = x1 - x0
und Dy = y1 - y0
die Koordinatendifferenzen der Punkte P und Q
sind. Die nebenstehende Skizze illustriert, was das geometrisch bedeutet: Um von P nach Q zu gelangen, rückt man zunächst
entlang einer "horizontalen" (zur x-Achse parallelen) Strecke der Länge Dx
"nach rechts" und dann entlang einer "vertikalen" (zur y-Achse parallelen) Strecke der Länge Dy
"nach oben". Das so genannte Steigungsdreieck ist gelb hervorgehoben.
Wichtig an dieser Definition ist nun, dass Formel (6) bei Verwendung beliebiger Steigungsdreiecke an derselben Geraden, d.h. bei beliebiger
Wahl der Punkte P und Q
(solange sie nur beide auf der Geraden liegen und voneinander verschieden sind), immer denselben Anstieg ergibt.
Beweis:
Die Unabhängigkeit des Anstiegs vom verwendeten Steigungsdreieck folgt unmittelbar aus dem Strahlensatz.
Verwenden wir zwei Steigungsdreiecke an derselben Geraden, um den Anstieg zu bestimmen, so verschieben wir sie,
wie diese Skizze zeigt,
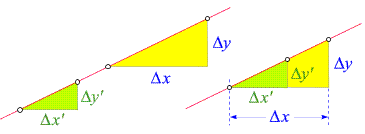 so, dass ihre linken Eckpunkte zur Deckung kommen. Der Strahlensatz (siehe den obigen Exkurs) besagt dann, dass
Dy/Dx = Dy'/Dx' gilt,
d.h. dass beide Steigungsdreiecke denselben Anstieg liefern.
so, dass ihre linken Eckpunkte zur Deckung kommen. Der Strahlensatz (siehe den obigen Exkurs) besagt dann, dass
Dy/Dx = Dy'/Dx' gilt,
d.h. dass beide Steigungsdreiecke denselben Anstieg liefern.
Wir können diesen Sachverhalt auch so formulieren: Alle Steigungsdreiecke an derselben Geraden sind
zueinander ähnlich.
Verläuft
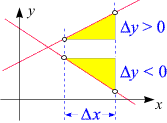 eine Gerade "von links unten nach rechts oben", so nennen wir sie an(steigend), da sie nach
"oben" führt, wenn man in die positive x-Richtung
voranschreitet.
Verläuft eine Gerade "von links oben nach rechts unten", so nennen wir sie ab(fallend).
Der Anstieg einer ansteigenden Gerade ist positiv, der Anstieg einer abfallenden Gerade ist negativ
(da sich für positives Dx im ersten Fall
ein positives Dy, im zweiten Fall
ein negatives Dy ergibt; siehe die nebenstehende Skizze).
eine Gerade "von links unten nach rechts oben", so nennen wir sie an(steigend), da sie nach
"oben" führt, wenn man in die positive x-Richtung
voranschreitet.
Verläuft eine Gerade "von links oben nach rechts unten", so nennen wir sie ab(fallend).
Der Anstieg einer ansteigenden Gerade ist positiv, der Anstieg einer abfallenden Gerade ist negativ
(da sich für positives Dx im ersten Fall
ein positives Dy, im zweiten Fall
ein negatives Dy ergibt; siehe die nebenstehende Skizze).
Die Anstiege einiger spezieller Geraden können wir ohne weitere Berechnung sofort ermitteln:
Der Anstieg einer um 45° geneigten,
ansteigenden Geraden ist gleich 1
(denn in diesem Fall gilt für jedes Steigungsdreieck Dx = Dy).
Der Anstieg einer "horizontalen" (zur x-Achse parallelen) Geraden ist
gleich 0
(denn dann gilt immer Dy = 0).
Und schließlich ist der Anstieg einer
um 45° geneigten, abfallenden Geraden
gleich -1
(in diesem Fall ist immer Dy = -Dx):
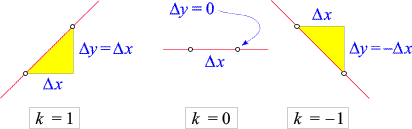
Achtung: Für eine "vertikale" (zur y-Achse parallele) Gerade
ist der Begriff des Anstiegs nicht definiert, d.h. sinnlos!
Eine anschauliche Deutung
 des Anstiegs ergibt sich, wenn wir uns die y-Koordinate
als "Höhe" und eine Gerade als Straße vorstellen, die auf- oder abwärts führt, wenn sie in positiver
x-Richtung befahren wird.
Die x-Koordinate gibt die Lage von Orten an,
wie sie auf einer Landkarte (also "von oben" betrachtet), erscheinen. Der Anstieg ist dann der
Höhenunterschied pro (in horizontaler Richtung) zurückgelegtem Weg.
Er ist ein offensichtliches Maß dafür, wie steil die Straße ansteigt bzw. abfällt. Ein ganz ähnliches Maß
wird im Autoverkehr tatsächlich verwendet, indem
der Höhenunterschied in Prozent des (in horizontaler Richtung) zurückgelegten Wegs
angegeben wird.
Eine Steigung von 30% entspricht einem Anstieg von
0.3.
des Anstiegs ergibt sich, wenn wir uns die y-Koordinate
als "Höhe" und eine Gerade als Straße vorstellen, die auf- oder abwärts führt, wenn sie in positiver
x-Richtung befahren wird.
Die x-Koordinate gibt die Lage von Orten an,
wie sie auf einer Landkarte (also "von oben" betrachtet), erscheinen. Der Anstieg ist dann der
Höhenunterschied pro (in horizontaler Richtung) zurückgelegtem Weg.
Er ist ein offensichtliches Maß dafür, wie steil die Straße ansteigt bzw. abfällt. Ein ganz ähnliches Maß
wird im Autoverkehr tatsächlich verwendet, indem
der Höhenunterschied in Prozent des (in horizontaler Richtung) zurückgelegten Wegs
angegeben wird.
Eine Steigung von 30% entspricht einem Anstieg von
0.3.
Eine wichtige Eigenschaft des Anstiegs ist, dass er die Richtung einer Geraden eindeutig charakterisiert: Zwei (nicht zur y-Achse parallele)
Geraden sind genau dann zueinander parallel, wenn sie den gleichen Anstieg haben.
Ein besonders praktisches ("normiertes") Steigungsdreieck ergibt sich, wenn Dx = 1
gewählt wird. Der Anstieg k kann dann durch
die Regel
charakterisiert
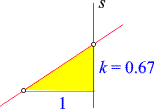 werden ("1-k-Regel"). Um damit auch negative Anstiege zu berücksichtigen, wird festgelegt, dass
(beispielsweise)
"um -2 hinauf gehen"
dasselbe bedeutet wie "um 2 hinunter gehen".
Auf diese Weise kann der Anstieg einer zeichnerisch gegebenen Geraden, wie in der nebenstehenden Skizze
gezeigt, bequem
als Abschnitt auf der Senkrechten s abgelesen
werden.
werden ("1-k-Regel"). Um damit auch negative Anstiege zu berücksichtigen, wird festgelegt, dass
(beispielsweise)
"um -2 hinauf gehen"
dasselbe bedeutet wie "um 2 hinunter gehen".
Auf diese Weise kann der Anstieg einer zeichnerisch gegebenen Geraden, wie in der nebenstehenden Skizze
gezeigt, bequem
als Abschnitt auf der Senkrechten s abgelesen
werden.
Anstelle des Anstiegs könnte man auch den Winkel a, den eine Gerade mit der x-Achse
einschließt (den Neigungswinkel) dazu benutzen, um ihre Richtung festzulegen.
Der Nachteil einer solchen Beschreibung wäre, dass es sich damit schlechter rechnen ließe.
Zwischen dem Neigungswinkel a einer Geraden (wenn er zwischen
-90° und
90°
angegeben wird) und ihrem Anstieg
k besteht eine Beziehung, die sich nicht durch
elementare Rechenoperationen auszudrücken läßt, die so genannte Tangensfunktion:
| | | |
| |
| | |
Darauf wird im Kapitel über die Winkelfunktionen näher eingegangen.
Die in der obigen Skizze eingezeichnete senkrechte Gerade s,
an der der Anstieg abgelesen werden kann, wird daher auch Tangens-Schiene genannt.
Das nebenstehende Applet verdeutlicht den Begriff des Anstiegs und des Steigungsdreiecks und stellt die Beziehung zum
Neigungswinkel her.
|
| | |

Tangens und der
Anstieg
Applet
Der Anstieg einer
Geraden
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wie wir oben besprochen haben, besteht ein Zusammenhang zwischen Punktmengen in der Zeichenebene und Gleichungen in
zwei Variablen x und y.
Um Geraden durch Gleichungen zu beschreiben, gibt es zwei Möglichkeiten.
Explizite Geradengleichung: y = k x + d
Jede Gerade (die nicht parallel zur y-Achse ist) kann durch eine Gleichung der Form
beschrieben werden. Überzeugen wir uns zuerst davon, dass eine Gleichung dieser Form immer eine Gerade darstellt
(d.h. eine Gerade als Lösungsmenge besitzt): Sind (x0, y0) und
 (x1, y1) zwei (verschiedene) Punkte
der Lösungsmenge, so gilt (definitionsgemäß) y0 = kx0 + d und
y1 = kx1 + d.
Daraus folgt unmittelbar
y1 - y0 = k(x1 - x0).
(Beachten Sie, dass die Konstante d weggefallen ist).
Lösen wir dies nach k auf, so ergibt sich für
k genau die Größe (6),
d.h. der Anstieg der Geraden durch die beiden gewählten Punkte. Das können wir mit
beliebigen Paaren von Punkten machen, deren Koordinaten die Gleichung (9) erfüllen,
und in jedem Fall stellt sich die Konstante
k als Anstieg der Geraden, auf der sie liegen, heraus.
Bei der Lösungsmenge von (9) muss es sich daher um eine Gerade mit Anstieg
k handeln.
(x1, y1) zwei (verschiedene) Punkte
der Lösungsmenge, so gilt (definitionsgemäß) y0 = kx0 + d und
y1 = kx1 + d.
Daraus folgt unmittelbar
y1 - y0 = k(x1 - x0).
(Beachten Sie, dass die Konstante d weggefallen ist).
Lösen wir dies nach k auf, so ergibt sich für
k genau die Größe (6),
d.h. der Anstieg der Geraden durch die beiden gewählten Punkte. Das können wir mit
beliebigen Paaren von Punkten machen, deren Koordinaten die Gleichung (9) erfüllen,
und in jedem Fall stellt sich die Konstante
k als Anstieg der Geraden, auf der sie liegen, heraus.
Bei der Lösungsmenge von (9) muss es sich daher um eine Gerade mit Anstieg
k handeln.
Auch die Bedeutung der Konstante d kann leicht erschlossen werden.
Sie ist der "Abschnitt auf der y-Achse"
(oder Ordinaten-Abschnitt; "Ordinate" ist einfach ein anderer Name für die vertikale Achse eines
rechtwinkeligen Koordinatensystems). Um das einzusehen, erinnern wir uns zunächst daran, dass für jeden Punkt auf der y-Achse
x = 0 gilt.
Um den Schnittpunkt der durch (9) beschriebenen Geraden mit der y-Achse
zu berechnen, setzen wir daher einfach x = 0 in (9) ein.
Wir erhalten y = d, was nichts anderes besagt, als dass
d die
y-Koordinate des gesuchten Schnittpunkts
ist.
| | | |

Ordinate
| |
| | |
Beispiele:
- Ein Beispiel für eine solche Darstellung einer Geraden haben wir bereits oben angeschrieben:
Gleichung (1), wenn sie in der Form
y = x gelesen wird.
Schreiben wir sie, noch ausführlicher, als
y = 1 x + 0,
so entpuppt sie sich als Spezialfall von (9) mit
k = 1 und
d = 0.
- Die Lösungsmenge der Gleichung y = 2x + 1
ist eine Gerade mit Anstieg 2, die im Punkt
(0, 1) die
y-Achse schneidet. (Nehmen Sie ein Blatt Papier und machen Sie eine Skizze, die
zeigt, wie sie relativ zum Koordinatensystem liegt!)
| | | |
| |
| | |
Ebenso
 wie der Anstieg k kann auch der Ordinaten-Abschnitt d negativ oder 0 sein:
wie der Anstieg k kann auch der Ordinaten-Abschnitt d negativ oder 0 sein:
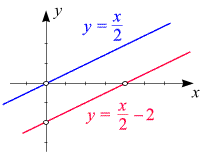
- Ist d < 0, so liegt der Schnittpunkt der Geraden mit der
y-Achse (dessen
y-Koordinate ja d
ist) unterhalb der x-Achse.
(Beispiel: Die rote Gerade mit der Gleichung y = x/2 -2
in der nebenstehenden Skizze).
- Ist d = 0, so lautet die Geradengleichung (9) einfach
y = kx.
Da sie für x = y = 0 erfüllt ist,
beschreibt sie eine durch den Ursprung gehende Gerade.
(Beispiel: Die blaue Gerade mit der Gleichung y = x/2
in der Skizze).
Ist eine Geradengleichung der Form (9) gegeben, so können wir daher allein den Vorzeichen der Koeffizienten
k und d
eine gewisse Grundinformation über die Lage der Geraden entnehmen.
| | | |
| |
| | |
Wie wir oben bereits bemerkt haben, stellen Gleichungen der Form (4) Funktionsgraphen dar.
Eine Gleichung der Form (9) beschreibt daher den Graphen der durch
f(x) = kx + d
definierten linearen Funktion f.
Genau genommen haben wir hier den Beweis geführt, dass der Graph einer linearen Funktion eine Gerade ist.
Diesem Sachverhalt haben wir es auch zu verdanken, dass wir den Funktions-Plotter benutzen
können, um uns diese Geraden anzusehen.
(Geben Sie zur Übung die Terme
x/2 - 2 und
x/2
ein!)
Da die Gleichung (9) uns "explitzit" (d.h. direkt, ohne Umweg) erlaubt, die
y-Koordinate jedes auf ihr liegenden Punktes aus der
x-Koordinate zu berechnen, wird sie
explizite Geradengleichung genannt.
Eine schöne Visualisierungsmöglickeit der Bedeutung der
Konstanten k und d
bietet unser Excel-Plotter.
Sie können in ihn den Term k*x + d
eingeben und die Werte von
k und d
dann mit dem Schieberegler variieren.
Halten wir weiters fest, dass Anstieg und Ordinaten-Abschnitt einer (nicht zur y-Achse parallelen) Geraden
durch deren Lage eindeutig bestimmt werden. Zwei Geraden, deren explizite Geradengleichungen
verschieden sind, sind verschieden. So sind beispielsweise die Geraden
g: y = 2x + 1
h: y = 2x - 1
zueinander parallel, da sie beide den Anstieg 2 haben, aber sie schneiden die
y-Achse in verschiedenen Punkten. (In welchen? Sehen Sie sich
die beiden Geraden im Funktions-Plotter an, indem Sie
als Funktionsterme 2*x + 1 und 2*x - 1 eingeben!)
Gerade durch zwei gegebene Punkte (Methode 1)
| | | |

lineare Funktion
| |
| | |
Ein oft auftretendes Problem besteht darin, die Gerade durch zwei vorgegebene Punkte
P(x0, y0)
und Q(x1, y1)
zu finden. Wir wollen anhand dieser Aufgabe demonstrieren, wie geometrische Probleme durch
Rechnung gelöst werden. Ist x0 ¹ x1
(was wir voraussetzen), so ist die gesuchte Gerade - wir nennen sie g - nicht parallel zur y-Achse und lässt sich
daher in der Form (9) schreiben. Um
k und d
zu berechnen, können wir verschiedene Wege einschlagen. Zwei davon sind:
- Weg 1: Wir schreiben die einzigen Informationen, die wir über g haben, an:
Die Punkte P und Q
liegen auf g, d.h. es gelten die Gleichungen
y0 = kx0 + d
und y1 = kx1 + d.
Sie bilden ein Gleichungssystem, das k und d
eindeutig bestimmt. (Versuchen Sie, es zu lösen! Es ist nicht schwierig.)
- Weg 2: Um k zu berechnen, benutzen wir einfach die Formel (6). Um
d zu finden, lösen wir die Bedingung, dass
P auf g liegt,
d.h. die Gleichung y0 = kx0 + d,
nach d auf und erhalten
d = y0 - kx0.
Damit sind k und d berechnet.
Beide Wege führen natürlich zum selben Resultat. Wir können es kurz und bündig so formulieren: Die Gerade durch die Punkte
P(x0, y0)
und Q(x1, y1) wird durch die Gleichung
| y |
= |
y1 - y0
x1 - x0 |
(x
- x0) + |
y0
|
|
|
(10) |
beschrieben. Sind die Koordinaten der Punkte P und Q
als konkrete Zahlen gegeben, so können wir einen der beiden beschriebenen Wege nachvollziehen oder in diese allgemeine Formel einsetzen.
Weiter unten werden wir im Rahmen einer gänzlich anderen Methode der Geradendarstellung eine weitere
Möglichkeit kennen lernen, diese Aufgabe zu lösen.
Implizite Geradengleichung: a x + by = c
| | | |
| |
| | |
Neben der expliziten gibt es noch weitere Möglichkeiten, Geraden durch Gleichungen darzustellen.
Dazu betrachten wir Gleichungen der Form
und setzen lediglich voraus, dass zumindest einer der Koeffizienten a und b
von 0 verschieden ist. Sehen wir uns
kurz die Lösungsmenge einer derartigen Gleichung an:
- Ist b ¹ 0,
so können wir beide Seiten durch b dividieren,
ohne damit die Lösungsmenge zu verändern und erhalten die Gleichung
(a/b)x + y = c/b.
Eine weitere Umformung führt auf die explizite Geradengleichung
y = -(a/b)x + c/b,
woraus sich durch Vergleich mit (9)
ergibt.
- Ist b = 0, so lautet die Gleichung
ax = c. Da laut Voraussetzung nun
a ¹ 0
ist, können wir beide Seiten durch a dividieren und
erhalten x = c/a.
Die Bedeutung dieser Gleichung liegt auf der Hand:
Die Menge aller Punkte, deren x-Koordinate
gleich einem vorgegebenen Wert (nämlich c/a) ist, bildet eine zur y-Achse
parallele Gerade.
In jedem Fall wird daher durch (11) eine Gerade dargestellt.
Umgekehrt kann jede Gerade der Zeichenebene (auch wenn sie zur y-Achse parallel ist)
in dieser Form dargestellt werden.
Neben der Benutzung von (12) gibt es noch eine andere, manchmal raschere Methode, die Lage einer Geraden,
die durch eine Gleichung vom Typ (11) gegeben ist, zu ermitteln:
- Da die x-Achse durch die Gleichung
y = 0 beschrieben wird, hat
der Schnittpunkt einer solchen Geraden mit der x-Achse
die x-Koordinate
c/a
(der Abszissen-Abschnitt).
- Da die y-Achse durch die Gleichung
x = 0 beschrieben wird, hat
der Schnittpunkt mit der y-Achse
hat die y-Koordinate
c/b
(der Ordinaten-Abschnitt).
Insbesondere Skizzen von Geraden sind mit diesen Informationen (den Achsen-Abschnitten) oft leichter anzulegen
als durch die Verwendung von k und d.
Der wichtigste Unterschied von (11) zur expliziten Form vom Typ (9) besteht
darin, dass erstere nicht eindeutig ist:
Es gibt viele verschiedene Gleichungen vom Typ (11), die dieselbe Gerade beschreiben!
So beschreibt beispielsweise die Gleichung
2x + 3y = 1
dieselbe Gerade wie
6x + 9y = 3
(denn sie ist ein Vielfaches der ersten).
Um aus einer Geradengleichung vom Typ (11) eine explizite Geradengleichung vom Typ (9)
zu erhalten, muss versucht werden, erstere nach y aufzulösen.
Daher wird (11) eine implizite Geradengleichung genannt:
Sie enthält zwar die Information, wie x und
y zusammenhängen, aber nicht in einer
nach y aufgelösten Form.
Das muss nicht immer funktionieren: Es klappt nur, wenn
b ¹ 0
ist. Um eine zur y-Achse parallele Gerade zu bschreiben,
kann (11) verwendet werden, während Geradengleichungen vom Typ (9)
sich dafür nicht eignen. Explizite Geradengleichungen sind daher eine Spur allgemeiner verwendbar als implizite.
Die Bezeichnungen "explizit" und "implizit" werden wir im zweiten Funktionenkapitel verwenden,
um diese zwei Formen der Darstellung auf beliebige Funktionen zu verallgemeinern.
| | | |

explizite und implizite Funktionsdarstellung
| |
| | |
Die Koeffizienten a und b
in (11) haben eine besondere Bedeutung. Sie beinhalten die Information über die Richtung
der Geraden. (Ist b ¹ 0,
so wird das durch die erste der beiden Formeln (12) ausgedrückt.
Auf noch einfachere Weise geben sie uns Auskunft über die Richtung normal zur Geraden:
Satz: Gehen wir von einem beliebigen
Punkt
- um a in die
x-Richtung (d.h. nach rechts oder links, je nach dem
Vorzeichen von a) und
- um
b in die y-Richtung
(d.h. nach oben oder unten, je nach dem Vorzeichen von b),
so haben wir uns insgesamt in eine Richtung normal auf die Gerade bewegt.
|
|
|
(13) |
Der durch die beiden Zahlen
a und b
definierte Bewegungsverlauf ist in der linken Skizze als Pfeil
dargestellt und mit n bezeichnet:
Diese Erkenntnis ist sehr wichtig! Versuchen Sie, sie mit Hilfe von Ähnlichkeitsüberlegungen
anhand der in der rechten Skizze dargestellten Dreiecke (für den Fall, dass
a, b
und c positiv sind), zu beweisen
(oder klicken Sie auf den nebenstehenden Button)!
| | | |
| |
| | |
Formulierung mit Vektoren: Für
den Fall, dass Sie bereits mit Vektoren vertraut sind, erwähnen wir, dass sich dieser Satz mit deren Hilfe einfacher ausdrücken
lässt: Der Vektor
steht
auf die durch (11) beschriebene Gerade normal und wird daher ein Normalvektor genannt.
(11) heißt auch Normalvektorform der Geraden.
Wir werden im zweiten Geometrie-Kapitel eine kürzere Schreibweise von (11),
die das so genannte "Skalarprodukt von Vektoren" verwendet,
und einige Anwendungen dieser Sichtweise kennen lernen. Zu einer Geraden gibt es viele Normalvektoren, aber alle sind zueinander parallel:
Jedes (von 0 verschiedene) Vielfache eines Normalvektors ist
wieder ein Normalvektor. Dem entspricht die Tatsache, dass jedes (von 0 verschiedene)
Vielfache einer Geradengleichung vom Typ (11) wieder eine solche Gleichung ist.
Damit haben wir die Methoden, Geraden als Lösungsmengen von Gleichungen in den Variablen
x und y,
d.h. in expliziter Form (9) oder in impliziter Form (11),
darzustellen, besprochen.
Daneben gibt es ein weiteres, gänzlich anderes Verfahren, und diesem wenden wir uns nun zu.
|
| | |

Normalvektorform
der Geraden
| |
| | |
| Parameterdarstellung von Geraden in der Ebene |
| | | |
Zum Seitenanfang | |
| | |
Wir kommen nun zu einer anderen Methode, Geraden mathematisch in den Griff zu bekommen. Sie ist in gewisser Weise
"konstruktiver" als die bisher besprochenen Verfahren, und einer ihrer Vorteile besteht darin, dass sie zur Beschreibung von Geraden im Raum (die wir
weiter unten behandeln werden) und von gekrümmten Kurven (die ein Thema des dritten Geometrie-Kapitels sind)
verallgemeinert werden kann.
Um sie einzuführen, stellen wir uns die Aufgabe, jene Gerade g
zu beschreiben, die durch zwei Bedingungen charakterisiert ist:
- Der Punkt A(x0, y0)
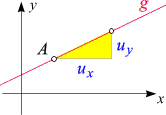 liegt auf g.
liegt auf g.
- Die Richtung von g wird durch zwei Zahlen ux und uy festgelegt,
von denen zumindest eine von 0 verschieden sein soll, und
die folgende Bedeutung haben:
Gehen wir von einem beliebigen Punkt von g aus
- um ux in die
x-Richtung und
- um uy in die y-Richtung,
so landen wir wieder auf g. Mit anderen Worten:
ux und uy
sind die Kathetenlängen eines Steigungsdreiecks
(sofern ux ¹ 0 ist).
Daraus folgt:
Ist ux ¹ 0,
so ist der Anstieg der Geraden durch
gegeben. Ist ux = 0,
so ist die Gerade parallel zur y-Achse.
| | | |

Analytische Geometrie 3
(in Vorbereitung)
| |
| | |
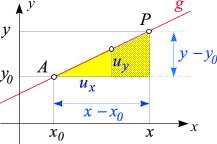 Nun sei P(x, y)
ein beliebiger Punkt auf g.
Ist er von A verschieden, so können wir
das durch A und P
definierte Steigungsdreieck betrachten: Es ist zu jenem Steigungsdreieck, das durch die Zahlen
ux und uy
gegeben ist, ähnlich (weil alle Steigungsdreiecke an eine Gerade zueinander ähnlich sind).
Die Längen entsprechender Seiten in den beiden Steigungsdreiecken unterscheiden sich nur durch einen
gemeinsamen Faktor, den wir t nennen.
Die Seiten des zweiten Steigungsdreiecks sind daher durch
Nun sei P(x, y)
ein beliebiger Punkt auf g.
Ist er von A verschieden, so können wir
das durch A und P
definierte Steigungsdreieck betrachten: Es ist zu jenem Steigungsdreieck, das durch die Zahlen
ux und uy
gegeben ist, ähnlich (weil alle Steigungsdreiecke an eine Gerade zueinander ähnlich sind).
Die Längen entsprechender Seiten in den beiden Steigungsdreiecken unterscheiden sich nur durch einen
gemeinsamen Faktor, den wir t nennen.
Die Seiten des zweiten Steigungsdreiecks sind daher durch
x - x0 = t ux ux
y - y0 = t uy uy
|
|
|
(16) |
gegeben. Aus diese beiden Gleichungen finden wir sofort x
und y. Wenn wir also den Faktor
t zwischen den Steigungsdreiecken kennen, ist es leicht,
die Koordinaten von P zu bestimmen.
Die wichtige Idee ist nun diese: Jeder Wert des Faktors t
entspricht einem möglichen Steigungsdreieck und daher einem Punkt P(x, y)
auf g. Damit drehen wir den Spieß um,
geben t vor und berechnen, welcher Punkt
P sich daraus ergibt:
x(t) = x0
+ t ux ux
y(t) = y0
+ t uy uy
|
|
|
(17) |
| | | |
| |
| | |
Dabei haben wir durch die Schreibweise angedeutet, dass x und
y von t
abhängen (d.h. Funktionen von t sind).
Betrachten wir diese Formeln und gehen wir noch einmal durch, was sie bedeuten. Sie drücken folgenden
Vorgang aus: Wir definieren den Punkt mit Koordinaten x(t) und
y(t) als jenen, zu dem wir kommen, wenn wir,
von A
 ausgehend,
ausgehend,
- um t
 ux in die
x-Richtung und ux in die
x-Richtung und
- um t
 uy in die y-Richtung uy in die y-Richtung
gehen. Ein Beispiel für einen solchen Punkt auf g
ist unser Startpunkt
A(x0, y0).
Seine Koordinaten erhalten wir aus (17), indem wir
t = 0 einsetzen.
Die nebenstehende Abbildung zeigt den Punkt P,
den wir für t = 2
erhalten.
Ganz allgemein können wir uns darauf verlassen, dass die Formeln (17)
für jeden Wert von t die Koordinaten eines Punktes auf
g angeben.
| | | |

Abhängigkeit
| |
| | |
Formulierung mit Vektoren:
Die beiden Ausdrücke (17) können in Vektorschreibweise in der Form
| x(t)
= |
⎛ |
x0 |
⎞ |
+ |
t |
⎛ |
ux |
⎞ |
| ⎝ |
y0 |
⎠ |
⎝ |
uy |
⎠ |
|
(18) |
zusammengefasst werden, wobei x für den Ortsvektor
des Punktes (x, y), d.h. für den Pfeil vom Ursprung
bis zum Punkt (x, y) steht.
x(t) steht daher für
(x(t), y(t)).
Noch kürzer kann dies in der Form
ausgedrückt werden, wenn die Abkürzungen A = (x0, y0)
und u = (ux, uy)
verwendet werden (wobei es gleichgültig ist, ob die Komponenten eines Vektors untereinander oder
nebeneinander geschrieben werden).
u heißt
Richtungsvektor der Geraden.
A ist der
Ortsvektor des gegebenen Punktes A, der auf der Geraden liegt:
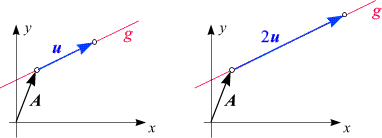
Die beiden Skizzen zeigen den "Weg", auf dem man vom Ursprung aus zu den Punkten mit Ortsvektoren
A + u
(entspricht t = 1)
und
A + 2 u
(entspricht t = 2)
gelangt. Beide liegen auf der Geraden g. u
(entspricht t = 2)
gelangt. Beide liegen auf der Geraden g.
Umgekehrt gibt es für jeden Punkt auf g
einen Wert von t, so dass (17) seine Koordinaten sind.
Die Variable t heißt
Parameter (Betonung: Parameter),
und (17) bzw. (18) oder die Kurzform (19) heißt Parameterdarstellung (oder Parameterform) der Geraden
g.
Durchläuft der Parameter t die Menge der reellen Zahlen, so durchläuft
der Punkt mit Koordinaten (17) (d.h. der Vektor (18) bzw. (19)) die gesamte Gerade.
Was wir damit gemacht haben, ist im Grunde nichts anderes, als die Gerade g
mit der Menge der reellen Zahlen zu identifizieren:
- Die Null (d.h. der Wert t = 0) entspricht
unserem Startpunkt (x0, y0).
- Die Eins (d.h. der Wert t = 1) entspricht dem Punkt mit Koordinaten
(x0 + ux, y0 + uy).
- Allgemein entspricht die reelle Zahl t
dem durch (17) definierten Punkt
(x(t), y(t)).
Eine solche Identifizierung nennen wir "Parametrisierung" der Geraden g.
Sehen Sie sich im nebenstehenden
Applet an, wie konkrete t-Werte
konkreten Punkten auf g entsprechen!
| | | |
Applet
Parameterdarstellung
von Geraden
| |
| | |
Diese Konstruktion ist für beliebige Geraden möglich (auch für solche, die
parallel zur y-Achse sind).
Bei der Wahl der beiden Zahlen ux und
uy, die ihre Richtung beschreiben, müssen wir
lediglich voraussetzen, dass sie nicht beide 0 sind,
und (x0, y0)
kann ein beliebiger Punkt auf der Gerade sein.
Daher ist die Parameterdarstellung einer Geraden mehrdeutig: Es gibt (unendlich) viele
Parameterdarstellungen derselben Geraden!
Die Zeit als Parameter
| | | |
| |
| | |
Wenn Sie sich unter einem Parameter, der "eine Gerade durchäuft", etwas möglichst Konkretes vorstellen wollen,
so denken Sie an die Zeit. Stellen Sie sich vor, eine kleine Perle laufe die Gerade entlang und ist zur Zeit
t an einem Punkt mit Koordinaten
(x(t), y(t)).
So ist sie etwa zur Zeit t = 0 an unserem
Startpunkt A.
Umgekehrt gibt es zu jedem Punkt der Geraden einen Zeitpunkt t,
zu dem unsere Perle gerade dort ist.
Die beiden Zahlen ux und
uy geben nicht nur an, in welche Richtung sich die Perle bewegt, sie
beschreiben auch, wie schnell sie das tut. Sie haben also etwas mit der Geschwindigkeit
der Perle zu tun.
Genauer ausgedrückt sind sie die Komponenten des Geschwindigkeitsvektors
u.
In genau dieser Weise wird in der Physik eine geradlinige und gleichförmige
(d.h. sich mit konstanter Geschwindigkeit vollziehende) Bewegung beschrieben.
Gerade durch zwei gegebene Punkte (Methode 2)
| | | |
| |
| | |
Nun können wir die oben versprochene zweite Methode, eine Gerade rechnerisch durch zwei vorgegebene Punkte
zu legen, besprechen: Sind zwei (verschiedene) Punkte P(x0, y0)
und Q(x1, y1)
gegeben, so gelangen wir, von P
ausgehend, nach Q, indem wir
- um
ux = x1 - x0 nach rechts und
- um
uy = y1 - y0 nach links
gehen.
Damit haben wir alles, was wir für eine Parameterdarstellung der gesuchten Geraden benötigen:
Einen Punkt auf der Geraden (wir wählen P)
und die beiden Zahlen
ux, uy,
die die Richtung der Geraden bestimmen.
Die Parameterdarstellung der Geraden durch
P und Q
lautet daher
x(t) = x0
+ t (x1 - x0) (x1 - x0)
y(t) = y0
+ t (y1 - y0) (y1 - y0)
|
|
|
(20) |
| | | |
| |
| | |
Formulierung mit Vektoren: Mit Hilfe der Vektorrechnung kann u
als Verbindungsvektor von P
nach Q berechnet werden:
u =
Q - P.
Er hat genau die Komponenten
(x1 - x0, y1 - y0),
wie sie auch in (20) auftreten.
Die Kurzschreibweise für die Parameterdarstellung (20) lautet daher
x(t)
= P + t (Q - P). (Q - P).
Sehen wir uns ein konkretes Beispiel an:
Beispiel: Man lege die Gerade durch die Punkte P(3, 4) und
Q(5, 1).
Lösung: Mit
ux = x1 - x0 = 5 - 3 = 2 und
uy = y1 - y0 = 1 - 4 = -3
ergibt sich sofort die gewünschte Parameterdarstellung:
x(t) = 3
+ 2 t t
y(t) = 4
- 3 t. t.
|
|
|
(21) |
Die rot und blau unterlegten Zahlen sollen Ihnen helfen,
das Zustandekommen des Resultats besser nachvollziehen zu können.
In der Formulierung mit Vektoren kann unmittelbar
Q - P = (5, 1) - (3, 4) = (2, -3)
berechnet und die Parameterdarstellung in der Form
x(t) = (3, 4) + t (2, -3)
oder
x(t) = (3 + 2 (2, -3)
oder
x(t) = (3 + 2 t, 4 -3 t, 4 -3 t)
angeschrieben werden t)
angeschrieben werden
Damit stehen Ihnen zwei Methoden zur Verfügung, eine durch zwei Punkte bestimmte Gerade zu beschreiben.
Sie sollten beide gut beherrschen, denn einerseits werden Sie sie beim Lösen von Aufgaben benötigen,
und andererseits stellen sie für sich genommen einen Test für das Verständnis der
Grundtatsachen der analytischen Geometrie dar.
Wechsel der Darstellung
| | | |

Verbindungsvektor
| |
| | |
Wir haben nun zwei Typen von Geradendarstellungen kennen gelernt: mit Hilfe von Geradengleichungen (explizit und implizit) und
mit Hilfe einer Parameterdarstellung. Sie können jederzeit, wenn es Ihnen sinnvoll
erscheint, die Darstellung wechseln.
Haben Sie eine Gerade in Parameterdarstellung vorliegen, so können Sie sie in Form einer
Geradengleichung darstellen, indem sie den Parameter eliminieren.
Um zu sehen, was das bedeutet, betrachten wir als Beispiel die durch
(21) gegebene Gerade.
Ist ein beliebiger Punkt (x, y)
gegeben, der auf ihr liegt, so entspricht ihm (genau) ein Parameterwert t,
d.h. es gibt dann eine Zahl t, für die
x = 3
+ 2 t t
y = 4
- 3 t t
|
|
|
|
gilt. Aus diesem System von Gleichungen kann t
eleminiert werden, z.B. indem beide Gleichungen nach t
aufgelöst
t = (x - 3)/2
t = (4 - y)/3
|
|
|
|
und die beiden rechten Seiten
gleichgesetzt werden. Damit ergibt sich (x - 3)/2 = (4 - y)/3
oder, etwas verschönert, 3x - 9 =
8 - 2y oder,
noch schöner angeschrieben,
Damit ist eine Darstellung durch eine implizite Geradengleichung vom Typ (11) gefunden.
Wird sie nach y aufgelöst,
so entsteht daraus die explizite Geradengleichung (9).
Haben Sie umgekehrt eine Gerade gegeben, die durch eine Gleichung dargestellt ist und benötigen eine
Parameterdarstellung, so wählen Sie zwei beliebige (voneinander verschiedene) Punkte der
Geraden und bestimmen mit der oben besprochenen Methode 2 eine Parameterdarstellung.
Ein Schnittproblem in Parameterdarstellung
| | | |
| |
| | |
Sie werden sich fragen, wozu die Parameterdarstellung der Gerade dient, wenn wir doch bereits
zwei andere Darstellungsformen durch Geradengleichungen zur Verfügung haben.
Der entscheidene Vorteil kommt vor allem dann
zum Tragen, wenn weiter unten Geraden im Raum betrachtet werden.
Im dritten Geometrie-Kapitel wird dieses Konzept dann verallgemeinert, um auch
gekrümmte Kurven (in Ebene und Raum) beschreiben zu können.
Die allgemeine Logik, wie eine Parameterdarstellung angewandt wird,
können wir uns aber auch bereits hier anhand eines Beispiels verdeutlichen:
Beispiel: Wo schneidet die durch (21) definierte Gerade g die
erste Mediane, d.h. jene Gerade, die durch die Gleichung
x = y
definiert ist, vgl. (1) oben.
Wir zeigen, wie diese Frage mit Hilfe der Parameterdarstellung beantwortet werden kann:
Da der gesuchte Punkt auf g
liegt, entspricht ihm genau ein Wert t des Parameters.
Da andererseits die Koordinaten jedes auf der ersten Mediane liegenden Punktes
x = y
erfüllen, muss das auch für den gesuchten Punkt gelten:
wobei x(t) und
y(t) die beiden in
(21) definierten Funktionen sind. Der entscheidende Punkt ist nun, dass das
eine Gleichung für t ist.
Können wir sie lösen, haben wir die Antwort auf die gestellte Frage.
Wir setzen ein und erhalten die Gleichung
3 + 2 t = 4 - 3 t = 4 - 3 t, t,
|
|
|
|
woraus sich die Lösung t = 1/5 ergibt.
Dieser Wert muss in (21) eingesetzt werden.
Der gesuchte Punkt hat daher die Koordinaten
(x(1/5), y(1/5)) =
(3 + 2/5, 4 - 3/5) =
(17/5, 17/5).
Obwohl dieses Beispiel sehr einfach ist (und auch mit anderen Methoden gelöst werden kann),
zeigt es den Grund für die Nützlichkeit der Parameterdarstellung auf:
|
Eine Bedingung an einen Punkt P der Geraden
(z.B. dass er auf der ersten Mediane liegt, wie im obigen Beispiel)
wird übersetzt in eine Bedingung an den Parameterwert t, der dem gesuchten Punkt
P entspricht (das war im obigen
Beispiel die Gleichung 3 + 2t = 4 - 3t).
Kann diese Bedingung an t gelöst werden
(im obigen Beispiel war die Lösung t = 1/5), so
ergibt sich P durch simples Einsetzen in die Parameterdarstellung.
|
|
|
Nachbemerkung: Eine Geradengleichung ist eine Gleichung in zwei Variablen
x und y.
Sie besitzt unendlich viele Lösungen. Geometrisch betrachtet entsprechen die Lösungen genau den
Punkten der Gerade. Algebraisch betrachtet ist die Parameterdarstellung die "allgemeine Lösung" der
Geradengleichung: Für jeden Wert von t, der
in sie eingesetzt wird, ergibt sich eine Lösung, und jede Lösung
kann auf diese Weise dargestellt werden.
Im nächsten Abschnitt werden wir die Idee der Parameterdarstellung
auf die Beschreibung von Geraden im (dreidimensionalen) Raum übertragen.
|
| | |

Analytische Geometrie 3
(in Vorbereitung)
| |
| | |
| Parameterdarstellung von Geraden im Raum |
| | | |
Zum Seitenanfang | |
| | |
Der Parameterdarstellung liegt eine mächtige und weitreichende Idee zugrunde.
Das zeigt sich sofort, wenn eine analytische (rechnerische) Darstellungsform für
Geraden im (dreidimensionalen) Raum gesucht wird.
Man könnte zunächst daran denken, eine Gerade im Raum (in Anagolie zum ebenen Fall) durch eine lineare Gleichung in drei Variablen
x, y
und z zu beschreiben. Allerdings beschreibt eine solche
Gleichung keine Gerade, sondern eine Ebene.
(So beschreibt etwa die Gleichung z = 0
die xy-Ebene).
Eine wenig attriaktive Möglichkeit bestünde darin, eine Gerade im Raum als
Schnitt zweier Ebenen zu beschreiben.
Es gibt eine bessere Lösung: die Parameterdarstellung. Sie ist die
einfachste und bequemste Form, Geraden im Raum zu beschreiben, und sie
kann ohne Probleme vom ebenen Fall auf den räumlichen Fall übertragen werden.
Wir können die Argumentation, die zu (17)
geführt hat, wortwörtlich übernehmen, wobei lediglich zur berücksichtigen ist,
dass eine Richtung im Raum durch drei Zahlen ux,
uy und uz
beschrieben werden kann, indem von einem beliebigen Punkt von aus
- um ux in die
x-Richtung,
- um uy in die
y-Richtung und
- um uz in die z-Richtung
| | | |

Beschreibung
von Ebenen
| |
| | |
gegangen wird.
(Mit dem nebenstehenden Applet können Sie Ihr Gefühl für räumliche Koordinaten
ein bisschen trainieren).
Die Parameterdarstellung einer Geraden g im Raum, deren Richtung durch
die drei Zahlen ux,
uy und uz
charakterisiert wird, und auf der der Punkt
A(x0, y0, z0)
liegt, lautet daher
x(t) = x0
+ t ux ux
y(t) = y0
+ t uy uy
z(t) = z0
+ t uz uz
|
|
|
(22) |
Für jeden Wert des Parameters t ergibt sich ein
Punkt auf g.
| | | |
Applet
Räumliche Koordinaten
| |
| | |
Formulierung mit Vektoren: Ebenso wie bei der Parameterdarstellung von Geraden in der Ebene, siehe (18) und (19),
kann auch hier die Vektorschreibweise verwendet werden. Die drei Beziehungen (22) heißen
dann
| |
⎛ |
x0 |
⎞ |
+ t |
⎛ |
ux |
⎞ |
, |
| x(t) = |
⎜ |
y0 |
⎟ |
⎜ |
uy |
⎟ |
| |
⎝ |
z0 |
⎠ |
⎝ |
uz |
⎠ |
|
(23) |
wobei x(t)
für (x(t), y(t), z(t))
steht, oder, in Kurzform,
mit
A = (x0, y0, z0)
und u = (ux, uy, uz).
u ist der
Richtungsvektor der Geraden g.
A ist der
Ortsvektor des gegebenen Punktes A, der auf der Geraden liegt.
Sehen wir uns eine konkrete Parameterdarstellung einer Geraden im Raum an:
| | | |
| |
| | |
Beispiel: Die Parameterdarstellung
x(t) = 4
+ 3 t t
y(t) = 3
-  t t
z(t) = 5
+ 2 t t
|
|
|
(25) |
beschreibt jene Gerade durch den Punkt (4, 3, 5),
deren Richtung durch die Zahlen
(3, -1, 2)
bestimmt ist. (25) kann auch in Vektorschreibweise
| |
⎛ |
4 |
⎞ |
+ t |
⎛ |
3 |
⎞ |
|
| x(t) = |
⎜ |
3 |
⎟ |
⎜ |
-1 |
⎟ |
| |
⎝ |
5 |
⎠ |
⎝ |
2 |
⎠ |
|
(26) |
angebeben werden.
Versuchen Sie, sich die Lage dieser Geraden gedanklich (z.B. unter Zuhilfenahme von Bleistiften) vorzustellen!
| | | |
| |
| | |
Als Übung versuchen Sie, Parameterdarstellungen der im nebenstehenden Applet
gezeigten Geraden im Raum zu finden!
Wie im Fall der Geraden in der Ebene ist auch die Parameterdarstellung einer Geraden im Raum
nicht eindeutig. Und auch hier können wir uns (wie bereits oben besprochen)
die Parameterdarstellung als Bewegung einer die Gerade entlang laufenden kleinen Perle
vorstellen. Der Parameter spielt dann wieder die Rolle der Zeit: Zur Zeit
t sind die Koordinaten der Perle
durch
(x(t), y(t), z(t))
gegeben. Die Größen ux,
uy und uz
sind wieder die Komponenten des Geschwindigkeitsvektors
u.
Die einfachste Aufgabenstellung, bei der die Parameterdarstellung hilft, ist
das Auffinden einer Geraden durch zwei gegebene Punkte. Sie wird völlig analog zum
oben besprochenen ebenen Fall (Methode 2) gelöst. Der einzige Unterschied besteht darin, dass sich zu den zwei
ebenen jetzt eine dritte Koordinate hinzugesellt. Die Gerade durch die Punkte
P(x0, y0, z0)
und Q(x1, y1, z1)
ist, in Verallgemeinerung von (20), durch
x(t) = x0
+ t (x1 - x0) (x1 - x0)
y(t) = y0
+ t (y1 - y0) (y1 - y0)
z(t) = z0
+ t (z1 - z0) (z1 - z0)
|
|
|
(27) |
gegeben. Die entsprechende Kurzschreibweise mit Vektoren lautet
x(t)
= P + t (Q - P). (Q - P).
Um Ihnen ein Gefühl dafür zu geben, was man mit der Parameterdarstellung einer Geraden im
Raum sonst noch anstellen kann, betrachten wir ein kleines Beispiel:
| | | |
Applet
Geraden im Raum bestimmen
| |
| | |
Beispiel: Wo schneidet die durch (25) bzw. (26) definierte Gerade g die
xy-Ebene?
Um diese Frage rechnerisch zu lösen, bedenken wir, dass
(25) für jeden Wert von t
die Koordinaten eines Punktes auf der Geraden ergibt. Daher formulieren wir unsere Frage so:
Für welches t liegt der durch
(25) gegebene Punkt
(x(t), y(t), z(t))
in der xy-Ebene?
Das ist genau dann der Fall, wenn seine z-Koordinate
gleich 0, d.h. wenn
z(t) = 0 ist.
Was wir über den gesuchten Schnittpunkt wissen, kann daher in Form der Gleichung
5 + 2 t = 0
ausgedrückt werden. Wir lösen sie nach t auf
und erhalten t = -5/2.
Das ist der gesuchte Wert des Parameters.
Um die Koordinaten des Schnittpunkts von g mit der
xy-Ebene zu berechnen, brauchen wir nur noch
t = -5/2
in (25) einzusetzen und erhalten als Lösung der gestellten Aufgabe
(-7/2, 11/2, 0). t = 0
ausgedrückt werden. Wir lösen sie nach t auf
und erhalten t = -5/2.
Das ist der gesuchte Wert des Parameters.
Um die Koordinaten des Schnittpunkts von g mit der
xy-Ebene zu berechnen, brauchen wir nur noch
t = -5/2
in (25) einzusetzen und erhalten als Lösung der gestellten Aufgabe
(-7/2, 11/2, 0).
Nachbemerkung: Dass die letzte Komponente 0 ist, ist natürlich kein Zufall, sondern
eine Bestätigung, dass der gefundene Punkt tatsächlich in der xy-Ebene liegt,
d.h. dass wir die Gleichung 5 + 2 t = 0
korrekt gelöst haben. t = 0
korrekt gelöst haben.
Hier begegnen wir wieder der Logik, die wir schon oben im ebenen Fall besprochen haben: Eine Bedingung
an einen Punkt P der Geraden
wird übersetzt in eine Bedingung an den Parameterwert t
(in der Regel eine Gleichung).
Wir werden die Parameterdarstellung von Geraden im Raum im zweiten Geometrie-Kapitel dazu benutzen,
um Lagebeziehungen von Geraden mit Ebenen und von Geraden untereinander
zu untersuchen und die dabei auftretenden Schnittpunkte zu berechnen.
|
| | |

Lagebeziehungen von Ebenen und Geraden
| |
| | |
| Lagebeziehungen von Geraden in der Ebene |
| | | |
Zum Seitenanfang | |
| | |
Wir kehren nun für den Rest dieses Kapitels in die zweidimensionale Welt der Zeichenebene zurück.
Zwei Geraden der Zeichenebene können in die gleiche Richtung verlaufen oder in verschiedene Richtungen,
d.h. die können zueinander parallel sein oder nicht. Das sind die beiden
grundlegenden Fälle, die auftreten können, wenn zwei gegebene Geraden
g und g'
auf ihre Lagebeziehung geprüft
werden sollen. Wir nehmen nun an, dass jede der Geraden in einer der Formen
- explizite Geradengleichung (9)
- implizite Geradengleichung (11)
- Parameterdarstellung (17) bzw. (18) oder in der Kurzform (19)
gegeben ist und besprechen, wie Sie beim Vergleich zweier Geraden vorgehen können.
Dabei beschränken wir uns auf Methoden, für die keine Vektorrechnung
nötig ist und werden im zweiten Geometrie-Kapitel noch einige Techniken hinzufügen.
In konkreten Berechnungen können Sie, wie oben besprochen, die Darstellungsform einer Geraden jederzeit wechseln, wenn es Ihnen
vorteilhaft erscheint.
| | | |

Lagebeziehungen von Geraden in der Ebene
| |
| | |
- Feststellen, ob g und g'
zueinander parallel sind:
Dazu erinnern wir uns, dass die Richtung einer Geraden
- in der expliziten Geradengleichung
durch den Anstieg k,
- in der impliziten Geradengleichung durch die beiden Konstanten a,
b (die Komponenten des Normalvektors)
- und in der Parameterdarstellung durch die beiden Zahlen
ux, uy
(die Komponenten des Richtungsvektors)
festgelegt ist. Um festzustellen, ob g und g'
parallel sind, gibt es mehrere Methoden. Eine besteht darin, zu überprüfen
- ob beide Geraden zur y-Achse parallel sind oder
- ob sie die gleichen Anstiege besitzen.
Der Anstieg einer (nicht zur y-Achse parallelen
Geraden) kann mit Hilfe der Formeln (12) für die implizite Geradengleichung und (15) für die
Parameterdarstellung berechnet werden.
- Falls g und g'
zueinander parallel sind:
Es können nun zwei Fälle auftreten: Entweder die beiden Geraden sind identisch oder sie sind verschieden.
Um zu entscheiden, welcher Fall zutrifft, kann folgende (intuitiv einleuchtende) Tatsache benutzt werden:
Zwei parallele Geraden in der Zeichenebene sind genau dann identisch, wenn sie einen gemeinsamen Punkt besitzen.
Wie ein gemeinsamer Punkt zweier Geraden gefunden werden kann, besprechen wir ein paar Zeilen weiter
unten.
- Falls g und g'
nicht zueinander parallel sind:
Zwei Geraden in der Zeichenebene, die nicht zueinander parallel sind, haben genau einen gemeinsamen Punkt (wir nennen ihn ihren
Schnittpunkt).
Wenn Sie diese Liste gelesen haben, wird Ihnen vielleicht aufgefallen sein, dass das Problem der Lagebeziehung
zweier Geraden in der Zeichenebene auf die
Ermittlung ihrer Schnittmenge (d.h. der Menge aller Punkte, die auf beiden
Geraden liegen) zurückgeführt werden kann:
- Gibt es keinen Schnittpunkt, so sind g und g'
zueinander parallel und nicht identisch.
- Gibt es mehr als einen Schnittpunkt, so sind g und g'
identisch. (In diesem Fall gibt es unendlich viele Schnittpunkte).
- Gibt es genau einen Schnittpunkt, so sind g und g'
nicht zueinander parallel.
Damit ergibt sich eine andere Möglichkeit, die Lagebeziehung von zweier Geraden zu analysieren.
Statt nach der obigen Liste vorzugehen (d.h. die Lagebeziehungen der Geraden aus den in ihren Darstellungen
enthaltenen geometrischen Informationen zu bestimmen), können Sie einfach "stur"
rechnerisch ihre Schnittmengen ermitteln und erhalten dabei ganz automatisch die gesuchte
Information über die Lagebeziehung.
Schnittmengen von Geraden in der Ebene
| | | |
| |
| | |
Schnittmengen von Geraden in der Zeichenebene können auf verschiedene Weisen berechnet werden, je nachdem,
in welchen Darstellungsformen sie gegeben sind oder wie es bequem erscheint:
- Sind unsere beiden Geraden g und g'
durch eine (implizite oder explizite) Geradengleichung gegeben, so ist jede von ihnen
die Lösungsmenge einer Gleichung in zwei Variablen
x und y.
Ein gemeinsamer Punkt (x, y)
der beiden Geraden muss daher beide Gleichungen erfüllen.
Mit anderen Worten: Die beiden Geradengleichungen müssen gemeinsam als (lineares) Gleichungssystem
(zwei Gleichungen in zwei Variablen)
aufgefasst werden.
Die drei Lösungsfälle entsprechen genau den drei möglichen Lagebeziehungen:
- Die Lösungsmenge ist leer (d.h. die beiden Gleichungen widersprechen einander): Die Geraden
sind zueinander parallel und nicht identisch.
- Es gibt unendlich viele Lösungen: Die Geraden sind identisch.
- Es gibt genau eine Lösung: Die Geraden sind nicht zueinander parallel und schneiden einander daher
in (genau) einem Punkt.
Wir illustrieren diese drei Fälle anhand von drei Beispielen:
Beispiel 1: Die Lagebeziehung der Geraden
g: 3x + 2y = 2 und
h: 6x + 4y = 1
ist zu klären.
Ein Lösungsweg: Die beiden Gleichungen werden als ein Gleichungssystem
für die beiden Variablen x
und y aufgefasst.
Aus der ersten Gleichung ergibt sich
y = -3x/2 + 1.
Dies wird in die zweite Gleichung eingesetzt. Damit erhalten wir die Gleichung
6x - 6x + 4 = 1,
also einen Widerspruch. Daher existiert kein Schnittpunkt. Die beiden Geraden sind zueinander parallel und nicht identisch.
Ein anderer Lösungsweg: Wenn wir die Koeffizienten auf den linken Seiten der Geradengleichungen
betrachen, so fällt uns auf, dass jene der zweiten Gleichung doppelt so groß sind wie
jene der ersten Gleichung.
Indem wir die erste Gleichung mit 2 multiplizieren,
erhalten wir g: 6x + 4y = 4.
Die beiden (neuen) Geradengleichungen haben nun die gleichen Koeffizienten
a, b,
daher die gleiche Richtung. Sie sind zueinander parallel. Sie sind aber nicht identisch, da die rechten
Seiten verschieden sind. Wir brauchen die Gleichungen nur voneinander subtrahieren, um den
Widerspruch 0 = 3 zu erhalten.
Beispiel 2: Die Lagebeziehung der Geraden
g: 3x + 2y = 2 und
h: 6x + 4y = 4
ist zu klären.
Ein Lösungsweg: Die beiden Gleichungen werden als ein Gleichungssystem
für die beiden Variablen x
und y aufgefasst.
Aus der ersten Gleichung ergibt sich
y = -3x/2 + 1.
Dies wird in die zweite Gleichung eingesetzt. Damit erhalten wir die Gleichung
6x - 6x + 4 = 4,
also eine Aussage, die für alle x wahr ist.
Es gibt unendlich viele Schnittpunkte (zu jedem x ist
die zugehörige y-Koordinate durch
y = -3x/2 + 1
gegeben). Die beiden Geraden sind identisch.
Ein anderer Lösungsweg: Wenn wir die Koeffizienten auf den linken Seiten der Geradengleichungen
betrachen, so fällt uns auf, dass jene der zweiten Gleichung doppelt so groß sind wie
jene der ersten Gleichung.
Indem wir die erste Gleichung mit 2 multiplizieren,
erhalten wir g: 6x + 4y = 4.
Die beiden (neuen) Geradengleichungen sind nun identisch, und daher sind auch die Geraden, die sie beschreiben,
identisch.
Beispiel 3: Die Lagebeziehung der Geraden
g: 3x + 2y = 2 und
h: x + 4y = 1
ist zu klären. Falls ein Schnittpunkt existiert, sind seine Koordinaten zu berechnen.
Lösungsweg: Die beiden Gleichungen werden als ein Gleichungssystem
für die beiden Variablen x
und y aufgefasst.
Aus der ersten Gleichung ergibt sich
y = -3x/2 + 1.
Dies wird in die zweite Gleichung eingesetzt. Damit erhalten wir die Gleichung
x - 6x + 4 = 1,
deren einzige Lösung
x = 3/5
ist.
Es gibt also genau einen Schnittpunkt, dessen x-Koordinate
gleich 3/5 ist.
Seine y-Koordinate
ist durch
y = -9/10 + 1 = 1/10
gegeben.
- Sind beide Geraden in der Parameterdarstellung gegeben, so ergibt sich ebenfalls ein (lineares) Gleichungssystem,
diesmal aber für die Parameter. Wir illustrieren das anhand eines Beispiels:
Beispiel: Die Gerade g ist durch
x(t) = 3
+ 2 t t
y(t) = 4
- 3 t t
|
|
|
(28) |
und die Gerade h ist durch
x(t) = 3
+ 5 t t
y(t) = 2
- 7 t t
|
|
|
(29) |
gegeben. Ihr Schnittpunkt ist zu ermitteln. Hierbei ist zunächst etwas Wichtiges zu beachten:
Die Parameter sind hier für beide Geraden mit t
bezeichnet (genauso, wie bei der Definition zweier Funktionen beide Male die Variable
x genannt werden kann).
Tatsächlich aber müssen die Parameterwerte des Schnittpunkts nicht für beide
Geraden gleich sein. Daher ist es günstiger, von Beginn an für den Parameter der Geraden
h ein anderes Symbol zu verwenden,
z.B. sie anstelle von (29) durch eine simple Umbenennung in die Form
x(s) = 3
+ 5 s s
y(s) = 2
- 7 s s
|
|
|
(30) |
umzuschreiben. Dem Schnittpunkt entspricht nun ein Wert für t
(da er auf g liegt)
und ein Wert für s
(da er auf h liegt).
Seine x-Koordinate ist
3 + 2 t und gleichzeitig
3 + 5 t und gleichzeitig
3 + 5 s.
Seine y-Koordinate ist
4 - 3 s.
Seine y-Koordinate ist
4 - 3 t und gleichzeitig
2 - 7 t und gleichzeitig
2 - 7 s.
Die beiden Parameterwerte erfüllen also das (lineare) Gleichungssystem s.
Die beiden Parameterwerte erfüllen also das (lineare) Gleichungssystem
3 + 2 t
= 3 + 5 t
= 3 + 5 s s
4 - 3 t
=
2 - 7 t
=
2 - 7 s. s. |
|
|
(31) |
Als Lösung dieses Gleichungssystems ergibt sich
t = 10 und
s = 4.
Die Koordinaten des Schnittpunkts können nun berechnet werden, indem
t = 10 in
(28) oder indem s = 4 in
(30) eingesetzt wird. (In beiden Fällen muss derselbe Punkt herauskommen,
was eine gute Gelegenheit für eine Probe ist). Wir erhalten als Koordinaten des
Schnittpunkts
(23, -26).
Ganz allgemein können bei dieser Methode, die Schnittmenge zweier Geraden zu ermitteln, die gleichen drei Lösungsfälle wie oben auftreten:
keine Lösung, unendlich viele Lösungen, eine Lösung.
| | | |

Gleichungssysteme
Lineare Gleichungssysteme
| |
| | |
- Ist eine Gerade durch eine (explizite oder implizite) Geradengleichung, die
andere in der Parameterdarstellung gegeben,
so führt das Schnittmengenproblem auf eine einzige (lineare) Gleichung für den Parameter.
Dazu müssen lediglich die Funktionen
x(t) und
y(t) der in Parameterdarstellung gegebenen Geraden
anstelle von x und y
in die Gleichung der anderen Geraden eingesetzt werden. Daraus ergibt sich eine (lineare) Gleichung für
t.
Wieder gibt es drei Lösungsfälle:
- Die Lösungsmenge ist leer (d.h. die lineare Gleichung führt auf einen Widerspruch): Die Geraden
sind zueinander parallel und nicht identisch.
- Es gibt unendlich viele Lösungen: Die Geraden sind identisch.
- Es gibt genau eine Lösung: Die Geraden sind nicht zueinander parallel und schneiden einander daher
in (genau) einem Punkt.
Ein Beispiel dafür haben wir schon weiter oben betrachtet, als wir
den Schnittpunkt der durch (21) definierten Geraden mit der ersten Mediane
berechnet haben.
| | | |

lineare Gleichungen
| |
| | |
Die enge Verbindung zwischen dem Schnittmengenproblem und den Lösungsfällen von Gleichungssystemen ist ein typischer Zug
der analytischen Geometrie. Sie hat zu einem Wechselspiel zwischen
den zwei mathematischen Teilgebieten Geometrie und Gleichungssysteme geführt:
Um Lagebeziehungen von Geraden zu analysieren und deren Schnittpunkte zu finden, werden lineare Gleichungssysteme
untersucht (wobei jede Gerade durch eine Gleichung in zwei Variablen dargestellt wird).
Umgekehrt kann ein lineares Gleichungssystem in zwei Variablen (die zunächst gar nichts mit Geometrie zu tun haben müssen)
geometrisch als eine Frage nach Lagebeziehung und Schnittmengen von Geraden gedeutet werden
(wobei jede auftretende Gleichung als Gleichung einer Geraden interpretiert wird).
Da lineare Gleichungen und Gleichungssysteme systematisch behandelt werden können, helfen uns elektronische
Tools verlässlich beim Lösen und Darstellen geometrischer Probleme. Ihnen
wenden wir uns nun noch kurz zu.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Ein besonderer Typ von Programmen ist eigens der Darstellung geometrischer Sachverhalte gewidmet. Sie
werden unter dem Namen dynamische Geometrie
zusammengefasst. Die meisten dieser Programme erlauben zwar geometrische Darstellungen
(im Sinne von Konstruktionen) auf eine sehr schöne interaktive Art, den so genannten "Zug-Modus".
Ihre Möglichkeiten, die rechnerische Seite der analytischen Geometrie zu unterstützen und darzustellen,
sind aber eher begrenzt. Eine Ausnahme bildet ein unter dem Namen
GeoGebra
von Markus Hohenwarter (Universität Salzburg) entwickeltes Programm.
Neben der traditionellen dynamisch-geometrischen Darstellung besitzt es ein "Algebra-Fenster", in dem
die Gleichungen der einzelnen Objekte (und Koordinaten der auftretenden Punkte)
angezeigt werden - ganz
im Sinne der analytischen Geometrie! Die Anzeigen von Konstanten und Koordinaten
erfolgen dabei allerdings numerisch (d.h. näherungsweise, nicht symbolisch).
GeoGebra kann Vektoren darstellen und enthält zudem zahlreiche Features, die über die Geometrie hinausgehen
(vom Plotten von Funktionsgraphen bis zum Differenzieren und Integrieren)
und kann gratis downgeloadet werden.
Weiters besitzen alle Computeralgebra-Systeme
Funktionalitäten, die in der analytischen Geometrie eingesetzt werden können
(insbesondere das Lösen von Gleichungssystemen). Um derartige Berechnungen online
durchzuführen, können Sie unser Tool
Online-Rechnen mit Mathematica
benutzen.
| | | |
| |
| | |
Um Geraden zu zeichnen, die nicht parallel zur y-Achse sind,
können Sie den
mathe online Funktions-Plotter
oder den
Excel-Plotter
benutzen.
All diese Tools helfen uns beim Rechnen und Zeichnen, und sie helfen uns sogar beim Verstehen des Zusammenspiels zwischen
geometrischen und algebraischen Strukturen.
Die stärksten Werkzeuge sind aber - gerade in der Geometrie -
die menschliche Vorstellungskraft und die Intuition, die Computerprogramme nun einmal nicht
haben.
|
| | |
| |