| | |
| | | |
| |
| | |
| | | |
| |
| | |
Gleichungssysteme treten – ebenso wie Gleichungen – in der Mathematik und ihren Anwendungen sehr oft auf.
Insbesondere die linearen Gleichungssysteme sind von überragender Wichtigkeit. Für einen
schnellen Einstieg in dieses Thema bieten wir Ihnen einen Exkurs an (siehe den Button rechts), der Ihnen einen ersten Überblick
verschaffen kann.
| | | |
Lineare Gleichungssysteme
| |
| | |
Wenn Sie an einer ausführlicheren Hinführung interessiert sind, die eine Besprechung zweier systematischer Lösungsverfahren und
die geometrische Interpretation ebenso mit einschließt wie einige Betrachtungen über nichtlineare Gleichungssysteme,
dann lesen Sie den nun folgenden Text!
Sehen Sie sich den Exkurs danach "zum Drüberstreuen" an! Er sollte Ihnen dann nichts Neues mehr sagen, sofern Sie
das Wesentliche verstanden haben.
|
| | |
| |
| | |
| Gleichungen und Gleichungssysteme |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Gleichungen in mehreren Variablen
Eine Gleichung ist die Behauptung, dass zwei Terme, die eine oder mehrere Variable enthalten, gleich sind.
Hier ein ganz einfaches Beispiel:
und hier ein anderes:
| | | |

Gleichungen
| |
| | |
Gleichung (1) ist eine Gleichung in einer Variablen,
Gleichung (2) ist eine Gleichung in zwei Variablen.
Eine Lösung der Gleichung (1) ist eine (reelle) Zahl
x,
die, in (1) eingesetzt, zu einer wahren Aussage führt.
Eine Lösung der Gleichung (2) ist ein (reelles) Zahlenpaar
(x, y),
das, in (2) eingesetzt, zu einer wahren Aussage führt.
Die Menge aller Lösungen einer Gleichung heißt deren Lösungsmenge.
Sehen wir uns die Lösungsmengen der beiden obigen Beispiele an:
- Die Lösungsmenge von (1) besteht aus den beiden Zahlen
–9/4 und
2. Wir können sie auch in der Form
L = {–9/4, 2}
anschreiben. Das Beispiel zeigt, dass eine Gleichung mehrere Lösungen besitzen kann.
Um zu überprüfen, dass die Zahlen –9/4 und
2 Lösungen sind, müssen Sie sie nur
in (1) einsetzen. In beiden Fällen erhalten Sie die wahre Aussage
18 = 18.
Um die gesamte Lösungsmenge einer Gleichung zu finden, müssen entsprechende Lösungstechniken
angewandt werden.
Da es sich bei (1) um eine quadratische Gleichung handelt, können
Sie die dazu im Gleichungskapitel besprochene Methode nutzen. Verifizieren Sie selbst, dass die Gleichung (1)
neben –9/4 und
2 keine weiteren Lösungen besitzt!
- Die Lösungsmenge von (2) besitzt unendlich viele Elemente:
- Eine Lösung ist durch das Zahlenpaar
(0, 4) gegeben.
Das bedeutet: Wird
x = 0 und
y = 4 in
(2) eingesetzt, so ergibt sich eine wahre Aussage. Verifizieren Sie das!
- Eine andere Lösung ist durch das Zahlenpaar
(1, 10/3) gegeben.
Verifizieren Sie das!
- Eine weitere Lösung ist durch das Zahlenpaar
(2, 8/3) gegeben.
Verifizieren Sie auch das!
- Um einzusehen, dass die Gleichung (2) tatsächlich unendlich viele Elemente
besitzt, können Sie den Wert von x
beliebig vorgeben. Sie erhalten dann eine Gleichung in der einen Variablen
y, die stets eine Lösung besitzt, d.h.
die Sie nach y auflösen können.
Auf diese Weise können Sie so viele Lösungen finden, wie sie wollen!
Sie können auch einen beliebigen Wert von y
vorgeben und nach x auflösen, wenn Ihnen das
lieber ist. Auch mit dieser Methode können Sie so viele Lösungen finden, wie sie wollen!
Aber auch kompliziertere Gleichungen in mehreren Variablen spielen in der Mathematik und ihren Anwendungen eine Rolle.
Eine besonders gefährlich aussehende Gleichung ist etwa
|
2x3 – xy2 = (7x + y3)4 – 1 .
|
|
|
(3) |
Auch wenn es nicht immer leicht ist, Lösungen solcher Gleichungen zu finden, sollte Ihnen im Prinzip klar sein,
was eine Lösung ist. Verifizieren Sie, dass das Zahlenpaar
(0, 1) eine Lösung von
(3) darstellt! Dazu müssen Sie nur
x = 0
und
y = 1
einsetzen und sich davon überzeugen, dass sich daraus eine wahre Aussage ergibt.
(Trauen Sie sich – es ist ganz leicht!)
| | | |

reelle Zahlen
Zahlenpaare

quadratische Gleichungen
| |
| | |
Lineare Gleichungen in mehreren Variablen
Eine wichtige Eigenschaft der Gleichung (2) besteht darin, dass sie linear ist. Wir können sie
in eine einfachere Form bringen, in dem wir zu beiden Seiten
2y
addieren. Wir erhalten dann
Jede lineare Gleichung kann in eine solche Form gebracht werden:
- Auf der linken Seite steht eine Summe von Termen der Form "vorgegebene Zahl mal Variable".
Die vorgegebenen Zahlen, die vor den
Variablen stehen, heißen Koeffizienten (oder Vorfaktoren). Der Koeffizient von
x ist in diesem Beispiel gleich 2,
der Koeffizient von
y ist 3.
Eine solche Summe (hier also
2x + 3y) nennen wir eine Linearkombination
der Variablen.
- Auf der rechten Seite steht eine vorgegebene Zahl (hier also
12), die ebenfalls manchmal als Koeffizient bezeichnet wird, obwohl sie nicht
als Vorfaktor einer Variable auftritt.
Die "vorgegebenen Zahlen" werden auch schlicht Konstanten genannt – weil sie eben vorgegeben und damit konstant sind.
Lineare Gleichungen können auch von einer einzigen Variable abhängen (lineare Gleichungen in einer Variablen
wurden bereits im Gleichungskapitel behandelt), und sie können von mehr als zwei Variablen abhängen.
Ganz allgemein kann eine lineare Gleichung in n
Variablen in der Form
| | | |

lineare Gleichungen
in einer Variablen
| |
| | |
|
a1x1 + a2x2 + ...
+ anxn
= c
|
|
|
(4) |
angeschrieben werden, wobei die Variablen nun mit
x1, x2, ... xn,
die zugehörigen Koeffizienten mit
a1, a2, ... an
und die Konstante auf der rechten Seite mit
c
bezeichnet werden. Ist c = 0, so nennen wir die Gleichung
homogen, ist c ≠ 0, so nennen wir sie
inhomogen.
Bemerkung: Wir wollen uns die Möglichkeit vorbehalten, dass in (4) manche der Koeffizienzen
a1, a2, ... an
gleich 0 sind, aber wir wollen immer
annehmen, dass zumindest einer ≠ 0
ist.
Falls nur wenige Variablen im Spiel sind, wird meist auf die Durchnummerierung verzichtet:
- Ist
n = 2, so werden die
Variablen oft
– wie auch wir es in unserem Beispiel (2) bzw. (2') getan haben –
mit den Buchstaben x und
y bezeichnet.
Es ist dann also
x1 mit x
und
x2 mit y
zu identifizieren.
- Ist
n = 3, so werden für die Variablen
oft die Buchstaben x,
y und z
gewählt.
Klarerweise können auch andere Symbole für die Variablen benutzt werden. Das ist insbesondere dann von Bedeutung, wenn sie in Anwendungen
für etwas Konkretes stehen, etwa r für den
Preis von 1 Liter roter Farbe und v für den
Preis von 1 Liter violetter Farbe. Falls Sie 3 Liter rote und 2 Liter violette Farbe benötigen, aus einer großen Auswahl
unterschiedlich teurer Farben wählen können und ihr Budget von 25 Euro ganz ausgeben wollen, so
müssen Sie sich für solche Farben entscheiden, deren Preise die Gleichung
erfüllen. (In diesem Fall müssten Sie – wenn Sie mathematisch ganz korrekt sein wollen – noch die Zusatzbedingung
stellen, dass r und
v positiv sind.)
Jede lineare Gleichung in mehr als einer Variablen besitzt (sofern nicht alle Koeffizienten gleich 0
sind) unendlich viele Lösungen. Es ist auch ganz klar, warum das so ist: Geben Sie die Werte aller Variablen bis
auf einer frei vor (wobei der Koeffizient dieser einen ≠ 0 sein muss)!
Damit erhalten Sie eine lineare Gleichung in einer einzigen Variablen, die Sie lösen können.
Da dieser Umstand sehr wichtig ist, verdeutlichen wir ihn anhand eines einfachen Beispiels.
Wir formulieren es zuerst in Worten: Die Summe zweier (reeller) Zahlen soll gleich
3 sein. Als Gleichung angeschrieben:
Eine Lösung dieser Gleichung ist durch die Angabe zweier
reeller Zahlen x und y
festgelegt, deren Summe 3 ist.
Geben Sie eine vor und berechnen sie daraus die andere – auf diese Weise erhalten Sie so viele Lösungen, wie sie
wollen.
- Etwa: Ist die erste Zahl (x) gleich 1,
so ist die zweite Zahl (y)
gleich 2.
- Oder:
Ist die erste Zahl (x) gleich π,
so ist die zweite Zahl (y)
gleich 3 – π.
- Ganz allgemein: Ist die erste Zahl (x) gleich t,
so ist die zweite Zahl (y)
gleich 3 – t. Wählen Sie eine beliebige
Zahl t, so erhalten Sie eine Lösung dieser Aufgabe!
Auf diese Weise können Sie jede Lösung der Gleichung (6) finden.
Lineare Gleichungen sind besonders einfach zu handhaben und in Anwendungen sehr wichtig.
Wir werden uns in einem Großteil dieses Kapitels auf Systeme von Gleichungen dieses Typs
konzentrieren.
| | | |
| |
| | |
Lineare Gleichungssysteme
Ein Gleichungssystem ist von der Idee her etwas sehr Einfaches: Es ist, wie der Name sagt, ein System mehrerer Gleichungen,
die alle für die gleichen Variablen formuliert sind (wobei die Zahl der Gleichungen und die Zahl der Variablen nicht
unbedingt übereinstimmen müssen, obwohl sie es in der Praxis oft tun).
Jede der Gleichungen des Systems besitzt ihre eigene Lösungsmenge.
Eine Lösung des Gleichungssystems ist eine gemeinsame Lösung aller dieser Gleichungen. Sie muss also
jede einzelne Gleichung des Systems erfüllen.
Sind alle Gleichungen eines Systems linear, so sprechen wir von einem linearen Gleichungssystem.
Betrachten wir als Beispiel das folgende (lineare) System von 2 Gleichungen in 2 Variablen:
Eine Lösung dieses Gleichungssystems ist ein (reelles) Zahlenpaar
(x, y),
das sowohl (7a) als auch (7b) erfüllt (also zu einer wahren Aussage macht).
Wir können dieses System auch in Worten formulieren: Die Summe zweier Zahlen sei gleich
3, ihre Differenz sei gleich
1. Mit ein bisschen Nachdenken (so wie Sie es bei
Denksportaufgaben machen) finden Sie sicher eine Lösung: Sie entspricht dem Zahlenpaar
(2, 1), also
x = 2 und
y = 1.
Wichtig ist, dass beide Angaben, also
"x = 2" und
"y = 1" gemeinsam eine
Lösung bezeichnen. Um das zu betonen, können wir sie auch in der Form
anschreiben.
| | | |
| |
| | |
Da jede Lösung eines Gleichungssystems alle Gleichungen erfüllt, folgt:
|
Die Lösungsmenge eines Gleichungssystems ist gleich der Durchschnittsmenge der
Lösungsmengen der einzelnen Gleichungen.
|
|
Machen Sie sich klar, warum hier nicht die Vereinigungsmenge, sondern die Durchschnittsmenge der einzelnen Lösungsmengen
zu bilden ist! Wenn Sie eine Gleichung als Bedingung an die Lösungen interpretieren, so bedeutet das:
Alle Bedingungen müssen gleichzeitig erfüllt sein!
Je mehr Gleichungen (Bedingungen) zu erfüllen sind, um so weniger Lösungen wird es in der Regel geben.
Jede der beiden Gleichungen (7a) und (7b) besitzt unendlich viele Lösungen.
Das aus beiden Gleichungen bestehende System besitzt aber nur eine einzige Lösung, nämlich (8).
Davon können Sie sich selbst ganz leicht überzeugen:
Wenn (7a) und (7b) beide erfüllt sind, so muss sich eine wahre Aussage ergeben, wenn
die linken und die rechten Seiten dieser beiden Gleichungen addiert werden. Das führt aber mit
|
(x + y) + (x – y) = 3 + 1 ,
|
|
|
(7d) |
also
unmittelbar zur Erkenntnis, dass x = 2
sein muss. Setzen wir x = 2 in
(7a) und (7b) ein, so erhalten wir
Beide Gleichungen besitzen nur eine Lösung, und in beiden Fällen ist es die gleiche,
nämlich y = 1. Damit ist gezeigt,
dass (8) die einzige Lösung des Gleichungssystems (7a) – (7b)
ist. Obwohl (7a) und (7b) also jeweils unendlich viele Lösungen besitzen,
gibt es nur eine einzige, die sie beide gemeinsam haben.
Lineare Gleichungssysteme haben nicht immer eine Lösung, wie das einfache Beispiel
| | | |

Durchschnittsmenge
| |
| | |
illustriert. Wie auch immer x
und y gewählt werden –
es ist nicht möglich, dass x + y
gleichzeitig 1 und
–1 ist! Daher ist die Lösungsmenge des
Gleichungssystems (10a) – (10b) leer.
Es kann auch geschehen, dass ein Gleichungssystem unendlich viele Lösungen besitzt. Beispiele dafür werden
wir in diesem Kapitel noch kennen lernen.
Damit haben wir die grundsätzlichen Begrifflichkeiten, um die es in diesem Kapitel geht, abgesteckt.
Wir haben sie anhand linearer Gleichungssysteme illustriert, aber sie sind im Prinzip auch für nichtlineare Gleichungssysteme
wie
gültig:
- Ein Gleichungssystem ist ein System von mehreren Gleichungen in mehreren Variablen.
(Spezialfall: Ein lineares Gleichungssystem ist ein Gleichungssystem, das aus linearen Gleichungen besteht).
Die Zahl der Gleichungen muss nicht unbedingt mit der Zahl der Variablen übereinstimmen (obwohl das
in den meisten Anwendungsaufgaben der Fall ist).
- Eine Lösung eines Gleichungssystems muss alle Gleichungen des Systems gleichzeitig erfüllen.
- Die Lösungsmenge eines Gleichungssystems ist die Durchschnittsmenge der
Lösungsmengen der einzelnen Gleichungen.
Wie viele Lösungen ein Gleichungssystem besitzt (bzw. ob es überhaupt welche besitzt) hängt sehr stark
von den einzelnen Gleichungen ab.
|
|
Wir wenden uns nun den linearen Gleichungssystemen zu und werden nach zwei rechentechnischen Lösungsverfahren auch eine
nützliche geometrische Darstellung der durch sie beschriebenen Situationen kennen lernen.
|
| | |

leere Menge
| |
| | |
| Lineare Gleichungssysteme rechnerisch lösen |
| | | |
Zum Seitenanfang | |
| | |
Beim rechnerischen Lösen von Gleichungen ist der Begriff der Äquivalenzumformung zentral.
Er bezeichnet eine Umformung einer Gleichung, die auf eine andere (in der Regel einfachere) Gleichung führt,
die die gleiche Lösungsmenge wie die ursprüngliche Gleichung besitzt (und daher zu dieser äquivalent
gennant wird). Die wichtigsten
Äquivalenzumformung bestehen darin,
- einen Term zu beiden Seiten einer Gleichung zu addieren,
- beide Seiten einer Gleichung mit einem Term, der stets ≠ 0
ist, zu multiplizieren oder
- beide Seiten einer Gleichung durch einem Term, der stets ≠ 0
ist, zu dividieren.
Der Forderung, dass die neue Gleichung die gleiche Lösungsmenge besitzt wie die ursprüngliche, wird
dadurch Rechnung getragen, dass jede solche Umformung umkehrbar ist, also rückgängig gemacht
werden kann.
Beim rechnerischen Lösen von Gleichungssystemen kann nach dem gleichen Prinzip vorgegangen werden.
Durch einzelne Umformungsschritte, die gewährleisten, dass die Lösungsmenge nicht verändert wird, wird
ein Gleichungssystem so lange vereinfacht, bis es uns mehr oder weniger direkt die gesuchte Lösungsmenge
offenbart. Klarerweise dürfen auf die einzelnen Gleichungen beliebige Äquivalenzumformungen
angewandt werden (denn sie ändern die Lösungsmenge der entsprechenden Gleichung ja nicht).
Das bedeutet: Jede Gleichung eines Systems darf jederzeit durch eine zu ihr äquivalente
Gleichung ersetzt werden.
Es sind aber auch zusätzliche Operationen erlaubt, die mehrere Gleichungen miteinander kombinieren:
| | | |

Äquivalenz-
umformungen
| |
| | |
- Es dürfen zwei Gleichungen des Systems zueinander addiert werden (was bedeutet,
dass die linken und die rechten Seiten der beiden Gleichungen addiert werden). Die so erhaltene neue Gleichung
kommt dann zum System dazu, während eine der beiden anderen, aus denen sie gewonnen wurde, weggelassen werden kann.
Beweis: Wenn Sie von der neuen Gleichung jene subtrahieren, die sie nicht weggelassen haben, so ergibt sich
genau die weggelassene! Sie können einen solchen Schritt also immer rückgängig machen. Die Lösungsmenge des neuen
Gleichungssystems stimmt mit jener des ursprünglichen Gleichungssystems überein.
- Wird diese Regel mit den oben aufgelisteten Äquivalenzumformungen für einzelne Gleichungen
kombiniert, so kann sie etwas allgemeiner
formuliert werden: Es darf eine Linearkombination zweier Gleichungen gebildet werden (wobei die dabei verwendeten
Vorfaktoren ≠ 0 sein müssen).
Beispiel:
"2 mal der ersten minus
3 mal der zweiten Gleichung".
Die so erhaltene neue Gleichung
kommt zum System dazu, während eine der beiden anderen, aus denen sie gewonnen wurde, weggelassen werden kann.
Auch ein solcher Schritt kann immer rückgängig gemacht werden.
- Eine Gleichung, die stets eine wahre Aussage darstellt (also eine Identität, wie beispielsweise
2x + y = 2x + y
oder
0 = 0),
kann weggelassen werden. (Da sie stets erfüllt ist, liefert sie keine Information über die Lösungen
des Systems).
- Von zwei Gleichungen, denen Sie sofort ansehen, dass sie die
gleiche Lösungsmenge besitzen, darf eine weggelassen werden (denn das Gleichungssystem besitzt mit ihr oder ohne sie
die gleiche Lösungsmenge).
- Falls im Zuge dieser Umformungen ein Widerspruch auftritt, also eine Gleichung, die nie
erfüllt sein kann (wie beispielsweise
x = x + 1, was ja zu
0 = 1 umgeformt werden kann), so
können Sie aufhören: Das Gleichungssystem besitzt dann überhaupt keine Lösung.
(Klar: Wenn unter der Annahme, das Gleichungssystem besitze eine Lösung, ein Widerspruch folgt, so ist die
Annahme falsch).
Wichtig bei diesen Äquivalenzumformungen für lineare Gleichungssysteme ist, stets im Auge zu behalten, dass Sie
damit immer das gesamte Gleichungssystem umformen. Die übersichtlichste Form, sie anzuwenden, besteht darin,
nach jedem Schritt immer alle noch im Spiel befindlichen Gleichungen anzuschreiben. Da das eine gewisse
Schreibarbeit bedeutet, wird es nicht immer durchgehalten, aber zumindest am Anfang kann es Ihnen helfen,
den Überblick zu behalten und immer zu wissen, was Sie mit Ihren Umformungsschritten eigentlich
erreicht haben.
Generell können bei linearen Gleichungssystemen drei Lösungsfälle auftreten:
- Es gibt genau eine Lösung. Um mögliche Rechenfehler aufzuspüren,
machen Sie die Probe, indem Sie sie in alle Gleichungen des Systems einsetzen!
- Es gibt unendlich viele Lösungen. Wie eine Lösungsmenge mit unendlich vielen Elementen
beschrieben werden kann, werden wir noch besprechen.
- Es gibt keine Lösung.
Aufbauend auf diesen Regeln können Sie zwei Wege einschlagen, um eine lineares Gleichungssystem systematisch
zu vereinfachen.
| | | |

Identitäten
| |
| | |
Eliminationsverfahren
Das Eliminationsverfahren besteht darin, das System so zu vereinfachen, dass möglichst viele Gleichungen von
möglichst wenigen Variablen abhängen. (Variable werden – so gut es geht – aus den Gleichungen eliminiert).
Betrachten wir ein Beispiel:
Multiplizieren wir beide Seiten der ersten Gleichung mit –2
und beide Seiten der zweiten Gleichung mit 3, so ergibt sich als
neues Gleichungssystem
Anhand der rot dargestellten Terme können Sie den Zweck der Übung erkennen: Wenn Sie die
beiden Gleichungen addieren, fällt die Variable y
heraus (sie ist eliminiert)! Die Summe der beiden Gleichungen lautet
was zu
äquivalent ist. Um nun ganz genau vorzugehen: Gleichung (12f) kommt zum Gleichungssystem dazu, während
eine der beiden Gleichungen (12c) oder (12d) weggelassen werden kann. Wir werfen
(12d) weg, womit das vereinfachte Gleichungssystem (das aber die gleiche Lösungsmenge wie das ursprüngliche
besitzt)
lautet. Wir können nun das Eliminationsverfahren ein zweites Mal anwenden. Wir machen es diesmal etwas eleganter als vorhin
und bilden (in einem Schritt) die Summe "erste Gleichung plus 4 mal der zweiten",
was sofort auf
–6y = –6 und daher auf
y = 1
führt.
Wir lassen die erste der alten Gleichungen weg, womit sich das Gleichungssystem auf die Form
vereinfacht. Es besitzt die gleiche Lösungsmenge wie das ursprüngliche System
(12a) – (12b), aber in dieser Form sagt es uns direkt, dass die
einzige Lösung (x = –1, y = 1)
ist! Damit ist die Lösungsmenge gefunden. (In der Praxis hätte man, bei
(12g) – (12h) angelangt,
einfacher vorgehen können: Indem x = –1
in (12g) eingesetzt und nach y
aufgelöst wird, ergibt sich sofort y = 1).
Wie gestaltet sich der Ablauf dieser Methode für ein Gleichungssystem, das unendlich viele Lösungen besitzt?
Sehen wir uns das anhand des Beispiels
an. Wir bilden die Summe "–2 mal der ersten Gleichung plus
die zweite Gleichung" (um die Variable x zu eliminieren) und
erhalten die Gleichung
Diese dürfen wir ignorieren, womit das vereinfachte Gleichungssystem – nachdem (13b)
weggeworfen wird – lediglich aus Gleichung (13a) besteht! Was bedeutet das?
Es bedeutet, dass das gegebene Gleichungssystem unendlich viele Lösungen besitzt, nämlich alle Lösungen von
(13a)! Wir können einer der beiden Variablen einen beliebigen Wert zuweisen und
den Wert der anderen daraus berechnen: Wenn wir x
vorgeben, ergibt sich y = (1 – 2x)/3.
Die allgemeine Lösung kann daher in der Form
angeschrieben werden. Jede Lösung des Gleichungssystems (13a) – (13b)
kann auf diese Weise erhalten werden. Was hier passiert ist, ist logisch betrachtet einfach zu erklären: Die beiden
Gleichungen (13a) und (13b) des gegebenen Systems sind zueinander äquivalent – sie stellen die
gleiche Bedingung an die Lösung dar.
Um auch den letzten Lösungsfall, der eintreten kann, anhand eines Beispiels durchzuspielen,
betrachten wir das Gleichungssystem
an. Wir bilden die Summe "–2 mal der ersten Gleichung plus
die zweite Gleichung" (um die Variable x zu eliminieren)
und erhalten die Gleichung
also einen Widerspruch. Das Gleichungssystem (15a) – (15b) besitzt
keine Lösung. Seine Lösungsmenge ist leer.
Das Verfahren der schrittweisen Elimination kann auch im Fall von mehr als zwei Variablen angewandt werden.
Falls es eine eindeutig bestimmte Lösung gibt, läuft es ganz analog ab wie im Fall von zwei Variablen, nur sind mehr
Schritte nötig, um ans Ziel zu gelangen. Ist die Lösungsmenge leer, so wird dies daran erkannt, dass ein Widerspruch auftritt.
Falls es unendlich viele Lösungen gibt, so können mehrere Fälle eintreten. Für ein Gleichungssystem in
drei Variablen kann das vereinfachte System aus einer oder aus zwei Gleichungen bestehen:
- Besteht es aus einer einzigen Gleichung, so können zwei Variablenwerte frei
vorgegeben und der dritte daraus bestimmt werden.
- Besteht es aus zwei Gleichungen, so kann ein Variablenwert frei
vorgegeben werden, wodurch die Werte der beiden anderen Variablen festgelegt sind.
Betrachten wir zwei Beispiele:
Falls das vereinfachte Gleichungssystem lediglich aus der einzigen Gleichung
besteht, so ist die allgemeine Lösung durch
gegeben. Alternativ dazu könnten auch (x, z)
oder (y, z) frei vorgegeben werden.
Falls das vereinfachte Gleichungssystem aus den beiden Gleichungen
besteht, so führt der Versuch, x zu eliminieren,
wieder auf eine Gleichung, die zwei Variable enthält. Das Eliminationsverfahren liefert also
keine wirkliche Vereinfachung mehr. Der Grund dafür liegt in der Struktur der beiden Gleichungen:
Wird x vorgegeben, so können sie
sofort nach y
und z aufgelöst werden. Das zeigt, dass
es unendlich viele Lösungen gibt. Die allgemeine Lösung ist durch
gegeben. Alternativ dazu könnte auch der Wert von y
oder z frei vorgegeben werden.
| | | |
| |
| | |
Substitutionsverfahren
Wir erläutern diese Methode zuerst allgemein anhand eines Systems von drei linearen Gleichunge in drei Variablen
x,
y und
z.
Die drei Gleichungen wollen wir mit (I), (II) und (III) bezeichnen.
Der Ablauf sieht folgendermaßen aus:
- Sie beginnen damit, eine der Gleichungen – sagen wir (I) – nach einer Variablen – sagen wir x –
aufzulösen. Sie erhalten damit eine Gleichung (I'), die x
direkt durch y und z
ausdrückt, und die zu (I) äquivalent ist.
- Den erhaltenen Ausdruck für x benutzen Sie, um x
in den Gleichungen (II) und (III) durch
y und z
auszudrücken (d.h. Sie ersetzen – substituieren –
x durch den entsprechenden Ausdruck in
y und z).
Dadurch entstehen zwei neue Gleichungen (II') und (III'), die jetzt nur mehr
y und z
als Variable enthalten und zusammen mit (I') ein zum ursprünglichen äquivalentes Gleichungssystem darstellen.
- Mit (II') und (III') versuchen Sie, das Gleiche zu machen wie zuvor, also etwa (II') nach
y aufzulösen.
Falls das klappt, erhalten Sie eine Gleichung (II''), die y
unmittelbar durch z ausdrückt.
- Den erhaltenen Ausdruck für y setzen Sie in die verbleibende Gleichung (III') ein, wodurch eine neue Gleichung
(III'') entsteht, die nur mehr von
z abhängt.
- Im einfachsten Fall können Sie (III'') nach z lösen.
Dann sind sie praktisch fertig: Sie setzen den gefundenen Wert in (II'') ein, was
y bestimmt.
Die Werte für y und z
setzen Sie in (I') ein, womit
auch x bestimmt ist – damit ist die Lösung gefunden.
So einfach geht es aber nur, wenn das System nur eine einzige Lösung besitzt.
- Ergibt das Verfahren an irgendeinem Punkt eine Identität,
so gibt es unendlich viele Lösungen.
- Führt es auf einen Widerspruch, so gibt es gar keine Lösung.
Die Variablen, nach denen aufgelöst wird, und die Gleichungen, mit denen Sie das tun, können natürlich auch in
einer anderen Reihenfolge gewählt werden.
Betrachten wir ein Beispiel. Wir kennzeichnen die Gleichungen mit den in der allgemeinen Beschreibung verwendeten Symbolen:
Wir lösen (I) nach x
auf
und setzen (I') in (II) und
(III) ein. Das ergibt
Wir lösen (II') nach y
auf
und setzen (II'') in
(III') ein:
Dies ergibt sofort z = 5/7, was mit
(II'') auf y = 3/7
und mit (I') auf
x = 3/7
führt. Damit ist die (einzige) Lösung gefunden.
Wie ändert sich dieser Ablauf bei einem Gleichungssystem, das unendlich viele Lösungen besitzt? Auch dazu ein Beispiel:
Wir lösen (I) nach x
auf
und setzen (I') in (II) und
(III) ein:
Wir lösen (II') nach y
auf
und setzen (II'') in
(III') ein:
Hier tritt eine Identität auf, die ignoriert werden kann. Unser Gleichungssystem besteht demnach nur aus den
Gleichungen (I') und (II''). Die Form dieser beiden Gleichungen sagt uns
sofort, dass z beliebig vorgegeben werden kann.
Gleichung (II'') bestimmt dann den Wert von
y, und mit diesem schließen wir
aus (I'), dass
x = 1 – 3y + z = 1 – 4z/5 gilt.
Wir können die allgemeine Lösung daher in der Form
schreiben.
Für den dritten Lösungsfall brauchen wir kein eigenes Beispiel:
Tritt an irgendeinem Punkt des Ablaufs – etwa anstelle von (21h) – ein Widerspruch auf,
so hat das betreffende Gleichungssystem keine Lösung.
Ob Sie ein konkretes Gleichungssystem nun eher mit dem Eliminationsverfahren oder mit dem Substitutionsverfahren angehen
sollen, bleibt Ihnen überlassen. In den meisten Fällen ist es eine Frage des persönlichen Geschmacks. In manchen Fällen bietet
sich eines der beiden Verfahren als das kürzere und elegantere an. Mit ein bisschen Übung in beiden Methoden werden Sie selbst ein
Gefühl dafür entwickeln.
Grundsätzlich können beide Verfahren auch beim Lösen nichtlinearer Gleichungssysteme probiert werden,
wobei es allerdings keine Erfolgsgarantie gibt.
| | | |
| |
| | |
Ein bisschen Theorie zu Lösbarkeit und Lösungsmenge
Dieser Unter-Abschnitt kann von
''EinsteigerInnen'' ausgelassen werden.
Wir wollen nun ein paar allgemeine theoretische Resultate zu linearen Gleichungssystemen zusammenstellen.
Dabei werden wir – ausnahmsweise – eine Reihe von Begriffen erwähnen, die in späteren Kapiteln behandelt
werden, und die Sie vielleicht noch nicht kennen. Falls Sie an theoretischen Betrachtungen
über Gleichungssysteme weniger interessiert sind und diese nicht benötigen, so können Sie die folgenden
Absätze einfach überspringen. Falls nötig, kehren Sie bei Bedarf zu einem späteren Zeitpunkt zu ihnen
zurück.
Wir haben bereits weiter oben mit (4) eine Form angegeben, in die eine lineare Gleichung
in n Variablen stets gebracht werden kann.
Ein Gleichungssystem von m solchen Gleichungen
kann daher immer in die Form
|
a11x1 + a12x2 + ...
+ a1nxn
= c1
|
|
|
(23a) |
|
a21x1 + a22x2 + ...
+ a2nxn
= c1
|
|
|
(23b) |
|
. . . . . . . . . . . . . . . . . .
|
|
|
|
|
am1x1 + am2x2 + ...
+ amnxn
= cm
|
|
|
(23c) |
| | | |
| |
| | |
gebracht werden. Die mn Koeffizienten auf den linken Seiten der Gleichungen
(die a's) bilden gemeinsam eine Matrix,
d.h. ein rechteckiges Zahlenschema.
Die m Konstanten auf den rechten Seiten
(die c's)
können gemeinsam als Vektor mit m Komponenten
aufgefasst werden, den wir mit
c bezeichnen. Die Lösungsmenge hängt nur von diesen insgesamt
m (n + 1)
vorgegebenen Zahlen ab. Die Variablen
x1,
x2, ...
xm
fassen wir als einen Vektor mit n
Komponenten zusammen, den wir mit
x bezeichnen. Eine Lösung des Gleichungssystems
kann daher als ein Vektor x
angesehen werden, dessen Komponenten die Gleichungen (23) erfüllen.
Wie im ersten Vektorkapitel beschrieben, können Vektoren mit Zahlen multipliziert und
zueinander addiert werden – mit einem Wort: Wir können beliebige Linearkombinationen von Vektoren bilden.
Das werden wir im Folgenden benötigen.
Wir nennen nun ein lineares Gleichungssystem, das in die Form (23) gebracht wurde, homogen, wenn
c = 0 gilt, d.h. wenn
alle Konstanten auf den rechten Seiten
(die c's)
gleich 0 sind. Anderenfalls nennen es inhomogen – das ist der
Fall, wenn zumindest eine dieser Konstanten ≠ 0 ist.
(Wir schreiben dann c ≠ 0).
Haben wir ein inhomogenes lineares Gleichungssystem vor uns, so erhalten wir das zu ihm gehörende homogene
Gleichungssystem, indem wir
c = 0 setzen
und die a's unverändert lassen.
Mit diesen Begriffen lassen sich einige allgemeine Aussagen über die Lösungsmenge formulieren, die wir hier ohne Beweis
wiedergeben:
| | | |

Matrizen

Vektoren 1
| |
| | |
- Ein lineares Gleichungssystem ist genau dann homogen, wenn es die triviale Lösung
x = 0
(also x1 = x2 = ... = xn = 0)
besitzt.
- Ein homogenes lineares Gleichungssystem besitzt entweder nur eine einzige Lösung (nämlich die triviale) oder unendlich viele
Lösungen.
- Die Lösungsmenge eines homogenen linearen Gleichungssystem hat die Eigenschaft, dass
jede Linearkombination von Lösungen wieder eine Lösung ist.
Stellt also der Vektor
x eine Lösung des Gleichungssystems dar, und stellt der Vektor
x' eine andere Lösung des Gleichungssystems dar, und
sind r und
s beliebige reelle Zahlen, so stellt der Vektor
ebenfalls eine Lösung des Gleichungssystems dar. Insbesondere ist jedes Vielfache einer Lösung und jede Summe
von Lösungen wieder eine Lösung. Diese Eigenschaft macht die Lösungsmenge jedes homogenen
linearen Gleichungssystems zu einem Vektorraum (ein Konzept, das in der linearen Algebra
eine wichtige Rolle spielt).
- Ein inhomogenes lineares Gleichungssystem besitzt
- entweder eine einzige Lösung
- oder unendlich viele Lösungen
- oder keine Lösung.
Das sind die drei grundsätzlich möglichen Lösungsfälle.
- Falls ein inhomogenes lineares Gleichungssystem zumindest eine Lösung besitzt, so ist seine allgemeine Lösung
von der Form
wobei
xinh
für eine spezielle (beliebige, aber festgehaltene) Lösung steht und
xhom
die allgemeine Lösung des zugehörigen homogenen Gleichungssystems bezeichnet.
Das bedeutet: Um die allgemeine Lösung (also die vollständige Lösungsmenge) eines inhomogenen Systems anzugeben,
muss nur eine einzige seiner Lösungen und die allgemeine Lösung des zugehörigen homogenen Systems
bekannt sein.
- Ein lineares Gleichungssystem mit m = n = 2
(also 2 Gleichungen in zwei Variablen) besitzt genau dann eine einzige Lösung, wenn
gilt. Ist hingegen
a11a22 – a12a21 = 0,
so gibt es entweder unendlich viele Lösungen oder keine Lösung.
Die Größe
a11a22 – a12a21,
von der dies abhängt, ist die Determinante
der aus den a's gebildeten Matrix.
- Ein analoges Kriterium kann für beliebig große lineare Gleichungssysteme formuliert werden, sofern
m = n gilt. Die aus den
a's gebildete Matrix heißt dann
quadratisch (weil Sie ein quadratisches Zahlenschema bildet), und aus ihr kann ebenfalls eine Größe
gebildet werden, die Determinante heißt. Ist m = n = 3,
so kann die Determinante mit der so genannten Regel von Sarrus (ausgesprochen: "Sarrü")
|
a11a22a33
+ a13a21a32
+ a31a12a23
– a13a22a31
– a11a23a32
– a12a21a33
|
|
|
(27) |
berechnet werden. Je größer das Gleichungssystem, umso komplizierter wird die Formel für die Determinante.
(Wir verzichten hier darauf, die allgemeine Regel für ihre Berechnung anzugeben).
In jedem Fall gilt stets: Das Gleichungssystem besitzt genau dann eine einzige Lösung,
wenn die Determinante ≠ 0 ist.
Hinter all diesen sehr abstrakt formulierten Eigenschaften stecken einige einfache geometrische Sachverhalte, denen wir uns
nun zuwenden.
|
| | |

Vektorräume
(in Vorbereitung)

Determinante
| |
| | |
| Lineare Gleichungssysteme geometrisch interpretieren |
| | | |
Zum Seitenanfang | |
| | |
Lineare Gleichungssysteme können auf einfache Weise geometrisch gedeutet werden.
Die Interpretation, die wir nun besprechen, klärt auch auf eine der Vorstellung leicht
zugängliche Weise auf, warum es manchmal nur eine, manchmal unendlich viele und manchmal gar
keine Lösung gibt – und warum es nie eine andere Zahl von Lösungen geben kann.
Weiters ist sie hilfreich, wenn wir uns von den Lösungsmengen,
die unendlich viele Elemente besitzen, ein Bild machen wollen.
| | | |
| |
| | |
Geradengleichungen
Beginnen wir mit einer einzigen linearen Gleichung in zwei Variablen, die wir
x und
y nennen. Eine Lösung ist ein
(reelles) Zahlenpaar (x, y),
das sie erfüllt. Ein Zahlenpaar können wir aber als Punkt in der Zeichenebene
darstellen, dessen Koordinaten x und
y sind. Die Menge aller Zahlenpaare ist die
Zeichenebene selbst. Daher kann die Lösungsmenge einer linearen Gleichung als
Teilmenge der Zeichenebene aufgefasst werden und bekommt damit unmittelbar einen geometrischen
Charakter.
Welche Arten von Teilmengen treten als Lösungsmengen linearer Gleichungen auf?
Wie im ersten Kapitel über analytische Geometrie dargestellt, handelt es sich
um Geraden. Mit anderen Worten: Eine lineare Gleichung in zwei Variablen kann als
Geradengleichung interpretiert werden. Das trifft natürlich auch auf alle
linearen Gleichungen zu, die wir in diesem Kapitel bisher hingeschrieben haben, etwa
(2), was äquivalent zu (2') ist, oder (6)
oder (7a) oder (7b). Eine lineare Gleichung in
zwei Variablen kann stets in die Form
| | | |

Zeichenebene und Koordinatensystem

Geradengleichungen
| |
| | |
gebracht werden (was nichts anderes als (4) für n = 2
ist). Dabei wollen wir voraussetzen, dass von den beiden Konstanten
a und
b zumindest eine
≠ 0 ist.
Wie die Konstanten, die hier auftreten, mit der Lage der Geraden zusammenhängen,
wurde im Geometriekapitel im Zusammenhang mit den Geradengleichungen eingehend besprochen. Hier nur eine Zusammenfassung der
Ergebnisse:
| | | |
| |
| | |
- Ist c = 0, so verläuft die
durch (28) beschriebene Gerade (genauer: die Gerade, die die Lösungsmenge von
(28) geometrisch darstellt) durch den Ursprung.
Ist c ≠ 0, so verläuft sie
nicht durch den Ursprung.
- Ist a = 0 (und daher
b ≠ 0), so können wir
(28) zu
y = c/b umformen.
Die Gerade verläuft dann parallel zur
x-Achse, und zwar bei einem
y-Wert von
c/b.
Ist zusätzlich c = 0, so
handelt es sich um die x-Achse.
- Ist b = 0 (und daher
a ≠ 0), so können wir
(28) zu
x = c/a umformen.
Die Gerade verläuft dann parallel zur
y-Achse, und zwar bei einem
x-Wert von
c/a.
Ist zusätzlich c = 0, so
handelt es sich um die y-Achse.
- Ist
b ≠ 0, so kann
(28) nach y
aufgelöst, also in der Form
y = k x + d
geschrieben werden, wobei
k = – a/b
(der Anstieg oder die Steigung)
d = c/b
(der "Abschnitt auf der y-Achse" oder
Ordinaten-Abschnitt)
ist. Diese beiden Konstanten bestimmen den Verlauf der Geraden nach der folgenden Regel:
Sie schneidet die y-Achse im Punkt
(0, d).
Ihre Richtung bestimmt sich durch die Regel "1 nach rechts
und k hinauf".
Ist k < 0, so bedeutet die letzte Regel:
"|k| hinunter".
- Gilt a ≠ 0,
b ≠ 0 und
c ≠ 0, so kann die Lage der
Geraden durch die Punkte bestimmt werden, in denen sie die Achsen schneidet:
Sie schneidet die x-Achse im Punkt
(c/a, 0).
Sie schneidet die y-Achse im Punkt
(0, c/b).
- Die Koeffizienten a
und b bestimmen die Richtung der Geraden.
Jener Vektor, dessen Komponenten sie sind, also
n = (a, b),
steht stets normal auf die Gerade (und heißt daher Normalvektor).
| | | |

Normalvektor

Normalvektorform
der Geraden
| |
| | |
Ist b ≠ 0, so können Sie
sich schnell über die Lage der Geraden orientieren, indem Sie die Gleichung nach
y auflösen und den
erhaltenen Ausdruck (der immer die Form k x + d
hat) in einen Funktionsplotter, beispielsweise in den
eingeben. Um etwa die durch die Gleichung
y = 2x – 1
definierte Gerade anzuzeigen, tippen Sie
2*x-1
ein! Mit diesem Tool können Sie auch mehrere Geraden gleichzeitig anzeigen
(was im Folgenden von Bedeutung sein wird).
| | | |
| |
| | |
Lineare Schnittprobleme in der Ebene
Wenn die Lösungsmenge einer linearen Gleichung in zwei Variablen geometrisch als Gerade dargestellt werden kann,
so ist die Lösungsmenge eines linearen Gleichungssystems in zwei Variablen – die ja die Durchschnittsmenge der
Lösungsmengen der einzelnen Gleichungen ist – nicht anderes als die Schnittmenge der Geraden,
die die einzelnen Gleichungen darstellen. Wir beschränken uns auf den Fall, dass das System aus zwei
linearen Gleichungen besteht. Die Lösungsmenge ist dann einfach die Schnittmenge zweier Geraden! Das ist der
geometrische Hintergrund, der bei den linearen Gleichungssystemem mitschwingt und praktisch alle ihre
Eigenschaften erklären kann! Im Fall von mehr als zwei Variablen oder mehr als
zwei Gleichungen muss er nur ein bisschen verallgemeinert werden, aber die zentrale Idee haben wir bereits hier
offen vor uns liegen!
Gemoetrisch läuft das Lösen eines Systems von zwei linearen Gleichungen in zwei Variablen also
darauf hinaus, die Schnittmenge zweier Geraden zu ermitteln. Wie das recherisch zu bewerkstelligen ist,
haben wir in diesem Kapitel bereits besprochen (denn ein solches lineares Schnittproblem in der Ebene zu lösen
besteht gerade darin, ein Gleichungssystem zu lösen). Wir wenden uns nun der Frage zu,
was es geometrisch bedeutet. Wie kann die Schnittmenge zweier Geraden in der Zeichenebene aussehen?
Drei Fälle sind möglich:
- Die beiden Geraden sind nicht zueinander parallel. Sie haben dann einen einzigen Punkt gemeinsam, ihren
Schnittpunkt.
- Die beiden Geraden sind zueinander parallel und voneinander verschieden. Sie haben keinen Punkt gemeinsam.
- Die beiden Geraden sind identisch. Da sie in Wahrheit nur eine einzige Gerade sind, haben sie unendlich viele Punkte gemeinsam.
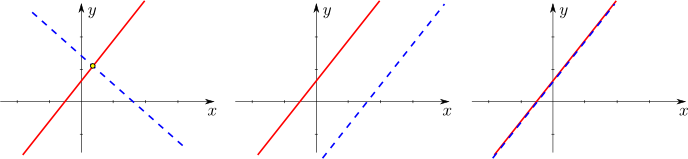
Erkennen Sie, dass diese möglichen Lagebeziehungen von zwei Geraden in der Ebene
genau den drei grundsätzlich möglichen Lösungsfällen entsprechen, die uns bei den
linearen Gleichungssystemen immer begegnet sind? Um sich die geometrische Bedeutung eines konkreten Gleichungssystems
in zwei Variablen vor Augen zu halten, müssem Sie zuerst die Geraden bestimmen, die den einzelnen Gleichungen
entsprechen (d.h. deren Lösungsmengen sie darstellen). Die Schnittmenge dieser Geraden (also die Menge aller
Punkte, die sie gemeinsam besitzen) gibt dann die
Lösungsmenge des gesamten Gleichungssystems an, und klarerweise sollte sie mit dem Ergebnis Ihrer Berechnung
übereinstimmen.
Im ersten Geometriekapitel wurden die Lagebeziehungen und Schnittmengen von Geraden in der Ebene
ausführlich diskutiert – sehen Sie sich den entsprechenden Abschnitt als Ergänzung an!
| | | |

Lagebeziehungen von Geraden in der Ebene
| |
| | |
Auf diese Weise spielen lineare Gleichungssysteme in zwei Variablen und lineare Schnittproblem in der Ebene
zusammen. Sie sind praktisch identisch! Wollen Sie ein solches Gleichungssystem lösen, so können Sie
die betreffenden Geraden zeichnen (oder plotten) und die Schnittmenge (insbesondere, wenn es
sich um einen einzigen Punkt handelt) zumindest näherungsweise ablesen. Wollen Sie umgekehrt die Schnittmenge zweier Geraden
in der Zeichenebene durch eine Rechnung ermitteln, so müssen Sie ein lineares Gleichungssystem lösen.
Wir kommen noch kurz auf den (rechnerisch etwas unangenehmen) Fall zurück, dass ein lineares Gleichungssystem in zwei
Variablen unendlich viele Lösungen besitzt.
Gehen Sie die oben durchgeführte rechnerische Lösung des Gleichungssystem (13a) – (13b)
noch einmal unter diesem Gesichtspunkt durch:
- Das ganze System hat sich als zur einzigen Gleichung (13a)
äquivalent erwiesen. Auf diese Weise haben wir rechnerisch gezeigt, dass(13a) und (13b),
als Geradengleichungen aufgefasst, die gleiche Gerade beschreiben!
- Wir haben die Lösungsmenge dieses Systems auch in der Form (14) angeschrieben.
Welche Bewandtnis hat es damit? Auch das ist leicht aufgeklärt:
Im ersten Geometriekapitel wurde die Parameterdarstellung von Geraden in der Ebene eingeführt.
Wir wollen dieses Thema hier nicht wiederholen, sondern bemerken lediglich, dass die Form der
allgemeinen Lösung (14) nichts anderes ist als eine Parameterdarstellung der Lösungsgeraden
(mit x als Parameter).
Nun liegt es schon fast in der Luft, wie Gleichungssysteme in drei Variablen
geometrisch zu deuten sind.
| | | |

Parameterdarstellung von Geraden in der Ebene
| |
| | |
Ebenengleichungen
Im zweiten Geometriekapitel wurde die analytische (d.h. rechnerische) Darstellung von Ebenen im Raum
behandelt. Es ist an dieser Stelle wahrscheinlich nicht überraschend, dass Ebenen im Raum genau die
Lösungsmengen von linearen Gleichungen in drei Variablen sind. Jede lineare Gleichung in drei Variablen
| | | |

Beschreibung von Ebenen
| |
| | |
(wobei wir die Koeffizienzen nun mit
p, q
und r bezeichnet haben)
kann geometrisch als Ebenengleichung gedeutet werden. Wir wollen hier nicht in die Details
der Lagebestimmung einer Ebene aus ihrer Gleichung eindringen, sondern erwähnen nur drei Aspekte:
- Ist c = 0, so liegt der Ursprung auf der Ebene.
Ist c ≠ 0, so liegt der Ursprung nicht
auf der Ebene.
- Die Koeffizienten p,
q
und r bestimmen die Ausrichtung der Ebene im Raum.
Jener (dreidimensionale) Vektor, dessen Komponenten sie sind, also
n = (p, q, r),
steht stets normal auf die Ebene (und heißt daher Normalvektor).
- Die Gleichung z = 0 beschreibt die
xy-Ebene, und Analoges gilt für die zwei
anderen Koordinatenebenen.
Ebenen im Raum können wir uns zwar einigermaßen gut vorstellen, aber wir können sie nicht
so gut zeichnen wie Geraden. Eines ist aber auf jeden Fall klar: Zwei Ebenen, die nicht zueinander parallel sind,
schneiden einander in einer Geraden, und daher müssen wir uns kurz mit der Darstellung von
Geraden im Raum befassen.
| | | |

Ebenengleichung

Normalverktorform
der Ebene
| |
| | |
Geraden im Raum
Eine Gerade im Raum kann nicht durch eine lineare Gleichung in den drei Raumkoordinaten beschrieben werden
(denn jede solche Gleichung stellt, wie soeben diskutiert, eine Ebene dar).
Statt dessen gibt es eine andere Methode: die Parameterdarstellung von Geraden im Raum.
Wir wollen auch dieses Thema hier nicht wiederholen, sondern verweisen
auf das erste Geometriekapitel, in dem es eingeführt und diskutiert wurde.
| | | |

Parameterdarstellung von Geraden im Raum
| |
| | |
Lineare Schnittprobleme im Raum
Wenn die Lösungsmenge einer linearen Gleichung in drei Variablen geometrisch als Ebene im Raum dargestellt werden kann,
so ist die Lösungsmenge eines linearen Gleichungssystems in drei Variablen – die ja die Durchschnittsmenge der
Lösungsmengen der einzelnen Gleichungen ist – nicht anderes als die Schnittmenge der Ebenen,
die die einzelnen Gleichungen darstellen. Gemoetrisch läuft das Lösen eines linearen Gleichungssystems in drei Variablen also
darauf hinaus, die Schnittmenge aller Ebenen zu ermitteln, die den einzelnen Gleichungen entsprechen.
Wir das recherisch zu bewerkstelligen ist,
haben wir in diesem Kapitel bereits besprochen (denn ein solches lineares Schnittproblem im Raum zu lösen
besteht gerade darin, ein Gleichungssystem zu lösen).
Wir wenden uns nun der Frage zu, was es geometrisch bedeutet. Wie sehen die möglichen
Lagebeziehungen und Schnittmengen von Ebenen im Raum aus?
Diese Fragen werden im zweiten Geometriekapitel ausführlich diskutiert. Daher
beschränken wir uns hier auf die wesentlichen Aspekte.
| | | |

Lagebeziehungen
von Ebenen
| |
| | |
Zuerst betrachten wir den
Fall von nur zwei Ebenen:
- Zwei Ebenen schneiden einander entweder überhaupt nicht oder in einer Geraden – je nachdem,
ob sie zueinander parallel sind oder nicht:
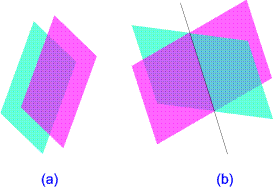
Die Lösungsmenge eines Systems von nur zwei linearen Gleichungen in drei Variablen ist daher entweder
leer oder eine Gerade.
Haben wir nun ein System von drei linearen Gleichungen in drei Variablen (also das Problem der Schnittmenge
dreier Ebenen) vor uns, so gibt es eine Reihe von Lagebeziehungen (die den Lösungsfällen entsprechen):
- Der einfachste Fall besteht darin, dass die drei Ebenen einen einzigen Punkt gemeinsam haben.
Wir können die Situation so andenken: Die ersten beiden Ebenen schneiden einander in einer
Geraden, und diese durchstößt die dritte Ebene in einem Punkt.
Das ist beispielsweise das Fall für das oben diskutierte Gleichungssystem
(20a) – (20c).
- Die drei Ebenen besitzen keinen Punkt gemeinsam. Es gibt zwei mögliche Gründe für
eine solche Situation:
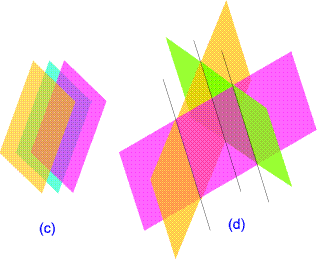
Rechnerisch bemerken wir das, indem wir beim systematischen Lösen des entsprechenden Gleichungssystems
auf einen Widerspruch stoßen.
- Weiters können die drei Ebenen einander in einer Geraden schneiden.
Das tritt dann ein, wenn die Schnittgerade zweier dieser Ebenen in der dritten Ebene liegt:

Rechnerisch bemerken wir das, wenn sich beim systematischen Lösen des entsprechenden Gleichungssystems
herausstellt, dass es zu einem System mit nur zwei linearen Gleichungen äquivalent ist.
Die beiden Gleichungen dieses reduzierten Systems stellen Ebenen dar, deren Schnittmenge die gesuchte Lösungsmenge ist.
Das oben diskutierte Gleichungssystem
(21a) – (21c)
ist von diesem Typ. Es ist äquivalent zu dem System, das nur aus
(21d) und (21g) besteht.
Die Form (22) der allgemeinen Lösung ist nichts anderes als eine
Parameterdarstellung der Lösungsgeraden (mit z
als Parameter).
Und auch in (18a) – (18b) wurde angenommen, dass
ein vereinfachtes Gleichungssystem nur aus zwei Gleichungen besteht.
Die Form (19) der allgemeinen Lösung ist eine
Parameterdarstellung der Lösungsgeraden (mit x
als Parameter).
- Schließlich kann der Fall eintreten, dass alle drei Ebenen identisch sind. (Dafür brauchen wir kein Bild!)
Rechnerisch merken wir das, indem sich beim systematischen Lösen des entsprechenden Gleichungssystems
herausstellt, dass es zu einer einzigen linearen Gleichung äquivalent ist.
Das bedeutet, dass alle drei Ebenengleichungen ineinander umgeformt werden können
Ein derartiges System haben wir nicht durchgerechnet, aber in (16) wurde angenommen, dass
ein vereinfachtes Gleichungssystem lediglich aus der einzigen Gleichung besteht.
Die Form (17) der allgemeinen Lösung ist nichts anderes als eine
Parameterdarstellung der Lösungsebene (mit x
und y als Parameter), ein Konzept,
das im zweiten Geometriekapitel besprochen wird.
| | | |

Parameterdarstellung der Ebene
| |
| | |
Damit haben wir eine der schönsten mathematischen Querverbindungen offengelegt: die zwischen linearen
Gleichungssystemen und linearen Schnittproblemen. Was geometrisch bei linearen Gleichungssystemen in mehr als drei Variablen geschieht,
können wir uns weniger gut vorstellen, aber im Grunde sind es ganz ähnliche Dinge wie die bisher
besprochenen.
| | | |
| |
| | |
Noch ein bisschen Theorie
Dieser Unter-Abschnitt kann von
''EinsteigerInnen'' ausgelassen werden.
Auch die obigen theoretischen Betrachtungen erfahren nun
eine geometrische Aufklärung:
| | | |
| |
| | |
- Insbesondere ist nun aus geometrischen Gründen klar, dass es immer nur eine, keine oder unendlich viele Lösungen
geben kann.
- Die Lösungsmenge eines linearen Gleichungssystems in beliebig vielen Variablen
(sofern sie nicht aus einem einzigen Punkt besteht oder leer ist) ist stets ein "lineares"
oder "flaches" Gebilde (eine Gerade, eine Ebene, eine Hyperebene, eine Hyperhyperebene,...).
Ist das Gleichungssystem homogen, so enthält es den Ursprung.
- Es wurde oben erwähnt, dass die
Lösungsmenge eines homogenen linearen Gleichungssystems immer ein Vektorraum ist. Das wurde durch die
Eigenschaft (24) ausgedrückt. Geometrisch betrachtet handelt
es sich dabei entweder um den Ursprung oder um ein "lineares" Gebilde (eine Gerade, eine Ebene, eine Hyperebene,
eine Hyperhyperebene,...), in dem der Ursprung liegt. All dies sind Mengen, mit der Eigenschaft, dass
beliebige Linearkombinationen von Ortsvektoren nicht aus ihnen herausführen. Genau das macht einen
Vektorraum aus.
- Die Form (25) der allgemeinen Lösung eines inhomogenen linearen Gleichungssystems
mit nichtleerer Lösungsmenge erfährt nun auch ihre geometrische Aufklärung: Der Anteil
xinh
stellt eine "Verschiebung" der Lösungsmenge des zugehörigen homogenen Gleichungssystems
dar. Geometrisch betrachtet, ist die Lösungsmenge des inhomogenen Systems eine Gerade, eine Ebene, eine Hyperebene,
eine Hyperhyperebene,..., auf der der Ursprung nicht liegt. Mengen dieser Art sind zwar keine Vektorräume,
aber wir können sie uns als "verschobene Vektorräume" vorstellen. (Sie werden auch
affine Räume genannt).
- Die Sache mit der Determinante (siehe (26) und (27)) ist weniger anschaulich aufzuklären,
aber es ist einen Versuch wert: Die Determinante ist genau dann
≠ 0, wenn die
Normalvektoren auf die Geraden, Ebenen, Hyperebenen,..., die den einzelnen Gleichungen entsprechen,
ein nichtverschwindendes Volumen (im Sinn von Fläche, Volumen, Hypervolumen,...) aufspannen.
Einige weitere Aspekte dieser Strukturen werden in zwei späteren Kapiteln
besprochen..
|
| | |

Ortsvektor

Lineare Algebra
(in Vorbereitung)

Mathematische Strukturen und
Räume
(in Vorbereitung)
| |
| | |
| Nichtlineare Gleichungssysteme |
| | | |
Zum Seitenanfang | |
| | |
Nichtlineare Gleichungssysteme können beliebig kompliziert sein. Wir beschränken uns hier auf
einfache Systeme in zwei und drei Variablen, die höchstens quadratisch in den Variablen sind, und
(mehr oder weniger) einfache
geometrische Deutung zulassen.
| | | |
| |
| | |
Nichtlineare Schnittprobleme in der Ebene
Die Lösungsmengen nichtlinearer Gleichungen in zwei Variablen können – ebenso wie jene linearer
Gleichungen – als Teilmengen der Zeichenebene dargestellt (und vorgestellt) werden. Da diesem Thema das
dritte Geometriekapitel gewidmet ist, fassen wir uns kurz. Die folgende Liste führt
einige nichtlineare Gleichungen in zwei Variablen und die geometrische Darstellung ihrer Lösungsmengen
an:
| Gleichung |
Lösungsmenge |
| x2 + y2 = r2 |
Kreis mit Mittelpunkt im Ursprung und Radius r. |
| (x – p)2 + (y – q)2 = r2 |
Kreis mit Mittelpunkt im Punkt (p, q) und Radius r. |
| x2/a2 + y2/b2 = 1 |
Ellipse in Hauptlage mit Halbachsen a und b.
Verschobene Ellipsen werden analog zum Kreis erhalten. |
x2/a2 – y2/b2 = 1
–x2/a2 + y2/b2 = 1 |
Hyperbeln in Hauptlage mit Halbachsen a und b.
Verschobene Hyperbeln werden analog zum Kreis erhalten. |
x2 = 2py
y2 = 2px |
Parabeln in Hauptlage mit Parameter p.
Verschobene Parabeln werden analog zum Kreis erhalten. |
| ax2 + rx + by2 + sy + txy = c |
Je nach den Werten der Konstanten
a,
b,
r,
s und
t: Gerade, Ellipse (Spezialfall: Kreis), Hyperbel, Parabel (alle in beliebiger
Lage, auch verdreht) oder ein Grenzfall wie ein einzelner Punkt oder zwei einander schneidende Geraden. |
Insbesondere die letzte dieser Gleichungen (die allgemeine – höchstens quadratische – Gleichung in zwei Variablen) zeigt, wie
reichhaltig die hier auftretenden Lösungsmengen sind.
Die Lösungsmengen von Gleichungssystemen, die aus derartigen Gleichungen bestehen, sind also die Schnittmengen der entsprechenden
geometrischen Figuren. Einige Fälle sind von allgemeiner Relevanz, wie beispielsweise das System
dessen Lösung, geometrisch interpretiert, auf die Bestimmung der Schnittmenge eines Kreises mit einer
Geraden hinausläuft. Die gegebene Lösungsmethode ist hier das Substitutionsverfahren: Wird
(30b) in (30a) eingesetzt, so ensteht eine quadratische
Gleichung in x, die (zunächst formal)
gelöst werden kann. Versuchen Sie es selbst!
Dabei sollte die Wurzel aus der Kombination
(1 + k2) r2 – d2
auftreten. Ist diese Größe positiv, so gibt es zwei Lösungen (also zwei Schnittpunkte).
Ist sie negativ, so gibt es keine Lösung (also keinen gemeinsamen Punkt). Ist sie gleich
0, so gibt es genau eine Lösung, also genau einen
gemeinsamen Punkt, in dem die Gerade den Kreis berührt. Das Kriterium
| | | |

Analytische
Geometrie 3
(in Vorbereitung)
| |
| | |
wird daher als Berührbedingung bezeichnet.
Ähnliche Überlegungen können mit Ellipsen, Hyperbeln und Parabeln angestellt werden.
| | | |

Berührbedingungen
(in Vorbereitung)
| |
| | |
Nichtlineare Schnittprobleme im Raum
Abschließend erwähnen wir, dass Gleichungssysteme in drei Variablen, die höchstens quadratisch in den
Variablen sind, als Schnittprobleme bestimmter Flächen im Raum gedeutet werden können, nämlich von
Ebenen, Sphären (Kugeloberflächen), Ellipsoiden, Hyperboloiden und Paraboloiden
(sowie einigen Grenzfällen wie Doppelkegeln und Zylindern) – mit einem Wort: den räumlichen
Verallgemeinerungen von Geraden, Kreisen, Ellipsen, Hyperbeln und Parabeln.
Hier nur einige wenige Beispiele:
| Gleichung |
Lösungsmenge |
| x2 + y2 + z2 = r2 |
Sphäre mit Mittelpunkt im Ursprung und Radius r. |
| (x – p)2 + (y – q)2 + (x – s)2 = r2 |
Sphäre mit Mittelpunkt im Punkt (p, q, s) und Radius r. |
| x2/a2 + y2/b2 + z2/c2 = 1 |
Ellipsoid in Hauptlage mit Halbachsen a, b und c. |
| x2 + y2 – z2 = 1 |
Einschaliges Hyperboloid. |
| x2 + y2 – z2 = –1 |
Zweischaliges Hyperboloid. |
| x2 + y2 – z2 = 0 |
Doppelkegel. |
| z = x2 + y2 |
Paraboloid. |
Hier 3D-Darstellungen des einschaligen und zweischaligen Hyperboloids, des Doppelkegels sowie des Paraboloids entsprechend den oben angegebenen
Gleichungen:

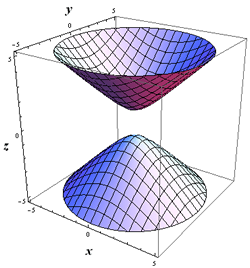


| | | |

Flächen im Raum
(in Vorbereitung)
| |
| | |
Relevante Systeme von Gleichungen dieses Typs betreffen die Schnittmengen des Doppelkegels mit Ebenen, die auf die
Kegelschnitte (Ellipse, Hyperbel und Parabel) führen.
Hier eine 3D-Darstellung, die zeigt, wie die Hyperbel als eine solche Schnittmenge entsteht:

Wird die Bedingung "höchstens quadratisch in den Variablen" fallen gelassen, so handelt man sich
Schnittprobleme mit weitgehend beliebigen Flächen ein, die auch beliebig kompliziert sein können.
|
| | |

Kegelschnitte
(in Vorbereitung)
| |
| | |
| Gleichungssysteme mit dem Computer lösen |
| | | |
Zum Seitenanfang | |
| | |
Zum (exakten oder näherungsweisen) Lösen von Gleichungssystemen steht eine Reihe elektronischer Tools
zur Verfügung, die aber in der Regel unterschiedlich "schlau" sind. Wir müssen bedenken, dass
sich ein Computerprogramm im Allgemeinen leicht tun, wenn es endlich viele Dinge, die durch Zahlen
ausgedrückt werden können, finden soll. Wie gut es die unterschiedlichen Lösungsfälle, die
bei Gleichungssystemen auftreten können (insbesondere wenn unendlich viele Lösungen existieren),
erkennt, hängt sehr davon ab, wie es programmiert ist, und aus welchen Typen von Gleichungen
das System besteht. Am besten können das Computeralgebra-Systeme (CAS).
Für die rechnerische Lösung (ohne grafische Darstellung) können Sie unser Tool
Online-Rechnen mit Mathematica
benutzen:
- Wählen Sie die Kategorie "Gleichungssystem lösen" und danach eine der angebotenen Operationen
"Gleichungssystem exakt lösen" oder "Gleichungssystem numerisch lösen"!
- Geben Sie die Variablen als Liste mit geschwungenen Klammern an, also beispielsweise
{x,y} oder
{x,y,z}!
Sie können dabei beliebige Variablennamen verwenden.
- Geben Sie das zu lösende Gleichungssystem in das Feld "Eingabe" ebenfalls
als Liste mit geschwungenen Klammern an, also beispielsweise
{2x+3y=4,x-9y=16}
oder
{2x+3y-8z=4,x-9y+z=16,3x+4y-3z=1}!
- Klicken Sie auf den Button "Ausführen"!
Mathematica gibt die Lösung(en) als Regeln mit Zuordnungspfeilen aus.
- Falls lediglich das Symbol {} ausgegeben wird, ist die
Lösungsmenge leer.
- Manchmal (insbesondere, wenn es keine eindeutige Lösung gibt) schreibt Mathematica vor der Ausgabe
eine Warnung wie
Solve::svars: Equations may not give solutions for all "solve" variables.
In den meisten Fällen ist die Ausgabe aber korrekt.
- Die Zahl der Gleichungen muss nicht mit der Zahl der Variablen übereinstimmen.
- Sie können auch Gleichungssysteme eingeben, die unbestimmte Konstanten enthalten, wie etwa
{2x+3ay=4,x-9y=16}
mit den Variablen {x,y}. Aber Achtung: Die Lösungsmenge
kann von den genauen Werten dieser Konstanten abhängen, was Mathematica nicht immer berücksichtigt.
So liefert das Programm für das Gleichungssystem {x+y=a,x+y=b}
mit den Variablen {x,y}
die leere Menge, obwohl das für die spezielle Wahl
a = b
nicht stimmt.
- Sie können auch nichtlineare Gleichungssysteme eingeben, sofern nur Polynome vorkommen.
Versuchen Sie etwa {x+y^2=1,y+x=3}!
Die Ausgabe kann bei derartigen Gleichungen aber auch recht lang sein: Versuchen Sie
{x^2+y^2=1,y^3+x^2=3}!
Das Symbol Root in der Ausgabe bezeichnet die Quadratwurzel, und
I steht für die imaginäre Zahl
i, die auftritt, wenn die Wurzel aus einer
negativen Zahl gezogen wird. Falls in der Ausgabe das Symbol Root vorkommt, gibt
es keine geschlossene (also durch die üblichen mathematischen Operationen ausdrückbare) Lösung.
| | | |

komplexe Zahlen
(in Vorbereitung)
| |
| | |
Auf der Webseite
WolframAlpha
(die im Hintergrund ebenfalls mit Mathematica arbeitet) können Sie ein Gleichungssystem einfach in der Form
2x+3y=7,x+4y=-3
oder
2x+3y^2=7,2x^2+3y=7
oder
2x+3y-z=7,x+y-2z/2=3,3x+y-z=1
eingeben. Die Lösung wird manchmal in exakter, manchmal in näherungsweiser
Form angegeben. Im Fall eines Systems von zwei Gleichungen bekommen Sie auch gleich eine
grafische Darstellung mitgeliefert.
Für lineare Systeme von gleich vielen Variablen wie Gleichungen und
den speziellen Fall, dass es eine eindeutige Lösung gibt, stehen auch andere Online-Tools
zur Verfügung, wie die Seite
Rechner zum Lösen linearer Gleichungssysteme
von Arndt Brünner. Achtung bei Eingabe von Bruchzahlen als Koeffizienten: Statt
(2/3)x
oder
2x/3
muss
2/3x geschrieben werden!
Darüber hinaus kann zu jedem eingegebenen Gleichungssystem ein detailliertes Lösungsprotokoll generiert werden,
und es können zum Üben Zufalls-Gleichungssysteme mit Lösungen erzeugt werden.
|
| | |
| |