| | |
| | | |
| |
| | |
| Wiederholung: die reellen Zahlen |
| | | |
| |
| | |
Wenn Sie sich bis zu diesem Kapitel vorgearbeitet haben, wissen Sie wahrscheinlich bereits viel über die reellen Zahlen.
Vielleicht ist Ihnen die Menge der reellen Zahlen als die umfassendste Zahlenmenge erschienen, die es gibt. Fassen wir einige wichtige
Tatsachen zusammen, die diese Zahlenmenge betreffen:
Zahlengerade, Addition und Multiplikation:
- Jede reelle Zahl besitzt eine Dezimaldarstellung, die ihr einen eindeutigen und präzise bestimmten Ort auf der
Zahlengeraden zuweist. Die Zahlengerade repräsentiert daher die Menge $\mathbb{R}$ aller reellen Zahlen.
Sie ist nicht zuletzt deshalb ein nützliches Konzept, weil sie uns erlaubt, uns die reellen Zahlen geometrisch vorzustellen.
- Reelle Zahlen können addiert werden ($2+3=5$).
- Reelle Zahlen können multipliziert werden ($2\cdot 3=6$).
- Die Addition und die Multiplikation reeller Zahlen gehorchen Rechenregeln, die wir normalerweise – auch im Alltag – anwenden,
ohne sie großartig zu hinterfragen. Addition und Multiplikation sind kommutativ, d.h. sie hängen nicht von der Reihenfolge
ab (wie die Beispiele $2+3=3+2$ und $2\cdot 3=3\cdot 2$ illustrieren), und sie sind assoziativ, d.h.die Addition und die Multiplikation
dreier reeller Zahlen hängt nicht davon ab, wie wir sie gruppieren:
|
\begin{eqnarray}
\underbrace{(2+3)}_{5}+4&=&2+\underbrace{(3+4)}_{7}\\
\underbrace{2\cdot 3}_{6}\cdot 4&=&2\cdot\underbrace{3\cdot 4}_{12}
\end{eqnarray}
|
|
|
$(1)$ |
Daher können wir $2+3+4$ und $2\cdot 3\cdot 4$ schreiben, ohne eine Gruppierung angeben zu müssen.
Weiters spielen die beiden Operationen auf eine sehr praktische Weise zusammen:
Das so genannte Distributivgesetz, durch das Beispiel
|
$$2\cdot\underbrace{(3+4)}_7=\underbrace{2\cdot 3}_{6}+\underbrace{2\cdot 4}_{8}$$
|
|
|
$(2)$ |
illustriert, ist die Grundlage für das Rechnen mit Klammern.
- Es gibt zwei besondere reelle Zahlen: die Null und die Eins, deren Rollen in Bezug auf die beiden Operationen durch
$5+0=5$ und $5\cdot 1=5$ verdeutlich werden.
| | | |

reelle Zahlen

Zahlengerade
| |
| | |
Subtraktion und Division:
- Im Rahmen der reellen Zahlen können Gleichungen formuliert werden. Sie erlauben uns, zu
subtrahieren. Beispielsweise ist die durch die Subtraktion $7-2$ bezeichnete reelle Zahl die (einzige) Lösung
der Gleichung
Auch Kinder lösen Gleichungen, indem sie das Subtrahieren in Form von Fragen wie "2 und wieviel ist 7" lernen.
- Das Dividieren funktioniert auf ähnlich Weise. So ist etwa die durch die Division $7:2$ (oder $7/2$ oder $7\over 2$)
bezeichnete reelle Zahl die (einzige) Lösung der Gleichung
Beim Dividieren müssen wir allerdings die Einschränung machen, dass nicht durch $0$ dividiert werden kann. Da etwa
die Gleichung
keine Lösung besitzt, entspricht $7\over 0$ keiner reellen Zahl! Wir können auch sagen, dass $7\over 0$ nicht definiert ist.
Auch $0\over 0$ ist nicht definiert, da die Gleichung $0\cdot x=0$ keine eindeutige Lösung besitzt.
Das Rechnen mit reellen Zahlen bewährt sich auch in Anwendungen (etwa, wenn wir die Fläche eines Rechtecks ermitteln,
indem wir die Seitenlängen abmessen und – in einer beliebigen Reihenfolge – miteinander multiplizieren).
Additionen, Subtraktionen, Multiplikationen und Divisionen (außer durch $0$) von reellen Zahlen ergeben immer wieder reelle Zahlen,
führen aus der Menge der reellen Zahlen also nicht hinaus. Wohin sollten sie auch führen?
Kurzum: Die reellen Zahlen scheinen keinen Wunsch offen zu lassen.
Aber wie so oft, trügt der Schein!
|
| | |

Gleichungen
| |
| | |
| Was sind die komplexen Zahlen? |
| | | |
Zum Seitenanfang | |
| | |
Ein Wunsch, der offen bleibt, ist jener nach einer Zahl, deren Quadrat negativ ist!
Wieso das, könnten Sie jetzt einwenden! Das Quadrat einer rellen Zahl ist stets $\geq 0$, kann also niemals negativ sein.
Etwas abstrakter formuliert bedeutet das, dass nicht jede quadratische Gleichung eine reelle Lösung besitzt.
Das Paradebeispiel dafür ist die Gleichung
Keine reelle Zahl erfüllt sie. Das ist einfach so! Warum sollte man damit unzufrieden sein?
Formulieren wir die Frage so: Was könnten wir mit einer "Zahl" anfangen, deren Quadrat gleich $-1$ ist?
Die Antwort ist: sehr viel! So viel, dass sie als eines der wichtigsten Konzepte der
modernen Mathematik bezeichnet werden kann! Wir werden in diesem Kapitel besprechen, wie man zu einer solchen
"Zahl" kommt, und wir werden Schritt für Schritt einge der Möglichkeiten kennen lernen, die sie bietet.
Eine "Zahl", deren Quadrat gleich $-1$ ist, kann natürlich keine reelle Zahl sein. Es kann sich nur um eine
abstrakte Konstruktion handeln. Beginnen wir damit, anzunehmen, dass es ein solches Ding gibt, und bezeichnen
wir es mit dem Buchstaben $i$. Wir setzen also voraus,
dass
gilt. $i$ wird imaginäre Einheit genannt.
Zudem wollen wir annehmen, dass wir mit diesem Objekt so rechnen können wie mit einer
reellen Zahl. Beim Addieren und Multiplizieren und beim Rechnen mit Klammern können wir es so behandeln,
als wäre es eine reelle Zahl. Wann immer ihr Quadrat auftritt, setzen wir es gleich $-1$.
Wir können also etwa $i$ mit einer reellen Zahl multiplizieren und zum Ergebnis eine
reelle Zahl addieren, also beispielsweise $3+5i$ bilden. Addieren wir $3+5i$ und $6+2i$, so erhalten wir wieder ein solches
Objekt:
|
$$(3+5i)+(6+2i)=3+5i+6+2i=9+7i$$
|
. |
|
$(8)$ |
Interessanterweise gilt das auch für die Multiplikation:
Multiplizieren wir $3+5i$ und $6+2i$ und lösen die Klammer auf, so erhalten wir mit
|
\begin{eqnarray}(3+5i)(6+2i)&=&\underbrace{3\cdot 6}_{18}+\underbrace{3\cdot 2i+5\cdot6 i}_{36i}+10i^2=\\
&=&18+36i+10\underbrace{\,\,i^2\,\,}_{-1}=\\
&=&18+36i-10=8+36i
\end{eqnarray}
|
|
|
$(9)$ |
wieder ein Kombination "reelle Zahl + $i$ reelle Zahl". Objekte dieser Form heißen komplexe Zahlen.
Ganz allgemein ist eine komplexe Zahl von der Form
wobei $x$ und $y$ reelle Zahlen sind. Werden komplexe Zahlen addiert und multipliziert, so sind die
Ergebnisse stets wieder komplexe Zahlen.
| | | |
| |
| | |
Definition der komplexen Zahlen
Die Form (10) legt nahe, wie wir die komplexen Zahlen in einer mathematisch sauberen
Weise definieren können: Eine komplexe Zahl ist nichts anderes als ein reelles Zahlenpaar!
Anstelle von $x+iy$ können wir genauso gut $(x,y)$ schreiben. Nun kann
die Menge aller reellen Zahlenpaare (die Menge $\mathbb{R}^2$) geometrisch als Zeichenebene
dargestellt werden. Indem wir komplexe Zahlen in der soeben beschriebenen Weise addieren und multiplizieren,
haben wir diese Rechenoperationen auf den $\mathbb{R}^2$ übertragen. Die Zeichenebene zusammen mit
diesen Operationen ist die Menge der komplexen Zahlen und wird mit $\mathbb{C}$ bezeichnet.
Wir wollen nun ganz sorgfältig vorgehen, um die komplexen Zahlen, die Gottfried Wilhelm Leibniz
als "Amphibium zwischen Sein und Nichtsein" bezeichnet hat, auf ganz saubere (und zudem einfache) Weise
in den Griff zu bekommen. Fassen wir alles bisher in diesem Kapitel Gesagte als unverbindliche Idee
auf und versuchen wir, ihr eine exakte mathematische Bedeutung zu geben. Wir beginnen also mit
dem $\mathbb{R}^2$ und seinen Elementen, den rellen Zahlenpaaren.
| | | |

Zeichenebene
| |
| | |
Dass zwei reelle Zahlenpaare zueinander addiert werden können, sollte für Sie nichts Neues sein.
Ein Zahlenpaar kann ja als zweidimensionaler Vektor aufgefasst werden, und Vektoren addieren wir einfach komponentenweise.
Die allgemeine Regel dafür lautet:
|
$$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$$
|
. |
|
$(11)$ |
Wenn wir nun vereinbaren, ein reelles Zahlenpaar $(x,y)$ auch in der symbolischen Form $x+iy$ anzuschreiben, so
besagt diese Regel nichts anderes als
|
$$(x_1+i\,y_1)+(x_2+i\,y_2)=x_1+x_2+i\,(y_1+y_2)$$
|
. |
|
$(12)$ |
Sie drückt das aus, was wir zuvor mit der intuitiven Rechnung (8) im Sinn hatten.
Wie ist das aber jetzt mit der Multiplikation? Lässt sich der intuitiven Rechnung (9)
eine Regel für die Multiplikation von Zahlenpaaren zugrunde legen? Ja, und es ist gar nicht schwierig!
Führen wir eine letzte intuitive Berechnung durch, indem wir zwei komplexe Zahlen miteinander multiplizieren
und die Klammer in gewohnter Weise auflösen:
|
\begin{eqnarray}
(x_1+i\,y_1)(x_2+i\,y_2) &=& x_1x_2+i\,x_1 y_2+i\,y_1 x_2+\underbrace{i^2y_1 y_2}_{-y_1 y_2} =\\
&=& x_1x_2-y_1y_2+i\,(x_1 y_2+y_1 x_2)
\end{eqnarray}
|
|
|
$(13)$ |
Das Ergebnis können wir als reelles Zahlenpaar $(x_1x_2-y_1y_2,x_1 y_2+y_1 x_2)$ auffassen. Damit ist die
gesuchte Regel für die Multiplikation von Zahlenpaaren (die komplexe Multiplikation) gefunden:
|
$$(x_1,y_1)(x_2,y_2)=(x_1x_2-y_1y_2,x_1 y_2+y_1 x_2)$$
|
. |
|
$(14)$ |
Mit (11) und (14) sind eine Addition und Multiplikation für reelle Zahlenpaare
festgelegt. Mit diesen beiden Operationen wird die Menge $\mathbb{R}^2$ zur Menge $\mathbb{C}$ der komplexen Zahlen.
Ab sofort werden wir uns auf diese Definitionen beziehen, bewegen uns also auf mathematisch sicherem Boden.
Die "Schreibweise mit $i$" drückt die Identifizierung
|
$$(x,y)\qquad\longleftrightarrow\qquad x+iy$$
|
|
|
$(15)$ |
aus und ist lediglich eine bequeme Konvention, die uns hilft, Rechnungen übersichtlich zu gestalten.
| | | |

Vektoren
+
Addition
von Vektoren
| |
| | |
Sind die komplexen Zahlen Zahlen?
Dass die komplexen Zahlen als "Zahlen" bezeichnet werden, ist eine sprachliche Konvention.
Theoretisch könnte man diese Sprechweise auch ablehnen und sich für Objekte der Form (15),
die gemäß (11) und (14) addiert und multipliziert werden können,
einen anderen Namen ausdenken. Aber es ist aus zwei Gründen sinnvoll, die komplexen Zahlen
als Zahlen zu bezeichnen:
- Der erste Grund besteht darin, dass die komplexen Zahlen viele Eigenschaften mit den reellen Zahlen gemeinsam haben.
Addition und Multiplikation sind kommutativ und assoziativ, und das Distributivgesetz, das das Rechnen mit
Klammern regelt, gilt auch hier. (Wir werden gleich darauf zurückkommen).
- Der zweite Grund besteht darin, dass die Menge der komplexen Zahlen als Erweiterung des reellen Zahlenbereichs aufgefasst
werden kann: Eine komplexe Zahl der Form (15), für die $y=0$ ist, also ein
Zahlenpaar der Form $(x,0)$ kann als reelle Zahl aufgefasst werden.
Unsere Definitionen (11) und (14) reduzieren sich für das Rechnen mit diesen Objekten
auf die gewöhnliche Addition und Multiplikation reeller Zahlen:
|
\begin{eqnarray}
(x_1,0)+(x_2,0)&=&(x_1+x_2,0)\\
(x_1,0)(x_2,0)&=&(x_1 x_2,0)
\end{eqnarray}
|
|
|
$(16)$ |
In diesem Sinn kann die Menge $\mathbb{R}$ der reellen Zahlen als Teilmenge von $\mathbb{C}$ aufgefasst werden.
Geometrisch entspricht sie der $x$-Achse der Zeichenebene. Wir können reelle Zahlen daher als Spezialfälle
komplexer Zahlen ansehen. Die Zahl $1$ wird mit $(1,0)$ identifiziert. Die Zahl $0$ wird mit $(0,0)$
identifiziert, entspricht also dem Urprung der Zeichenebene.
Die komplexe Zahl $i$, die imaginäre Einheit, identifizieren wir mit dem Zahlenpaar
|
$$(0,1)\qquad\longleftrightarrow\qquad i$$
|
|
|
$(17)$ |
In der geometrischen Sichtweise liegt sie auf der $y$-Achse der Zeichenebene.
Ihr Quadrat wird durch die Regel (14) zu
|
$$i^2 \qquad\longleftrightarrow\qquad (0,1)(0,1)=(-1,0) \qquad\longleftrightarrow\qquad -1$$
|
|
|
$(18)$ |
festgelegt, womit wir unseren Ausgangspunkt (7), eine "Zahl", deren Quadrat gleich $-1$ ist,
auf sicheren Boden gestellt haben. Da unsere ersten intuitiven Berechnungen
(8) und (9) auf der Voraussetzung aufgebaut waren, dass hinsichtlich
der Addition und der Multiplikation die gleichen Rechenregeln wie für die reellen Zahlen gelten,
überrascht es nicht, dass die exakten Definitionen (11) und (14)
genau diese Regeln zur Folge haben. Mit ihrer Hilfe ist es nicht schwierig, zu zeigen, dass
die komplexen Rechenoperationen kommutativ und assoziativ sind, und dass das Distributivgesetz gilt
(siehe den nebestehenden Button).
| | | |
| |
| | |
Ebenso wie die Menge $\mathbb{R}^2$ als $\mathbb{C}$ bezeichnet wird, wenn die komplexen Rechenoperationen
(11) und (14) eine Rolle spielen, bekommt auch die Zeichenebene
in diesem Zusammenhang einen anderen Namen: Sie heißt komplexe Zahlenebene,
Gaußsche Zahlenebene oder einfach komplexe Ebene.
Nachdem wir also festgelegt haben, was die komplexen Zahlen sind, können wir ihre Eigenschaften
untersuchen, und wir werden schrittweise Antworten auf die eingangs gestellte Frage finden, was man mit
derartigen Objekten anstellen kann. Im Folgenden werden wir für komplexe Zahlen meist die Schreibweise
$x+iy$ vorziehen. Halten Sie sich aber bitte stets vor Augen, dass es sich dabei
einfach um Zahlenpaare $(x,y)$ handelt, für die mit (11) und (14)
zwei Rechenoperationen definiert sind!
|
| | |
| |
| | |
| Grundrechnungsarten für komplexe Zahlen |
| | | |
Zum Seitenanfang | |
| | |
Bisher haben wir von der Addition und der Multiplikation komplexer Zahlen gesprochen – aber wie sieht
es mit der Subtraktion und der Division aus?
| | | |
| |
| | |
Subtraktion
Das Subhrahieren mit komplexen Zahlen bietet keinerlei Überraschungen, da ja auch die
Addition von komplexen Zahlen, formal durch (11) bzw. (12) festgelegt, im Grunde eine bekannte Operation
(für zweidimensionale Vektoren) ist. Hier ein Beispiel:
|
$$(9+5i)-(3-2i)=9+5i-3+2i=6+7i$$
|
. |
|
$(19)$ |
Insbesondere können wir von jeder komplexen Zahl die "zu ihr negative" komplexe Zahl bilden, wie etwa
$-(2+3i)=-2-3i$.
| | | |
| |
| | |
Division
Spannend wir es erst bei der Division. Können wir eine komplexe Zahl durch eine komplexe Zahl dividieren?
Können wir etwa
|
$\Large 1-4i\over\Large 3+2i$ oder $\Large 1\over\Large i$
|
|
|
$(20)$ |
bilden? Ja, das ist möglich (außer der Division durch $0$)! Im Einzelnen bewerkstelligen wir das mit einem
genialen Trick, den wir anhand eines Beispiels vorführen:
|
\begin{eqnarray}
{1-4i\over 3+2i}&=&{1-4i\over 3+2i}\cdot \underbrace{{3-2i\over 3-2i}}_{1}=
{(1-4i)(3-2i)\over(3+2i)(3-2i)}=\\
&=&{-5-14i\over 13}=-{5\over 13}-{14\over 13}\,i
\end{eqnarray}
|
|
|
$(21)$ |
Sehen Sie sich die Rechnung genau an und führen Sie sie selbst Schritt für Schritt durch! Nachdem der Bruch mit $3-2i$ erweitert wurde,
wird der Nenner zu $(3+2i)(3-2i)$, und dieses Produkt ist gleich $13$, also eine reelle Zahl! Wohin ist das $i$ verschwunden?
Nun, multiplizieren wir die Klammern ganz ausführlich aus:
|
\begin{eqnarray}
(3+2i)(3-2i)&=&3\cdot 3\,\,\underbrace{\,-3\cdot 2i+2\cdot 3i}_{0}-2\cdot 2\underbrace{\,\,i^2\,\,}_{-1}=\\
&=&3^2+2^2=13
\end{eqnarray}
|
|
|
$(22)$ |
Dieser Trick funktioniert immer! Wir erweitern einen zu berechnenden Bruch mit einer komplexen Zahl,
die wir aus dem Nenner gewinnen, indem wir in ihm einfach $i$ durch $-i$ ersetzen.
Es ist nun eine kleine Übung in Termrechnen, zu beweisen, dass das in (21)
erhaltene Ergebnis, wenn wir es als $z$ bezeichnen, die Gleichung
erfüllt. (Führen Sie die Rechnung selbst durch!)
Wir können also mit komplexen Zahlen nach Herzenslust dividieren (außer durch $0$) und erhalten
als Ergebnisse stets wieder komplexe Zahlen! Die allgemeine Regel dafür lautet:
|
$${x_1+iy_1\over x_2+iy_2}={x_1x_2+y_1y_2\over x_2{}^2+y_2{}^2} + i\,\,{x_2y_1-x_1y_2\over x_2{}^2+y_2{}^2}$$
|
. |
|
$(24)$ |
Schreiben Sie sie zur Übung als Rechenregel für Zahlenpaare an!
(Und danach klicken Sie auf den den nebenstehenden Button!)
Diese Formel zeigt übrigens auch an, dass die Division nur dann nicht funktioniert, wenn die Nenner auf der rechten Seite
verschwinden. Das ist nur dann der Fall, wenn $x_2=y_2=0$ ist, was wir auch in der Form $x_2+iy_2=0$ ausdrücken können:
Durch jede komplexe Zahl kann dividiert werden, außer durch $0$.
| | | |
| |
| | |
Realteil, Imaginärteil, komplex konjugieren und Betrag
Der Trick bei der Division (21) hat darauf beruht, dass das Produkt (22) reell ist.
Das war kein Zufall, sondern deutet darauf hin, dass die Ersetzung von $i$ durch $-i$ in einer komplexen Zahl
eine besondere Bedeutung hat. In der Sichtweise der komplexen Zahlen als reeller Zahlenpaare bedeutet das einfach, das Vorzeichen der
$y$-Koordinate umzudrehen. Um über diese Dinge einfacher sprechen zu können, legen wir einige Sprachregelungen
fest. Ist $z=x+iy$ eine komplexe Zahl (als reelles Zahlenpaar: $z=(x,y)$), so bezeichnen wir
als Realteil von $z$ und
als Imaginärteil von $z$. Real- und Imaginärteil einer komplexen Zahl sind reelle Zahlen: Sie sind nichts
anderes als die beiden reellen Zahlen, aus denen das entsprechende Zahlenpaar besteht. In der geometrischen Interpretation der
komplexen Ebene sind sie einfach die Koordinaten des Punktes $(x,y)$.
Dementsprechend werden die Koordinatenachsen als reelle Achse ($x$-Ache) und imaginäre Achse ($y$-Achse)
bezeichnet. Die Punkte auf der reellen Achse entsprechen den reellen Zahlen. Die Punkte auf der imaginären Achse entsprechen
den reellen Vielfachen von $i$. Sie werden imaginäre Zahlen genannt.
Für jede komplexe Zahl $z=x+iy$ (mit $x$ als Realteil und $y$ als Imaginärteil) bezeichnen wir die
komplexe Zahl
als die zu $z$ komplex konjugierte Zahl (oder kurz als komplex Konjugierte von $z$).
Geometrisch entspricht der Übergang von einer komplexen Zahl $z$ zu ihrer komplex Konujgierten $z^*$ einer
Spiegelung an der reellen Achse. Ein wichtiger Spezialfall ist $i^*=-i$.
Zwei komplexe Zahlen heißen zueinander komplex konjugiert, wenn die eine die komplex Konjugierte der anderen
ist. Klarerweise gilt stets $z^{**}=z$. Reelle Zahlen sind dadurch charakterisiert, dass sie mit ihrer komplex Konjugierten übereinstimmen:
$z$ ist genau dann reell, wenn $z^*=z$ gilt. Weiters ist eine komplexe Zahl $z$ genau dann imaginär, wenn $z^*=-z$ gilt.
Was hinter der Rechnung (22) steckt, ist die Tatsache, dass das Produkt einer komplexen Zahl mit
ihrer komplex Konjugierten stets reell ist. Ganz allgemein gilt
|
$$zz^*=(x+iy)(x-iy)=x^2+y^2$$
|
. |
|
$(28)$ |
Rechnen Sie nach! Damit ist der hinter der komplexen Division stehende Trick aufgeklärt. Mit
(28) ist uns aber noch eine weitere, sehr nützliche Sache in die Hände gefallen:
Die rechte Seite ist nichts anderes als das Quadrat des Betrages (d.h. der Länge) des Vektors $(x,y)$.
Wir bezeichnen mit
|
$$|z| =\sqrt{zz^*}\equiv\sqrt{x^2+y^2}$$
|
. |
|
$(29)$ |
| | | |

Betrag eines Vektors
| |
| | |
den (Absolut-)Betrag der komplexen Zahl $z$. Geometrisch kann er als Länge des
Vektors $(x,y)$ gedeutet werden und damit als Abstand des Punktes $(x,y)$ vom Ursprung $(0,0)$.
Für reelle Zahlen stimmt er mit dem, was wir normalerweise unter dem "Betrag einer Zahl" verstehen, überein.
Wichtige Spezialfälle sind $|1|=1$ und $|i|=1$.
Unter Ausnutzung dieser Bezeichnungen finden wir mit
|
$${z_1\over z_2}={z_1 z_2{}^*\over z_2z_2{}^*}\equiv{z_1 z_2{}^*\over|z_2|^2}$$
|
|
|
$(30)$ |
eine elegante Regel für die komplexe Division. Mit $z_1=1$ und $z_2=z=x+iy$ ergibt sich daraus die Formel
|
$${1\over z}={z^*\over zz^*}\equiv{z^*\over|z|^2}$$
|
|
|
$(31)$ |
| | | |

Betrag einer
reellen Zahl
| |
| | |
für den Kehrwert (den reziproken Wert oder die Inverse)
einer komplexen Zahl (den wir auch mit $z^{-1}$ bezeichnen können). Ein wichtiger Spezialfall ist $i^{-1}=-i$.
Die Menge aller komplexen Zahlen, deren Betrag gleich $1$ ist, bildet einen Kreis mit Radius $1$ und dem Ursprung als Mittelpunkt.
Er wird (komplexer) Einheitskreis genannt.
Wir sind jetzt in der Lage, komplexe Zahlen zu addieren, subtrahieren, multiplizieren und (außer durch $0$)
zu dividieren. Damit haben wir die Grundrechnungsarten von den reellen auf die komplexen Zahlen
übertragen. (In der Sprache der Mathematik haben wir die Menge $\mathbb{R}^2$ zu einem Körper
gemacht).
In den folgenden Abschnitten dieses Kapitels bekommen Sie einen kleinen Geschmack von der
Welt, die sich der Mathematik damit eröffnet.
|
| | |

Kehrwert einer
reellen Zahl

Körper
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Als erste Folge, die sich aus der Einführung der komplexen Zahlen ergibt, bemerken wir, dass manche Gleichungen, die innerhalb der
reellen Zahlen keine Lösung besitzen, komplexe Lösungen zulassen.
Insbesondere gilt das für alle quadratischen Gleichungen mit reellen Koeffizienten, d.h. Gleichungen der Form
wobei $p$ und $q$ gegebene reelle Zahlen sind. Wir nennen die Variable $z$, um anzudeuten, dass nun auch komplexe Lösungen gesucht werden.
Erinnern wir uns an die kleine Lösungsformel:
|
$$z_{1,2}=-{p\over 2}\pm\sqrt{{p2\over 4}-q}$$
|
. |
|
$(33)$ |
| | | |

kleine
Lösungsformel
| |
| | |
Ist der Ausdruck unter der Wurzel, also ${p^2\over 4}-q$, positiv, so gibt
es zwei reelle Lösungen. Ist er gleich $0$, so gibt es eine reelle Lösung. Ist er aber negativ, so gibt es keine
reelle Lösung. Werden nun auch komplexe Zahlen zugelassen, so ändert sich das Bild: Tritt beispielsweise in
(33) der Ausdruck $\pm\sqrt{-3}$ auf, so interpretieren wir ihn als $\pm i\sqrt{3}$. Wie sich leicht zeigen
lässt (siehe den nebenstehenden Button), stellt (33) auch dann die (einzigen) Lösungen
von (32) dar, wenn der Ausdruck unter der Wurzel negativ ist. Das bedeutet, dass jede
quadratische Gleichung mit reellen Koeffizienten zumindest eine komplexe Lösung besitzt (wobei "komplex" hier als
Spezialfall auch "reell" bedeuten kann – erinnern wir uns: auch reelle Zahlen sind komplexe Zahlen).
Die wichtigste derartige Gleichung ist
Sie ist gleichbedeutend mit (6), wobei wir hier die Variable nicht mit $x$, sondern mit $z$ bezeichnet haben.
Die kleine Lösungsformel führt auf die zwei Lösungen
|
$$z_{1,2}=0\pm\sqrt{-1}=\pm i$$
|
. |
|
$(35)$ |
Sie sind die einzigen Lösungen, da die kleine Lösungsformel alle Lösungen einer quadratischen Gleichung liefert.
Um das noch einmal ganz explizit zu überprüfen, setzen wir $z=x+iy$
in (34) ein und erhalten
| | | |
| |
| | |
Das ist genau dann erfüllt, wenn sowohl Real- als auch Imaginärteil der linken Seite verschwinden,
und das ist wiederum gleichbedeutend mit dem Gleichungssystem
|
\begin{eqnarray}
x^2-y^2+1&=&0\\
2xy&=&0
\end{eqnarray}
|
|
|
$(37)$ |
für das nun reelle Lösungen $(x,y)$ gesucht werden.
Die zweite Gleichung besagt, dass entweder $x$ oder $y$ gleich $0$ ist. Der Fall $y=0$ scheidet aus, da
die erste Gleichung dann $x^2+1=0$ lautet, was von keinem reellen $x$ erfüllt wird. Daher gilt $x=0$.
Die erste Gleichung wird damit zu $-y^2+1=0$ mit den beiden Lösungen $y=\pm 1$. Damit ist überprüft, dass
(34) tatsächlich genau zwei Lösungen besitzt, nämlich $-i$ und $i$.
(Ganz ähnlich wurde bei dem im obigen Button verstecken Beweis der kleinen Lösungsformel argumentiert).
Da wir (34) auch in der Form $z^2=-1$ schreiben können, stellt sich die Frage: Haben wir damit
die "Wurzel aus minus eins", also $\sqrt{-1}$ berechnet? Genau genommen gibt es die (Quadrat-)Wurzel aus $-1$ nicht,
sondern gleich zwei komplexe Zahlen, die diesen Anspruch erheben können, nämlich $-i$ und $i$.
Innerhalb der reellen Zahlen konnte das Wurzelziehen eindeutig gemacht werden, indem für jedes $x\geq 0$ festgelegt wurde,
dass $\sqrt{x}$ jene eindeutig bestimmte nichtnegative Zahl ist, deren Quadrat gleich $x$ ist.
Bei Quadratwurzeln aus negativen Zahlen funktioniert das nicht mehr. Die Zahlen $-i$ und $i$ sind als "Quadratwurzeln aus $-1$"
gewissermaßen "gleichberechtigt". Tritt beim Lösen einer quadratischen Gleichung in der Lösungsformel
(33) die Wurzel aus einer negativen Zahl auf, so sind damit dank des Doppelvorzeichens $\pm$ automatisch
beide Wurzeln gemeint. Das bedeutet übrigens, dass mit jeder komplexen Lösung auch ihre komplex Konjugierte eine
Lösung ist.
Wie werden weiter unten sehen, dass jede nichtverschwindende komplexe Zahl zwei
Quadratwurzeln besitzt.
Mit den komplexen Zahlen haben wir eine Erweiterung der Menge $\mathbb{R}$ gefunden, in der jede quadratische Gleichung
zumindest eine Lösung besitzt..
|
| | |

Gleichungssysteme
| |
| | |
| Geometrische Bedeutung der komplexen Addition |
| | | |
Zum Seitenanfang | |
| | |
Die geometrische Bedeutung der komplexen Addition sollte Ihnen bereits vertraut sein:
Da wir komplexe Zahlen mit reellen Zahlenpaaren identifizieren, können wir sie auch als zweidimensionale Vektoren ansehen.
Der algebraischen Definition der komponentenweisen Addition von reellen Zahlenpaaren entspricht das Aneinanderhängen
von Vektoren, wie es im ersten Vektorkapitel besprochen wurde. Auf diese Weise können wir
beispielsweise die Rechnung $(-1+i)+(2+i)=1+2i$ grafisch so darstellen:
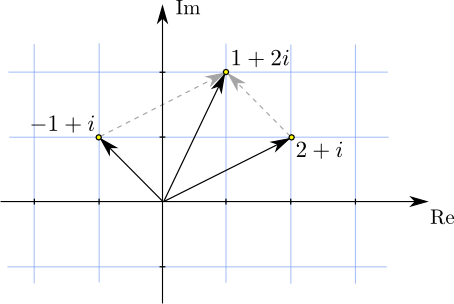
| | | |

geometrische Bedeutung der Summe zweier Vektoren
| |
| | |
Die komplexen Zahlen $-1+i$, $2+i$ und $1+2i$ entsprechen den drei gelb gekennzeichneten Punkten der komplexen Ebene.
Die schwarzen Pfeile stellen die Vektoren vom Ursprung zu diesen Punkten dar (also deren Ortsvektoren),
und die grau strichlierten Pfeile sind
verschobene Varianten der zu $-1+i$ und $2+i$ gehörenden Pfeile.
Die komplexe Addition stellt also weder rechnerisch noch geometrisch etwas Neues dar.
|
| | |

Ortsvektor
| |
| | |
| Geometrische Bedeutung der komplexen Multiplikation |
| | | |
Zum Seitenanfang | |
| | |
Besitzt die komplexe Multiplikation ebenfalls eine geometrische Deutung? Die Antwort lautet ja, und sie ist der Schlüssel
für die Bedeutung der komplexen Zahlen. Als Vorarbeit stellen wir komplexe Zahlen – also reelle Zahlenpaare –
in ebenen Polarkoordinaten dar.
Um den Punkt, durch den eine komplexe Zahl $z=x+iy$ in der komplexen Ebene dargestellt wird, anzugeben, kännen wir anstelle
von $x$ und $y$ auch dessen Abstand $r$ vom Ursprung und den im Gegenuhrzeigersinn gemessenen Winkel $\varphi$, den der Ortsvektor mit
der positiven reellen Achse einschließt, verwenden:

| | | |
| |
| | |
Wie im Kapitel über Winkelfunktionen besprochen, sind $x$ und $y$ dann durch die
Beziehungen
|
\begin{eqnarray}
x&=&r\cos\varphi\\
y&=&r\sin\varphi
\end{eqnarray}
|
|
|
$(38)$ |
festgelegt. $r$ heißt Radialkoordinate, $\varphi$ heißt Polarwinkel (oder Argument).
Eine komplexe Zahl $z=x+iy$ kann daher auch in der Form
|
$$z=r\left(\cos\varphi+i\sin\varphi\right)$$
|
|
|
$(39)$ |
angeschrieben werden. Wir nennen diese Form die Polardarstellung einer komplexen Zahl.
Die Radialkoordinate $r$ gibt dabei einfach den Betrag von $z$ an:
| | | |

ebene
Polarkoordinaten
| |
| | |
Das ist einerseits aufgrund der geometrischen Bedeutung von $r$ klar, folgt aber auch aus der Formel
(29) unter Zuhilfenahme der Identität $\sin^2\varphi+\cos^2\varphi=1$.
Die Radialkoordinate $r$ kann beliebige nichtnegative Werte annehmen. Der Polarwinkel $\varphi$ kann auf den
Bereich $0\leq\varphi<2\pi$ eingeschränkt werden oder – was manchmal praktischer ist –
kann beliebige reelle Werte annehmen, wobei aber $\varphi$ mit $\varphi+2\pi$ identifiziert wird.
Jetzt sind wir vorbereitet, nach der geometrischen Bedeutung der komplexen Multiplikation zu fragen.
Nehmen wir zwei komplexe Zahlen in Polardarstellung
|
\begin{eqnarray}
z_1&=&r_1\left(\cos\varphi_1+i\sin\varphi_1\right)\\
z_2&=&r_2\left(\cos\varphi_2+i\sin\varphi_2\right)
\end{eqnarray}
|
|
|
$(41)$ |
und multiplizieren sie:
|
\begin{eqnarray}
z_1z_2&=&r_1r_2\left(\cos\varphi_1+i\sin\varphi_1\right)\left(\cos\varphi_2+i\sin\varphi_2\right)=\\
&=&r_1r_2\left(\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin\varphi_2+\right.\\
&\qquad&\qquad\quad\left.+\,i\,
\left(\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\right)\right)
\end{eqnarray}
|
|
|
$(42)$ |
Die beiden Kombinationen von Winkelfunktionen, die hier auftreten, haben eine einfache Bedeutung:
|
\begin{eqnarray}
\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin\varphi_2&=&\cos\left(\varphi_1+\varphi_2\right)\\
\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2&=&\sin\left(\varphi_1+\varphi_2\right)
\end{eqnarray}
|
|
|
$(43)$
$(44)$ |
| | | |

Eigenschaften von Sinus und Cosinus
| |
| | |
Wir sind diesen Beziehungen (den so genannten Summensätzen) bereits im Kapitel über Winkelfunktionen begegnet
und werden weiter unten einen eleganten Beweis für sie finden.
Mit ihrer Hilfe können wir (42) zu
|
$$z_1z_2=r_1r_2\left(\cos\left(\varphi_1+\varphi_2\right)+i\sin\left(\varphi_1+\varphi_2\right)\right)$$
|
|
|
$(45)$ |
vereinfachen. Was hier vor uns haben, ist die Polardarstellung des Produkts $z_1z_2$.
Dessen Betrag ist gleich dem Produkt der Beträge $r_1r_2$, und sein Polarwinkel ist gleich der Summe der
Polarwinkel $\varphi_1+\varphi_2$. Daraus ergibt sich die geometrische Interpretation der komplexen
Multiplikation: Die Beträge werden multipliziert, die Polarwinkel werden addiert, wie die folgende
Skizze veranschaulicht:
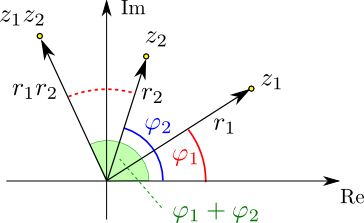
Um die Richtung zu ermitten, in die der Ortsvektor von $z_1z_2$ zeigt, wird der (rot strichlierte) Winkel $\varphi_1$ zu $\varphi_2$
addiert. Der Betrag von $z_1z_2$ wird als $r_1r_2$ berechnet und dann abgetragen.
Diese Darstellung erlaubt es uns, geometrisch zu verstehen, warum $i^2=-1$ ist:
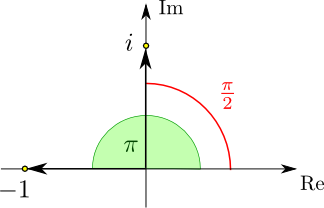
Der Polarwinkel von $i$ ist $\pi\over 2$. Der Polarwinkel von $i^2\equiv i\cdot i$ ist daher ${\pi\over 2}+{\pi\over 2}=\pi$.
Das ist aber gerade der Polarwinkel aller negativen reellen Zahlen. Da zudem $|i|=1$ gilt, ist der Betrag von
$i^2$ ebenfalls gleich $1$. Es folgt $i^2=-1$.
|
| | |

Summensätze
| |
| | |
| Mehr Gleichungen und Wurzeln |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Quadratwurzeln
Die geometrische Deutung der komplexen Multiplikation führt sofort zur Erkenntnis, dass jede
komplexe Zahl zwei Quadratwurzeln besitzt. Ist eine komplexe Zahl $z\neq 0$ mit Polarwinkel $\varphi$ gegeben, so sind diese
beiden Wurzeln jene komplexen Zahlen mit Betrag $\sqrt{|z|}$, die die Polarwinkeln ${\varphi\over 2}$ und ${\varphi\over 2}+\pi$ besitzen.
Die folgende Skizze illustriert diese Situation:
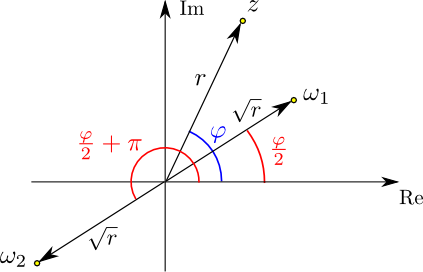
Die mit $\omega_1$ und $\omega_2$ bezeichneten komplexen Zahlen sind die beiden Quadratwurzeln aus $z$, d.h. sie
erfüllen $\omega_1{}^2=\omega_2{}^2=z$. (Der Polarwinkel von $\omega_2{}^2$ ergibt sich zunächst als
$2({\varphi\over 2}+\pi)=\varphi+2\pi$, was aber mit $\varphi$ identifiziert wird).
Die beiden Wurzeln unterscheiden sich nur durch ihr Vorzeichen, d.h. es gilt $\omega_2=-\omega_1$.
Aufgrund dieser Mehrdeutigkeit beim komplexen Wurzelziehen sollte das Symbol $\sqrt{z}$ nur mit Vorsicht eingesetzt werden,
wenn ${\rm Im}(z)\neq 0$ ist. Genau genommen bezeichnet es zwei Zahlen.
| | | |
| |
| | |
Höhere Wurzeln
Auf analoge Weise können die $n$-ten Wurzeln beliebiger komplexer Zahlen gebildet werden.
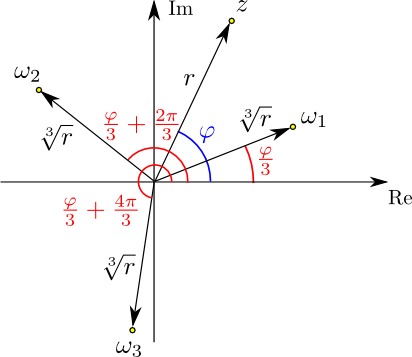
Jede komplexe Zahl $z\neq 0$ besitzt $n$ (komplexe) $n$-te Wurzeln. Die folgende Skizze illustriert das für den
Fall $n=3$:
| | | |
| |
| | |
Überlegen Sie selbst, warum $\omega_1{}^3=\omega_2{}^3=\omega_3{}^3=z$ gilt (und klicken Sie danach auf den
nebenstehenen Button)!
Die $n$-ten Wurzeln der Zahl $1$ liegen alle am Einheitskreis. $1$ selbst ist natürlich so eine Wurzel. Die anderen werden
durch schrittweise Erhöhung des Polarwinkels um $2\pi\over n$ erhalten, wie die folgende Skizze für $n=2$, $3$ und $4$ zeigt:

Diese $n$-tenWurzeln aus $1$ werden "$n$-te Einheitswurzeln" genannt.
So gibt es beispielsweise eine reelle "dritte Einheitswurzel", nämlich $\omega_1=1$. Die beiden anderen
"dritten Einheitswurzeln" sind durch
|
\begin{eqnarray}
\omega_2&=&\cos\left(2\pi\over 3\right)+i\sin\left(2\pi\over 3\right)={-1+i\sqrt{3}\over 2}\\
\omega_3&=&\cos\left(4\pi\over 3\right)+i\sin\left(4\pi\over 3\right)={-1-i\sqrt{3}\over 2}
\end{eqnarray}
|
|
|
$(46)$ |
gegeben. Überprüfen Sie selbst durch eine Rechnung, dass $\omega_2{}^3=\omega_3{}^3=1$ gilt!
Die "$n$-ten Wurzeln aus $-1$" sind ebenfalls regelmässig am Einheitskreis angeordnet, nur in einem
anderen Muster, wie die folgende Skizze für $n=2$, $3$ und $4$ zeigt:

Insbesondere besitzt $-1$ nur dann eine reelle $n$-te Wurzel, wenn $n$ ungerade ist. Im Rahmen der reellen Zahlen ist $\sqrt[\large 3\,]{-1}=-1$,
aber $\sqrt[\large 4\,]{-1}$ macht im Reellen ebensowenig Sinn wie $\sqrt{-1}$. Das Gleiche gilt auch für andere
negative Zahlen.
| | | |
| |
| | |
Gleichungen dritter Ordnung
Dieser Unter-Abschnitt kann von
''EinsteigerInnen'' ausgelassen oder nur kurz überflogen werden.
Wir erwähnen nun eine Anwendung der kompexen Zahlen, die für reelle Probleme relevant ist.
Eine Gleichung dritter Ordnung (kubische Gleichung) mit reellen Koeffizienten
besitzt zumindest eine reelle Lösung, maximal aber drei.
Falls eine Lösung bekannt ist, so sind auch die anderen in Reichweite, aber wie kommt man zu dieser einen
(außer sie zu erraten, wie es bei Mathematikaufgaben in der Schule oft möglich ist)?
Gleichungen höherer Ordnung haben die Mathematik in ihrer Entwicklung seit langer Zeit
interessiert. Gibt es für sie "Lösungsformeln" analog zu jener für die quadratischen Gleichungen?
Bereits im 16. Jahrhundert fand Gerolamo Cardano (genannt Cardanus) eine exakte Lösungsmethode für kubische Gleichungen.
Etwas verstörend daran war, dass sie erforderte, Wurzeln aus negativen Zahlen zu ziehen. Wenn man das aber ignorierte
und einfach weiterrechnete, so ergaben sich am Ende Lösungen, von denen
zumindest eine reell war. Um das zu illustrieren, beschränken wir uns auf eine kubische Gleichung
ohne quadratischen Term und schreiben sie in der Form
an, wobei $a$ und $b$ gegebene reelle Zahlen sind. Wir wollen Cardanos Methode hier nicht beweisen, sondern nur
skizzieren. Sie läuft darauf hinaus, den Ausdruck
|
$$x=\sqrt[\Large 3\,\,]{b+\sqrt{a^3+b^2}}+\sqrt[\Large 3\,\,]{b-\sqrt{a^3+b^2}}$$
|
|
|
$(48)$ |
zu berechnen. Was bedeutet er? Ist $a^3+b^2<0$, so können wir $\sqrt{a^3+b^2}$ als imaginäre Zahl
interpretieren. Damit wären in (48) die dritten Wurzeln aus zwei komplexen Zahlen zu bilden!
Sehen wir uns das anhand des Beispiels $a=-7$ und $b=10$ an: Die Gleichung (47) lautet dann $x^3-21x-20=0$, und
mit $a^3+b^2=-243$ führt (48) zunächst auf
|
$$x=\sqrt[\Large 3\,\,]{10+\sqrt{-243}}+\sqrt[\Large 3\,\,]{10-\sqrt{-243}}$$
|
. |
|
$(49)$ |
Wir interpretieren das als
|
$$x=\sqrt[\Large 3\,\,]{10+i\sqrt{243}}+\sqrt[\Large 3\,\,]{10-i\sqrt{243}}$$
|
|
|
$(50)$ |
(wobei die Mehrdeutigkeit der Quadratwurzel hier insofern als nicht sehr gravierend erscheint, als wir die Summe
über zwei Terme bilden, in denen jeweils eine der beiden Wurzeln $i\sqrt{243}$ und $-i\sqrt{243}$ auftritt).
Nun müssen wir die dritten Wurzeln ziehen. Wieder tritt eine Mehrdeutigkeit auf, denn jede komplexe Zahl $\neq 0$
besitzt drei dritte Wurzeln! Welche sollen wir wählen? Dazu bemerken wir, dass
$10+i\sqrt{243}$ und $10-i\sqrt{243}$ zueinander komplex konjugiert sind. Geometrisch bedeutet das, dass sie in der komplexen Ebene
durch eine Spiegelung an der reellen Achse auseinander hervorgehen. Wir wählen nun die beiden dritten Wurzeln
in (50) so, dass sie zueinander komplex konjugiert sind. Es gibt drei Möglichkeiten, das zu tun. In allen drei Fällen stellt
(50) eine Summe zweier zueinander komplex konjugierter Zahlen dar. Eine solche Summe ist immer
reell (da die Imaginärteile einander genau aufheben). Auf diese Weise bekommen wir
alle drei Lösungen der gegebenen Gleichung, nämlich $-4$, $-1$ und $5$!
Diese Methode funktioniert ganz allgemein, sofern $a^3+b^2<0$ ist. Gilt $a^3+b^2\geq 0$, so gibt es nur eine einzige
reelle Lösung, die mit (48) ganz im Rahmen der reellen Zahlen ermittelt werden kann. Falls $a^3+b^2=0$,
so gibt es entweder eine einfache und eine doppelte reelle Lösung oder eine dreifache reelle Lösung.
Dabei sei allerdings hinzugefügt, dass die Berechnung verschachtelter Wurzeln, wie sie hier auftreten, nicht leicht ist.
Dennoch ist Cardanos Methode eine exakte, die systematisch angewandt werden kann, analog zur kleinen Lösungsformel
für quadratische Gleichungen.
Cardanos Entdeckung, dass mit Wurzeln aus negativen Zahlen gerechnet werden kann, und dass damit
reelle Probleme gelöst werden können, war die Geburtsstunde der komplexen Zahlen.
| | | |

Funktionen und Gleichungen dritter Ordnung
| |
| | |
Der Fundamentalsatz der Algebra
Eine der wichtigsten Eigenschaften der komplexen Zahlen wurde von Carl Friedrich Gauß im Jahr 1799 entdeckt und in Form des
Fundamentalsatzes der Algebra bewiesen. Dieses Theorem besagt, dass jede algebraische Gleichung,
also jede Gleichung der Form $f(x)=0$, wobei $f$ ein Polynom vom Grad $\geq 1$ mit beliebigen komplexen
Koeffizienten ist, zumindest eine komplexe Lösung besitzt.
Eine unmittelbare Folge dieses Satzes ist, das jedes derartige Polynom in Linearfaktoren zerlegt werden kann,
die die Lösungen der entsprechenden Gleichung unmittelbar anzeigen.
Für quadratische Gleichungen können wir diese Eigenschaften leicht nachvollziehen:
Eine quadratische Gleichung der Form (32) mit beliebigen komplexen Koeffizienten $p$ und $q$ besitzt zwei
durch die kleine Lösungsformel (33) angegebene Lösungen (die auch zusammenfallen können),
wobei die Wurzel im komplexen Sinn interpretiert wird. (Sie steht, wie wir bereits wissen, für zwei Zahlen, was durch das
Doppelvorzeichen $\pm$ ausgedrückt wird). Der Beweis funktioniert ganz analog zu dem im Kapitel Gleichungen
im reellen Kontext geführten. Die Zerlegung in Linearfaktoren
|
$$z^2+pz+q=(z-z_1)(z-z_2)$$
|
|
|
$(51)$ |
wird durch den Satz von Vieta sichergestellt und kann ebenfalls leicht nachgerechnet werden.
Der Fundamentalsatz der Algebra besagt, dass das auch für Gleichungen höherer Ordnung gilt
(mit einer entsprechend höheren Anzahl von Lösungen und Linearfaktoren).
|
| | |

Algebraische Gleichungen
(in Vorbereitung)

Zerlegung in Linearfaktoren und der Vietasche Satz im Reellen
| |
| | |
| Komplexe Exponentialfunktion |
| | | |
Zum Seitenanfang | |
| | |
Wenn Sie die Multiplikationsregel in Polarkoordinaten (45) anschauen, wird ihnen vielleicht auffallen, dass sie
eine Eigenschaft mit der Exponentialfunktion gemeinsam hat: Der Polarwinkel des Produkts zweier komplexer Zahlen ist die
Summe (nicht das Produkt!) der Polarwinkel dieser Zahlen. Mit der für die reelle Exponentialfunktion geltenden
Identität
(wobei $a$ und $b$ reelle Zahlen sind)
verhält es sich ähnlich: Der Exponent des Produkts zweier Potenzen ist die Summe (nicht das Produkt!)
der Exponenten dieser Potenzen. Diese Ähnlichkeit könnte es fast vermuten lassen, dass eine komplexe Zahl
in irgend einem Sinn exponentiell von ihrem Polarwinkel $\varphi$ abhängt. Und tatsächlich ist das der Fall!
Gestärkt durch die Aussicht auf eine weitere Entdeckung, überlegen wir, ob und wie die Exponentialfunktion auf komplexe Zahlen
angewandt werden kann. Dabei beschränken wir uns vorerst auf imaginäre Zahlen. Wir fragen, ob es einen Sinn macht,
$e^{iu}$ für eine reelle Zahl $u$ zu bilden.
Die einfachste Methode, dies zu tun, benutzt die Taylorreihe der Exponentialfunktion
|
$$e^x=\sum_{n=0}^\infty{x^n\over n!}\equiv 1+x+{x^2\over 2!}+{x^3\over 3!}+{x^4\over 4!}+\dots$$
|
|
|
$(53)$ |
Diese Reihe gilt zunächst für reelle $x$, aber wir definieren $e^{iu}$ für jede reelle Zahl $u$
durch den Wert der Reihe, wenn $iu$ anstelle von $x$ eingesetzt wird. Unter Ausnutzung von $i^2=-1$ (und daher
$i^3=-i$, $i^4=1$, $i^5=i$ usw.) erhalten wir eine Reihe, die wir sofort in Real- und Imaginärteil
trennen können:
|
\begin{eqnarray}
e^{iu}&=&\sum_{n=0}^\infty{i^n u^n\over n!}\equiv 1+iu-{u^2\over 2!}-i{u^3\over 3!}+{u^4\over 4!}+\dots=\\
&=&1-{u^2\over 2!}+{u^4\over 4!}-{u^6\over 6!}+\dots\\
&\qquad& +\,i\,\left(u-{u^3\over 3!}+{u^5\over 5!}-{u^7\over 7!}+\dots\right)
\end{eqnarray}
|
|
|
$(54)$ |
Die beiden Reihen, die hier als Real- und Imaginärteil auftreten, sind genau die Taylorreihen dor Cosinus- und der
Sinusfunktion:
|
\begin{eqnarray}
\cos u&=&1-{u^2\over 2!}+{u^4\over 4!}-{u^6\over 6!}+\dots\\
\sin u&=& u-{u^3\over 3!}+{u^5\over 5!}-{u^7\over 7!}+\dots
\end{eqnarray}
|
|
|
$(55)$
$(56)$ |
Auf diese Weise erhalten wir die so genannte Eulersche Formel
|
$$e^{iu}=\cos u+i\sin u$$
|
. |
|
$(57)$ |
Sie zählt zu den wichtigsten mathematischen Beziehungen überhaupt, führt auf
eine Fülle neuer Erkenntnisse und ist die Grundlage zahlreicher rechentechischer Vereinfachungen.
Wie unmittelbar mit den hier auftretenden Reihen nachgerechnet werden kann, gilt für alle reellen
Zahlen $u_1$ und $u_2$ die Identität
|
$$e^{iu_1}e^{iu_2}=e^{i(u_1+u_2)}$$
|
. |
|
$(58)$ |
Die Exponentialfunktion kann durch die Definition
|
$$e^{x+iy}=e^x e^{iy}\equiv e^x(\cos y+i\sin y)$$
|
|
|
$(59)$ |
auf beliebige komplexe Zahlen ausgedehnt werden. Sie erfüllt dann
(52) für beliebige komplexe Zahlen $a$ und $b$. Mit
werden Potenzen mit beliebigen positiven reellen Basen und komplexen Exponenten definiert.
(Auch eine Erweiterung auf komplexe Basen ist möglich, aber nicht eindeutig. Wir
gehen darauf nicht weiter ein).
| | | |

Potenzen mit reellen Exponenten

Taylorreihe der Exponentialfunktion

Taylorreihen von
Sinus und Cosinus
| |
| | |
Noch einmal Polardarstellung
Der Vergleich von (57) mit (39) führt sofort auf
das weitere Ergebnis, dass die Polardarstellung einer komplexen Zahl auch in der Form
geschrieben werden kann. Aus ihr folgt mit (58) sofort die Multiplikationsregel (45) in der Form
|
$$z_1z_1=r_1r_2 e^{i\varphi_1}e^{i\varphi_2}=r_1r_2 e^{i(\varphi_1+\varphi_2)}$$
|
, |
|
$(61)$ |
womit ihr tieferer Grund – die Verwandtschaft der Exponentialfunktion mit den Winkelfunktionen, die sich nur im Komplexen zeigt –
aufgeklärt ist.
| | | |
| |
| | |
Beweis der Summensätze
Auch die Summensätze (Additionstheoreme) (43) und (44)
für die Cosinus- und die Sinusfunktion können nun auf elegante Weise bewiesen werden:
Sie sind nichts anderes als Real- und der Imaginärteil der Beziehung (58): Multiplizieren wir
$e^{i\varphi_1}=\cos\varphi_1+i\sin\varphi_1$ mit $e^{i\varphi_2}=\cos\varphi_2+i\sin\varphi_2$ und multiplizieren aus,
so erhalten wir
|
\begin{eqnarray}
&&\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin\varphi_2\\
&&\,\,\,+\,\,i\,\,\left(
\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\right)
\end{eqnarray}
|
|
|
$(62)$ |
Andererseits ist $e^{i\varphi_1}e^{i\varphi_2}$ mit (58) gleich $e^{i(\varphi_1+\varphi_2)}$, also
|
$$\cos\left(\varphi_1+\varphi_2\right)+i\,\sin\left(\varphi_1+\varphi_2\right)$$
|
. |
|
$(63)$ |
Durch Vergleich der Real- und Imaginärteile ergeben sich genau die Beziehungen
(43) und (44).
| | | |
| |
| | |
Die schönste Formel der Welt
Für $u=\pi$ reduziert sich die Eulersche Formel (57) auf $e^{i\pi}=-1$, was in der Form
als die "schönste Formel der Welt" gefeiert wurde:
Sie setzt die wichtigsten mathematischen Dinge – die Eulersche Zahl $e$, die imaginäre Einheit $i$,
die Kreiszahl $\pi$, die Addition $+$, die Einheit $1$, die Gleichheit $=$ und die Null – in eine bemerkenswerte
Beziehung.
| | | |
| |
| | |
Physikalische Anwendungen
Die komplexe Exponentialfunktion leistet nicht nur in der Mathematik, sondern auch
in anderen Gebieten, insbesondere der Physik, nützliche Dienste.
Besonders wichtig ist die Beobachtung, dass alle komplexen Zahlen mit festgehaltenem Betrag
$r$ auf einem Kreis mit Radius $r$ um den Ursprung liegen. Lassen wir den Polarwinkel
gemäß $\varphi=\omega t$ (mit einer reellen Konstante $\omega$, der
Winkelgeschwindigkeit oder Kreisfrequenz) proportional zur Zeit $t$ anwachsen,
so beschreibt
eine gleichmäßige Kreisbewegung (mit Radius $r$). Die Projektion dieser Bewegung auf die
reelle Achse, also
|
$$x(t)= {\rm Re}(r e^{i\omega t})\equiv r\cos(\omega t)$$
|
|
|
$(66)$ |
beschreibt eine harmonische Schwingung (mit Amplitude $r$).
Eine Phasenverschiebung $\phi$ kann in der Form
|
$$x(t)= {\rm Re}(r e^{i(\omega t+\phi)})\equiv r \cos(\omega t+\phi)$$
|
|
|
$(67)$ |
hinzugenommen werden, eine Dämpfung (mit Dämpfungskoeffizient $D$)
in der Form
|
$$x(t)= {\rm Re}(r e^{(-D+i\omega)t})\equiv r e^{-Dt}\cos(\omega t)$$
|
. |
|
$(68)$ |
Diese Sachverhalte spielen in der Physik eine wichtige Rolle.
Oft ist es möglich, mit komplexen Größen zu rechnen, die Einfachheit der
Exponentialfunktion (hinsichtlich Multiplikation, aber auch hinsichtlich ihrer Ableitung)
auszunutzen und erst zum Schluss, wenn es etwa um die Vorhersage beobachtbarer Größen
geht, durch Bilden des Realteils wieder ins Reelle zurückzukehren. Beispielsweise ist der
Wechselstromwiderstand eine in der Elektrotechnik genutzte komplexe Hilfsgröße,
die genau auf den hier besprochenen Beziehungen beruht.
|
| | |
| |
| | |
| Einige Stichworte zur komplexen Analysis |
| | | |
Zum Seitenanfang | |
| | |
Dieser Abschnitt kann von
''EinsteigerInnen'' ausgelassen werden.
Was Sie bisher unter den Schlagworten Differenzieren und Integrieren kennen gelernt haben, hat sich (wahrscheinlich)
ganz im Reellen abgespielt. Im mathematischen Gebiet der komplexen Analysis (oder Funktionentheorie) werden diese Konzepte auf die
komplexen Zahlen übertragen. Dabei wird von Funktionen ausgegangen, die komplexe Zahlen in komplexe Zahlen
überführen, also von Funktionen der Form
$f:\mathbb{C}\rightarrow \mathbb{C}$ oder $f:G\rightarrow \mathbb{C}$, wobei $G$ eine Teilmenge von $\mathbb{C}$ ist.
Eine Funktion, die komplexe Zahlen in komplexe Zahlen überführt, also $z\mapsto f(z)$, heißt im Punkt
$z_0$ (im komplexen Sinn) differenzierbar, wenn – analog zum reellen Ableitungsbegriff – der Grenzwert
|
$$f'(z_0)=\lim_{z\rightarrow z_0}{f(z)-f(z_0)\over z-z_0}$$
|
|
|
$(69)$ |
existiert. Beachten Sie, dass $z-z_0$ komplex ist und daher hier eine Division im komplexen Sinn vorliegt und nicht einfach eine
Division durch den Abstand zweier Punkte.
Sie ist der Grund für viele bemerkenswerte Eigenschaften komplex-differenzierbarer Funktionen.
So sind Real- und Imaginärteil einer solchen Funktion nicht voneinander unabhängig,
und eine differenzierbare Funktion ist automatisch beliebig oft differenzierbar!
Ist eine Funktion in allen Punkten eines Gebiets differenzierbar, so lässt sie sich
lokal, d.h. innerhalb eines Kreises um jeden gegebenen Punkt $z_0$ dieses Gebiets, in eine Potenzreihe
|
$$f(z)=\sum_{n=0}^\infty a_n(z-z_0)^n$$
|
|
|
$(70)$ |
entwickeln und wird analytisch genannt. Im Gegensatz zu reellen Funktionen reicht im Komplexen die Differenzierbarbeit
für die Existenz einer Potenzreihenentwicklung aus. Beispiele für analytische Funktionen sind
Polynome und die komplexe Exponentialfunktion. Auch viele andere aus dem reellen Kontext bekannten Funktionen
(wie Potenzen, Winkelfunktionen und der Logarithmus) lassen sich – zumindest lokal –
"analytisch ins Komplexe fortsetzen".
| | | |

Ableitung
im Reellen

Grenzwerte reeller Funktionen

Potenzreihen
| |
| | |
Das komplexe Integral benötigt zunächst eine Kurve $\gamma$ in der komplexen Ebene.
Ist sie in Parameterdarstellung $t\mapsto z(t)$ mit $t_0\leq t\leq t_1$ gegeben, so wird
|
$$\int_\gamma f(z)dz=\int_{t_0}^{t_1}f(z(t)){dz(t)\over dt}dt$$
|
|
|
$(71)$ |
definiert, was von der gewählten Parameterdarstellung unabhängig ist. Ist $f$ analytisch in einem Gebiet $G$,
innerhalb dessen sich jede geschlossene Kurve auf einen Punkt zusammenziehen
lässt, so ist das komplexe Integral über eine geschlossene Kurve, die ganz in $G$ liegt, gleich $0$.
Diese Eigenschaft (der Cauchysche Integralsatz) kann dazu ausgenutzt werden, um gewisse Integrale (auch relle Integrale!)
"ohne Integration" zu berechnen, sondern lediglich durch eine Untersuchung des Verhaltens des Integranden
in der Nähe einzelner Punkte (Residuensatz).
Die komplexe Analysis bietet einen unerschöpflichen Reichtum an Methoden, die in praktisch allen Gebieten der
Mathematik und in etlichen anderen Wissenschaften (auch zur Lösung von Problemen, die ganz im Reellen gestellt sind)
Anwendung finden.
|
| | |

Integral im Reellen

Parameterdarstellung einer Kurve
(in Vorbereitung)
| |