| | |
| | | |
| |
| | |
| | | |
| |
| | |
| | | |
| |
| | |
Vorgeschmack
Haben Sie sich schon einmal gefragt, wie ein Taschenrechner oder ein Computerprogramm
Wurzeln, Winkelfunktonen, Exponentialfunktionen und Logarithmen berechnet?
Im Zuge Ihrer bisherigen Mathematikausbildung ist Ihnen vielleicht aufgefallen, dass immer wieder neue Zahlen und
Funktionen eingeführt werden, die mit den bis dahin gelernten Rechenoperationen und Methoden nicht berechnet werden
können:
| | | |
| |
| | |
- Zuerst lernen wir die Grundrechnungsarten addieren, subtrahieren, multiplizieren und dividieren, und zwar zuerst mit ganzen Zahlen,
dann mit Zahlen, die durch eine (abbrechende oder periodische) Dezimaldarstellung angeschrieben werden können und daher alle rational sind.
- Irgendwann tauchen die ersten Quadratwurzeln auf, und mit ihnen das Problem, dass beispielsweise $\sqrt{2}$
(eine irrationale Zahl) nicht durch ein einfaches Hintereinanderausführen von Grundrechnungsarten mit ganzen Zahlen berechnet werden kann.
Es gibt zwar eine "händische" Methode des Wurzelziehens (die ein bisschen komplizierter als das händische Dividieren ist),
aber die wird heute kaum noch gelernt.
Eine Zahl wie $\sqrt{2}$ zu berechnen, wird an den Rechner delegiert – der gibt sehr effizient, je nach der Zahl
der Dezimalstellen, mit denen er operiert, einen Näherungswert wie 1.41421356 oder 1.414213562373 aus.
- Die einfachen Ideen des Quadrierens und Wurzelziehens werden zum Potenzieren mit beliebigen reellen Zahlen
verallgemeinert. Rechner haben offenbar kein Problem mit Eingaben wie $26^{-1/5}$, $\pi^{\sqrt{2}}$ oder $e^{-1/2}$.
Ebenso wie die meisten Quadratwurzeln können auch Zahlen dieser Art – abgesehen von Ausnahmefällen wie $27^{1/3}$ –
nicht durch die Grundrechnungsarten ausgedrückt werden.
- Früh im Mathematikunterricht tritt auch die Kreiszahl $\pi$ auf. Trotz ihrer Wichtigkeit lässt sie sich
nicht durch eine einfache "Formel" ausdrücken, in der nur die bis dahin gelernten Operationen (Grundrechnungsarten und Potenzen) vorkommen.
- Der Übergang zu Exponentialfunktionen, d.h. zu Potenzen, in denen der Exponent als Variable aufgefasst wird
(wie $x\mapsto 2^x$ oder $x\mapsto e^x$ mit der Eulerschen Zahl $e$ als Basis) ist mathematisch äußerst furchtbar.
Hier werden im Mathematikunterricht oft die ersten Hinweise auf eine konkrete Berechnung gegeben: $e$ und $e^x$ als Grenzwert einer Folge oder
als Wert einer Reihe.
- Zu den Exponentialfunktionen gesellen sich deren Umkehrfunktionen, die Logarithmen (allen voran der natürliche Logarithmus
$x\mapsto \ln x$), aber die grundsätzliche Frage, wie ihre Funktionswerte konkret mit beliebiger Genauigkeit berechnet werden können,
bleibt vorerst offen. In der Praxis erledigt das wieder der Rechner.
- Schließlich kommen irgendwann die Winkelfunktionen Sinus, Cosinus und Tangens (vielleicht aus Cotangens) dazu. Auch diese lassen sich
– von Ausnahmen wie $\sin({\pi\over 4})={1\over\sqrt{2}}$ oder $\cos({\pi\over 3})={1\over 2}$ abgesehen – nicht
auf die bis dahin gelernten Operationen und Funktionen
(Grundrechnungsarten, Potenzen, Exponentialfunktionen und Logarithmen) zurückführen.
- Auch in weiterer Folge hält die Mathematik zahlreiche derartige Neuschöpfungen bereit, die sich nicht durch
die bis dahin bekannten Operationen und Funktionen ausdrücken lassen.
Potenzreihen bieten für alle diese Probleme eine mögliche Lösung – mit ihrer Hilfe können
die meisten Zahlen und Funktionen, die Ihnen bisher begegnet sind, auf systematische Weise numerisch beliebig genau angenähert werden.
Sie stellen eine ganz neue Möglichkeit dar, funktionale Abhängigkeiten zu beschreiben und mathemathische Probleme zu lösen
– als praktische Werkzeuge sind sie aus den Naturwissenschaften und den technischen Wissenschaften nicht
wegzudenken.
| | | |

rationale Zahlen
irrationale Zahlen

Potenzen

Exponential- und
Logarithmus-
funktionen

Folgen
Reihen

Winkelfunktionen
| |
| | |
Eine erstaunliche Eigenschaft von Polynomen
Wir beginnen unsere Betrachtungen mit Polynomfunktionen. Polynomfunktionen (kurz Polynome) bilden eine recht einfache Klasse von Funktionen.
Ein Beispiel eines Polynoms dritten Grades ist
Lassen Sie sich von der Reihenfolge, in der wir die einzelnen Summanden hingeschrieben haben, nicht verwirren: Sie können diese
Funktionsdefinition ebensogut in der Form $f(x)=7x^3-5x^2+9x+3$ anschreiben. Es wird sich jedoch gleich zeigen, dass die obige Form
für die Zwecke dieses Kapitels bequemer ist. In (1) bezeichnet $x$ eine reelle Variable, d.h. $f$ ist eine Funktion,
die jeder reellen Zahl $x$ eine reelle Zahl $f(x)$ zuordnet. Um den Funktionswert $f(x)$ für ein gegebenes $x$ zu berechnen,
also beispielsweise $f(-4)$ oder $f(\pi^2)$, müssen lediglich reelle Zahlen addiert, subtrahiert und multipliziert werden.
(1) heißt Polynom dritten Grades, weil $3$ der größte auftretende Exponent der Variable $x$ ist.
Ganz allgemein ist eine Polynomfunktion dritten Grades eine Funktion der Form
|
$f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3$
|
, |
|
$(2)$ |
wobei die Koeffizienten $a_0$, $a_1$, $a_2$ und $a_3$ vorgegebene reelle Zahlen sind. Sie bestimmen $f$ eindeutig.
Im Beispiel (1) ist $a_0=3$, $a_1=9$, $a_2=-5$ und $a_3=7$.
| | | |

Polynome

Polynomfunktionen
| |
| | |
Nun wollen wir ein bisschen differenzieren und alle Ableitungen der Funktion (1) berechnen: die erste, die zweite,
die dritte usw. Wir beginnen mit der Funktionsgleichung selbst und differenzieren:
|
$\begin{eqnarray}
f(x)&=&3+9\,x-5\,x^2+7\,x^3\\
f'(x)&=&9\cdot 1-5\cdot 2\,x+7\cdot 3\,x^2\\
f''(x)&=&-5\cdot 2\cdot 1 +7\cdot 3\cdot 2\,x\\
f'''(x)&=&7\cdot 3\cdot 2\cdot 1\\
f''''(x)&=&0\\
f'''''(x)&=&0
\end{eqnarray}$
|
|
|
$(3)$ |
| | | |

Differenzieren
| |
| | |
Dabei haben wir uns strikt an die Ableitungsregel $(x^n)'=n\,x^{n-1}$ gehalten und auch die Einser, die aus $(x)'=1$ entstehen,
hingeschrieben. Mit (3) haben wir alle Ableitungen (beliebig hoher Ordnung) von $f$ berechnet –
ab der vierten sind sie alle gleich $0$. Nun setzen wir in diese Beziehungen $x=0$ ein, d.h. wir
berechnen den Wert der Funktion und die Werte alle Ableitungen an der Stelle $0$:
|
$\begin{eqnarray}
f(0)&=&3\\
f'(0)&=&9\cdot 1\\
f''(0)&=&-5\cdot 2\cdot 1\\
f'''(0)&=&7\cdot 3\cdot 2\cdot 1\\
f''''(0)&=&0\\
f'''''(0)&=&0
\end{eqnarray}$
|
|
|
$(4)$ |
Alle Ableitungen von höherer Ordnung als drei sind an der Stelle $0$ gleich $0$.
Erkennen Sie ein Muster?
- $f(0)$ ist gleich dem ersten Koeffizienten $3$, der in (1) ohne $x$ auftritt.
- $f'(0)$ ist gleich dem Koeffizienten von $x$ in (1), also $9$, multipliziert mit $1\equiv 1!$.
- $f''(0)$ ist gleich dem Koeffizienten von $x^2$ in (1), also $-5$, multipliziert mit $2\cdot 1\equiv 2!$.
- $f'''(0)$ ist gleich dem Koeffizienten von $x^3$ in (1), also $7$, multipliziert mit $3\cdot 2\cdot 1\equiv 3!$.
- $f''''(0)$ ist gleich $0$, da in (1) kein $x^4$ auftritt.
- $f'''''(0)$ ist gleich $0$, da in (1) kein $x^5$ auftritt.
- usw.
| | | |

Ableitung von
Potenzfunktionen
| |
| | |
Dabei haben wir die Schreibweise $n!$ für "$n$ Faktorielle", also für $n(n-1)(n-2)\dots 3\cdot 2\cdot 1$ verwendet.
Diese Produkte aufeinanderfolgender natürlicher Zahlen sind durch die wiederholte Anwendung der Ableitungsregel für Potenzen entstanden,
wie beispielsweise in
$x^3$ $-$ableiten$\rightarrow$ $3\,x^2$
$-$ableiten$\rightarrow$ $3\cdot 2\,x$
$-$ableiten$\rightarrow$ $3\cdot 2\cdot 1$.
Führen wir die gleiche Prozedur mit dem allgemeinen Polynom (2) durch, so erhalten wir auf genau die gleiche
Weise
|
$\begin{eqnarray}
f(0)&=&a_0 &=& a_0\cdot 0!\\
f'(0)&=&a_1\cdot 1 &=& a_1\cdot 1!\\
f''(0)&=&a_2\cdot 2\cdot 1 &=& a_2\cdot 2!\\
f'''(0)&=&a_3\cdot 3\cdot 2\cdot 1 &=& a_3\cdot 3!\\
f''''(0)&=&0\\
f'''''(0)&=&0
\end{eqnarray}$
|
|
|
$(5)$ |
Um das Muster noch schöner hervortreten zu lassen, haben wir in der ersten Zeile $a_0$ mit $0!$ multipliziert, was wir wegen
$0!=1$ dürfen. Wir erkennen daran:
- Die vier Koeffizienten eines Polynoms dritter Ordnung können durch den Funktionswert (den wir auch die "nullte Ableitung"
nennen) und die Ableitungen bis zur dritten Ordnung ausgedrückt werden.
- Die konkrete Form der erhaltenen Beziehung entbehrt nicht einer gewissen Schönheit:
Bezeichnen wir die $n$-te Ableitung von $f$ mit $f^{(n)}$, also etwa $f^{(3)}(x)\equiv f'''(x)$,
und schreiben $f$ selbst als $f^{(0)}$ (nullte Ableitung), so gilt
|
$f^{(n)}(0)=a_n\,n!$ und daher $a_n={\Large f^{(n)}(0)\over \Large n!}$
|
|
|
$(6)$ |
für $n=0,1,2$ und $3$. Damit haben wir mit einem Schlag alle Koeffizienten eines
beliebigen Polynoms dritten Ordnung durch die Werte aller Ableitungen (einschließlich der nullten)
an der Stelle $0$ ausgedrückt.
- Das bedeutet erstaunlicherweise, dass ein Polynom dritten Grades durch die vier Größen
$f(0)$, $f'(0)$, $f^{(2)}(0)$ und $f^{(3)}(0)$, die ja alle nur das Verhalten in einer kleinen Umgebung des Punktes $0$
betreffen, eindeutig bestimmt ist. Sind diese vier Größen vorgegeben, so ist damit der Funktionswert $f(x)$ für
jede reelle Zahl $x$ eindeutig festgelegt!
Dieses Ergebnis ist nicht auf Polynome dritten Grades beschränkt. Tatsächlich lässt sich unsere Argumentation
für Polynome beliebigen Grades wiederholen. Die $n$-te Ableitung an der Stelle $0$, also $f^{(n)}(0)$,
ist dann immer gleich $a_n$, dem Koeffizienten von $x^n$, multipliziert mit $n!$. Mit anderen Worten: Es gilt dann stets
(6), für alle $n$ von $0$ bis zum Grad des Polynoms. Und wenn wir vereinbaren,
$a_n=0$ zu setzen, wenn ein Polynom keinen Term mit $x^n$ besitzt, so gilt
(6) für beliebige nichtnegative ganze Zahlen $n$ (d.h. für alle $n\in\mathbb{N}_0$).
Damit ergibt sich der allgemeine
Satz:
Sei $f$ ein Polynom, und sei $a_n$ der Koeffizient von $x^n$ im Funktionsterm $f(x)$.
Dann gilt
$a_n={\Large f^{(n)}(0)\over \Large n!}$
für alle $n\in\mathbb{N}_0$ (d.h. für $n=0,1,2,3,\dots$).
|
|
$(7)$ |
Damit können wir eine Polynomfunktion gänzlich durch die Werte $f^{(n)}(0)$ ausdrücken.
Haben wir etwa ein Polynom vom Grad $5$ vor uns, also
|
$f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4 +a_5 x^5$
|
, |
|
$(8)$ |
so setzen wir einfach für jeden Koeffizienten den in (7) angegebenen Wert ein und erhalten mit
|
$$f(x)=\underbrace{{f^{(0)}(0)\over 0!}}_{\Large f(0)} +
\underbrace{{f^{(1)}(0)\over 1!}}_{\Large f'(0)}\,x +
{f^{(2)}(0)\over 2!}x^2 +
{f^{(3)}(0)\over 3!}x^3 +
{f^{(4)}(0)\over 4!}x^4 +
{f^{(5)}(0)\over 5!}x^5$$
|
|
|
$(9)$ |
eine Form, in der $f(x)$ alleine durch die Ableitungen $f^{(n)}(0)$ ausgedrückt ist.
Das Ganze könnte man als Kuriosum ohne tiefere Bedeutung abtun, wenn nicht... Und jetzt kommen wir zum eigentlichen Thema
dieses Kapitels!
|
| | |

Faktorielle
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Wichtige Fragen – Potenzreihen und Taylorreihen
Ausgerüstet mit dem Satz (7) und dem Beispiel (9), das sich auf Polynome beliebigen Grades
übertragen lässt, können wir uns fragen, ob es außer Polynomen noch andere Funktionen gibt, für die eine Beziehung
wie (9) gilt. Die Antwort lautet zunächst einmal nein, da ja die rechte Seite von
(9) immer ein Polynom ist. Aber wie wäre es, wenn die Summe nicht abbricht, d.h. wenn wir
unendlich viele derartige Terme addieren könnten? Also:
- Frage 1: Gibt es Funktionen, für die eine Darstellung analog zu (9) gilt, aber mit unendlich vielen Summanden?
Für solche Funktionen müsste also
|
$$f(x)=\underbrace{{f^{(0)}(0)\over 0!}}_{\Large f(0)} +
\underbrace{{f^{(1)}(0)\over 1!}}_{\Large f'(0)}\,x +
{f^{(2)}(0)\over 2!}x^2 +
{f^{(3)}(0)\over 3!}x^3 +
{f^{(4)}(0)\over 4!}x^4 +
{f^{(5)}(0)\over 5!}x^5 + \dots$$
|
|
|
$(10)$ |
gelten, wobei wir uns unter den Punkten am Ende alle (unendlich vielen) weiteren Terme, die nach dem gleichen Muster
gebildet werden, vorstellen.
Jede Funktion, für die diese Beziehung gelten würde, wäre – sofern beliebig hohe Potenzen von $x$ auftreten – kein Polynom.
In gewissem Sinn könnte man sie als "Polynom unendlichen Grades" ansehen. Wenn wir die in (7)
angegebene Formel benutzen, um wie bei Polynomen Koeffizienten $a_n$ zu definieren und anstelle der $f^{(n)}$ einzusetzen, so hätte sie
eine Darstellung der Form
|
$$f(x)=a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + a_5 x^5 + \dots$$
|
. |
|
$(11)$ |
Formal stünden dann (11) und (10) in der gleichen Beziehung zueinander
wie (8) und (9), mit dem Unterschied, dass wir es nun
mit unendlich vielen Koeffizienten $a_n$ zu tun hätten.
- Frage 2: Falls es derartige Funktionen wirklich gibt – sind vielleicht auch Funktionen darunter, die wir bereits kennen?
| | | |
| |
| | |
An dieser Stelle ist es zweckmäßig, sich an den Begriff der Reihe zu erinnern.
Er wurde im Kapitel über Grenzprozesse besprochen und liefert uns genau das, was wir hier brauchen:
eine "unendliche Summe". Formal wird aus einer solchen Ansammlung unendlich vieler Zahlen, die addiert werden sollen,
zunächst eine Folge konstruiert: die erste Zahl, die Summe der ersten zwei Zahlen, die Summe der ersten drei Zahlen usw.
Wenn diese Folge der Partialsummen einen Grenzwert besitzt, so nennen wir ihn den Wert (oder die Summe) der Reihe.
In diesem Sinn können wir – manchmal – tatsächlich unendlich viele Zahlen addieren.
| | | |

Reihe
| |
| | |
Ein Ausdruck wie (11) ist nun für jede reelle Zahl $x$ eine derartige Reihe.
Er sieht zwar aus wie ein "Polynom unendlichen Grades", aber um den dafür üblichen Ausdruck zu verwenden, nennen wir ihn eine
Potenzreihe. Wenn eine Potenzreihe für ein gegebenes $x$ konvergiert, so können wir ihren Wert
mit beliebiger Genauigkeit numerisch berechnen, indem wir zwar nicht alle, aber hinreichend viele der Summanden
addieren! Dass dabei eine wirklich beliebige Genauigkeit erzielt werden kann, ergibt sich einfach aus der genauen Definition
des Grenzwerts, die Sie vielleicht jetzt noch einmal kurz nachlesen wollen: Die Glieder der Folge der Partialsummen, die
jedes für sich eine Näherung der Reihe darstellen, kommen ihrem Grenzwert
(dem Wert der Reihe) beliebig nahe.
Und nun kommt die wirklich gute Nachricht:
Ja, es gibt viele interessante Funktionen $f$, für die die Beziehung (10)
– zumindest für gewisse Zahlen $x$ – gilt!
Ist $f$ eine solche Funktion, so nennen wir die rechte Seite von (10)
ihre Taylorreihe (oder ihre Taylorentwicklung) mit Mittelpunkt $0$.
Die Koeffizienten $a_n$ heißen Taylorkoeffizienten.
|
|
Die Geschichte mit dem "Mittelpunkt" klären wir später. Zuerst wollen Sie sicher wissen, um welche Funktionen
es sich dabei handelt. Die Antwort: die meisten Funktionen, die Sie kennen! Insbesondere – mit wenigen Ausnahmen – fast alle,
die oben zu Beginn des Kapitels aufgezählt wurden, also auch Exponential-, Logarithmus- und Winkelfunktionen.
Desgleichen lassen sich Funktionen, die Brüche und Wurzeln enthalten, in eine Taylorreihe entwickeln, und auch
weitgehend beliebige Kombinationen all dieser. Man muss dabei immer ein bisschen aufpassen,
weil (10) manchmal nicht für alle reellen Zahlen $x$ gilt, und bisweilen hat man es mit Funktionen zu tun, bei
denen die Sache nicht klappt, aber alles in allem eröffnet sich uns hier ein herrliches Stück anwendungsträchtiger
Mathematik.
Im Folgenden stellen wir einige der wichtigsten Taylorreihen vor. Genau genommen müsste man in jedem Fall überprüfen,
ob alle auftretenden Ableitungen existieren, ob die (zunächst formal) angeschriebene Reihe nun tatsächlich konvergiert
und ob (bzw. für welche Werte von $x$) sie mit der gegebenen Funktion übereinstimmt.
Mit einem Wort, man müsste etliche mathematische Beweise führen. Wir werden das aber nur in wenigen Fällen tun
und in allen anderen einfach die Ergebnisse angeben.
| | | |

Grenzwert
*
Partialsummen und
der Wert einer Reihe
| |
| | |
Die Taylorreihe der Exponentialfunktion
Keine andere Taylorreihe ist so einfach zu ermitteln wie die der durch $f(x)= e^x$ definierten Exponentialfunktion zur Basis $e$.
Da die Ableitung von $e^x$ wieder $e^x$ ist, sind alle höheren Ableitungen ebenfalls gleich $e^x$. Es gilt also $f^{(n)}(x)=e^x$
für alle $n\in\mathbb{N}_0$.
Mit $e^0=1$ folgt $f^{(n)}(x)=1$ für alle $n\in\mathbb{N}_0$. Daher ist der $n$-te Taylorkoeffizient durch $a_n={1\over n!}$ gegeben,
womit (11) die Form
|
$\begin{eqnarray}e^x &=& {1\over 0!} + {x\over 1!} + {x^2\over 2!} + {x^3\over 3!} + {x^4\over 4!} + {x^5\over 5!} + \dots\\
&=&1 + x + {x^2\over 2} + {x^3\over 6} + {x^4\over 24} + {x^5\over 120} + \dots\end{eqnarray}$
|
|
|
$(12)$ |
annimmt. Ohne Beweis merken wir an, dass zwei Aussagen gelten:
- Die rechte Seite von (12) ist für jedes reelle $x$ eine konvergente Reihe.
- Ihr Wert stimmt für jedes reelle $x$ mit $e^x$ überein.
| | | |

e als natürliche
Basis

Ableitung der
Exponentialfunktion
| |
| | |
Für $x=1$ ergibt sich mit
|
$\begin{eqnarray}e &=& {1\over 0!} + {1\over 1!} + {1\over 2!} + {1\over 3!} + {1\over 4!} + {1\over 5!} + \dots\\
&=&1 + 1 + {1\over 2} + {1\over 6} + {1\over 24} + {1\over 120} + \dots\end{eqnarray}$
|
|
|
$(13)$ |
eine Reihe für die Zahl $e$, der wir bereits im Kapitel über Grenzprozesse begegnet sind.
Wir führen anhand der Taylorreihe (12) vor, wie die Exponentialfunktion durch Polynome
approximiert (d.h. angenähert) werden kann. Dazu bilden wir für jedes $k\in\mathbb{N}_0$ die Partialsumme,
die sich ergibt, indem wir nur bis zum Reihenglied vom Grad $k$ (also jenem mit $x^k$) aufsummieren.
- $p_0(x) = 1$ ist jene konstante Funktion, die mit $e^x$ an der Stelle $x=0$ übereinstimmt.
- $p_1(x) = 1+x$ ist jenes Polynom ersten Grades, das an der Stelle $x=0$ den gleichen Funktionwert und die gleiche erste Ableitung wie $e^x$ besitzt.
- $p_2(x) = 1+x+{\Large {x^2\over 2}}$ ist jenes Polynom zweiten Grades, das an der Stelle $x=0$ den gleichen Funktionwert, die gleiche erste und die gleiche zweite Ableitung wie $e^x$ besitzt.
- $p_3(x) = 1+x+{\Large {x^2\over 2}}+{\Large {x^3\over 6}}$ ist jenes Polynom dritten Grades, das an der Stelle $x=0$ den gleichen Funktionwert und die gleichen Ableitungen bis zur dritten Ordnung wie $e^x$ besitzt.
- Allgemein ist $p_k(x)=1+x+\dots+{\Large {x^k\over k!}}$ jenes Polynom $k$-ten Grades, das an der Stelle $x=0$ den gleichen Funktionwert und die gleichen Ableitungen bis zur $k$-ten
Ordnung wie $e^x$ besitzt.
Wir nennen $p_k$ das $k$-te Taylorpolynom (oder Näherungspolynom) der Exponentialfunktion.
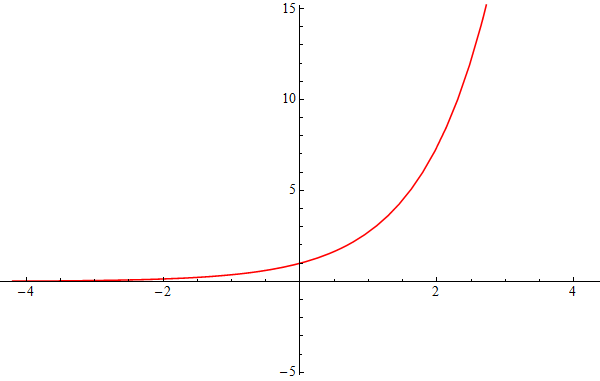
Die folgende dynamische Abbildung zeigt den Graphen der Exponentialfunktion (rot) zusammen mit jeweils einem
Taylorpolynom (blau), wenn Sie die Maus über die Bezeichnungen $p_0(x)$ bis $p_9(x)$ führen:
| Die Exponentialfunktion und ihre Taylorpolynome |
 |
| $p_0(x)$ |
$p_1(x)$ |
$p_2(x)$ |
$p_3(x)$ |
$p_4(x)$ |
$p_5(x)$ |
$p_6(x)$ |
$p_7(x)$ |
$p_8(x)$ |
$p_9(x)$ |
Es ist deutlich sichtbar, dass sich der Graph des Taylorpolynoms $p_k$ umso besser an jenen der Exponentialfunktion
schmiegt, je größer $k$ ist. Keines der Taylorpolynome stellt die Exponentialfunktion exakt dar, aber
für jedes festgehaltene $x$ wird die Abweichung für genügend große $k$ beliebig klein. Das lässt sich
auch durch die entsprechenden Zahlenwerte illustrieren: So ist beispielsweise $e^2 = 7.3890...$, was durch $p_9(2) = 7.3887...$
mit einer Abweichung von weit unter einem Promille schon sehr gut approximiert wird.
| | | |

Reihe für e
| |
| | |
Die Taylorreihen von Sinus und Cosinus
Die Taylorreihen der Sinus- und der Cosinusfunktion werden ebenfalls durch die Berechnung der höheren Ableitungen ermittelt.
Dabei müssen wir nur die Ableitungsregeln $(\sin x)'=\cos x$ und $(\cos x)'=-\sin x$ sowie die Beziehungen $\sin(0)=0$ und $\cos(0)=1$
verwenden. Es folgt, dass jeder zweite Taylorkoeffizient gleich $0$ ist, und dass die verbleibenden Taylorkoeffizienten
abwechselnde Vorzeichen besitzen. Um im Detail anzusehen, wie sie berechnet werden,
klicken Sie auf den nebenstehenden Button!
Die Ergebnisse sind
|
$\begin{eqnarray}\sin x &=& {x\over 1!} - {x^3\over 3!} + {x^5\over 5!} - {x^7\over 7!} + {x^9\over 9!} - {x^{11}\over 11!} + \dots\\
&=&x - {x^3\over 6} + {x^5\over 120} - {x^7\over 5040} + \dots\end{eqnarray}$
|
|
|
$(14)$ |
und
|
$\begin{eqnarray}\cos x &=& {1\over 0!} - {x^2\over 2!} + {x^4\over 4!} - {x^6\over 6!} + {x^8\over 8!} - {x^{10}\over 10!} + \dots\\
&=&1 - {x^2\over 2} + {x^4\over 24} - {x^6\over 720} + \dots\end{eqnarray}$
|
|
|
$(15)$ |
Auch diese beiden Reihen konvergieren für jedes reelle $x$ und erlauben uns, die Sinus- und die Cosinusfunktion beliebig gut zu
approximieren.
Auch hier können wir wieder die Taylorpolynome betrachten. Sehen wir uns die ersten Taylorpolynome der Sinusfunktion an:
Da generell $p_k$ das Polynom ist, das eine Taylorreihe bis zum Glied vom Grad $k$ aufsummiert, und da für die Sinusfunktion
alle Taylorkoeffizienten $a_k$ mit geradem $k$ gleich $0$ sind, ist $p_0 = 0$, und danach.sind immer zwei aufeinander folgende
Taylorpolynome gleich: $p_1 = p_2$, $p_3 = p_4$, $p_5 = p_6$ usw.
Die folgende dynamische Abbildung zeigt den Graphen der Sinusfunktion (rot) zusammen mit jeweils einem
Taylorpolynom (blau), wenn Sie die Maus über die Bezeichnungen $p_1(x)$ bis $p_{19}(x)$ führen:
| Die Sinusfunktion und ihre Taylorpolynome |
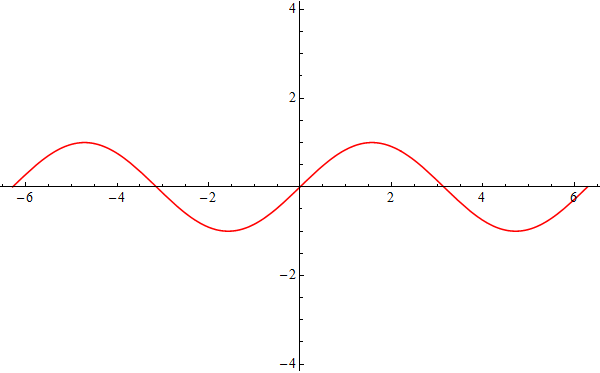 |
| $p_1(x)$ |
$p_3(x)$ |
$p_5(x)$ |
$p_7(x)$ |
$p_9(x)$ |
$p_{11}(x)$ |
$p_{13}(x)$ |
$p_{15}(x)$ |
$p_{17}(x)$ |
$p_{19}(x)$ |
Ab $p_{17}$ ist in dieser grafischen Darstellung – im gezeigten Intervall – kein Unterschied mehr zur Sinusfunktion erkennbar.
Auch in diesem Fall belegen die Zahlenwerte die Güte der Approximation auf beeindruckende Weise: So wird $\sin(4)=-0.75680249...$ durch
$p_{19}(4)=-0.75680257...$ mit einer relativen Abweichung von nur $10^{-7}$ approximiert. Je größer $|x|$ ist, umso
mehr weichen die Taylorpolynome von der Sinusfunktion ab, wie etwa der Plot der Sinusfunktion gemeinsam mit $p_{19}$ in einem
vergrößerten Intervall zeigt:
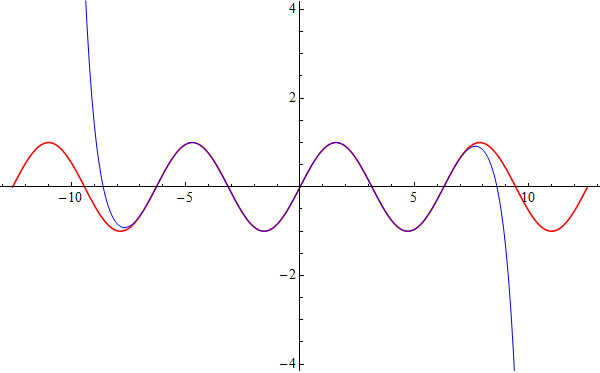
Aber immerhin ist für jedes $x$, und sei sein Betrag noch so groß, ab einem Taylorpolynom mit genügend großem $k$
die Abweichung beliebig klein!
| | | |

Ableitungen der
Winkelfunktionen
| |
| | |
Die geometrische Reihe
Die Taylorreihen (12), (14) und (15) haben wir durch Berechnung
aller höheren Ableitungen an der Stelle $0$ ermittelt. Das ist die direkte Methode, die von der in
(7) angeschriebenen Beziehung $a_n = f^{(n)}/n!$ Gebrauch macht, um die Taylorkoeffizienten zu erhalten.
Das funktioniert zwar bei allen Funktionen, die sich in eine Taylorreihe entwickeln lassen, ist aber manchmal mühsamer
als bei den obigen Beispielen. Taylorreihen können aber auch auf andere Weise erhalten werden. Das berühmteste und
wichtigste Beispiel dieser Art haben wir bereits im Kapitel über Grenzprozesse kennen gelernt: die
geometrische Reihe. Ganz ohne Benutzung der Ableitung haben wir dort das Ergebnis erhalten, dass
für alle reellen $x$, die $|x|<1$ erfüllen,
|
$$1 + x + x^2 + x^3 + x^4 + x^5 +\dots = {1\over 1-x}$$
|
|
|
$(16)$ |
gilt. (Im Kapitel über Grenzprozesse haben wir $q$ anstelle von $x$ geschrieben, und dann war da noch ein
erstes Reihenglied $a_0$, das hier $1$ gesetzt ist). Lesen wir diese Beziehung nun verkehrt herum, also in der Form
|
$${1\over 1-x} = 1 + x + x^2 + x^3 + x^4 + x^5 +\dots$$
|
, |
|
$(17)$ |
| | | |

geometrische Reihe
| |
| | |
so haben wir hier nichts anderes vor uns als die Taylorreihe der Funktion $x\mapsto {1\over 1-x}$. Sie konvergiert nur,
wenn $|x|<1$ ist, besitzt also als Konvergenzbereich das offene Intervall $(-1,1)$, im Unterschied zu den Taylorreihen
(12), (14) und (15), deren Konvergenzbereich
ganz $\mathbb{R}$ ist.
Anmerkung: Vielleicht ist Ihnen aufgefallen, dass in diesem Argument eine Kleinigkeit fehlt: Es kann zwar ${1\over 1-x}$ im Intervall $(-1,1)$ durch
die geometrische Reihe (17) dargestellt werden, aber was garantiert uns, dass das auch tatsächlich die Taylorreihe
der Funktion $x\mapsto {1\over 1-x}$ ist? Wir haben hier die Tatsache benutzt, dass die Taylorreihe eindeutig ist:
Kann eine Funktion als Potenzreihe dargestellt werden, so ist das automatisch ihre Taylorreihe! Wenn Sie das beweisen wollen,
so bilden Sie Schritt für Schritt die höheren Ableitungen von
$f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3+\dots$,
setzen danach $x=0$ ein und erhalten $f(0)=a_0$, $f'(0)=a_1$, $f''(0)=2a_2$, $f^{(3)}(0)=a_3\cdot 3!$ usw., genau so, wie wir es
oben für
Polynome gemacht haben. Allgemein ergibt sich die Beziehung $f^{(n)}(0)=a_n\cdot n!$, die eine Taylorreihe charakterisiert.
Auch im Fall der geometrischen Reihe ist es instruktiv, sich die ersten Taylorpolynome anzusehen:
| Die Funktion $x\mapsto {1\over 1-x}$ und ihre Taylorpolynome |
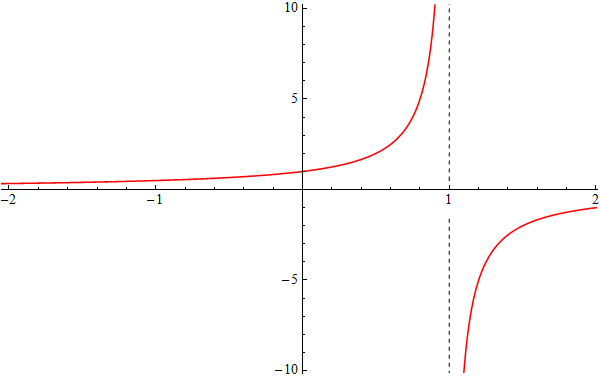 |
| $p_0(x)$ |
$p_1(x)$ |
$p_2(x)$ |
$p_3(x)$ |
$p_4(x)$ |
$p_5(x)$ |
$p_6(x)$ |
$p_7(x)$ |
$p_8(x)$ |
$p_9(x)$ |
Dass kein Taylorpolynom $p_k$ es schafft, dem immer steiler ("ins Unendliche") ansteigenden roten
Graphen nahe $x=1$ zu folgen und danach den Sprung hinunter ("nach minus Unendlich") mitzumachen, ist intuitiv einsichtig,
und daher auch, dass die geometrische Reihe jenseits von $x=1$ nicht mehr konvergiert. Interessant ist aber, dass die Konvergenz
jenseits der gespiegelten Stelle $x=-1$ ebenfalls nicht mehr gegeben ist. Aber immerhin kann die Funktion
$x\mapsto {1\over 1-x}$ für jedes festgehaltene $x$ innerhalb des Bereichs $-1 < x < 1$ durch Taylorpolynome
$p_k$ mit genügend großem $k$ beliebig genau approximiert werden.
| | | |

Intervalle
| |
| | |
Weitere Taylorreihen
In der folgenden Tabelle sind einige Taylorreihen (zusammen mit den obigen) und den jeweiligen
Konvergenzbereichen zusammengestellt. Wir gehen auf ihre Herleitungen nicht näher ein. Im Prinzip können sie alle
durch Berechnung aller höheren Ableitungen an der Stelle $x=0$ gefunden werden.
| Funktion |
Taylorreihe mit Mittelpunkt $0$ |
Konvergenzbereich |
Anmerkung |
| $e^x$ |
$\begin{eqnarray}&&{1\over 0!} + {x\over 1!} + {x^2\over 2!} + {x^3\over 3!} + {x^4\over 4!} + {x^5\over 5!} + \dots\\
&=&1 + x + {x^2\over 2} + {x^3\over 6} + {x^4\over 24} + {x^5\over 120} + \dots\end{eqnarray}$
|
$\mathbb{R}$ |
|
| $\sin x$ |
$\begin{eqnarray}&& {x\over 1!} - {x^3\over 3!} + {x^5\over 5!} - {x^7\over 7!} + {x^9\over 9!} - {x^{11}\over 11!} + \dots\\
&=&x - {x^3\over 6} + {x^5\over 120} - {x^7\over 5040} + \dots\end{eqnarray}$
|
$\mathbb{R}$ |
|
| $\cos x$ |
$\begin{eqnarray}&& {1\over 0!} - {x^2\over 2!} + {x^4\over 4!} - {x^6\over 6!} + {x^8\over 8!} - {x^{10}\over 10!} + \dots\\
&=&1 - {x^2\over 2} + {x^4\over 24} - {x^6\over 720} + \dots\end{eqnarray}$
|
$\mathbb{R}$ |
|
| $$1\over 1-x$$ |
$$1 + x + x^2 + x^3 + x^4 + x^5 + x^6 + \dots$$
(geometrische Reihe)
|
$(-1,1)$ |
Spezialfall der
binomischen Reihe
(s.u.) für $\alpha=-1$
und $x\to -x$ |
| $$(1+x)^\alpha$$ mit $\alpha\in\mathbb{R}$ |
$\begin{eqnarray}&& \left(\begin{array}{c}\alpha\\0\end{array}\right) + \left(\begin{array}{c}\alpha\\1\end{array}\right)x + \left(\begin{array}{c}\alpha\\2\end{array}\right)x^2
+\left(\begin{array}{c}\alpha\\3\end{array}\right)x^3 + \dots\\
&=&1 + \alpha\,x + {\alpha(\alpha-1)\over 2!}x^2 + {\alpha(\alpha-1)(\alpha-2)\over 3!}x^3 + \dots\end{eqnarray}$
(binomische Reihe)
|
$(-1,1)$, wenn $\alpha < 0$
$[-1,1]$, wenn $0 < \alpha\notin\mathbb{N}_0$
$\mathbb{R}$, wenn $\alpha\in\mathbb{N}_0$ |
zu den hier
auftretenden
Binomialkoeffizienten
siehe den Text unten |
| $$\sqrt{\,1+x}$$ |
$$1 + {x\over 2} - {x^2\over 8} + {x^3\over 16} - {5x^4\over 128} + \dots$$
|
$[-1,1]$ |
Spezialfall der
binomischen Reihe
für $\alpha={1\over 2}$ |
| $$1\over\sqrt{\,1+x}$$ |
$$1 - {x\over 2} + {3x^2\over 8} - {5x^3\over 16} + {35x^4\over 128} - \dots$$
|
$(-1,1)$ |
Spezialfall der
binomischen Reihe
für $\alpha=-{1\over 2}$ |
| $$\ln(1+x)$$ |
$$x - {x^2\over 2} + {x^3\over 3} - {x^4\over 4} + {x^5\over 5} - {x^6\over 6} + \dots$$
|
$(-1,1]$ |
|
| $${\rm atan}\,x$$ |
$$x - {x^3\over 3} + {x^5\over 5} - {x^7\over 7} + {x^9\over 9} - {x^{11}\over 11} + \dots$$
|
$[-1,1]$ |
|
In der binomischen Reihe treten die Binomialkoeffizienten auf. Für reelles $\alpha$ und
$n\in\mathbb{N}$ sind sie definiert durch
|
$$\left(\begin{array}{c}\alpha\\n\end{array}\right) = {\alpha(\alpha-1)(\alpha-2)\dots(\alpha-n+1)\over
n (n-1) (n-2)\,\dots\quad\cdot\,\,\,\,\,\,\,\,\,1\,\,\,\,\,\qquad}$$
|
|
|
$(18a)$ |
(wobei im Zähler und im Nenner gleich viele Faktoren stehen), beispielsweise
|
$$\left(\begin{array}{c}1/2\\3\end{array}\right) = {{1\over 2}({1\over 2}-1)({1\over 2}-2)\over
3\,\,\,\cdot\,\,\, 2\quad\cdot\quad\,\,\,1\quad\,\,\,\,\,} = {1\over 16}$$
|
. |
|
|
Für den Spezialfall $n=0$ wird
|
$$\left(\begin{array}{c}\alpha\\0\end{array}\right) = 1$$
|
|
|
$(18b)$ |
| | | |
| |
| | |
gesetzt. Für $\alpha\in\mathbb{N}_0$ sind die Binomialkoeffizienten bereits früher aufgetreten – hier werden
sie für beliebiges reelles $\alpha$ verallgemeinert. So können beispielsweise mit Hilfe von (18a)
und den Spezialfällen $\alpha={1\over 2}$ und $\alpha=-{1\over 2}$ die Taylorreihen für
$\sqrt{\,1+x}$ und $1\over\sqrt{\,1+x}$ bis zu beliebig hoher Ordnung angeschrieben werden. (In der obigen Tabelle sind
sie bis zur vierten Ordnung angegeben).
Um Taylorreihen kompakt anzuschreiben, wird oft das Summensymbol verwendet, genauso, wie es
bereits im Kapitel über Grenzprozesse gemacht wurde. Damit lauten etwa die Taylorreihen für die
Exponentialfunktion, die geometrische Reihe und die binomische Reihe
|
$$e^x = \sum_{n=0}^\infty\,{x^n\over n!}$$
|
,
|
$${1\over 1-x} = \sum_{n=0}^\infty\,x^n$$
|
und
|
$$(1+x)^\alpha = \sum_{n=0}^\infty\,\left(\begin{array}{c}\alpha\\n\end{array}\right)x^n$$
|
. |
|
$(19)$ |
Um die Sinus- und die Cosinusfunktion ebenso kompakt anzuschreiben, benutzt man die Tatsache, dass die ungeraden
Zahlen in der Form $2k+1$ (mit $k=0,1,2,\dots$) und die geraden Zahlen in der Form $2k$ (mit $k=0,1,2,\dots$)
durchnummeriert werden können. Die wechselnden Vorzeichen bekommen wir in den Griff, indem wir bedenken, dass
$(-1)^k$ gleich $1$ oder $-1$ ist, je nachdem, ob $k$ gerade oder ungerade ist. Damit ergibt sich
|
$$\sin x = \sum_{k=0}^\infty\,(-1)^k {x^{2k+1}\over (2k+1)!}$$
|
und
|
$$\cos x = \sum_{k=0}^\infty\,(-1)^k {x^{2k}\over (2k)!}$$
|
. |
|
$(20)$ |
Um ein Beispiel einer Anwendung der obigen Taylorreihen anzugeben, betrachten wir jene für die Arcustangensfunktion,
die in der obigen Tabelle angegeben wurde.
Da $\tan({\pi\over 4})=1$ und daher ${\rm atan}\,(1)={\pi\over 4}$ gilt, und da $1$ im Konvergenzbereich der Taylorreihe
des Arcustangens liegt, folgt durch Einsetzen von $x=1$
|
$${\pi\over 4}= 1 - {1\over 3} + {1\over 5} - {1\over 7} + {1\over 9} - {1\over 11} + \dots$$
|
. |
|
$(21)$ |
Damit ist eine Methode gefunden, die Zahl $\pi$ durch eine Reihe beliebig genau zu approximieren!
Sie konvergiert nicht aufregend gut (die Summe der ersten 32 Glieder liefert $\pi$ auf ein Prozent genau, und für
eine Genauigkeit von unter 1 Promille werden die ersten 319 Glieder benötigt), aber immerhin ist mit Ergebnissen wie
diesen oder der Reihe (13) für $e$ grundsätzlich der Weg gewiesen,
irrationale Zahlen durch Reihen auszudrücken und auf diese Weise numerisch beliebig genau zu berechnen.
Ein weiteres Beispiel ergibt sich, indem die Reihe für
$\sqrt{\,1+x}$ an der Stelle $x=1$ ausgewertet wird, um $\sqrt{2}$ zu approximieren, und mit $x=1$ in der
Reihe für $x\mapsto\ln(1+x)$ kann $\ln 2$ numerisch berechnet werden.
Darüber hinaus kann mit Taylorreihen in vielerlei Hinsicht gerechnet werden: Wenn Sie beispielsweise die Reihe (12) für $e^x$ gliedweise – also
Term für Term – differenzieren, so erhalten sie wieder $e^x$, und auf die gleiche Art können Sie die
Ableitungsregeln $(\sin x)'=\cos x$ und $(\cos x)'=-\sin x$ aus den Reihen (14) und (15) erhalten.
Das Gleiche gilt für Stammfunktionen und bestimmte Integrale (sofern die Integrationsgrenzen innerhalb des Konvergenzbereichs
liegen).
| | | |

Binomialkoeffizienten

Summensymbol
| |
| | |
Die häufigste Methode: Bekannte Taylorreihen nutzen
Taylorreihen von Funktionen, die sich auf die in der obigen Tabelle angegebenen zurückführen lassen,
ergeben sich oft sehr einfach aus den entsprechenden Reihen für diese.
Beispielsweise kann die Taylorreihe der Funktion $f(x)=\sin(2x)$ gefunden werden,
indem wir in der Taylorreihe für $\sin x$ einfach $x$ durch $2x$ ersetzen. Der Grund dafür ist sehr einfach:
Für jedes reelle $x$ ist auch $2x$ eine reelle Zahl! So erhalten wir
|
$\begin{eqnarray}\sin (2x) &=& {2x\over 1!} - {(2x)^3\over 3!} + {(2x)^5\over 5!} - {(2x)^7\over 7!} + {(2x)^9\over 9!} - {(2x)^{11}\over 11!} + \dots\\
&=&2x - {(2x)^3\over 6} + {(2x)^5\over 120} - {(2x)^7\over 5040} + \dots\\
&=&2x - {8x^3\over 6} + {32x^5\over 120} - {128x^7\over 5040} + \dots\\
&=&2x - {4x^3\over 3} + {4x^5\over 15} - {3x^7\over 315} + \dots\end{eqnarray}$
|
|
|
$(22)$ |
Weitere Beispiele, neue Taylorreihen ohne großen Aufwand aus bekannten zu gewinnen,
liefert die geometrische Reihe (17): Wird in ihr $x$ durch $-x$ ersetzt, so ergibt sich
|
$${1\over 1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 +\dots = \sum_{n=0}^\infty\,(-1)^n x^n$$
|
. |
|
$(23)$ |
Der Konvergenzbereich dieser Reihe ist ebenfalls das offene Intervall $(-1,1)$. Ganz analog können Sie auch die
Taylorreihen von Funktionen wie $x\mapsto {1\over 1 + x^2}$ oder $x\mapsto \sqrt{1 - x^2}$ oder $x\mapsto \cos({x\over 2})$ ermitteln.
Ein besonders schönes Beispiel ergibt sich, indem beide Seiten der Beziehung (14) durch $x$ dividiert
werden: Mit
|
$\begin{eqnarray}{\sin x\over x} &=& {1\over 1!} - {x^2\over 3!} + {x^4\over 5!} - {x^6\over 7!} + {x^8\over 9!} - {x^{10}\over 11!} + \dots\\
&=&1 - {x^2\over 6} + {x^4\over 120} - {x^6\over 5040} + \dots\end{eqnarray}$
|
|
|
$(24)$ |
| | | |
| |
| | |
ist gezeigt, dass der Quotient ${\sin x\over x}$, der für $x=0$ nicht definiert ist, für kleine $x$ ungefähr gleich
$1$ ist. Die Näherung "$\sin x\approx x$ für kleine $x$" haben wir bereits im Kapitel über die Winkelfunktionen
gefunden (damals in der Form "$\sin \alpha\approx \alpha$ für kleine $\alpha$" angeschrieben).
Nehmen wir noch den nächsten Term dazu, betrachten also das Taylorpolynom zweiten Grades,
so ergibt sich mit ${\sin x\over x}\approx p_2(x)=1-{x^2\over 6}$, dass sich der Graph von ${\sin x\over x}$ in der Nähe der
Stelle $x=0$ an den Graphen von $1-{x^2\over 6}$ (d.h. an eine nach unten offene Parabel) anschmiegt.
Die folgende Abbildung zeigt den Graphen von
${\sin x\over x}$ (rot) zusammen mit jenem von $p_2$ (blau):
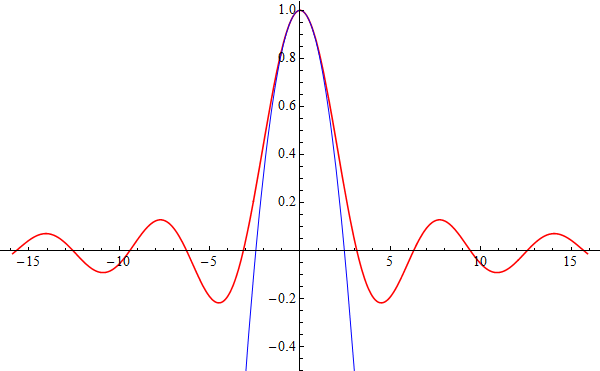
Dieses Beispiel unterstreicht noch einmal, wie Taylorreihen über das Verhalten einer Funktion in der Nähe der Stelle $x=0$
Auskunft geben.
| | | |

kleine Winkel
| |
| | |
Wann es nicht klappt
Aus dem Bisherigen könnte der Eindruck entstehen, dass alle Funktionen in eine Taylorreihe entwickelt werden können.
Das ist allerdings nicht der Fall. Zunächst ist für die Existenz eier Taylorreihe (mit Mittelpunkt $0$)
nötig, dass alle Ableitungen an der Stelle $0$ bis zu beliebigen Ordnungen existieren,
d.h. dass die Funktion an der Stelle $0$ beliebig oft ("unendlich oft") differenzierbar ist. Dafür reicht es nicht aus,
dass sich formal Terme für die Ableitungen hinschreiben lassen – sie müssen auch an der Stelle $0$
wohldefiniert sein, d.h. endliche Werte besitzen. Damit scheiden bereits einige Funktionen von vornherein aus, beispielsweise diese:
- $f(x)=|x|$ ist an der Stelle $0$ nicht differenzierbar. (Der Graph besitzt dort einen Knick).
- $f(x)=\sqrt{x}$ lässt sich zwar formal differenzieren ($f'(x)={1\over 2\sqrt{x}}$), aber die Ableitung an der Stelle $0$
ist nicht endlich.
- Die Funktion $f(x)={1\over x}$ scheidet aus, weil sie bei $x=0$ nicht definiert ist.
Aber nicht einmal alle beliebig oft differenzierbaren Funktionen lassen sich in eine Taylorreihe entwickeln.
Klicken Sie auf den nebenstehenden Button für ein Beispiel!
Funktionen, die sich in eine Taylorreihe entwickeln lassen, heißen analytisch, und
nicht jede beliebig oft differenzierbare Funktion ist analytisch.
Sie können sich aber an die folgende Faustregel halten: Eine Funktion $f$,
- die sich unter Verwendung der Grundrechnungsarten
aus beliebigen Polynomen, Potenzfunktionen (einschließlich Wurzeln), Exponential- und Logarithmusfunktionen
sowie Winkelfunktionen aufbauen lässt,
- für die $f(0)$ wohldefiniert ist,
- und für die bei der Berechnung von $f(0)$ keine Potenz von $0$ (also auch keine Wurzel $\sqrt{0}$)
und kein Logarithmus von $0$ auftritt,
lässt sich in eine Taylorreihe mit Mittelpunkt $0$ entwickeln.
Das ist beispielsweise für $f(x)=e^{-x}\sqrt{2-x}$ der Fall, da bei der Berechnung
$f(0)=e^{-0}\sqrt{2-0}=\sqrt{2}$ weder eine Wurzel noch ein Logarithmus von $0$ auftritt.
Hingegen ist diese Bedingung für die Funktion $f(x)=\sqrt{\sin x}$ nicht erfüllt, wie die
Berechung $f(0)=\sqrt{\sin 0}=\sqrt{0}$ zeigt.
| | | |

Betragsfunktion
| |
| | |
Rechnen mit Näherungsordnungen
Wie wir bereits gesehen haben, dienen die Taylorpolynome dazu, Funktionen zu approximieren.
So wird beispielsweise die Sinusfunktion für kleine $x$ durch ihr Taylorpolynom dritter Ordnung
$p_3(x)=x-{x^3\over 6}$ angenähert. Um auszudrücken, ab welcher Ordnung Terme der Taylorreihe weggelassen wurden,
ist die Schreibweise
|
$$\sin x = x -{x^3\over 6} + O(x^5)$$
|
|
|
$(25)$ |
üblich. Das Symbol $O(x^5)$ sprechen wir aus als "Ordnung $x^5$". Es steht für eine Potenzreihe, die mit
einem $x^5$-Term beginnt, also allgemein von der Form $a_5x^5 + a_6 x^6 +\dots$ ist. Stellen wir uns auf den Standpunkt,
von der Sinusfunktion nur (25), also den Beginn der Taylorreihe zu kennen, so lassen sich damit
zumindest Aussagen über ihren Wert und ihre Ableitungen bis zur vierten Ordnung an der Stelle $0$ treffen.
Sind die Beträge der (als unbekannt angenommenen) Koeffizienten $a_5,a_6,\dots$ nicht allzu groß, so
stellt (25) auch für Werte $x\neq 0$, solange ihr Betrag klein ist, eine Näherungsformel
für $\sin x$ in der Nähe der Stelle $0$ dar. Mit dem Symbol $O(x^5)$ in (25) wird angegeben, bis zu welcher
Ordnung in $x$ die Näherung $\sin x \approx x -{x^3\over 6}$ zu verstehen ist.
Mit Ausdrücken dieser Form lässt sich auch rechnen. Schreiben wir etwa auch den Beginn der Taylorreihe der
Exponentialfunktion in der Form $e^x=1+x+{x^2\over 2}+O(x^3)$ an, so können wir die ersten Glieder der Taylorreihe
des Produkts $e^x \sin x$ bequem in der Form
|
$\begin{eqnarray}e^x \sin x &=& \left(1 + x + {x^2\over 2} + O(x^3)\right)\left(x -{x^3\over 6} + O(x^5)\right)\\
&=& x + x^2 + {x^3\over 3} + O(x^4)\end{eqnarray}$
|
|
|
$(26)$ |
ermitteln. Vollziehen Sie diese Rechnung nach!
Dazu multiplizieren Sie einfach die Klammern aus, bedenken, dass $x O(x^3)$ das Gleiche ausdrückt wie $O(x^4)$,
$O(x^3) O(x^5)$ das Gleiche wie $O(x^8)$ usw. und lassen schließlich alle $O$-Symbole weg,
die den bereits auftretenden keine neue Information hinzufügen, ersetzen also etwa $O(x^4) + O(x^5)$ durch
$O(x^4)$. Was übrig bleibt, ist genau das Ergebnis von (26)!
| | | |
| |
| | |
Taylorreihen mit anderem Mittelpunkt
Wir haben bis jetzt Taylorreihen "mit Mittelpunkt $0$" besprochen. Die Taylorkoeffizienten waren gemäß
(7) bzw. (10) und (11) durch alle Ableitungen an der Stelle $0$,
d.h. durch $f^{(n)}(0)$ ausgedrückt. Die Reihenglieder waren dann von der Form $a_n x^n$. Das hat es uns
unter anderem ermöglicht, Funktionen in der Nähe der Stelle $0$ zu approximieren
und damit etwas über ihr Verhalten in der Nähe dieser Stelle zu erfahren.
Manchmal sind aber die Eigenschaften einer Funktion an einer anderen Stelle von Interesse, sagen wir
an der Stelle $x_0$. Allgemein sind die Glieder einer Taylorreihe mit Mittelpunkt $x_0$ von der Form
$a_n (x-x_0)^n$. Alles andere funktioniert genauso wie zuvor! Eine solche Taylorreihe ist also von der Form
|
$\begin{eqnarray}f(x)&=&\underbrace{{f^{(0)}(x_0)\over 0!}}_{\Large f(x_0)} +
\underbrace{{f^{(1)}(x_0)\over 1!}}_{\Large f'(x_0)}\,(x-x_0) +
{f^{(2)}(x_0)\over 2!}(x-x_0)^2 +
{f^{(3)}(x_0)\over 3!}(x-x_0)^3 + \dots\\
&=&a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + a_3 (x-x_0)^3 + a_4 (x-x_0)^4 + \dots\end{eqnarray}$
|
|
|
$(27)$ |
Die Taylorkoeffizienten sind nun durch
|
$$a_n = {f^{(n)}(x_0)\over n!}$$
|
|
|
$(28)$ |
gegeben. Als Beispiel führen wir den Beginn der Taylorreihe mit Mittelpunkt $1$ der Wurzelfunktion
|
$$\sqrt{x} = 1 + {x-1\over 2} - {(x-1)^2\over 8} + {(x-1)^3\over 16} - {5(x-1)^4\over 128} + \dots$$
|
|
|
$(28)$ |
an. Ihr Konvergenzbereich ist das Intervall $[0,2]$.
| | | |
| |
| | |
Restglied
Wenn wir eine Funktion $f$ durch eines ihrer Taylorpolynome $p_k$ approximieren, wollen wir manchmal wissen,
wie groß der dadurch gemachte Fehler maximal ist. Die Differenz $f(x)-p_k(x)$ wird Restglied genannt.
Um es abzuschätzen, gibt es eine Reihe von Kriterien, von denen wir nur eines erwähnen:
Man kann zeigen, dass es zwischen $x$ und dem Mittelpunkt $x_0$ der Reihe eine Stelle $\xi$ gibt, so dass
das Restglied gleich
|
$${f^{(k+1)}(\xi)\over (k+1)!}\,(x-x_0)^{k+1}$$
|
|
|
$(28)$ |
ist. Gelingt es, den Betrag der Ableitungsfunktion $f^{(k+1)}$ im Intervall zwischen $x$ und $x_0$
nach oben abzuschätzen, so kann damit der maximale Fehler der Approximation von $f$ durch $p_k$
angegeben werden.
|
| | |
| |
| | |
| Potenzreihen und ihre Konvergenz |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Potenzreihen allgemein
Die Potenzreihen, die wir bisher kennen gelernt haben, waren Taylorreihen bekannter (und interessanter) Funktionen.
Ganz allgemein ist eine Potenzreihe mit Mittelpunkt $x_0$ eine Reihe der Form
|
$$a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + a_3 (x-x_0)^3 + a_4 (x-x_0)^4 + \dots$$
|
|
|
$(31)$ |
oder, in Summenschreibweise,
|
$$\sum_{n=0}^\infty a_n (x-x_0)^n$$
|
. |
|
$(32)$ |
Dabei können der Mittelpunkt $x_0$ und die Koeffizienten $a_n$ zunächst beliebig vorgegeben werden.
Das erlaubt es, die bisherige Sichtweise umzukehren, $x_0$ und die Koeffizienten $a_n$ frei zu wählen und
durch
|
$$f(x) = \sum_{n=0}^\infty a_n (x-x_0)^n$$
|
|
|
$(33)$ |
eine Funktion zu definieren! Dabei erhebt sich die Frage, für welche $x$ eine solche Reihe konvergieren wird.
Interessanterweise liegt der Konvergenzbereich jeder Potenzreihe symmetrisch zum Mittelpunkt $x_0$.
Es sind drei Fälle möglich:
- Die Reihe konvergiert nur für $x=x_0$. Der Konvergenzbereich besteht in diesem Fall aus einem einzigen Punkt, dem
Mittelpunkt der Reihe, und dort gilt $f(x_0) = a_0$. Das ist der am wenigsten interessante Fall.
- Die Reihe konvergiert in einem Intervall der Form $(x_0-\rho,x_0+\rho)$, nicht aber außerhalb des Intervalls
$[x_0-\rho,x_0+\rho]$, wobei $\rho$, der so genannte Konvergenzradius,
eine positive reelle Zahl ist. An den Randpunkten $x_0-\rho$ und $x_0+\rho$ des Konvergenzbereichs kann die Konvergenz
der Reihe gegeben sein, muss aber nicht. In diesem Fall ist der Konvergenzbereich ein Intervall,
dessen Randpunkte symmetrisch zum Mittelpunkt liegen.
Für die Ermittlung des Konvergenzradius werden wir sogleich zwei Methoden angeben.
- Die Reihe konvergiert für alle reellen Zahlen $x$, d.h. der Konvergenzbereich ist ganz $\mathbb{R}$.
In diesem Fall schreibt man formal $\rho=\infty$.
In den letzten beiden Fällen ist mit (33) eine Funktion definiert, die zumindest in einem Intervall
wohldefiniert ist, das mehr als einen Punkt enthält, und deren Taylorreihe die vorgegebene Potenzreihe ist.
Tatsächlich werden schwierige Probleme der Mathematik (wie beispielsweise das Lösen von Differentialgleichungen,
die in der Physik auftreten) oft durch die Ermittlung der Koeffizienten einer Potenzreihe gelöst, die ihrerseits die
gesuchte Funktion definiert.
| | | |

Differentialgleichungen
(in Vorbereitung)
| |
| | |
Konvergenzradius
Um den Konvergenzradius einer Potenzreihe mit Koeffizienten $a_n$ zu berechnen, gibt es eine Reihe von Methoden, von denen
wir (ohne Beweis) zwei angeben:
Methode 1: Sind ab einem bestimmten Index alle $a_n\neq 0$, und existiert der Grenzwert
|
$$\lim_{n\to\infty}\left|{a_n\over a_{n+1}}\right|$$
|
, |
|
$(34)$ |
so ist er gleich dem Konvergenzradius $\rho$.
| | | |
| |
| | |
Beispiel: Damit kann der Konvergenzradius der geometrischen Reihe
(16) (den wir ja bereits aus dem Kapitel über Grenzprozesse kennen, ohne ihn dort so genannt zu haben)
noch einmal sehr schön berechnet werden: Da für diese Reihe $a_n=1$ für alle $n$ gilt,
folgt sofort ${a_n\over a_{n+1}}=1$ und damit $\rho=1$.
Existiert der Grenzwert (34) nicht, so lässt sich damit keine Aussage über den Konvergenzradius
machen.
Methode 2: Eine Formel, die immer funktioniert, ist etwas komplizierter und lautet
|
$$\rho = {1\over \limsup\limits_{n\to\infty}\sqrt[n]{|a_n|}}$$
|
, |
|
$(35)$ |
| | | |

geometrische Reihe
| |
| | |
wobei $\rho=\infty$ ist, wenn der Nenner gleich $0$ ist. Das Symbol $\limsup$ im Nenner heißt "Limes Superior" und
wurde im Kapitel über Grenzprozesse kurz besprochen. Er ist der größte
Häufungspunkt der Folge $\langle\sqrt[n]{|a_n|}\rangle$ bzw. wird als $+\infty$ interpretiert, wenn diese Folge
nicht nach oben beschränkt ist. Ist die Folge $\langle\sqrt[n]{|a_n|}\rangle$ konvergent, so stimmt er mit ihrem
Grenzwert überein.
Beispiel: Damit lässt sich zeigen, dass die in der obigen Tabelle angegebene Taylorreihe
der Funktion $x\mapsto\ln(1+x)$ mit Mittelpunkt $0$ den Konvergenzradius $1$ besitzt: Für sie gilt $a_n={(-1)^{n+1}\over n}$, daher
$\sqrt[n]{|a_n|}={1\over \sqrt[n]{n}}$, und da die Folge $\langle\sqrt[n]{n}\rangle$ gegen $1$ konvergiert,
folgt $\rho=1$.
Mit etwas Aufwand können alle in diesem Kapitel angegebenen Konvergenzradien unter Zuhilfenahme dieser beiden Methoden ermittelt werden.
Beispiel: Für die Taylorreihe (12) der Exponentialfunktion gilt $a_n={1\over n!}$.
Nun lässt sich zeigen (was wir hier nicht tun), dass die Folge $\langle\sqrt[n]{n!}\rangle$ nicht nach oben beschränkt ist.
Daher konvergiert die Folge $\langle \sqrt[n]{|a_n|}\rangle$ gegen $0$, und folglich ist $\rho=\infty$, was bedeutet, dass
die Taylorreihe (12) für alle reellen $x$ konvergiert.
Wenn Sie jetzt wissen wollen, woher der Konvergenzradius seinen Namen hat, dann lesen Sie noch den folgenden kurzen
Unterabschnitt!
| | | |

Limes Superior
| |
| | |
Weiterführende Themen
Potenzreihen sind wertvolle Hilfsmittel der Mathematik, deren Auslotung weit über den Stoff, den wir hier behandeln,
hinausführt. Wir wollen hier nur einige knappe Anmerkungen machen.
| | | |
| |
| | |
Zunächst können Potenzreihen auch im Rahmen der komplexen Zahlen betrachtet werden. Formel
funktioniert das, indem für $x$, $x_0$ und die Koeffizienten $a_n$ auch komplexe Zahlen zugelassen sind.
Besonders interessant sind die Konvergenzbereiche, die sich dann ergeben: Sie werden in der komplexen Zahlenebene als Kreise
dargestellt: Sind $x_0$ und alle $a_n$ reell, so ist der
Radius des Konvergenzkreises gleich dem bisher im Reellen betrachteten Konvergenzradius $\rho$,
womit auch erklärt ist, wieso diese Größe
"Radius" genannt wird, und wieso der Konvergenzbereich im Reellen symmetrisch zum Mittelpunkt liegt.
Als Grenzfälle können auch Punkte ($\rho=0$) und die ganze komplexe Ebene ($\rho=\infty$) auftreten.
Beispielsweise kann die geometrische Reihe (16) auch für komplexe Werte von $x$ gebildet werden.
Der Konvergenzbereich dieser Reihe im Komplexen ist dann das Innere der Einheitskreisscheibe der komplexen Zahlenebene
(also der Kreisscheibe mit Mittelpunkt $0$ und Radius $1$), wie die folgende Grafik illustriert:
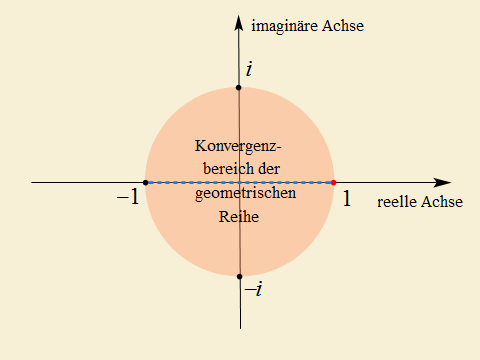
Innerhalb dieses Kreises konvergiert die Potenzreihe gegen $1\over 1-x$ (nun für komplexe $x$ berechnet).
Der rote Punkt stellt die einzige komplexe Zahl dar, an der diese Funktion nicht definiert ist (nämlich $1$), und genau
bis dorthin erstreckt sich die gezeigte Kreisscheibe. Der Konvergenzbereich im Reellen wird durch die strichlierte blaue
Linie dargestellt.
Wird eine Funktion durch eine Potenzreihe gemäß (33) definiert, so erhebt sich die Frage,
ob diese auch außerhalb des Konvergenzbereichs so "fortgesetzt" werden kann, dass insgesamt eine analytische Funktion
entsteht. Man spricht dann von einer analytischen Fortsetzung.
Dies lässt sich in der Regel tatsächlich bewerkstelligen, so beispielsweise, indem die geometrische Reihe
$1+x+x^2+x^3+\dots$,
die nur für $|x| < 1$ konvergiert, zur Funktion $x\mapsto{1\over 1-x}$ forgesetzt wird, die
für alle reellen $x\neq 1$ definiert ist. Eine Methode, dies zu tun, besteht darin,
die Funktion, die durch die Potenzreihe gegeben ist, um einen anderen Mittelpunkt zu entwickeln und dadurch eine
neue Funktion mit einem anderen Konvergenzbereich zu erhalten, der auch Punkte enthält, die nicht im Konvergenzbereich
der ursprünglich gegebenen Potenzreihe liegen. Insbesamt wird auf diese Weise eine Funktion erhalten, die
in einem größeren Bereich definiert ist als zuvor. So kann beispielsweise die geometrische Reihe
im Reellen zu einer Funktion fortgesetzt werden, die auch für $x < -1$ definiert ist, und sie stimmt dort mit
$x\mapsto{1\over 1-x}$ überein. Manchmal muss bei dieser Methode ins Komplexe
"ausgewichen" werden, etwa im Fall der geometrischen Reihe, damit auch Punkte $x > 1$ erreicht werden können.
In manchen Fällen gelingt die analytische Fortsetzung nicht eindeutig, was in das mathematische Gebiet der "mehrwertigen Funktionen"
(zu denen die komplexe Wurzelfunktion und der komplexe Logarithmus zählen) führt.
|
| | |

komplexe Zahlen
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Wir wollen am Ende dieses Kapitels noch eine größere Klasse von Reihen erwähnen, zu denen auch die
Potenzreihen gehören.
Funktionen wie $f(x)={1\over x}$ oder $g(x)={1\over x^2}$ lassen sich nicht in Taylorreihen mit Mittelpunkt $0$ entwickeln,
da sie bei $x=0$ nicht definiert sind. Dennoch besitzt jede von ihnen in der Nähe dieser Stelle ein ganz bestimmtes Verhalten.
Beispielsweise wächst $g(x)$ für $x\to 0$ schneller an als $f(x)$. Um ganz allgemein das Verhalten von Funktionen an isolierten Stellen,
an denen sie nicht definiert sind, in den Griff zu bekommen und miteinander vergleichen zu können, kann man versuchen,
eine Funktion in Potenzen der Variable $x$ zu entwickeln,
wobei auch negative ganzzahlige Exponenten zugelassen sind. In vielen Fällen
gelingt das auch – eine solche Reihe wird Laurentreihe genannt. Zwei Beispiele sind
|
$${\cos x - 1\over x^5} = -{1\over 2x^3} +{1\over 24x} - {x\over 720} +{x^3\over 40320} -{x^5\over 3628800} +\dots$$
|
|
|
$(36)$ |
und
|
$$x^3 \sin({1\over x}) = \dots + {1\over 362880 x^6} - {1\over 5040 x^4} + {1\over 120x^2} - {1\over 6} +x^2$$
|
. |
|
$(37)$ |
Laurentreihen können – ebenso wie Potenzreihen – auch bezüglich eines anderen Mittelpunkts $x_0$ gebildet
werden. Anstelle von Potenzen $x^n$ (mit positiven und negativen Exponenten $n$)
treten dann Potenzen $(x-x_0)^n$ auf.
| | | |
| |
| | |
Bricht eine Laurentreihe "nach unten" ab, d.h. besitzt sie nur endlich viele Potenzen mit negativen Exponenten,
wie im Beispiel (36), so nennen wir ihren Mittelpunkt eine Polstelle (kurz Pol),
einen Begriff, den Sie wahrscheinlich bereits kennen.
Die Ordnung einer Polstelle (kurz: Ordnung eines Pols) wird durch den kleinsten (d.h. den "negativsten") Exponenten bestimmt.
Im Beispiel (36) ist $x=0$ eine Polstelle dritter Ordnung.
Ganz allgemein besitzt eine Funktion $f$, die in eine Laurentreihe mit Mittelpunkt $x_0$ entwickelt werden kann,
bei $x_0$ einen Pol $n$-ter Ordnung, wenn die Funktion $(x-x_0)^nf (x)$ bei geeigneter Festlegung des Werts an der Stelle $x_0$
analytisch (also in eine Taylorreihe mit Mittelpunkt $x_0$ entwickelbar) ist, $(x-x_0)^{n-1}f(x)$ jedoch nicht.
Dies lässt sich sehr schön am Beispiel (36) erkennen:
${\cos x - 1\over x^5}$ besitzt an der Stelle $x=0$ einen Pol dritter Ordnung, denn aus (36) folgt
$$x^3 {\cos x - 1\over x^5}\equiv {\cos x - 1\over x^2}=-{1\over 2}+{x^2\over 24}+\dots\sf{,}$$
was eine Potenzreihe ist (mit dem Wert $-{1\over 2}$ an der Stelle $0$),
wohingegen die Funktion $x^2 {\cos x - 1\over x^5}\equiv {\cos x - 1\over x^3}$ durch keine Wahl eines Werts an der Stelle $0$
analytisch gemacht werden kann, was der erste Term der Laurentreihe
$$x^2 {\cos x - 1\over x^5}\equiv {\cos x - 1\over x^3}=-{1\over 2x}+{x\over 24}+\dots$$
sehr schön zeigt.
Besitzt eine Laurentreihe, wie im Beispiel (37), unendlich viele Potenzen mit negativen Exponenten,
so wird ihr Mittelpunkt eine wesentliche Singularität
genannt.
Auf diese Weise helfen Laurentreihen, das Verhalten von Funktionen in der Nähe von
Unendlichkeitsstellen zu klassifizieren.
| | | |

Polstellen und ihre
Ordnungen
| |
| | |
Der Begriff der Laurentreihe ist auch bei der Klassifiktion von Nullstellen nützlich:
Kann die Funktion $f$ in eine Taylorreihe mit Mittelpunkt $x_0$ entwickelt werden, und gilt $f(x_0)=0$, so nennen wir
$x_0$ eine Nullstelle der Ordnung $m$ (ein Begriff, der für Polynome bereits früher besprochen wurde),
wenn $f(x)\over(x-x_0)^m$ bei geeigneter Festlegung des Werts an der Stelle $x_0$
analytisch (also ebenfalls in eine Taylorreihe mit Mittelpunkt $x_0$ entwickelbar) ist, während $f(x)\over(x-x_0)^{m+1}$
zwar als Laurentreihe mit Mittelpunkt $x_0$, nicht aber als Tayloreihe darstellbar ist.
Beispielsweise besitzt $x^2\sin x$ bei $x=0$ eine Nullstelle dritter Ordnung,
da ${x^2\sin x\over x^3}\equiv {\sin x\over x}$, wie (24) zeigt, analytisch ist, hingegen
$${x^2\sin x\over x^4}\equiv {\sin x\over x^2}={1\over x}-{x\over 6}+\dots$$
wegen des $1\over x$-Terms nicht.
|
| | |

Nullstellen von
Polynomen
und ihre Ordnungen
| |