| | |
| | | |
| |
| | |
| | | |
| |
| | |
Ein Vektor ist eine Liste von Zahlen. In diesem Kapitel werden wir nur reelle Vektoren betrachten, d.h.
Listen von reellen Zahlen.
Damit können mehrere Zahlen zu einem mathematischen Objekt zusammengefasst werden
- eine praktische Angelegenheit. Ein Vektor kann
- ebenso wie eine Zahl -
einen Buchstaben oder ein anderes Symbol als Namen bekommen. Um einem Symbol gleich anzusehen, ob es für einen
Vektor steht, ist es üblich, dafür eine eigene Schreibweise zu verwenden.
Mehrere Konventionen sind gebräuchlich, vor allem:
Kennzeichnung durch einen Pfeil, durch Fettdruck oder durch eine Unterstreichung.
Je nach der verwendeten Schreibweise bezeichnet dann
einen Vektor. Die Pfeildarstellung ist auf Webseiten aus technischen Gründen nicht allzu günstig,
weshalb wir uns für den Fettdruck entscheiden. Ein Beispiel für einen Vektor ist
Wollen wir ihm den Namen a geben, so schreiben wir:
Seine Eintragungen, die Zahlen
3, -2
und 4, nennen wir seine Komponenten und nummerieren sie durch:
Die erste Komponente dieses Vektors ist 3, die zweite
ist -2, usw.
Da wir seine Komponenten nebeneinander geschrieben haben, sprechen wir von einem Zeilenvektor.
Wir können die Eintragungen eines Vektors auch untereinander schreiben, beispielsweise
| | | |

reelle Zahlen
| |
| | |
und nennen ihn dann einen Spaltenvektor. In diesem Kapitel werden wir zwischen Zeilen- und Spaltenvektoren
nicht unterscheiden - welche Form bevorzugt wird, ist eine Sache der Bequemlichkeit
(Zeilenvektoren lassen sich auf Webseiten leichter anschreiben, während Spaltenvektoren, wie wir sehen werden, günstiger zum Rechnen
sind).
Vektoren, die zwei Eintragungen besitzen, wie beispielsweise (4), heißen zweikomponentige (auch zweidimensionale) Vektoren.
Vektoren, die drei Eintragungen besitzen, wie beispielsweise (3), heißen dreikomponentige (auch dreidimensionale) Vektoren.
Ganz allgemein nennen wir
Vektoren, die n Eintragungen besitzen, n-komponentige
oder n-dimensionale Vektoren.
Ein Spezialfall ist n = 1:
Ein "einkomponentiger" oder "eindimensionaler" Vektor ist eine Zahl. Im Rahmen der Vektorrechnung ist es üblich, Zahlen
als Skalare zu bezeichnen. Das hat einen geometrischen Grund, auf den wir unten
zu sprechen kommen.
| | | |
Zur
von Spaltenvektoren
| |
| | |
Wir werden Vektoren in diesem und in einem Nachfolgekapitel vor allem als Werkzeuge kennen lernen, werden besprechen,
wie sie geometrisch gedeutet werden können und wie man mit ihnen rechnen kann.
|
| | |

Vektoren 2
| |
| | |
| Geometrische Deutung von Vektoren |
| | | |
Zum Seitenanfang | |
| | |
In einem früheren Kapitel haben wir die Zeichenebene
mit einem Koordinatensystem ausgestattet. Es hat uns erlaubt,
Punkte mit (geordneten) Zahlenpaaren zu identifizieren.
Üblicherweise werden die Koordinatenachsen bzw. die zugehörigen Koordinaten mit den Buchstaben
x und y
(manchmal auch x1 und x2)
bezeichnet. Die Zeichenebene selbst kann dann als Menge aller reellen
Zahlenpaare, genannt R2,
aufgefasst werden.
| | | |

Koordinaten

Zeichenebene als R 2 2
| |
| | |
Auch der (dreidimensionale) Raum kann mit einem Koordinatensystem
ausgestattet werden: Legen Sie ein Blatt Papier mit eingezeichneter
x- und y-Achse
vor sich auf einen Tisch und denken Sie sich eine dritte, die z-Achse,
normal auf die beiden anderen durch den Ursprung (mit positiver Richtung nach oben) in den Raum gelegt.
Auf diese Weise kann durch die Angabe dreier Zahlen x,
y und z
(manchmal auch als x1, x2 und x3
bezeichnet) die Lage eines Punktes im Raum eindeutig festgelegt werden:
x und y
legen zunächst einen Punkt in der xy-Ebene,
die durch das Blatt Papier dargestellt wird, fest. Dieser Punkt wird dann um den Wert z
"gehoben" (bzw., wenn z < 0 ist, "gesenkt").
Umgekehrt bekommt auf diese Weise jeder Punkt des Raumes drei Koordinaten, und wir können
den Raum selbst als Menge aller (geordneten) reellen
Zahlentripel, genannt R3, auffassen.
Dank dieser Konstruktionen besitzen zwei- und dreikomponentige Vektoren anschauliche geometrische Deutungen.
Zweikomponentige Vektoren
| | | |

Zahlenpaare und Zahlentripel
| |
| | |
Zweikomponentige Vektoren können geometrisch durch Pfeile in der Ebene dargestellt werden. Betrachten wir als Beispiel den Vektor
Wir
 können irgendeinen Punkt der Zeichenebene wählen und von diesem aus
soweit in die x-Richtung gehen, wie die
erste Komponente angibt, und soweit in die y-Richtung, wie die
zweite Komponente angibt. In unserem Beispiel heißt das:
"5 nach rechts, 3 nach oben gehen".
Den Ausgangspunkt nennen wir Schaft, den Zielpunkt Spitze.
Da der Ausgangspunkt beliebig ist, stellt das Zahlenpaar
(5, 3)
jeden Pfeil dar, der auf diese Weise entsteht. In der Skizze rechts haben wir zwei solcher
Pfeile für verschiedene Ausgangspunkte gezeichnet. Jeder der beiden Pfeile
wird vom selben Vektor, nämlich (5) dargestellt.
können irgendeinen Punkt der Zeichenebene wählen und von diesem aus
soweit in die x-Richtung gehen, wie die
erste Komponente angibt, und soweit in die y-Richtung, wie die
zweite Komponente angibt. In unserem Beispiel heißt das:
"5 nach rechts, 3 nach oben gehen".
Den Ausgangspunkt nennen wir Schaft, den Zielpunkt Spitze.
Da der Ausgangspunkt beliebig ist, stellt das Zahlenpaar
(5, 3)
jeden Pfeil dar, der auf diese Weise entsteht. In der Skizze rechts haben wir zwei solcher
Pfeile für verschiedene Ausgangspunkte gezeichnet. Jeder der beiden Pfeile
wird vom selben Vektor, nämlich (5) dargestellt.
Auf diese Weise kann jeder zweikomponentige Vektor durch Pfeile
dargestellt werden. Ist eine seiner Komponenten negativ, so wird vom Schaft in die entgegengesetzte Richtung
(nach links bzw. nach unten) gegangen, ist eine Komponente
0, wird der entsprechende Zug ausgelassen.
Da die zweikomponentigen Vektoren so schön in die Zeichenebene passen, nennt man sie auch
ebene Vektoren.
| | | |
| |
| | |
Wichtig ist, dass ein Vektor nicht nur einem Pfeil entspricht, sondern vielen.
Ein Pfeil in der Zeichenebene ist durch drei Dinge eindeutig bestimmt: seinen Ausgangspunkt (Schaft),
die Richtung, in die er zeigt, und seine Länge. Alle Pfeile, die einen
gegebenen Vektor darstellen, zeigen in die selbe Richtung und sind gleich lang. Sie unterscheiden sich
nur durch den Ort ihres Schafts. In der Praxis zeigen wir oft auf einen konkreten Pfeil
und nennen ihn einen Vektor. Genau genommen ist das eine schlampige Bezeichnung. Der Einfachheit
halber gönnen wir sie uns, sollten aber nicht vergessen, dass auch alle anderen
Pfeile derselben Richtung und Länge zum gleichen Vektor gehören.
Manchmal wird das so ausgedrückt, dass ein Pfeil ein Repräsentant für einen
Vektor (nicht aber mit diesem identisch) ist.
Daraus ergeben sich drei weitere nützliche Deutungen:
- Als
 Verbindungsvektor: Sind zwei Punkte P
und Q gegeben, so legen sie einen Pfeil
fest, indem P als Schaft und
Q als Spitze interpretiert wird.
Dieser Pfeil (genauer: der Vektor, der zu diesem Pfeil gehört) heißt
Verbindungsvektor von P nach
Q
(oder einfach Vektor von P nach
Q
Verbindungsvektor: Sind zwei Punkte P
und Q gegeben, so legen sie einen Pfeil
fest, indem P als Schaft und
Q als Spitze interpretiert wird.
Dieser Pfeil (genauer: der Vektor, der zu diesem Pfeil gehört) heißt
Verbindungsvektor von P nach
Q
(oder einfach Vektor von P nach
Q )
und wird mit dem Symbol )
und wird mit dem Symbol
bezeichnet. Können wir die Komponenten des Verbindungsvektors berechnen, wenn
die Koordinaten der beiden Punkte gegeben sind? Gewiss können wir das, und es ist gar nicht so schwierig:
Schauen Sie sich die obige Skizze genauer an! Ist
| P(p1, p2) und Q(q1, q2) |
, |
|
(6) |
so ist der Verbindungsvektor von P nach
Q durch
| ® |
= |
(q1 - p1, q2 - p2) |
|
| PQ |
|
(7) |
gegeben. Das ist eine einfache, aber wichtige Regel. Sie ist es wert, auswendig gemerkt zu werden!
In Worten lautet sie: Man subtrahiere die Koordinaten des Schaftes von jenen der Spitze.
Sie gilt für beliebige Punkte P
und Q.
Nennen wir sie die "Spitze minus Schaft"-Regel.
- Als
 Verschiebungsvektor: Ist ein Vektor a gegeben, so können wir
ihn dazu benutzen, jeden Punkt der Ebene um ein Stück zu verschieben.
Dazu fassen wir einen beliebigen Punkt P
als Schaft auf, hängen einen Pfeil, der den
Vektor darstellt, dran, und verschieben den Punkt bis zur Spitze
P '. Auf diese Weise entsteht eine
Verschiebung (Translation) aller Punkte der Ebene in die gleiche Richtung und
um die selbe Strecke.
Verschiebungsvektor: Ist ein Vektor a gegeben, so können wir
ihn dazu benutzen, jeden Punkt der Ebene um ein Stück zu verschieben.
Dazu fassen wir einen beliebigen Punkt P
als Schaft auf, hängen einen Pfeil, der den
Vektor darstellt, dran, und verschieben den Punkt bis zur Spitze
P '. Auf diese Weise entsteht eine
Verschiebung (Translation) aller Punkte der Ebene in die gleiche Richtung und
um die selbe Strecke.
Jeder Vektor legt genau eine Verschiebung fest, und umgekehrt kann jede
Verschiebung durch einen eindeutig bestimmten Vektor beschrieben werden. Ist
a = (a1, a2),
so besteht die Wirkung der Verschiebung darin, jeden Punkt
P(p1, p2)
in den Punkt
P '(p1 + a1, p2 + a2)
überzuführen. Berechnen wir zur Kontrolle mit Hilfe der Regel (7) den Verbindungsvektor
von P nach P ':
Es ergibt sich (a1, a2),
was genau der
Vektor a ist.
- Als
 Ortsvektor:
Da die Lage eines Punktes in der Zeichenebene durch ein Zahlenpaar (seine Koordinaten) bestimmt ist, und da
ein zweikomponentiger Vektor ebenfalls ein Zahlenpaar ist, können wir
Komponenten mit Koordinaten und daher
Vektoren mit Punkten identifizieren:
Dem Punkt A(a1, a2)
entspricht der Vektor A = (a1, a2)
und umgekehrt. Vektoren in dieser Eigenschaft heißen Ortsvektoren (da sie einen Ort angeben).
Im Gegensatz dazu wird ein Verbindungsvektor (ein bisschen schlampig) auch Richtungsvektor genannt
(da seine Hauptaufgabe oft darin besteht, eine Richtung anzugeben, aber keinen Ort).
Ortsvektor:
Da die Lage eines Punktes in der Zeichenebene durch ein Zahlenpaar (seine Koordinaten) bestimmt ist, und da
ein zweikomponentiger Vektor ebenfalls ein Zahlenpaar ist, können wir
Komponenten mit Koordinaten und daher
Vektoren mit Punkten identifizieren:
Dem Punkt A(a1, a2)
entspricht der Vektor A = (a1, a2)
und umgekehrt. Vektoren in dieser Eigenschaft heißen Ortsvektoren (da sie einen Ort angeben).
Im Gegensatz dazu wird ein Verbindungsvektor (ein bisschen schlampig) auch Richtungsvektor genannt
(da seine Hauptaufgabe oft darin besteht, eine Richtung anzugeben, aber keinen Ort).
Zur Bezeichnungsweise: Im Sinne einer transparenten Notation ist es günstig (aber nicht unbedingt notwendig), für einen Punkt
und seinen Ortsvektor denselben Buchstaben zu verwenden. In der von uns verwendeten Schreibweise erkennen wir
durch den Fettdruck, dass A als Vektor gemeint
ist, während A für den Punkt steht.
(Es gibt aber auch eine großzügigere Konvention, in der nicht einmal dieser Unterschied gemacht
werden muss). Der Klarheit halber werden wir Punkte immer mit Großbuchstaben
und die zugehörigen Ortsvektoren mit den entsprechenden fettgeduckten Großbuchstaben bezeichnen.
Der Ortsvektor A eines Punktes A lässt sich als
spezieller Verbindungsvektor deuten:
wobei O für den Ursprung steht. Ortsvektoren sind also nichts anderes als
Pfeile, deren Schaft der Ursprung ist. Dank dieser Deutung kann die Menge aller (zweikomponentigen) Vektoren mit der Zeichenebene,
d.h. R2, identifiziert werden.
| | | |

R 2 2
| |
| | |
Manchmal wird anstelle eines "allgemeinen" Punktes (x, y)
dessen Ortsvektor x = (x, y),
auch Radiusvektor genannt, verwendet.
So können wir etwa die x-Achse als
"Menge aller x, deren zweite Komponente
0 ist" auffassen.
Ein anderes Beispiel (das Sie ignorieren können, falls Sie den Funktionsbegriff noch nicht kennen): Es ist bequem, eine Funktion in zwei Variablen
als f º f(x)
anstelle der längeren Form
f º f(x, y)
anzuschreiben. In diesem Sinn stellt die Größe x
zwei Variable gleichzeitig dar.
Alle drei Deutungen haben ihre Berechtigung. Insbesondere die erste und die dritte werden sich beim Rechnen als
besonders nützlich herausstellen.
| | | |

Funktionen in
mehreren Variablen
| |
| | |
Ein besonderer Vektor ist
Er heißt Nullvektor und kann (im Sinne der drei Deutungen) folgendermaßen interpretiert werden:
- als Verbindungsvektor eines Punktes mit sich selbst,
- als Spezialfall einer Verschiebung, die jeden Punkt dort belässt, wo er ist, oder
- als Ortsvektor des Ursprungs.
Manchmal wird für ihn schlampigerweise 0
statt 0 geschrieben.
(In diesem Fall sollte man zumindest wissen, dass nicht die Zahl
0 gemeint ist, sondern der Vektor, dessen Komponenten alle
0 sind).
Da Vektoren mit Richtungen zu tun haben,
werden sie auch gerichtete Größen genannt.
Hingegen sind Skalare (d.h. Zahlen) ungerichtete Größen.
Die in der Vektorrechnung gebräuchliche Bezeichnung "Skalare" dient dazu, den Charakter der Zahlen als
"ungerichteter Größen" hervorzuheben.
Dreikomponentige Vektoren
| | | |
| |
| | |
In drei Dimensionen funktioniert alles bisher Gesagte in ganz analoger Weise, wobei nun die Tatsache benutzt wird, dass
die Lage eines Punktes im Raum durch die Angabe dreier Koordinaten eindeutig festgelegt ist.
Ein Vektor wie
wird durch Pfeile (die alle in dieselbe räumliche Richtung zeigen und dieselbe Länge haben) dargestellt.
Wieder sprechen wir von Schaft und Spitze.
Dreikomponentige Vektoren werden auch räumliche Vektoren genannt. Auch sie
besitzen drei geometrische Deutungen:
- Als Verbindungsvektor:
Ist
| P(p1, p2, p3) und Q(q1, q2, q3) |
, |
|
(11) |
so ist der Verbindungsvektor von P nach
Q durch
| ® |
= |
(q1 - p1, q2 - p2, q3 - p3) |
|
| PQ |
|
(12) |
gegeben (eine weitere "Spitze minus Schaft"-Regel). Ein Verbindungsvektor wird
(ein bisschen schlampig) auch Richtungsvektor genannt
(da seine Hauptaufgabe oft darin besteht, eine Richtung anzugeben).
- Als Verschiebungsvektor: Ist
a = (a1, a2, a3),
so besteht die Wirkung der Verschiebung darin, jeden Punkt
P(p1, p2, p3)
in den Punkt
P '(p1 + a1, p2 + a2, p3 + a3)
überzuführen.
Als Kontrolle ergibt sich mit Hilfe der Regel (12) der Verbindungsvektor
von P nach P '
zu (a1, a2, a3),
was genau der Vektor a ist.
- Als Ortsvektor:
Dem Punkt A(a1, a2, a3)
entspricht der Vektor A = (a1, a2, a3)
und umgekehrt. Auch in diesem Fall verwenden wir die Konvention, dass der Ortsvektor eines Punktes
mit dem selben (Groß-)Buchstaben in Fettdruck bezeichnet wird.
Der Ortsvektor A eines Punktes A lässt sich als
spezieller Verbindungsvektor deuten:
wobei O für den Ursprung steht. Dank dieser Deutung kann die Menge aller (dreikomponentigen) Vektoren mit dem
(dreidimensionalen) Raum, d.h. R3, identifiziert werden.
| | | |

R 3 3
| |
| | |
Anstelle eines "allgemeinen" Punktes (x, y, z)
kann dessen Ortsvektor x = (x, y, z),
auch Radiusvektor genannt, verwendet werden.
So können wir etwa die xy-Ebene als
"Menge aller x, deren dritte Komponente
0 ist" auffassen.
Ein anderes Beispiel (das Sie ignorieren können, falls Sie den Funktionsbegriff noch nicht kennen):
Es ist bequem, eine Funktion in drei Variablen als f º f(x)
anstelle der längeren Form
f º f(x, y, z)
anzuschreiben. In diesem Sinn stellt die Größe x drei Variable gleichzeitig dar.
Der dreikomponentige Nullvektor
kann analog zum zweikomponentigen (9) interpretiert werden. Auch im dreikomponentigen Fall werden
Vektoren als gerichtete Größen,
Skalare (d.h. Zahlen) als ungerichtete Größen bezeichnet.
n-komponentige Vektoren
| | | |

Funktionen in
mehreren Variablen
| |
| | |
Es ist wohl keine Überraschung, dass das bisher Besprochene auch mit
n-komponentigen
Vektoren funktioniert, und dass die gleichen Begriffe verwendet werden wie im
zwei- und dreikomponentigen Fall.
Dass uns in höheren Dimensionen die geometrische Anschauung im Stich lässt,
kann uns nicht daran hindern, Vektoren wie
anzuschreiben. Stellen Sie sich etwa vor, sechs (durchnummerierte) meteorologische Stationen messen
zu einer bestimmten Zeit die Lufttemperatur. Ihre Daten (in Grad Celsius) könnten dann
einem derartigen Vektor entsprechen. Auf diese Weise wird ein ganzer Datensatz
in Form eines einzigen mathematischen Objekts dargestellt.
Die zu einem anderen Zeitpunkt gewonnenen Messdaten werden dann durch
einen anderen sechskomponentigen Vektor dargestellt.
Auch für n-komponentige Vektoren sind die
drei Deutungen (als Verbindungs, Verschiebungs- und Ortsvektor) möglich, und
die Menge aller (n-komponentigen) Vektoren kann mit dem
n-dimensionalen Raum,
d.h. R n,
der Menge aller "n-Tupel"
( n,
der Menge aller "n-Tupel"
( = = Listen aus n Zahlen) identifiziert
werden. Um beim Temperaturbeispiel zu bleiben, stellt der durch (15)
definierte Datensatz (in einem formalen Sinn) einen "Punkt" in einem sechsdimensionalen Raum
dar. Listen aus n Zahlen) identifiziert
werden. Um beim Temperaturbeispiel zu bleiben, stellt der durch (15)
definierte Datensatz (in einem formalen Sinn) einen "Punkt" in einem sechsdimensionalen Raum
dar.
|
| | |

R n n
| |
| | |
| Rechenoperationen für Vektoren |
| | | |
Zum Seitenanfang | |
| | |
Wir definieren nun zwei Rechenoperationen für Vektoren: das Bilden des Vielfachen und der Summe.
- Bilden des Vielfachen eines Vektors (oder Multiplikation eines Vektors mit einem Skalar):
Sei c ein Skalar, d.h. eine reelle Zahl.
Von jedem Vektor kann das c-fache gebildet
werden, indem alle seinen Komponenten mit c
multiplitziert werden. Das c-fache des
Vektors a bezeichnen wir als
c
 a.
(So ist etwa
2a
das Doppelte von a).
Für einen zweikomponentigen Zeilenvektor sieht das so a.
(So ist etwa
2a
das Doppelte von a).
Für einen zweikomponentigen Zeilenvektor sieht das so
c (a1, a2) = (c a1, c a1, c a2) a2) |
|
|
(16) |
und für einen dreikomponentigen Spaltenvektor so
| c |
⎛ |
b1 |
⎞ |
= |
⎛ |
c b1 b1 |
⎞ |
|
| ⎜ |
b2 |
⎟ |
⎜ |
c b2 b2 |
⎟ |
| ⎝ |
b3 |
⎠ |
⎝ |
c b3 b3 |
⎠ |
|
(17) |
aus. Für c ¹ 0 schreiben wir
anstelle von c-1a
auch
a/c.
- Bilden der Summe zweier Vektoren gleichen Typs (Vektoraddition): Von zwei Vektoren mit gleich vielen Komponenten
kann die Summe gebildet werden, indem die einander entsprechenden Komponenten addiert werden.
Beispielsweise sieht das für zwei zweikomponentige Zeilenvektoren so
| (a1, a2) + (b1, b2) = (a1 + b1, a2 + b2) |
. |
|
(18) |
und für zwei dreikomponentige Spaltenvektoren so
| ⎛ |
c1 |
⎞ |
+ |
⎛ |
d1 |
⎞ |
= |
⎛ |
c1
+ d1 |
⎞ |
|
| ⎜ |
c2 |
⎟ |
⎜ |
d2 |
⎟ |
⎜ |
c2
+ d2 |
⎟ |
| ⎝ |
c3 |
⎠ |
⎝ |
d3 |
⎠ |
⎝ |
c3
+ d3 |
⎠ |
|
(19) |
aus.
Beide Operationen werden komponentenweise ausgeführt, d.h. für jede Komponente extra.
Das hat zwei wichtige Konsequenzen:
Erstens lässt sich in der Schreibweise mit Spaltenvektoren
einfacher rechnen (insbesondere, was die Summe betrifft, da die zu addierenden Zahlen, wie in (19)
ersichtlich, bereits nebeneinander stehen). Verwenden Sie beim Rechnen immer die Ihnen angenehmere
Schreibweise!
| | | |
| |
| | |
Zweitens gelten die Rechengesetze, die wir vom Umgang mit Zahlen kennen, hier in
gleicher Weise (mit der Ausnahme, dass nicht durch einen Vektor dividiert werden darf).
Wir bezeichnen sie mit ihren mathematischen Fachbegriffen:
- Assoziativgesetz der Multiplikation mit einem Skalar: c(k
 a) = (ck) a) = (ck) a. a.
- Multiplikation mit der Zahl 1: 1
 a = a a = a
- Multiplikation mit der Zahl 0: 0
 a = 0 a = 0
- Kommutativgesetz der Vektoraddition: a + b = b + a
- Assoziativgesetz der Vektoraddition: (a + b) + c = a + (b + c)
- Addition des Nullvektors: a + 0 = a
- Distributivgesetze:
c(a + b) = c
 a + c a + c b,
(c + k) b,
(c + k) a = c a = c a + k a + k a a
- Das Negative eines Vektors a
ist (-1)
 a
und wird als
- a
und wird als
- a
bezeichnet. Berechnet wird es komponentenweise, indem von jeder Komponente des Vektors
a das Negative gebildet wird. a
bezeichnet. Berechnet wird es komponentenweise, indem von jeder Komponente des Vektors
a das Negative gebildet wird.
- Die Differenz zweier Vektoren (d.h. die Rechenoperation der Subtraktion) ist durch
a - b = a +
 (- (- b)
definiert. Berechnet wird sie komponentenweise: Die Komponenten der Differenz sind die Differenzen der Komponenten. b)
definiert. Berechnet wird sie komponentenweise: Die Komponenten der Differenz sind die Differenzen der Komponenten.
| | | |

Zahlen
| |
| | |
Diese Rechenoperationen sind zunächst rein formal gemeint. Sie müssen nicht für jede Anwendung
des Vektorbegriffs eine sinnvolle Bedeutung haben.
Stellt etwa, wie oben besprochen, der Vektor (15)
die zu einer bestimmten Zeit von sechs meteorologischen Stationen ermittelten Temperaturwerte dar,
so macht es nicht viel Sinn, Vielfache dieser Temperaturen zu bilden.
Ist aber b ein anderer
derartiger Temperaturvektor (der einer späteren Messzeit entspricht),
so kann es durchaus sinnvoll sein, die Differenz
b - a
zu bilden. Sie fasst die Temperaturänderungen der einzelnen Stationen zu einem einzigen Datensatz zusammen.
Der Summe a + b wiederum
wird keine besondere Bedeutung beizumessen sein (was wäre die Summe zweier Temperaturen?), wohingegen der Vektor
(a + b)/2
die Mittelwerte der sechs Stationen aus zwei hintereinanderfolgenden Messungen enthält und als solcher wieder eine
sinnvolle Größe ist.
| | | |

Mittelwert
(in Vorbereitung)
| |
| | |
Eine besonders anschauliche und nützliche Bedeutung erlangen die Rechenoperationen
in geometrischen Zusammenhängen, d.h. wenn Vektoren, wie oben
besprochen, geometrisch gedeutet werden. Diesem Thema wenden wir uns nun zu und werden es bis zum Ende
des Kapitels beibehalten.
|
| | |
| |
| | |
| Geometrische Bedeutung der Rechenoperationen |
| | | |
Zum Seitenanfang | |
| | |
In diesem Abschnitt werden wir die geometrische Bedeutung der zuvor definierten Rechenoperationen
besprechen und eine Reihe von Anwendungsmöglichkeiten entdecken.
Vielfaches
Sei
 a ein Vektor und c
ein Skalar. Dann sind, wie oben definiert und in (16) und (17) illustriert, die Komponenten von
c
a ein Vektor und c
ein Skalar. Dann sind, wie oben definiert und in (16) und (17) illustriert, die Komponenten von
c a
das c-fache der Komponenten von a.
Wie kommen wir von einem Pfeil, der a darstellt,
zu einem Pfeil, der c a
das c-fache der Komponenten von a.
Wie kommen wir von einem Pfeil, der a darstellt,
zu einem Pfeil, der c a
darstellt? a
darstellt?
- Ist c > 0,
dann wird der a-Pfeil
um den Faktor c
aufgeblasen (falls c > 1)
oder geschrumpft (falls c < 1).
- Ist c < 0,
so wird der a-Pfeil um den Faktor
|
 c|
aufgeblasen bzw. geschrumpft, und es kommt noch eine Richtungsumkehr dazu. c|
aufgeblasen bzw. geschrumpft, und es kommt noch eine Richtungsumkehr dazu.
In der Skizze ist das anhand des ebenen Vektors
a = (3, 1)
und seiner Vielfachen
2a = (6, 2)
und
- a = (-3, -1)
illustriert. a = (-3, -1)
illustriert.
Des Vektor c a
hat daher folgende geometrische Bedeutung: a
hat daher folgende geometrische Bedeutung:
- Seine Länge beträngt das |
 c|-fache
der Länge von a.
(Mit der Länge eines Vektors werden wir uns weiter unten noch genauer beschäftigen). c|-fache
der Länge von a.
(Mit der Länge eines Vektors werden wir uns weiter unten noch genauer beschäftigen).
- Je nach dem Vorzeichen von c zeigt er in die gleiche oder in die
entgegengesetzte Richtung wie a (ist in jedem Fall
aber parallel zu a).
| | | |
| |
| | |
Genau genommen liegt
diesen Aussagen die Tatsache zu Grunde, dass beim "Aufblasen" und "Schrumpfen" einer geometrischen Figur alle
Längenverhältnisse unverändert bleiben. Mit diesen Dingen
(der Ähnlichkeit von Figuren) wollen wir uns in einem anderen Kapitel näher beschäftigen.
Dass alle Vielfachen eines Vektors in die gleiche (oder entgegengesetzte) Richtung zeigen wie er selbst,
formalisieren wir so:
Definition: Wir nennen zwei Vektoren (zueinander) parallel (oder kollinear),
wenn einer von beiden ein Vielfaches des anderen ist.
Die Parallelität zweier Vektoren kann abgekürzt in der Form
a || b
ausgedrückt werden.
Beachten Sie die Konsequenzen dieser Definition:
- Zwei Vektoren, von denen (zumindest) einer 0
ist, gelten als zueinander parallel.
Diese Feinheit ist in der Rechenpraxis nicht bedeutsam, aber aus formalen Gründen günstig.
- Zwei von 0 verschiedene Vektoren
a und b
sind genau dann zueinander parallel, wenn sie Vielfache voneinander sind
(d.h. wenn es einen Skalar c ¹ 0 gibt, so dass
a = c
 b,
daher auch
b = a/c). b,
daher auch
b = a/c).
- Auch zwei Vektoren, die in entgegengesetzte Richtungen zeigen
(also negative Vielfache voneinander sind), werden als zueinander parallel bezeichnet.
(Nach einer anderen Konvention heißen solche Vektoren antiparallel).
Alles, was wir hier über Vielfache eines Vektors gesagt haben, gilt
auch für räumliche Vektoren.
In formaler Hinsicht gilt es auch in höheren Dimensionen, obwohl uns
dort die Anschauung nicht mehr hilft.
Summe
| | | |

Ähnlichkeit
| |
| | |
Was bedeutet die Addition zweier Vektoren geometrisch? Die Addition zweier positiver Zahlen
a und b können wir uns
vorstellen als das "Aneinanderlegen" (von links nach rechts) zweier Strecken der Längen a und b.
Die Summe a + b entspricht dann der
Gesamtlänge der beiden Strecken. Für negative Zahlen müssen wir diese Regel leicht
ändern: So entspricht einem negativen b eine
Strecke der Länge | b|,
die bei der Addition "nach links" angelegt wird. Nichts anderes geschieht bei der Vektoraddition,
die wir oben formal definiert und durch (18) und (19) illustriert haben: b|,
die bei der Addition "nach links" angelegt wird. Nichts anderes geschieht bei der Vektoraddition,
die wir oben formal definiert und durch (18) und (19) illustriert haben:
Seien
 a und b Vektoren,
gedeutet als Pfeile. Wir legen sie so aneinander ("hintereinander"), dass die Spitze von a
mit dem Schaft von b übereinstimmt.
Die Summe a + b
ist dann der Vektor vom Schaft von a zur
Spitze von b.
Wenn wir mit einem Pfeil die Aufforderung "gehe vom Schaft zur Spitze" verbinden und zwei Pfeile
wie beschrieben aneinanderlegen, so entsprechen sie einem kleinen Spaziergang:
a und b Vektoren,
gedeutet als Pfeile. Wir legen sie so aneinander ("hintereinander"), dass die Spitze von a
mit dem Schaft von b übereinstimmt.
Die Summe a + b
ist dann der Vektor vom Schaft von a zur
Spitze von b.
Wenn wir mit einem Pfeil die Aufforderung "gehe vom Schaft zur Spitze" verbinden und zwei Pfeile
wie beschrieben aneinanderlegen, so entsprechen sie einem kleinen Spaziergang:
- a sagt:
"Gehe von meinem Schaft bis zu meiner Spitze".
- Sind wir dort angelangt, sagt b:
"Gehe von meinem Schaft bis zu meiner Spitze".
Die Summe der beiden Vektoren entspricht dann der Aufforderung, den Spaziergang abzukürzen, um Umwege
zu vermeiden: "Gehe vom Schaft von a zur
Spitze von b".
In der Skizze ist das für die beiden Vektoren
a = (1, 4)
und
b = (3, -2),
deren Summe
a + b = (4, 2)
ist, illustriert. Studieren Sie sie genauer, um nachzuvollziehen, wie die Komponenten
(4, 2) der Summe
zustandekommen!
Ein derartiges Verhalten von Pfeilen ist in der Physik bei Geschwindigkeiten und Kräften bekannt
(die beide "gerichtete Größen" sind und durch Vektoren beschrieben werden).
Die Summe zweier Vektoren wird dort die resultierende (Geschwindigkeit bzw. Kraft)
genannt.
In der Deutung von Pfeilen als Verbindungsvektoren kann die Vektoraddition
durch die allgemeine Regel
charakterisiert werden. Sie gilt für beliebige Punkte
A, B und C.
Eine
 interessante geometrische Deutung besitzt die Rechenregel
a + b = b + a
(das Kommutativgesetz der Vektoraddition):
Beginnen wir an einem beliebigen Punkt.
Nach unserer Regel interpretieren wir a + b,
indem wir an diesen Punkt zuerst (den Schaft von) a
anlegen, und danach an die Spitze von a den Schaft von
b. Dieser markiert das Ende des Spaziergangs.
Um b + a zu
interpretieren, machen wir es genau umgekehrt: Wir legen b
(genauer: einen weiteren Pfeil, der b
repräsentiert) an den Ausgangspunkt und fügen dann
a
(genauer: einen weiteren Pfeil, der a
repräsentiert) hinzu. In beiden Fällen endet der Spaziergang im selben Punkt.
Die Zeichnung dieses Sachverhalts (siehe die nebenstehende Skizze), enthält zwei Pfeile für
a und zwei Pfeile für
b.
Da zwei Pfeile, die vom selben Vektor dargestellt werden, zueinander parallel sind,
schließt sich die entstehende Figur zu einem Parallelogramm.
Das kann dazu benutzt werden, die Summe zweier Vektoren als jenen Pfeil zu definieren, der der
Diagonale dieses Parallelogramms entspricht - ein Gesichtspunkt, der
Parallelogrammregel genannt wird.
interessante geometrische Deutung besitzt die Rechenregel
a + b = b + a
(das Kommutativgesetz der Vektoraddition):
Beginnen wir an einem beliebigen Punkt.
Nach unserer Regel interpretieren wir a + b,
indem wir an diesen Punkt zuerst (den Schaft von) a
anlegen, und danach an die Spitze von a den Schaft von
b. Dieser markiert das Ende des Spaziergangs.
Um b + a zu
interpretieren, machen wir es genau umgekehrt: Wir legen b
(genauer: einen weiteren Pfeil, der b
repräsentiert) an den Ausgangspunkt und fügen dann
a
(genauer: einen weiteren Pfeil, der a
repräsentiert) hinzu. In beiden Fällen endet der Spaziergang im selben Punkt.
Die Zeichnung dieses Sachverhalts (siehe die nebenstehende Skizze), enthält zwei Pfeile für
a und zwei Pfeile für
b.
Da zwei Pfeile, die vom selben Vektor dargestellt werden, zueinander parallel sind,
schließt sich die entstehende Figur zu einem Parallelogramm.
Das kann dazu benutzt werden, die Summe zweier Vektoren als jenen Pfeil zu definieren, der der
Diagonale dieses Parallelogramms entspricht - ein Gesichtspunkt, der
Parallelogrammregel genannt wird.
| | | |

Parallelogramm
| |
| | |
Die Summe von mehr als zwei Vektoren kommt auf analoge Weise zustande. Wir legen die entsprechenden Pfeile (in beliebiger Reihenfolge)
"Schaft an Spitze" aneinander, wie hier in der linken Skizze gezeigt:
Die rechte Skizze illustriert, dass die Summe von Vektoren, die einen zu seinem Ausgangspunkt zurückkehrenden Spaziergang
(das Fachterminus heißt: einen geschlossenen Polygonzug) definieren, 0 ist.
Diese Art, mit Pfeilen zu hantieren, mag Ihnen vielleicht allzu trivial erscheinen. Wir dürfen aber nicht vergessen, dass
all diese Diagramme mit konkreten Rechenvorgängen verbunden sind.
Umgekehrt bedeutet das, dass wir jetzt in die Lage kommen, geometrische Sachverhalte durch Rechnungen analysieren zu
können.
Übungsaufgabe: Man prüfe (durch Rechnen, nicht durch Zeichnen!) nach, ob sich die Vektoren
(1, -3),
(-3, 1)
und (2, 1)
nach Art der Skizze rechts oben zu einem Dreieck zusammenfügen lassen oder nicht!
Lösung: Wir addieren die drei Vektoren:
(1, -3) +
(-3, 1) +
(2, 1) =
(1 - 3 + 2, -3 + 1 + 1) =
(0, -1), was
nicht der Nullvektor ist. Daher schließen sich die drei Vektoren nicht auf die verlangte Weise.
Wir wollen noch erwähnen, dass vom Standpunkt der Deutung von Vektoren als
Verschiebungsvektoren (s.o.) das Bilden der Summe a + b
dem Hintereinander-Ausführen der beiden durch a und b dargestellten
Verschiebungen entspricht.
Alles, was wir hier über Summen von Vektoren gesagt haben, gilt
auch für räumliche Vektoren.
In formaler Hinsicht gelten Sie auch in höheren Dimensionen, obwohl uns
dort die Anschauung nicht mehr hilft.
Differenz
| | | |
| |
| | |
Aus der geometrischen Bedeutung der Summe ergibt sich jene der Differenz zweier Vektoren:
 |
|
 |
Differenz zweier Vektoren:
"Spitze minus Schaft"-Regel |
|
Verbindungsvektor
als Differenz der Ortsvektoren |
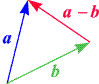
Die linke der beiden Skizzen zeigt die geometrische Bedeutung der Differenz zweier Vektoren
a und b.
Werden die Pfeile wie gezeigt angeordnet, so ergibt sich die Differenz
a - b
als Verbindungsvektor der Spitzen, und zwar so, dass der erste Vektor
(a) die Spitze und der zweite
(b) den Schaft bildet. Hier haben wir eine weitere
Variante der "Spitze minus Schaft"-Regel.
(Beweis: Das Diagramm, anders betrachtet, stellt die Addition zweier Vektoren dar:
b + (a - b) = a).
Die Differenz zweier Vektoren stellt sich hier als Antwort auf die Frage
"b + wieviel ist
a?" dar.
Es ist hilfreich, wenn Sie diese Regel jederzeit anwenden können, ohne sie erst nachschlagen zu müssen.
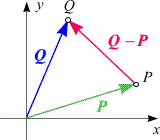
Eine wichtige Konsequenz daraus ergibt sich für die Berechnung von Verbindungsvektoren (siehe die Skizze oben rechts).
Setzen wir für a und b
die Ortsvektoren
Q und P
zweier Punkte Q und P,
so ergibt sich für den Verbindungsvektor von P nach
Q
Beachten Sie die Reihenfolge, in der die beiden Punkte auf der linken und auf der rechten Seite dieser Formel vorkommen!
Sie fasst die in (7) und (12) bereits formulierte
Methode, Verbindungsvektoren zu berechnen, kompakt (und in beliebigen
Dimensionen gültig) zusammen. Sehen Sie sich die genaue Struktur der Formeln
(7) und (12) noch einmal an und vergleichen Sie sie mit
(20)!
Um in geometrischen Skizzen Differenzen zu erkennen, ist es aber auch nützlich, die Identität
a - b = a + (- (- b)
im Gedächtnis zu behalten. Betrachten wir als Beispiel dazu eine b)
im Gedächtnis zu behalten. Betrachten wir als Beispiel dazu eine
Aufgabe:
 Von einem (verdrehten) Quadrat seien,
gemäß der nebenstehenden Skizze, der Punkt
G(56, 23)
und der Vektor
a = (16, -10)
gegeben. Gesucht sind die Koordinaten seines Mittelpunkts M.
Von einem (verdrehten) Quadrat seien,
gemäß der nebenstehenden Skizze, der Punkt
G(56, 23)
und der Vektor
a = (16, -10)
gegeben. Gesucht sind die Koordinaten seines Mittelpunkts M.
Lösung: Um den Ortsvektor von M
zu finden, konstruieren wir ihn zuerst als Summe von Vektoren, indem wir einen kleinen Spaziergang machen:
Wir beginnen am Ursprung, gehen von dort nach G
und folgen dann dem Vektor
- a
(den wir uns mit dem Schaft in G gehängt denken)
bis M.
Daher ist
M = G + a
(den wir uns mit dem Schaft in G gehängt denken)
bis M.
Daher ist
M = G + (- (- a) =
G - a.
Jetzt setzen wir die gegebenen Zahlen ein:
M = (56, 23) - (16, -10) =
(40, 33) und haben damit die Koordinaten von
M bestimmt:
M(40, 33).
Klicken Sie hier, um in der Skizze die Darstellung von M als Summe
an- und abzuschalten! a) =
G - a.
Jetzt setzen wir die gegebenen Zahlen ein:
M = (56, 23) - (16, -10) =
(40, 33) und haben damit die Koordinaten von
M bestimmt:
M(40, 33).
Klicken Sie hier, um in der Skizze die Darstellung von M als Summe
an- und abzuschalten!
Spezielle Linearkombinationen
| | | |
| |
| | |
Eine Linearkombination ist eine Summe von Vielfachen von Vektoren, wie zum Beispiel
a + b oder
2a - 3b + c/2.
Zwei Spezialfälle von Linearkombinationen, die Summe und die Differenz zweier Vektoren haben wir bereits ausführlich besprochen.
Wir wollen uns nun noch einige weitere Linearkombinationen, die eine
interessante geometrische Bedeutung haben, ansehen.
- Halbierungspunkt einer Strecke:
Sind A und B
zwei Punkte (in der Ebene oder im Raum), und ist H
der Halbierungspunkt der Strecke, die A und B
verbindet, so gilt
Versuchen sie, den Beweis selbst zu führen, bevor Sie ihn sich ansehen!
Diese Formel sieht nicht zufällig der für den Mittelwert zweier Zahlen ähnlich
- wir können H tatsächlich als
Mittelwert zweier Vektoren verstehen.
| | | |

Mittelwert
(in Vorbereitung)
| |
| | |
- Streckenteilungen: Seien A und B
zwei Punkte (in der Ebene oder im Raum) und T
ein Punkt auf der Strecke, die A und B
verbindet. Wird die Länge AB durch
T im Verhältnis
AT : TB = m : l
geteilt (l, m > 0),
dann gilt
| T = |
1
l + m |
(l A + m A + m B) B) |
. |
|
(22) |
Für
l = m
ergibt sich als Spezialfall der Halbierungspunkt (21).
Ein Ausdruck der Form (22) kann auch als gewichtetes Mittel zweier Vektoren
verstanden werden.
(Je nach dem Verhältnis von l zu m
tragen A und B
verschieden viel bei, bekommen also verschiedene "Gewichte").
Der Begriff der "Teilung" kann übrigens auf den Fall verallgemeinert werden, dass
l oder m
negativ ist. Dann liegt T zwar auf der Geraden
durch A und B,
aber außerhalb ihrer Verbindungsstrecke (und heißt
äußerer
Teilungspunkt).
| | | |

gewichtetes Mittel
(in Vorbereitung)
| |
| | |
- Schwerpunkt einer Menge von Punkten:
Sind A1,
A2, ...
An
endlich viele Punkte (in der Ebene oder im Raum), so wird ihr Schwerpunkt als
| S = |
1
n |
(A1 + A2 + ... + An) |
|
|
(23) |
definiert.
Ebenso wie der Halbierungspunkt (21) einer Strecke (die sich als Spezialfall für
n = 2 ergibt), kann auch
S als Mittelwert (von n Vektoren)
interpretiert werden. Physikalisch entspricht
S dem Massenmittelpunkt einer endlichen Menge von (gleich schweren) Massenpunkten.
Der Fall n = 3 ist für das
Studium der geometrischen Eigenschaften von Dreiecken (der so genannten Trigonometrie) bedeutsam. Interessanterweise
fällt dann S mit dem Schwerpunkt der durch die
drei Punkte A1, A2 und
A3 definierten Dreiecksfläche
zusammen (physikalisch ausgedrückt: wenn Sie ein homogenes Dreieck in diesem Punkt aufhängen, kippt es nicht)
und wird als Schwerpunkt des Dreiecks bezeichnet.
| | | |

Schwerpunkt
eines Dreiecks
| |
| | |
Beim Anwenden der Vektorrechnung auf geometrische Probleme werden, je nach Aufgabenstellung,
auch andere Linearkombinationen auftreten. Betrachten wir zum Abschluss dieses Abschnitts ein
Beispiel:
 Von einem Parallelogramm sind die Punkte
A(0, 1) und
B(4, 2) sowie der Mittelpunkt
M(3, 4) gegeben. Gesucht sind die
(Koordinaten der) Punkte C und D.
Von einem Parallelogramm sind die Punkte
A(0, 1) und
B(4, 2) sowie der Mittelpunkt
M(3, 4) gegeben. Gesucht sind die
(Koordinaten der) Punkte C und D.
Lösung: Von Vektoren ist in dieser Aufgabe keine Rede, aber wir benutzen sie als Werkzeug, um
schnell ans Ziel zu kommen:
Mit A und M kennen
wir auch den Verbindungsvektor
Da es sich um ein Parallelogramm handelt, ist dieser Vektor mit
identisch. Wenn wir also vom Ursprung nach M
und von dort weiter nach C gehen, kennen
wir alle Vektoren, die auf diesem Weg liegen bzw. können sie leicht berechnen.
Der Ortsvektor von C ist daher durch die Summe
C = M + (M - A) =
2M - A
gegeben. (Hier haben wir die Linearkombination!)
Klicken Sie hier, um in der obigen Skizze
die Vektoren M (blau) und
M - A
(grün) in der Anordnung,
in der wir sie benötigen, anzuzeigen! Jetzt setzen wir die gegebenen Zahlen ein:
C = 2(3, 4) - (0, 1) =
(6, 7).
Damit ist der Punkt C gefunden:
Seine Koordinaten sind (6, 7).
Die analoge Berechnung von D überlassen wir Ihnen.
Bemerkung: Die Aufgabe kann auch auf andere Art gelöst werden, z.B. indem wir vom Ursprung nach
A gehen, von wo aus das Doppelte des Vektors
M - A
nach C führt. Das entspricht der Rechnung
C = A + 2(M - A) =
2M - A,
das Resultat ist klarerweise dasselbe.
Wie das Beispiel zeigt, kann es bei der Anwendung der Vektorrechnung auf geometrische Probleme mehrere Lösungswege geben.
Das Wichtigste ist, dass Sie eine finden. Bei komplizierteren Aufgaben müssen Sie
vielleicht ein bisschen danach suchen. Oft geht es darum, zu erkennen, welche Vektoren in einer Skizze mehrfach
vorkommen. Wenn Sie mit den Grundlagen der Rechenoperationen, wie wir
sie hier besprochen haben, vertraut sind, werden Sie mit der Zeit einen Blick dafür entwickeln.
Lineare (Un-)Abhängigkeit
| | | |
| |
| | |
Wir wollen hier noch kurz zwei Begriffe einführen, die die Frage betreffen, wie "unabhängig"
Vektoren voneinander sind: Wir nennen eine (endliche) Menge von Vektoren linear abhängig,
wenn es möglich
ist, zumindest einen dieser Vektoren als Linearkombination (s.o.) der anderen auszudrücken.
Ist das nicht möglich, so heißen die Vektoren linear unabhängig.
Beispiel: Die drei Vektoren
a = (3, 2, 1),
b = (13, -2, -7) und
c = (-2, 4, 5)
sind linear abhängig, da
b = 3a - 2c.
(Rechnen Sie nach!)
Einige Kriterien für lineare Abhängigkeit:
- In jeder Dimension gilt:
Zwei Vektoren sind linear abhängig, wenn sie zueinander
parallel (kollinear) sind (s.o.).
- Für ebene Vektoren gilt:
Eine Menge von drei ebenen Vektoren ist immer linear abhängig.
- Für räumliche Vektoren gilt:
Drei räumliche Vektoren sind linear abhängig, wenn sie
(als Ortsvektoren aufgefasst) in einer Ebene liegen. (Man nennt sie dann koplanar).
Eine Menge von vier räumlichen Vektoren ist immer linear abhängig.
- Es lässt sich zeigen, dass im R
 n
eine Menge von n + 1 Vektoren
immer linear abhängig ist. n
eine Menge von n + 1 Vektoren
immer linear abhängig ist.
Die Dimension - ein Begriff, der
zumindest in Gestalt der Bezeichnungen "zweidimensional" und "dreidimensional"
intuitiv einleuchtet - kann übrigens formal
definiert werden als die maximale Zahl von Vektoren, die eine linear unabhängige
Menge bilden können. Damit lässt sich zeigen, dass die Dimension des
R n
gerade n
ist. Als Spezialfall n = 1
ergibt sich, dass die Zahlengerade eindimensional ist. n
gerade n
ist. Als Spezialfall n = 1
ergibt sich, dass die Zahlengerade eindimensional ist.
| | | |

Zahlengerade
| |
| | |
Eine genauere und allgemeine Theorie der "Räume" von Vektoren (genannt Vektorräume)
steht erst in einem sehr späten Kapitel auf dem Programm.
| | | |

Vektorraum
(in Vorbereitung)
| |
| | |
Um Ihre Vorstellung an den Umgang mit räumlichen Vektoren zu gewöhnen,
rufen Sie das nebenstehende Applet auf! Sie sehen 3D-Visualisierungen, die
Orts- und Richtungsvektoren sowie die Bildung von Summe und Differenz
zeigen, und die Sie mit der Maus beliebig drehen und von allen Seiten
betrachten können. Zudem können Sie
das Ablesen von Komponenten üben.
|
| | |
Applet
3-Vektoren kennenlernen
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
In der geometrischen Deutung erscheinen Vektoren als Pfeile. Egal, ob als Verbindungs-, Verschiebungs- oder Ortsvektor:
Alle Pfeile, die einen (ebenen oder räumlichen) Vektor a
repräsentieren, haben die gleiche Länge:
- Ist
 a = (a1, a2)
ein ebener Vektor, so ist diese Länge gleich
(a12 + a22)1/2.
Geometrisch betrachtet ist dies die Länge der Diagonale eines Rechtecks mit Seitenlängen
a1 und a2
(siehe nebenstehende Skizze) und folgt unmittelbar aus dem pythagoräischen Lehrsatz.
a = (a1, a2)
ein ebener Vektor, so ist diese Länge gleich
(a12 + a22)1/2.
Geometrisch betrachtet ist dies die Länge der Diagonale eines Rechtecks mit Seitenlängen
a1 und a2
(siehe nebenstehende Skizze) und folgt unmittelbar aus dem pythagoräischen Lehrsatz.
- Ist
a = (a1, a2, a3)
ein räumlicher Vektor, so haben alle ihn repräsentierenden Pfeile die Länge
(a12 + a22 + a32)1/2.
Geometrisch betrachtet ist dies die Länge der Raumdiagonale eines Quaders mit Seitenlängen
a1, a2
und a3.
Sie kann durch zweimalige Anwendung des pythagoräischen Lehrsatzes berechnet werden:
Ist d die Länge der Diagonale
des "Bodenrechtecks" mit Seitenlängen a1 und a2,
so gilt d
 2 = a12 + a22.
Die Raumdiagonale ist dann die Diagonale eines "senkrecht stehenden" Rechtecks mit Seitenlängen
d und a3,
woraus sich obiger Ausdruck ergibt. 2 = a12 + a22.
Die Raumdiagonale ist dann die Diagonale eines "senkrecht stehenden" Rechtecks mit Seitenlängen
d und a3,
woraus sich obiger Ausdruck ergibt.
Diese Erkenntnisse erheben wir zur
Definition des Betrags eines Vektors
| | | |
| |
| | |
Der Betrag eines Vektors, bezeichnet mit demselben Symbol
| | wie der
Absolutbetrag einer Zahl, ist wie folgt definiert: | wie der
Absolutbetrag einer Zahl, ist wie folgt definiert:
- Für einen zweikomponentigen (ebenen) Vektor a = (a1, a2)
legen wir fest
| a a | = (a12 + a22)1/2 | = (a12 + a22)1/2 |
. |
|
(24) |
- Für einen dreikomponentigen (räumlichen) Vektor a = (a1, a2, a3)
legen wir fest
| a a | = (a12 + a22 + a32)1/2 | = (a12 + a22 + a32)1/2 |
. |
|
(25) |
- Allgemein ist der Betrag eines n-komponentigen Vektors a = (a1, a2, ..., an)
definiert durch
| a a | = (a12 + a22 + ... + an2)1/2 | = (a12 + a22 + ... + an2)1/2 |
. |
|
(26) |
| | | |

Absolutbetrag
| |
| | |
In allen Fällen gilt: Der Betrag eines Vektors ist die Wurzel aus der Summe der Quadrate seiner Komponenten.
Er gehorcht einem Rechengesetz, das sofort aus seiner Definition folgt:
wobei c ein beliebiger Skalar und
| c c |
sein Absolutbetrag (als Zahl) ist. Ist
c ¹ 0,
gilt daher auch
| |
sein Absolutbetrag (als Zahl) ist. Ist
c ¹ 0,
gilt daher auch
| a/c a/c | =
| | =
| a a |/| |/| c c |. |.
Achtung: Im Allgemeinen ist
| a + b a + b | ¹
| | ¹
| a a | +
| | +
| b b |.
Es gilt aber immer die so genannte Dreiecksungleichung |.
Es gilt aber immer die so genannte Dreiecksungleichung
Angesichts der geometrischen Bedeutung der Vektoraddition (s.o.) besagt sie, dass
der direkte Weg nicht länger sein
kann als ein Umweg.
Als unmittelbare Konsequenz der Definition des Betrags
können wir den Abstand zweier Punkte durch Vektoren ausdrücken:
Sind P und Q
zwei beliebige Punkte, so ist ihr Abstand durch den Betrag des Verbindungsvektors gegeben:
Abstand zwischen
P und Q
= | P - Q P - Q | |
|
. |
|
(29) |
In Anwendungen möchte man oft die Beträge von Vektoren manipulieren. So kann ein Vektor-Pfeil in einer
Skizze für irgend einen Zweck recht brauchbar erscheinen, aber nicht die benötigte Länge
haben. Wenden wir uns also zuletzt einigen Techniken zu, die sich den Begriff des Betrags zunutze machen.
Einheitsvektoren und Normierung
| | | |
| |
| | |
Definition: Wir nennen a einen
Einheitsvektor, wenn sein Betrag gleich 1 ist, d.h. wenn
| a a |
= 1
ist. Einheitsvektoren werden manchmal auch als normiert bezeichnet. |
= 1
ist. Einheitsvektoren werden manchmal auch als normiert bezeichnet.
Ist a ein beliebiger (von 0 verschiedener) Vektor, so ist
jener Vektor, der in dieselbe Richtung wie a
zeigt, aber ein Einheitsvektor ist, durch
a
| a a | | |
|
|
(30) |
gegeben. (Beweis: Gemäß Rechengesetz (27) ist
| a/| a/| a a | | |
= | |
= | a a |/| |/| a a |
= 1.
Weiters ist der Vektor (30) ein Vielfaches von a und daher zu diesem
parallel. Da er aus a durch Multiplikation mit der
positiven Zahl | |
= 1.
Weiters ist der Vektor (30) ein Vielfaches von a und daher zu diesem
parallel. Da er aus a durch Multiplikation mit der
positiven Zahl | a a |-1 hervorgeht,
zeigt er in dieselbe Richtung).
Den Übergang von a zu
a/| |-1 hervorgeht,
zeigt er in dieselbe Richtung).
Den Übergang von a zu
a/| a a |
nennen wir Normierung, und wir sagen, dass wir
"den Vektor a normieren". |
nennen wir Normierung, und wir sagen, dass wir
"den Vektor a normieren".
Mit der Möglichkeit der Normierung von Vektoren sind einige nützliche Techniken verbunden.
Sind beispielsweise a und b
zwei (von 0 verschiedene) Vektoren, so
können wir
berechnen. Dieser Vektor zeigt genau in die Richtung der von a und b
definierten Winkelsymmetrale (Winkelhalbierende). Sehen Sie sich das anhand dieser Skizze
genauer an: a (blau) und
b (grün)
haben unterschiedliche Beträge. Die aus ihnen durch Normierung gewonnenen Einheitsvektoren
(rot)
haben aber beide den Betrag 1.
Sie definieren ein gleichseitiges Parallelogramm (eine Raute), deren Diagonale
(aus Gründen der Symmetrie) den Winkel zwischen
a und b
halbiert, und in deren Richtung die Summe (30) zeigt.
Natürlich zeigt auch jedes (nichttriviale) Vielfache von (30)
in dieselbe Richtung.
Aufgabe: Man bestimme die Richtung der Winkelsymmetrale von
a = (1, 2) und
b = (3, 4).
Lösung: Wir berechnen
| a a | = (12 + 22)1/2 = 51/2 und
| | = (12 + 22)1/2 = 51/2 und
| b b | = (32 + 42)1/2 = 251/2 = 5.
Gemäß (30) ist die Richtung der Winkelsymmetrale durch den Vektor
a/| | = (32 + 42)1/2 = 251/2 = 5.
Gemäß (30) ist die Richtung der Winkelsymmetrale durch den Vektor
a/| a a |
+ b/| |
+ b/| b b | =
(1, 2)/51/2 + (3, 4)/5 =
(5-1/2 + 3/5, 2 × 5-1/2 + 4/5)
gegeben. Wir könen dieses Resultat ein bisschen vereinfachen, z.B. das
5-fache bilden (das ja in dieselbe Richtung zeigt) und
erhalten den Vektor (3 + Ö5, 4 + 2Ö5). | =
(1, 2)/51/2 + (3, 4)/5 =
(5-1/2 + 3/5, 2 × 5-1/2 + 4/5)
gegeben. Wir könen dieses Resultat ein bisschen vereinfachen, z.B. das
5-fache bilden (das ja in dieselbe Richtung zeigt) und
erhalten den Vektor (3 + Ö5, 4 + 2Ö5).
Überprüfen Sie das Ergebnis (so genau es geht) anhand einer Zeichnung!
Manchmal ist es nützlich, einen Vektor a
¹ 0 durch einen anderen Vektor zu ersetzen, der in dieselbe
Richtung zeigt, aber den vorgegebenen Betrag c
hat. Diese Vektor ist durch
| c |
a
| a a | | |
|
|
(32) |
gegeben, kann also leicht berechnet werden. Üben wir das ein bisschen:
Aufgabe:
 Von einem Trapez (d.h. einem Viereck, in dem zwei Seiten zueinander parallel sind)
sind, gemäß der nebenstehenden Skizze, die Punkte
A,
B,
C
und die Seitenlänge
c gegeben. Gesucht ist der Punkt
D. Man löse das Problem allgemein (d.h. durch eine Formel).
Von einem Trapez (d.h. einem Viereck, in dem zwei Seiten zueinander parallel sind)
sind, gemäß der nebenstehenden Skizze, die Punkte
A,
B,
C
und die Seitenlänge
c gegeben. Gesucht ist der Punkt
D. Man löse das Problem allgemein (d.h. durch eine Formel).
Lösung: Die Seiten AB und
CD sollen zueinander parallel sein.
Der Vektor von C nach D
ist also parallel zu jenem von B nach
A, zeigt auch in dieselbe Richtung, hat aber
(möglicherweise) nicht den gleichen Betrag. Wir können ihn aber normieren und den so erhaltenen
Einheitsvektor mit c multiplizieren
- daraus ergibt sich dann der Verbindungsvektor von
C nach D.
Klicken Sie hier, um zwei für die Berechnung relevante Vektoren anzuzeigen.
Führen Sie die Details der Argumentation selbst durch!
Die Lösung ist:
D = C +
c (A - B)/| (A - B)/| A - B A - B |. |.
| | | |
| |
| | |
Mit diesen Techniken beschließen wir vorläufig unsere Vorstellung der Vektoren als wirkungsvolle mathematische Werkzeuge.
Wir werden sie in einem späteren Kapitel weiterführen.
Als ergänzende Literatur empfehlen wir das Vorlesungsskriptum
Vektorrechnung (PDF-Datei, von M. A. Knus, ETH Zürich).
|
| | |

Vektoren 2
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Im zweiten Vektorkapitel werden wir zwei weitere Rechenoperationen für Vektoren
kennen lernen:
- Das so genannte Skalarprodukt, das es erlaubt, Winkelbeziehungen zwischen Vektoren
zu analysieren und auf bequeme Weise zu entscheiden, ob zwei Vektoren aufeinander normal stehen.
- Das so genannte Vektorprodukt für räumliche Vektoren, das
mit dem Volumsinhalt und mit den Begriffen "links" und "rechts" zusammenhängt.
| | | |

Vektoren 2
| |
| | |
Dafür ist es günstig, ein bisschen über Winkelfunktionen
zu wissen. Falls Sie darüber noch nichts gehört haben, aber dennoch zum zweiten Vektorkapitel übergehen wollen,
so ist das für den Großteil des Kapitels nicht allzu schlimm. Es wird Ihnen dort an einer entscheidenden Stelle
eine "Umfahrung" angeboten.
| | | |

Winkelfunktionen
| |
| | |
Danach werden wir noch zweimal auf die Theorie der Vektoren zurückkommen:
- Im Kapitel über mathematische Strukturen und Räume, das
erklärt, wieso die Mathematik unentwegt
an der Formalisierung und Verallgemeinerung des bisher Erreichten interessiert ist,
- und in einem Kapitel über die lineare Algebra, dem Gebiete der Mathematik,
das der allgemeinen Theorie der "Vektorräume" und der sie beherbergenden
Strukturen gewidmet ist. Im Rahmen dieser Theorie bekommt der Begriff
linear, der in vielen Zusammenhängen verwendet wird, eine sehr
allgemeine Bedeutung.
| | | |

mathematische Strukturen
(in Vorbereitung)

lineare Algebra
(in Vorbereitung)
| |
| | |
Die moderne Mathematik kennt auch etliche Verallgemeinerungen des Vektorbegriffs.
- Matrizen sind "rechteckige" Zahlenanordnungen (verallgemeinern in diesem Sinn den Begriff des
Vektors als "Liste von Zahlen") und sind unter anderem beim Lösen von
Gleichungssystemen behilflich.
- Geometrische Objekte, die mit Vektoren verwandt sind und in der Physik (z.B. in der
Relativitätstheorie) eine wichtige Rolle spielen, sind die Tensoren.
- Schließlich werden in einem späteren Kapitel "Vektorfelder", die insbesondere für die moderne
Physik wichtig sind, besprochen.
| | | |

Matrizen
(in Vorbereitung)

Tensoren
(in Vorbereitung)

Vektorfelder
(in Vorbereitung)
| |
| | |
Die Vektorrechnung findet in zahlreichen Gebieten der Mathematik Anwendung. Wir erwähnen hier
lediglich einige Kapitel, in denen Sie Vektoren als Hilfmittel begegnen werden:
- Insgesamt drei Kapiteln sind der analytischen Geometrie gewidmet. Die Bezeichnung "analytisch"
bezieht sich darauf, dass geometrische Probleme durch das Mittel der Berechnung
analysiert und gelöst werden. Genau dabei stellen Vektoren eine
unschätzbare Hilfe dar.
- Vektoren helfen bei der Frage, welche Lösungen Gleichungssysteme haben können,
und beim praktischen Auffinden dieser Lösungen.
- Die komplexen Zahlen (ein formales Zahlensystem, innerhalb dessen es möglich ist, die Wurzeln aus
negativen Zahlen zu ziehen) können als zweikomponentige Vektoren dargestellt werden.
- Zahlreiche anspruchsvolle Gebiete der höheren Mathematik, wie etwa jenes der Differentialgleichungen,
greifen auf sie zurück.
|
| | |

Analytische Geometrie 1

Gleichungssysteme

komplexe Zahlen
(in Vorbereitung)

Differentialgleichungen
(in Vorbereitung)
| |