| | |
| | | |
| |
| | |
| Matrizen und lineare Abhängigkeiten |
| | | |
| |
| | |
Was sind Matrizen...
Nicht-Eingeweihten gelten Matrizen manchmal als mysteriöse Objekte, die das Leben erschweren, weil sie es mit noch mehr Mathematik
anreichern. In Wahrheit sind sie aber erfunden worden, um das (mathematische) Leben zu erleichtern!
Zunächst ist eine Matrix einfach ein "rechteckiges Zahlenschema". Ein Beispiel einer Matrix ist
|
$M=\left(\begin{array}{cc}
1 & -2\\
4 & 0\\
3 & 5
\end{array}\right)
$
|
. |
|
$(1)$ |
| | | |
| |
| | |
Das gesamte Schema bezeichnen wir mit einem einzigen Buchstaben, in diesem Fall $M$, ganz so, wie wir es bei Vektoren machen.
Die jeweils nebeneinander stehenden Zahlen bilden eine Zeile der Matrix, die jeweils untereinander stehenden Zahlen bilden
eine Spalte. Die Matrix (1) besitzt $3$ Zeilen und $2$ Spalten. Wir bezeichnen sie als eine
$3\times 2$-Matrix (ausgesprochen "3 mal 2-Matrix"), um ihre "Größe" (genauer: ihre Dimension) anzugeben. Die
Zahlen, die eine Matrix bilden, nennen wir ihre Komponenten. Bei Bedarf kann die Komponente, die in der $j$-ten Zeile und in der
$k$-ten Spalte steht, mit $M_{jk}$ bezeichnet werden. Für die Matrix (1) ist daher etwa $M_{11}=1$ und $M_{32}=5$.
Ganz allgemein besitzt eine $m\times n$-Matrix $m$ Zeilen und $n$ Spalten. $m$ und $n$ stehen sozusagen für die "Höhe" und die
"Breite" des Zahlenschemas. Eine Matrix, die gleich viele Zeilen wie Spalten besitzt, nennen wir quadratisch (da sie ein quadratisches
Zahlenschema darstellt). Ein Beispiel für eine $2\times 2$-Matrix ist
|
$Q=\left(\begin{array}{cc}
1 & -2\\
3 & 4
\end{array}\right)
$
|
. |
|
$(2)$ |
Vektoren sind Spezialfälle von Matrizen, wobei wir zwei Möglichkeiten haben, sie anzuschreiben. Hier zwei Beispiele:
|
$u=\left(\begin{array}{c}
1\\
3
\end{array}\right)
{\sf,}\qquad
v=\left(\begin{array}{cc}
1 & 3
\end{array}\right)
$
|
. |
|
$(3)$ |
$u$ ist ein sogenannter Spaltenvektor (in diesem Fall eine $2\times 1$-Matrix), $v$ ein Zeilenvektor
(in diesem Fall eine $1\times 2$-Matrix). Eine einzige alleinstehende Zahl kann – mit ein bisschen
Haarspalterei – auch als $1\times 1$-Matrix angesehen werden.
Wozu betrachten wir derartige Objekte? Schon die Idee des "Zahlenschemas" deutet darauf hin, dass die betreffenen Zahlen
irgendeine Bedeutung haben, und dass ihre Zusammenfassung in einer Matrix vor allem der Bequemlichkeit dient.
Da Matrizen ausgerechnet in einem Mathematik-Kapitel auftreten, lässt vermuten, dass man mit ihnen rechnen kann.
Beide Aspekte werden im Folgenden eine wichtige Rolle spielen.
| | | |

Vektoren 1
| |
| | |
...und wozu dienen sie?
Matrizen erleichtern das Leben, wenn es um lineare Zusammenhänge zwischen mehreren Größen geht.
Machen wir das gleich anhand eines Beispiels deutlich: Angenommen, in irgendeiner konkreten Situation
treten vier Größen $x_1$, $x_2$, $y_1$ und $y_2$ auf.
Nun stellen wir uns vor, dass $y_1$ und $y_2$ in einer ganz bestimmten Weise von $x_1$ und $x_2$
abhängen, nämlich
|
\begin{eqnarray}
y_1 &=& 7x_1 + 3x_2\\
y_2 &=& 2x_1 + 8x_2
\end{eqnarray}
|
. |
|
$(4)$ |
Derartige Abhängigkeiten treten in der Praxis oft auf.
Beispiel: Stellen wir uns ein Unternehmen vor, das zwei Arten von Duftstoffen für Wohnräume
auf den Markt bringt ("Frühling" und "Exotic"), indem zwei Rohstoffe, die die Firma einkauft (Veilchenduft und Jasminöl)
in unterschiedlichen Zusammensetzungen gemischt werden:
- 10 kg des Duftes "Frühling" bestehen aus $7$ kg Veilchenduft und $3$ kg Jasminöl.
- 10 kg des Duftes "Exotic" bestehen aus $2$ kg Veilchenduft und $8$ kg Jasminöl.
Die Kosten für Veilchenduft und Jasminöl steigen von Zeit zu Zeit ein bisschen.
Wir legen uns daher nicht auf konkrete Werte fest, sondern bezeichnen
- den Preis (in Euro) für 1 kg Veilchenduft mit $x_1$
- und den Preis (in Euro) für 1 kg Jasminöl mit $x_2$.
Das Unternehmen interessiert sich nun für zwei Dinge:
- Wieviel muss es (in Euro) für die Rohstoffe zahlen, die für 10 kg "Frühling" benötigt werden?
Antwort: $y_1$, wie in (4) angegeben.
- Wieviel muss es (in Euro) für die Rohstoffe zahlen, die für 10 kg "Exotic" benötigt werden?
Antwort: $y_2$, wie in (4) angegeben.
Und hier haben wir eine Abhängigkeit zweier Größen ($y_1$ und $y_2$) von zwei anderen Größen
($x_1$ und $x_2$) in einem praktischen Beispiel, wie sie in mathematischer Symbolschreibweise durch (4) ausgedrückt wird!
Wir werden uns im Folgenden noch einige Male (in eingerückten dunkelblauen Texten) auf dieses Beispiel beziehen.
Betrachten wir die mathematische Struktur von (4) genauer:
Wann immer konkrete Zahlen für $x_1$ und $x_2$ angegeben werden, sind $y_1$ und $y_2$ durch die
Beziehungen (4) eindeutig bestimmt. Sowohl $y_1$ als auch $y_2$ ist von der Form
|
gegebene Zahl mal $x_1$ $+$ gegebene Zahl mal $x_2$
|
. |
|
$(5)$ |
Eine solche Form der Abhängigkeit bezeichnen wir als linear-homogen (manchmal einfach nur als "linear").
Die beiden "gegebenen Zahlen", die hier auftreten, heißen Koeffizienten, ein Ausdruck der Form
(5) heißt Linearkombination von $x_1$ und $x_2$.
In den Beziehungen (4)
treten vier Koeffizienten auf, zwei für $y_1$ und zwei für $y_2$, die wir übersichtlich in Form eines
"quadratischen Zahlenschemas", also als $2\times 2$-Matrix
|
$A=\left(\begin{array}{cc}
7 & 3\\
2 & 8
\end{array}\right)$
|
|
|
$(6)$ |
zusammenfassen können. Sie stehen an den gleichen Positionen wie in (4), wobei alle anderen Symbole weggelassen und nur die Klammern
(die uns anzeigen, dass es sich um eine Matrix handelt) hinzugefügt werden. Hier haben wir eine erste Matrix, die eine konkrete
Aufgabe erfüllt: Sie fasst die konkrete, durch (4) definierte lineare Abhängigkeit in knapper Form zusammen.
(Wenn wir in diesem Abschnitt "linear" sagen, meinen wir damit immer "linear-homogen").
Nun könnte man einwenden, dass ein Objekt wie (6) zwar ein bisschen Schreibarbeit erspart, dass aber die Aussage,
die (4) macht, nicht mehr ersichtlich ist. Das ist ein guter Einwand, und wir berücksichtigen ihn, indem
wir die vier Größen $x_1$, $x_2$, $y_1$ und $y_2$, die ebenfalls in (4) vorkommen,
in Form zweier Spaltenvektoren zusammenfassen:
|
$x=\left(\begin{array}{c}x_1\\x_2\end{array}\right)
{\sf,}\qquad
y=\left(\begin{array}{c}y_1\\y_2\end{array}\right)$
|
. |
|
$(7)$ |
Damit haben wir alle in (4) auftretenden Größen systematisch zusammengefasst:
- Die beiden (unabhängigen) Variablen $x_1$ und $x_2$ im Spaltenvektor $x$,
- Die beiden (abhängigen) Variablen $y_1$ und $y_2$ im Spaltenvektor $y$
- und die angegebenen Koeffizienten in der Matrix $A$.
Und jetzt "erfinden" wir eine Rechenoperation, die es erlaubt, eine Matrix mit einem Vektor zu
"multiplizieren".
| | | |
| |
| | |
Matrix mal Vektor
(4) besteht aus zwei Aussagen, die die Werte von $y_1$ und $y_2$ in Abhängigkeit der Werte von $x_1$ und $x_2$ festlegen.
Schaffen wir es, diese beiden Aussagen in einer einzigen (vereinheitlichten) Form "$y=\dots$" anzuschreiben?
Eine Vorschrift, die angibt, wie der Spaltenvektor $y$ berechnet werden kann, besteht ja im Grunde nur aus zwei Vorschriften,
einer für $y_1$ und einer für $y_2$. Dazu wagen wir die Idee, dass es möglich sein könnte, die
Matrix $A$ so mit dem Vektor $x$ zu "multiplizieren", dass das Ergebnis $y$ ist!
Das ist gar nicht so schwer. Wenn wir diese "Multiplikation" in der Form "$Ax$" anschreiben, müsste also gelten:
|
$\left(\begin{array}{cc}
7 & 3\\
2 & 8
\end{array}\right) \left(\begin{array}{c}x_1\\x_2\end{array}\right) =
\left(\begin{array}{cc}7x_1+3x_2\\2x_1+8x_2\end{array}\right)$
|
. |
|
$(8)$ |
Erkennen Sie die Regel, wie hier vorgegangen werden muss?
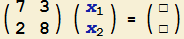
1. Wie lautet die Regel, um das
gewünschte Ergebnis zu erhalten? |
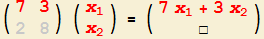
2. So erhalten Sie die erste Komponente
des Ergebnisses! |
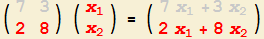
3. So erhalten Sie die zweite Komponente
des Ergebnisses! |
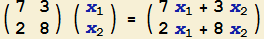
4. Das ist das Ergebnis! |
Gehen Sie so vor:
- Um die erste Komponente des Ergebnis-Vektors zu erhalten (oben, 2), schauen Sie auf die erste Zeile der Matrix und auf die (einzige) Spalte des Vektors.
Bilden Sie "erste Zahl dieser Zeile mal erste Zahl der Spalte + zweite Zahl dieser Zeile mal zweite Zahl der Spalte".
- Um die zweite Komponente des Ergebnis-Vektors zu erhalten (oben, 3), schauen Sie auf die zweite Zeile der Matrix und auf die (einzige) Spalte des Vektors.
Bilden Sie "erste Zahl dieser Zeile mal erste Zahl der Spalte + zweite Zahl dieser Zeile mal zweite Zahl der Spalte".
| | | |
| |
| | |
Mit Hilfe des Skalarprodukts von Vektoren können wir diese Regel auch so formulieren:
- Um die erste Komponente des Ergebnis-Vektors zu erhalten (oben, 2), bilden Sie das Skalarprodukt der ersten Zeile der Matrix mit der (einzige) Spalte des Vektors.
- Um die zweite Komponente des Ergebnis-Vektors zu erhalten (oben, 3), bilden Sie das Skalarprodukt der zweiten Zeile der Matrix mit der (einzigen) Spalte des Vektors.
Auf dem Papier wenden Sie diese Regel am besten unter Zuhilfehahme ihrer beiden Hände an:
- Um die erste Komponente des Ergebnis-Vektors zu erhalten (oben, 2),
legen Sie zuerst den linken Zeigefinger auf die erste Zahl in der ersten Zeile der Matrix
und den rechten Zeigefinger auf die erste Komponente des Vektors. Diese beiden Zahlen werden miteinander multipliziert.
Nun bewegen Sie den linken Zeigefinger nach rechts und gleichzeitig den rechten Zeigefinger nach unten.
Alle Zahlen, auf denen ihre Zeigefinger gleichzeitig stehen, werden miteinander multipliziert, und alle diese Produkte.werden addiert
- Um die zweite Komponente des Ergebnis-Vektors zu erhalten (oben, 3), legen Sie zuerst den linken Zeigefinger auf die erste Zahl in der zweiten Zeile der Matrix
und den rechten Zeigefinger auf die erste Komponente des Vektors. Dann wiederholen Sie den Vorgang, wobei ihr linker Zeigefinger nun die zweite Zeile
der Matrix überstreicht.
Auf diese Weise überstreicht ihr linker Zeigefinger immer eine Zeile der Matrix und gleichzeitig der rechte den Vektor.
Verstanden?
Hier ein Beispiel, in dem nur Zahlen vorkommen:
$$\left(\begin{array}{cc}
-1 & 3\\
4 & 2
\end{array}\right) \left(\begin{array}{c}6\\5\end{array}\right) =
\left(\begin{array}{c}(-1)\cdot 6 + 3 \cdot 5\\4\cdot 6+2\cdot 5\end{array}\right) =
\left(\begin{array}{c}-6 + 15\\24+10\end{array}\right) =
\left(\begin{array}{c}9\\34\end{array}\right)\,{\sf\small.}$$
Üben Sie weitere derartige Multiplikationen mit selbsterfundenen Matrizen und Vektoren!
Mit dieser Art, eine $2\times 2$-Matrix mit einem $2\times 1$-Spaltenvektor zu multiplizieren, lauten die Beziehungen
(4) nun einfach
Damit haben wir die durch (4) gegebene lineare Abhängigkeit zweier Größen von
zwei anderen Größen in einer sehr knappen Form angeschrieben. Mit Hilfe von (6) und
(7) und der soeben erfundenen "Multiplikation" kann daraus die ursprügliche Form (4)
zurückgewonnen werden. Die Kurzform (9) besitzt daher den gleichen Informationsgehalt wie (4).
Beispiel: Unser oben beschriebenes Unternehmen, das Duftstoffe verkauft, kann nun
mit Hilfe der Matrix (6) auf übersichtliche Weise darstellen, wie die Rohstoffkosten für die
Herstellung von 10 kg "Frühling" und von 10 kg "Exotic" von den Marktpreisen für Veilchenduft ($x_1$)
und Jasminöl ($x_2$) abhängen. Die konkreten Werte, die $x_1$ und $x_2$ annehmen, ändern sich von Zeit zu Zeit, so dass
die konkreten Rohstoffkosten für die beiden Produkte dann immer mit Hilfe einer Multiplikation
"Matrix mal Spaltenvektor" ermittelt werden können.
Wenn man nun eine Matrix mit einem Vektor multiplizieren kann – ist es dann auch möglich, eine Matrix mit einer
Matrix zu multiplizieren? Und welchen Sinn sollte das haben?
| | | |

Skalarprodukt
| |
| | |
Matrix mal Matrix: die Matrizenmultiplikation
Stellen wir uns vor, die beiden Größen $x_1$ und $x_2$ hängen ihrerseits auf lineare Weise von zwei
weiteren Größen $u_1$ und $u_2$ ab, also beispielsweise
|
\begin{eqnarray}
x_1 &=& 900\,u_1 + 150\,u_2\\
x_2 &=& 500\,u_1 + 400\,u_2
\end{eqnarray}
|
. |
|
$(10)$ |
Auch so etwas kann in der Praxis vorkommen!
Beispiel: Der Verkäufer der
Rohstoffe Veilchenduft und Jasminöl, die unser Duftstoff-Unternehmen benötigt, stellt diese aus zahlreichen
importierten Grundstoffen her. Seit Beginn des Jahres 2010 sind die Kosten für den Einkauf dieser Grundstoffe generell
um den Faktor $u_1$ gestiegen und die heimischen Produktionskosten um den Faktor $u_2$, die beide auf die entsprechenden
Preisanteile aufgeschlagen werden:
- Zu Beginn des Jahres 2010 waren für 1 kg Veilchenduft der benötigten Konzentration
1050 Euro zu bezahlen, davon 900 für den Kauf der Grundstoffe und 150 für die heimische Produktion.
Zu einem späteren Zeitpunkt ist der Gesamtpreis dafür (in Euro) daher auf $\,x_1=900\,u_1+150\,u_2\,$ gestiegen.
- Zu Beginn des Jahres 2010 waren für 1 kg Jasminöl der benötigten Konzentration
900 Euro zu bezahlen, davon 500 für den Kauf der Grundstoffe und 400 für die heimische Produktion.
Zu einem späteren Zeitpunkt ist der Gesamtpreis dafür (in Euro) daher auf $\,x_2=500\,u_1+400\,u_2\,$ gestiegen.
Also wieder eine lineare Abhängigkeit zweier Größen ($x_1$ und $x_2$) von zwei anderen Größen
($u_1$ und $u_2$), wie sie durch (10) ausgedrückt wird!
Die Beziehungen (10) können wir mit einem Spaltenvektor $u$, dessen Komponenten $u_1$ und $u_2$ sind, und
mit Hilfe der Matrix
|
$B=\left(\begin{array}{cc}
900 & 150\\
500 & 400
\end{array}\right)$
|
|
|
$(11)$ |
in der Form
schreiben. Wie hängen nun $y_1$ und $y_2$ von $u_1$ und $u_2$ ab?
Beispiel: Für unser Duftstoff-Unternehmen bedeutet diese Frage:
Wie hängen die Rohstoffkosten für die Herstellung von 10 kg "Frühling" und von 10 kg "Exotic"
von den Teuerungsraten $u_1$ der Grundstoffpreise und $u_2$ der heimischen Produktion ab?
Wenn wir (10) in (4) einsetzen, erhalten wir
|
\begin{eqnarray}
y_1 &=& 7(900\,u_1 + 150\,u_2) + 3(500\,u_1 + 400\,u_2) &=& 7800\,u_1 + 2250\,u_2\\
y_2 &=& 2(900\,u_1 + 150\,u_2) + 8(500\,u_1 + 400\,u_2) &=& 5800\,u_1 + 3500\,u_2
\end{eqnarray}
|
. |
|
$(13)$ |
Das ist also wieder eine lineare Abhängigkeit, die mit Hilfe der Matrix
|
$C=\left(\begin{array}{cc}
7800 & 2250\\
5800 & 3500
\end{array}\right)$
|
|
|
$(14)$ |
in der knappen Form
ausgedrückt werden kann. Die Matrix $C$ stellt die "ineinandergeschachtelten" linearen Abhängigkeiten dar, die durch die Matrizen
$A$ und $B$ dargestellt worden sind. Sie ist also durch $A$ und $B$ eindeutig bestimmt.
Kann sie durch eine Art "Multiplikation" aus $A$ und $B$ gewonnen werden?
Die Antwort ist ja: Wenn wir (12) in (9) einsetzen, ergibt sich
Durch den Vergleich dieser Form des "Hintereinander-Ausführens" zweier Multiplikationen
(zuerst $B$ mit $u$ und danach $A$ mit dem Ergebnis $Bu$) mit (15) ergibt sich
$Cu=A(Bu)$. Nun definieren wir einfach das Produkt der Matrizen $A$ und $B$
als die Matrix $C$ und schreiben es als $AB$ an. Damit nimmt (16) die Form
$y=(AB)u$ an, was üblicherweise ohne Klammern in der Form
angeschrieben wird. Gehen Sie das Argument, das zu dieser Definition geführt hat, noch einmal durch!
Der Grundgedanke ist einfach:
- Eine Matrix stellt eine lineare Abhängigkeit dar.
- Das Produkt zweier Matrizen stellt zwei ineinandergeschachtelte lineare Abhängigkeiten
(die ja in Kombination wieder eine lineare Abhängigkeit ergeben) dar!
Dieses Ineinanderschachteln legt die eindeutige Rechenvorschrift der Matrizenmultiplikation fest,
zunächst für $2\times 2$-Matrizen. Die Regel ist ähnlich wie jene für das
Produkt einer Matrix mit einem Spaltenvektor. Wir wünschen uns also
|
$\left(\begin{array}{cc}
7 & 3\\
2 & 8
\end{array}\right) \left(\begin{array}{cc}
900 & 150\\
500 & 400
\end{array}\right) = \left(\begin{array}{cc}
7800 & 2250\\
5800 & 3500
\end{array}\right)$
|
. |
|
$(18)$ |
Um die allgemeine Regel zu entdecken, sehen Sie sich an, wie die Zahlen, die jeweils zwischen den beiden Gleichheitszeichen in (13)
stehen, miteinander kombiniert werden müssen!
Hier ein Schema in vier Stationen, wie Sie die vier Komponenten der Ergebnis-Matrix erhalten:

1. So erhalten Sie die Komponente
mit Zeilennummer 1 und Spaltennummer 1
der Ergebnis-Matrix! |
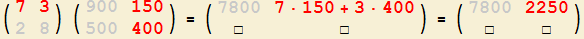
2. So erhalten Sie die Komponente
mit Zeilennummer 1 und Spaltennummer 2
der Ergebnis-Matrix! |
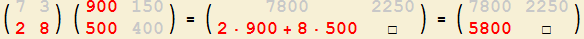
3. So erhalten Sie die Komponente
mit Zeilennummer 2 und Spaltennummer 1
der Ergebnis-Matrix! |
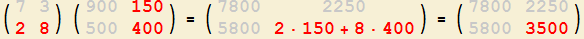
4. So erhalten Sie die Komponente
mit Zeilennummer 2 und Spaltennummer 2
der Ergebnis-Matrix! |
Am besten lassen Sie dazu den linken Zeigefinger immer eine Zeile der ersten Matrix überstreichen und
gleichzeitig den rechten über eine Spalte der zweiten Matrix, und dabei bilden Sie die Produkte der Zahlen, über denen Ihre
Zeigefinger jeweils stehen und addieren sie.
Dabei wählen Sie die Zeile der ersten und die Spalte der zweiten Matrix entsprechend der Position
der Komponenten der Ergebnis-Matrix, die Sie gerade berechnen.
Durch das Skalarprodukt ausgedrückt lautet die Regel:
|
Regel für die Matrizenmultiplikation:
Um die Komponente mit Zeilennummer $j$ und Spaltennummer $k$ der Ergebnis-Matrix
zu erhalten, bilden Sie das Skalarprodukt der $j$-ten Zeile der ersten Matrix mit der $k$-ten Spalte der zweiten Matrix.
|
Damit ist also nichts anderes ausgeführt als die in (13)
durchgeführte Berechnung der Abhängigkeit, die sich aus dem Ineinanderschachteln zweier
vorher festgelegter lihnearer Abhängigkeiten ergibt.
Beispiel: Unser Duftstoff-Unternehmen kann nun aus den Informationen, die in den
Matrizen $A$ (Kosten für die beiden hergestellten Produkte in Abhängigkeit von den Rohstoffpreisen)
und $B$ (Rohstoffpreise in Abhängigkeit von den Teuerungsraten am Grundstoffsektor und in der heimischen Produktion)
durch die Matrizenmultiplikation $C=AB$ mit einem Schlag die Kosten in Abhängigkeit von den Teuerungsraten berechnen.
Sind die Teuerungsraten $u$ für einen bestimmten Zeitpunkt bekannt, so werden die anfallenden Kosten
dann einfach in der Form $y=Cu$ ermittelt. Das Unternehmen lässt diese Berechnungen natürlich von einem Computer
ausführen, der das dafür nötige Jonglieren mit Zahlen perfekt beherrscht.
Die durch die obige Vorschrift definierte Matrizenmultiplikation wird "Multiplikation" genannt, weil sie
ein bisschen an die Multiplikation von Zahlen erinnert und man in mancher Hinsicht mit ihr so rechnen kann.
Dennoch handelt es sich bei ihr um ein anderes mathematisches Konzept, das bestimmten
Überlegungen entsprungen ist und bestimmten Zwecken dient (z.B., wie wir gesehen haben, der Beschreibung
ineinandergeschachtelter linearer Abhängigkeiten). Es sollte daher nicht mit der
Multiplikation von Zahlen verwecnselt werden.
Eine wichtige Eigenschaft, die den Unterschied verdeutlich, besteht darin, dass die Matrizenmultiplikation von der Reihenfolghe der Faktoren
abhägt: $AB$ ist im Allgemeinen von $BA$ verschieden! Man sagt auch, dass die Matrizenmultiplikation "nicht kommutativ"
ist. Probieren Sie es aus, indem Sie mit den beiden oben betrachteten Matrizen $BA$ berechnen und mit $AB$
vergleichen! (Danach klicken Sie auf den nebenstehenden Button, um ihr Ergebnis zu überprüfen!)
| | | |
| |
| | |
Allgemeine Matrizenmultiplikation
Können wir nun beliebige Matrizen nach dem obigen Schema miteinander multiplizieren? Nein! Ob wir zwei
Matrizen miteinander multiplizieren können, hängt von ihrer Dimension ab, d.h. davon, wie viele
Zahlen und Spalten sie besitzen. Wenn Sie die obige Regel für die Matrizenmultiplikation bedenken, muss die Länge einer Zeile der ersten Matrix
gleich der Länge einer Spalte der zweiten Matrix sein. In anderen Worten: Die erste Matrix muss genausoviele Spalten
besitzen wie die zweite Matrix Zeilen. Daher gilt:
|
Das Produkt $AB$ zweier Matrizen kann nur gebildet werden, wenn $A$ eine $m\times n$-Matrix und $B$ eine $n\times p$ Matrix ist.
|
Das Produkt der beiden Matrizen hat dann nach unserer Regel genau so viele Zeilen wie die erste Matrix und genau so viele Spalten
wie die zweite Matrix. Das Produkt $AB$ einer $m\times n$-Matrix $A$ mit einer $n\times p$-Matrix $B$ ist daher
eine $m\times p$-Matrix. Schematisch sieht das so aus:
|
$(m\times n$-Matrix$)\,(n\times p$-Matrix$)=(m\times p$-Matrix$)$.
|
Dazu ein Beispiel:
$$\left(\begin{array}{cc}
-1 & 3\\
4 & 2\\
7 & 8
\end{array}\right)
\left(\begin{array}{cc}
6 & -2\\
5 & 9
\end{array}\right) =
\left(\begin{array}{cc}
(-1)\cdot 6 + 3\cdot 5 & (-1)\cdot(-2)+3\cdot 9\\
4\cdot 6 + 2\cdot 5 & 4\cdot(-2)+2\cdot 9\\
7\cdot 6 + 8\cdot 5 & 7\cdot(-2)+8\cdot 9
\end{array}\right) =
\left(\begin{array}{cc}
9 & 29\\
34 & 10\\
82 & 58
\end{array}\right)$$
Hier wird eine $3\times 2$-Matrix mit einer $2\times 2$-Matrix multipliziert. Das Ergebnis ist eine $3\times 2$-Matrix.
Beispiel: Wenn unser Duftstoff-Unternehmen seine Produktion ausweitet und $m$ Produkte herstellt,
die aus $n$ Rohstoffen zusammengesetzt werden, wird die Abhängigkeit der Rohstoffkosten für die $m$ Produkte von den
Preisen der $n$ Rohstoffe durch eine $m\times n$-Matrix $A$ beschrieben. Wenn die Preise dieser $n$ Rohstoffe
von $p$ Teuerungsraten in verschiedenen Wirtschaftssektoren (in linearer Weise) abhängen, so wird diese
Abhängigkeit durch eine $n\times p$-Matrix $B$ beschrieben. Die Abhängigkeit der Rohstoffkosten von den
Teuerungsraten wird dann durch das Produkt $C=AB$ beschrieben, was eine $m\times p$-Matrix ist:
Die Rohstoffkosten für $m$ Produkte hängen von $p$ Teuerungsraten ab.
In dem einfachen Beispiel, das bisher betrachtet wurde, war $m=n=p=2$ gesetzt.
Mit der Regel für die Matrizenmultiplikation erweist sich die oben zuerst eingeführte
Multiplikation einer $2\times 2$-Matrix mit einem zweidimensionalen Spaltenvektor als einfacher Spezialfall:
$(2\times 2$-Matrix$)\,(2\times 1$-Matrix$)=(2\times 1$-Matrix$)$.
Das Produkt zweier quadratischer Matrizen der gleichen Dimension ergibt wieder eine ebensolche Matrix.
Daher können wir mit quadratischen Matrizen Potenzen wie $A^2=AA$ und $A^3=AAA$ bilden.
| | | |
| |
| | |
Assoziativität
Eine nützliche Eigenschaft der Matrizenmultiplikation besteht darin, dass sie ist assoziativ ist:
Wenn wir von drei Matrizen $A$, $B$ und $C$ ausgehen, die von ihren Dimensionen gestatten, zuerst $AB$ und danach
$(AB)C$ zu berechnen, so erhalten wir das gleiche Resultat, wenn zuerst $BC$ und danach $A(BC)$ berechnet wird.
Wir können in einem solchen Fall daher die Klammern weglassen und einfach $ABC$ schreiben:
|
$(AB)C=A(BC)\equiv ABC$
|
. |
|
$(19)$ |
Das ist der Grund, warum wir in (17) keine Klammern geschrieben haben. So gesehen entsteht
(17) aus (16), indem einfach die Klammern weggelassen werden.
| | | |
| |
| | |
Vielfache und Summen von Matrizen
Zusätzlich zur Matrizenmultiplikation drängen sich zwei weitere Operationen mit Matrizen förmlich auf:
Ein Vielfaches einer beliebigen Matrix wird gebildet, indem alle Komponenten mit der gleichen Zahl multipliziert werden.
Hier ein Beispiel:
|
$3\left(\begin{array}{cc}
7 & -2\\
4 & 0\\
5 & 1
\end{array}\right)
=\left(\begin{array}{cc}
3\cdot 7 & 3\cdot (-2)\\
3\cdot 4 & 3\cdot 0\\
3\cdot 5 & 3\cdot 1
\end{array}\right)=
\left(\begin{array}{cc}
21 & -6\\
12 & 0\\
15 & 3
\end{array}\right)
$
|
. |
|
$(20)$ |
Matrizen gleicher Dimension können addiert werden, indem die Koeffizienten, die der gleichen Position
(also der gleichen Zeilen- und Spaltennummer) entsprechen, addiert werden.
Hier ein Beispiel:
|
$\left(\begin{array}{cc}
7 & -2\\
4 & 0\\
-5 & 3
\end{array}\right)
+\left(\begin{array}{cc}
2 & 5\\
-3 & 4\\
1 & 2
\end{array}\right)=
\left(\begin{array}{cc}
7+2 & -2+5\\
4-3 & 0+4\\
-5+1 & 3+2
\end{array}\right)=
\left(\begin{array}{cc}
9 & 3\\
1 & 4\\
-4 & 5
\end{array}\right)
$
|
. |
|
$(21)$ |
Die Addition von Matrizen und das Bilden von Vielfachen schließen das Bilden von Differenzen mit ein, da
$A-B$ als $A+(-1)B$ interpretiert werden kann. Allgemeiner können mit Matrizen gleicher Dimension beliebige Linearkombinationen
(wie beispielsweise $3A-5B+6C$ für drei Matrizen $A$, $B$; und $C$) gebildet werden.
Hinsichtlich des Bildens von Vielfachen und der Addition kann also mit Matrizen genauso gerechnet werden wie
mit Vektoren. (Die Spezialisten sagen, dass die Menge aller Matrizen der gleichen Dimension einen Vektorraum
bilden).
| | | |

(in Vorbereitung)
Vektorraum
| |
| | |
Distributivität
Die bisher definierten Operationen für Matrizen spielen insofern sehr schön zusammen,
als sich das Rechnen mit Klammern genauso gestaltet wie beim Umgang mit Zahlen (wobei lediglich darauf geachtet werden muss, dass
die Reihenfolge von Matrizen, die multipliziert werden, nicht vertauscht werden darf). Insbesondere gilt
für beliebige Matrizen $A$, $B$ und $C$ (deren Dimensionen die folgenden Operationen erlauben)
|
\begin{eqnarray}
A(B+C)&=&AB+AC\\
(A+B)\,C&=&AC+BC
\end{eqnarray}
|
. |
|
$(22)$ |
Diese Rechenregeln werden unter dem Namen Distributivitätsgesetz
zusammengefasst.
| | | |

Distributivgesetz für
reelle Zahlen
| |
| | |
Nullmatrix
In jeder Dimension $m\times n$ wird die Matrix, deren Komponenten alle gleich $0$ sind, als Nullmatrix
bezeichnet und in der Regel einfach mit dem Symbol $0$ angeschrieben.
Die Nullmatrix hat die Eigenschaft, dass sich nichts ändert, wenn sie zu einer Matrix $A$ (der gleichen Dimension)
addiert wird: $A+0=A$. Weiters gilt stets $0A=A0=0$.
| | | |
| |
| | |
Einheitsmatrix
Eine spezielle Form der linearen Abhängigkeit zweier Größen besteht darin, dass sie gleich sind:
$y_1=x_1$ und $y_2=x_2$. Dieser Abhängigkeit entspricht die so genannte Einheitsmatrix,
die wir mit $\mathbf{1}$ bezeichnen:
|
$\mathbf{1}=\left(\begin{array}{cc}
1 & 0\\
0 & 1
\end{array}\right)
$
|
. |
|
$(23)$ |
Andere in der Literatur anzutreffende Bezeichnungen sind $E$, $I$ oder ${\rm id}$.
Die Einheitsmatrix hat klarerweise die Eigenschaft, dass die Multiplikation mit einer beliebigen $2\times 2$-Matrix diese
nicht ändert:
|
$A\,\,\mathbf{1} = \mathbf{1}\,A = A
$
|
. |
|
$(24)$ |
Probieren Sie es aus, indem Sie $A\,\,\mathbf{1}$ und $\mathbf{1}\,A = A$ mit der Matrix (6) berechnen!
Ganz analog gibt es in jeder Dimension $n$ eine $n\times n$-Einheitsmatrix, bei der auf der "Hauptdiagonalen"
(von links oben nach rechts unten) $1$ steht und an allen anderen Stellen $0$, und (24) gilt ebenfalls in
jeder Dimension.
| | | |
| |
| | |
Inverse Matrix
Können wir mit Matrizen dividieren? Ja und nein – das kommt drauf an! Manchmal geht es, manchmal nicht, wie bei Zahlen!
Erinnern wir uns, was die Division für Zahlen eigentlich bedeutet und wie sie auf die Multiplikation zurückgeführt werden kann:
Ist $r\neq 0$ eine reelle Zahl, so ist ihr Kehrwert jene (eindeutig bestimmte) reelle Zahl $s$, für die $r\,s=1$ gilt.
Wir bezeichnen dann $s$ als $1/r$ oder $r^{-1}$ und können nun für zwei Zahlen $t$ und $r$ den Quotienten
$t/r$ als das Produkt $r^{-1}t$ definieren. Die Division $t/r$ ist nur möglich, wenn $r\neq 0$ ist.
Sehen wir uns nun an, ob wir das Konzept des Kehrwerts auf Matrizen übertragen können!
Wenn $y_1$ und $y_2$ linear von $x_1$ und $x_2$ abhängen (diese Abhängigkeit wird dann durch eine $2\times 2$-Matrix $A$
beschrieben), so kann man versuchen, beliebige Werte für $y_1$ und $y_2$ vorzugeben die entsprechenden Beziehungen
nach $x_1$ und $x_2$ aufzulösen, d.h. umgekehrt $x_1$ und $x_2$ in Abhängigkeit von $y_1$ und $y_2$ zu betrachten.
Gelingt das, so nennen wir die Matrix $A$ invertierbar. Diese umgedrehte Abhängigkeit ist dann ebenfalls
linear und wird durch eine $2\times 2$-Matrix beschrieben, die wir die zu $A$ inverse Matrix (kurz: die Inverse von $A$) nennen und mit
$A^{-1}$ bezeichnen.
Um die Frage, welche $2\times 2$-Matrizen invertierbar sind, zu diskutieren, ist es angebracht,
eine allgemeine $2\times 2$-Matrix zu betrachten. Wir schreiben sie in der Form
|
$A=\left(\begin{array}{cc}
A_{11} & A_{12}\\
A_{21} & A_{22}
\end{array}\right)$
|
|
|
$(25)$ |
an. (Wie bereits ganz zu Beginn erwähnt, zeigen die Indizes in dieser Schreibweise die Zeilen- und Spaltennummern an:
$A_{12}$ ist die Komponente, die in der ersten Zeile und in der zweiten Spalte der Matrix $A$ steht).
Wird versucht, die zu $A$ inverse Matrix zu berechnen, indem die lineare Abhängigkeit, die
$A$ beschreibt, rechnerisch "umgedreht" wird – wir werden das später in diesem Kapitel tun –,
so ergibt sich zunächst die Formel
|
$A^{-1}={1\over \Large A_{11}A_{22}-A_{12}A_{21}}\left(\begin{array}{cc}
A_{22} & -A_{12}\\
-A_{21} & A_{11}
\end{array}\right)$
|
. |
|
$(26)$ |
| | | |

Kehrwert
| |
| | |
Hier tritt allerdings ein Bruchterm auf. Nur wenn der Nenner von $0$ verschieden ist, d.h. wenn $A_{11}A_{22}-A_{12}A_{21}\neq 0$ gilt,
ist die Matrix $A$ invertierbar. Ihre Inverse ist dann durch (26) gegeben. Um diese Formel zu beweisen,
multiplizieren Sie einfach die Matrizen (25) und (26),
egal in welcher Reihenfolge (siehe nebenstehenden Button)!
In beiden Fällen werden Sie
als Ergebnis die $2\times 2$-Einheitsmatrix (23) finden.
Analoges gilt für quadratische Matrizen in höheren Dimensionen: Ganz allgemein bezeichnen wir eine $n\times n$-Matrix $A$ als invertierbar,
wenn es eine $n\times n$-Matrix $C$ gibt, so dass $AC=CA=\mathbf{1}$ gilt. Wir bezeichnen $C$ dann als $A^{-1}$ und nennen sie die zu $A$
inverse Matrix. (Ergänzend sei hinzugefügt, dass dafür auch eine einzige der beiden Bedingungen $AC=\mathbf{1}$
und $CA=\mathbf{1}$ ausreicht. Die zweite folgt dann automatisch).
Die Formel für die Inverse einer Matrix wird in höheren Dimensionen aber recht schnell sehr kompliziert, so dass wir
hier darauf verzichten, uns aber merken wollen: Für jede invertierbare quadratische Matrix jeder Dimension gilt
|
$A^{-1}A=AA^{-1}=\mathbf{1}$
|
. |
|
$(27)$ |
Ohne Beweis erwähnen wir,
- dass eine $n\times n$-Matrix genau dann invertierbar ist, wenn ihre Spalten – als Vektoren aufgefasst – den
gesamten $\mathbb{R}^n$ "aufspannen", d.h. wenn jedes Element des $\mathbb{R}^n$ als Linearkombination dieser
$n$ Vektoren dargestellt werden kann,
- und dass die Inverse eines Produkts zweier invertierbarer Matrizen $A$ und $B$ der gleichen Dimension
gleich dem Produkt der Inversen in umgekehrter Reihenfolge ist: $(AB)^{-1}=B^{-1}A^{-1}$.
Das Konzept der inversen Matrix ist insbesondere beim Lösen linearer Gleichungssysteme, deren Zusammenhang mit der Matrizenrechnung
weiter unten besprochen wird, nützlich.
| | | |
| |
| | |
Determinante
Die Determinante einer quadratischen Matrix $A$ ist eine nützliche Größe, die angibt, ob $A$ invertierbar ist oder nicht.
In zwei Dimensionen, d.h. für eine Matrix der Form (25), ist die Determinante durch den in (26)
auftretenden Nenner gegeben, d.h.
|
$\det(A)=A_{11}A_{22}-A_{12}A_{21}$
|
. |
|
$(28)$ |
Die Matrix $A$ ist genau dann invertierbar, wenn $\det(A)\neq 0$ ist.
Hier ein Beispiel:
|
$\det\left(\begin{array}{cc}
2 & 3\\
-1 & 4
\end{array}\right) \equiv \left|\begin{array}{cc}
2 & 3\\
-1 & 4
\end{array}\right| = 2\cdot 4-3\cdot(-1)= 8 + 3 = 11$
|
. |
|
$(29)$ |
Wie hieraus ersichtlich, kann die Determinante auch mit zwei senkrechten Strichen statt der Matrix-Klammern
angeschrieben werden.
Geometrisch interpretiert, ist die Determinante einer $2\times 2$-Matrix gerade der orientierte Flächeninhalt des
aus seinen Spalten(vektoren) gebildeten Parallelogramms. "Orientiert" bedeutet hier: Der Flächeninhalt wird als
positiv (negativ) aufgefasst, wenn die Drehung mit Winkel $\leq 180^\circ$, die den ersten Spaltenvektor in den
zweiten überführt, im Gegenuhrzeigersinn (Uhrzeigersinn) erfolgt.
Das Konzept der Determinante kann auf beliebige Dimensionen übertragen werden.
Ganz allgemein gilt, dass eine quadratische Matrix genau dann invertierbar ist, wenn $\det(A)\neq 0$ gilt.
In drei Dimensionen, wenn die Matrix $A$ in der Form
|
$A=\left(\begin{array}{ccc}
A_{11} & A_{12} & A_{13}\\
A_{21} & A_{22} & A_{23}\\
A_{31} & A_{32} & A_{33}
\end{array}\right)$
|
|
|
$(30)$ |
angeschrieben wird, kann die Determinante mit Hilfe der Formel
|
\begin{eqnarray}
\det(A) &=& A_{11}A_{22}A_{33}+A_{31}A_{12}A_{23}+A_{13}A_{21}A_{32}\\
&& -A_{31}A_{22}A_{13}-A_{11}A_{32}A_{23}-A_{33}A_{21}A_{12}
\end{eqnarray}
|
|
|
$(31)$ |
berechnet werden (eine Formel, die auch als Regel von Sarrus bekannt ist – wir sind ihr im Kapitel über Gleichungssysteme
bereits begegnet). Die Determinante in drei Dimensionen ist gleich dem orientierten Volumsinhalt des von den drei
Spalten(vektoren) der Matrix gebildeten Parallelepipeds, eine Idee, die sich auch auf höhere Dimensionen verallgemeinern lässt.
Wie die Determinante in Dimensionen $> 3$ berechnet wird, erfordert mehr Theorie und ist einem späteren Kapitel vorbehalten.
Die Determinante der Einheitsmatrix ist (in jeder Dimension) gleich $1$.
Ohne Beweis erwähnen wir, dass stets $\det(AB)=\det(A)\det(B)$ gilt. Mit $\det(\mathbf{1})=1$ folgt daraus, dass die
Determinante der Inversen einer Matrix gleich dem Kehrwert der Determinante ist:
$\det(A^{-1})=\det(A)^{-1}$.
| | | |

Regel von Sarrus

(in Vorbereitung)
Determinante
| |
| | |
Transponierte Matrix
Manchmal ist es beim Rechnen mit Matrizen von Vorteil, aus einer gegebenen Matrix $A$ eine andere Matrix
zu gewinnen, die durch Vertauschung der Zeilen- und Spaltennummern entsteht. Diese neue Matrix heißt die
zu $A$ transponierte Matrix (kurz: die Transponierte von $A$) und wird mit $A^T$ (manchmal auch $A^t$) bezeichnet.
Hier ein Beipiel:
|
$A=\left(\begin{array}{cc}
1 & -2\\
4 & 0\\
3 & 1
\end{array}\right)
$, daher
$A^T=\left(\begin{array}{ccc}
1 & 4 & 3\\
-2 & 0 & 1
\end{array}\right)
$
|
. |
|
$(32)$ |
Ohne Beweis erwähnen wir,
- dass die Transponierte eines Produkts zweier Matrizen
gleich dem Produkt der Transponierten in umgekehrter Reihenfolge ist: $(AB)^T=B^TA^T$,
- dass für jede quadratische Matrix $\det(A^T)=\det(A)$ gilt,
- und dass für jede invertierbare Matrix $(A^T)^{-1}=(A^{-1})^T$ gilt.
| | | |
| |
| | |
Mit Hilfe der transponierten Matrix kann das Skalarprodukt zweier Spaltenvektoren $u$ und $v$
einfach in der Form (hier anhand eines dreidimensionalen Beispiels)
|
$u^T v=\left(\begin{array}{ccc}
u_1 & u_2 & u_3
\end{array}\right)\left(\begin{array}{c}
v_1 \\ v_2 \\ v_3
\end{array}\right)= u_1 v_1 + u_2 v_2 + u_3 v_3
$
|
|
|
$(33)$ |
geschrieben werden.
| | | |

Skalarprodukt
| |
| | |
Geometrische Beispiele
Wie bisher ausführlich dargestellt, können Matrizen als Ausdruck linearer Abhängigkeiten betrachtet werden,
also etwa $y_1$ und $y_2$ in Abhängigkeit von $x_1$ und $x_2$. Werden dann konkrete Werte für $x_1$ und $x_2$
vorgegeben, so können die Werte von $y_1$ und $y_2$ im Matrixformalismus in der Form $y=Ax$ berechnet werden. Dieser Sachverhalt kann auch als
lineare Abbildung (Funktion, Zuordnung) interpretiert werden:
Jedem zweidimensionalen Vektor $x$ (der ja nichts weiter als ein Zahlenpaar, also ein Element der Menge $\mathbb{R}^2$ ist)
wird ein Vektor $y$ (also ebenfalls ein Zahlenpaar, d.h. ein Element von $\mathbb{R}^2$) zugeordnet:
|
\begin{eqnarray}
A &:& \mathbb{R}^2\rightarrow \mathbb{R}^2\\
A &:& x\mapsto Ax
\end{eqnarray}
|
. |
|
$(34)$ |
Die Zuordnungsvorschrift (die "Funktion") bezeichnen wir der Einfachheit halber mit dem gleichen Buchstaben
wie die Matrix, in diesem Beispiel also mit $A$. Ganz analog kann eine $n\times n$-Matrix als lineare
Abbildung $\mathbb{R}^n\rightarrow \mathbb{R}^n$ verstanden werden (und eine $m\times n$-Matrix als lineare
Abbildung $\mathbb{R}^n\rightarrow \mathbb{R}^m$).
Lineare Abbildungen zeichnen sich dadurch aus, dass sie Linearkombinationen "respektieren", d.h. dass für
beliebige Vektoren $x$, $x'$ und beliebige Zahlen $a$, $a'$ stets
gilt – eine Eigenschaft, die beim korrekten Umgang mit Klammern beim Rechnen mit Matrizen automatisch
berücksichtigt ist.
| | | |

Funktion (Abbildung)

Zahlenpaar
| |
| | |
Wir beschränken uns im Folgenden auf $2\times 2$-Matrizen als Darstellungen linearer Abbildungen
$\mathbb{R}^2\rightarrow \mathbb{R}^2$.
Da ein Element des $\mathbb{R}^2$ als Punkt der Zeichenebene interpretiert werden kann,
erhalten $2\times 2$-Matrizen auf diese Weise eine geometrische Bedeutung (ähnlich wie Vektoren als Pfeile
interpretiert werden können).
Wir wollen nun drei Typen von Abbildungen besprechen, die auf diese Weise durch Matrizen dargestellt
werden können.
Eine der einfachsten linearen Abbildungen des $\mathbb{R}^2$ ist die Spiegegung an der $x_1$-Achse:
Wird irgendein Punkt, dessen Ortsvektor durch
|
$x=\left(\begin{array}{c}
x_1 \\ x_2
\end{array}\right)$
|
|
|
$(36)$ |
gegeben ist, an der $x_1$-Achse gespiegelt, so ist der Ortsvektor des gespiegelten Punktes
gleich
|
$x_{\sf gespiegelt}=\left(\begin{array}{c}
x_1 \\ -x_2
\end{array}\right)$
|
. |
|
$(37)$ |
Hier eine Skizze dieses Sachverhalts:
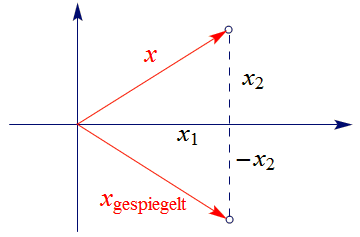
Die Abbildung $S$, die $x$ in $x_{\sf gespiegelt}$ überführt, die also
$S:x\mapsto x_{\sf gespiegelt}$ bewirkt, ist linear. Sie wird durch die Matrix
|
$S=\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)$
|
|
|
$(38)$ |
dargestellt. Davon können Sie sich leicht selbst überzeugen:
|
$S\,x=\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\left(\begin{array}{c}
x_1 \\
x_2
\end{array}\right)=\left(\begin{array}{c}
x_1 \\
-x_2
\end{array}\right)=x_{\sf gespiegelt}$
|
. |
|
$(39)$ |
| | | |

R2
| |
| | |
Analog kann auch die Spiegelung an der $x_2$-Achse und, mit ein bisschen mehr Aufwand, Spiegelungen an
beliebigen durch den Ursprung verlaufenden Geraden mit Hilfe von Matrizen dargestellt werden
(siehe den nebenstehenden Button).
Ein weiterer Typ von linearen Abbildungen sind die Projektionen. Stellen wir uns vor, in der Zeichenebene scheint die
Sonne von "oben", so dass jeder Punkt, der "oberhalb" der $x_1$-Achse liegt, einen "Schatten" auf diese Achse wirft.
Ist $x$ der Orstvektor des gegebenen Punktes, so wird $x_{\sf projiziert}$ erhalten, indem die $x_1$-Koordinate belassen und
die $x_2$-Koordinate gleich $0$ gesetzt wird. Diese Regel wollen wir für
alle Punkte der Zeichenebene vereinbaren, also auch für jene, die "unterhalb" der $x_1$-Achse liegen. Damit ist ein
Beispiel einer Projektion definiert.
Hier eine Skizze dieses Sachverhalts:
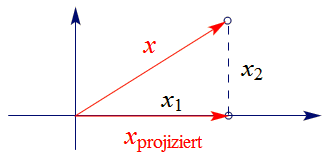
Die Abbildung $P:x\mapsto x_{\sf projiziert}$ ist ebenfalls linear,
und ihre Matrix ist durch
|
$P=\left(\begin{array}{cc}
1 & 0 \\
0 & 0
\end{array}\right)$
|
|
|
$(40)$ |
gegeben, denn es gilt
|
$P\,x=\left(\begin{array}{cc}
1 & 0 \\
0 &0
\end{array}\right)\left(\begin{array}{c}
x_1 \\
x_2
\end{array}\right)=\left(\begin{array}{c}
x_1 \\
0
\end{array}\right)=x_{\sf projiziert}$
|
. |
|
$(41)$ |
Für diese Matrix gilt $P^2=P$ (rechnen Sie nach!), was einfach aussagt, dass die zweifache Anwendung einer Projektion nichts anderes
bewirkt als die einfache (oder, bildlich gesprochen, dass der Schatten eines Schattens der Schatten selbst ist).
Schließlich sind auch Drehungen (Rotationen) um den Ursprung lineare Abbldungen und können daher durch Matrizen
dargestellt werden. Die Matrix einer Drehung im Gegenuhrzeigersinn um den
Winkel ist $\alpha$ durch
|
$R=\left(\begin{array}{cc}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{array}\right)$
|
|
|
$(42)$ |
| | | |
an einer beliebigen
Geraden
| |
| | |
gegeben. Jeder beliebige Vektor $x$ wird durch $R:x\mapsto R\,x = x_{\sf gedreht}$ in den entsprechend gedrehten Vektor übergeführt,
wie die Skizze illustriert:
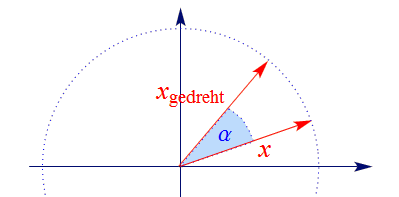
Es ist ganz leicht, zu überprüfen, dass der Vektor $\left(\begin{array}{c}1\\0\end{array}\right)$ durch
(42) tatsächlich in einen um den Winkel $\alpha$ gedrehten Vektor
übergeführt wird. (Für den Beweis, dass $R$ alle Vektoren in der gewünschten Weise
dreht, siehe den nebenstehenden Button).
| | | |
um einen
gegebenen Winkel
| |
| | |
Komplexe Matrizen
Matrizen können durchaus auch komplexe Zahlen als Komponenten enthalten.
Alle Strukturen und Operationen sehen dann ganz genauso aus und funktionieren ganz gleich
wir bisher besprochen, wenn $\mathbb{C}^n$ anstelle von $\mathbb{R}^n$ geschrieben wird.
Lediglich die geometrische Interpretation von Vektoren ist dann nicht mehr in der gleichen Weise möglich, und
das Skalarprodukt (33) wird üblicherweise
nicht für komplexe Vektoren verwendet, sondern durch das so genannte innere Produkt
$u^\dagger v$ ersetzt, wobei $u^\dagger$ aus $u^T$ entsteht, indem alle Komponenten komplex konjugiert werden.
Generell kann für jede komplexe Matrix die adjungierte (auch hermitisch konjugierte) Matrix
(ausgesprochen "$A$ dagger", von engl. dagger = Dolch) definiert werden. Für reelle Matrizen gilt
natürlich $A^\dagger=A^T$.
|
| | |

komplexe Zahlen

komplex konjugiert
| |
| | |
| Matrizen und lineare Gleichungssysteme |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Lineare Gleichungssysteme in Matrixform
Den linearen Gleichungssystemen, ihrer geometrischen Interpretation, Lösungsverfahren und Lösungsfällen ist im
Kapitel über Gleichungssystem breiter Raum gewidmet. Sie sollten die dort besprochenen Sachverhalte zumindest in
Grundzügen kennen. Wir werden im Folgenden nur jene Aspekte besprechen, die durch die Verwendung
von Matrizen hinzu kommen.
Bisher haben wir in diesem Kapitel mit dem Begriff "linear" immer "linear-homogen" gemeint, Ab jetzt müssen
wir genauer zwischen den Begriffen "linear-homogen" und "linear-inhomogen" unterscheiden. Als "lineares Gleichungssystem"
von $m$ Gleichungen in $n$ Variablen $x_1$, $x_2$,... $x_n$ verstehen wir ein Gleichungssystem der Form
|
\begin{eqnarray}
A_{11}x_1 + A_{12}x_2+\dots+A_{1n}x_n&=&c_1\\
A_{21}x_1 + A_{22}x_2+\dots+A_{2n}x_n&=&c_2\\
.....................\\
A_{m1}x_1 + A_{m2}x_2+\dots+A_{mn}x_n&=&c_m\\
\end{eqnarray}
|
|
|
$(44)$ |
Dabei sind die Koeffizienzen $A_{jk}$ und die Zahlen $c_j$ gegeben. Sind alle $c_j=0$, so nennen wir das System homogen,
andernfalls heißt es inhomogen.
Wir können ein solches Gleichungssystem sofort in Matrixschreibweise bringen, indem wir die $A_{jk}$ zu einer $m\times n$-Matrix $A$
zusammenfassen und
|
$x=\left(\begin{array}{c}
x_1\\
x_2\\
\vdots\\
x_n
\end{array}\right)
{\sf,}\qquad
c=\left(\begin{array}{c}
c_1\\
c_2\\
\vdots\\
c_m
\end{array}\right)
$
|
|
|
$(45)$ |
definieren. Es lautet dann kurz und bündig
| | | |

Gleichungssysteme
| |
| | |
Das Problem besteht darin, die Lösungsmenge, d.h. die Menge aller Vektoren $x$, die
(46) erfüllen, zu bestimmen. Von besonderem Interesse ist die Frage, wann es
überhaupt eine Lösung gibt, wann es genau eine Lösung gibt und wann es unendlich viele Lösungen gibt.
(Wie im Kapitel über Gleichungssysteme besprochen, sind das die Lösungsfälle, die
auftreten können).
Wir werden uns bei der Diskussion dieser Fragen auf den Fall $m=n$ beschränken, d.h. auf den Fall, dass es gleich viele Variable
wie Gleichungen gibt (oder, anders ausgedrückt, dass die Matrix $A$ quadratisch ist).
Wir betrachten also ein lineares Gleichungssystem der Form (46), wobei
$A$ eine $n\times n$-Matrix ist. Ist $c\neq 0$, so ist das Gleichungssystem inhomogen, und dann nennen wir
das zugehörige homogene Gleichungssystem.
| | | |

Lösungsfälle
| |
| | |
Um ein lineares Gleichungssystem rechnerisch zu lösen, gibt es eine Reihe von Methoden.
Wenden wir sie an, so finden wir einen von drei grundsätzlichen Lösungsfällen:
- Am Ende ergibt sich eine eindeutige Lösung $x$.
- Es ergibt sich ein Widerspruch (etwa $0=1$). In diesem Fall besitzt das Gleichungssystem keine Lösung.
- Am Ende bleiben eine oder mehrere Beziehungen zwischen den Variablen übrig.
In zwei Dimensionen kann eine solche Beziehung als Geradengleichung interpretiert werden, in drei Dimensionen als Ebenengleichung.
In einem solchen Fall besitzt das Gleichungssystem unendlich viele Lösungen (die in zwei Dimensionen eine Gerade, in drei
Dimensionen eine Gerade oder eine Ebene bilden). Ein Extremfall ergibt sich, falls $A=0$ und $c=0$ ist. In diesem Fall gibt
es überhaupt keine nichttriviale Gleichung, so dass jeder Vektor $x$ Lösung ist.
Wie es nun weitergeht, hängt davon ab, ob die Matrix $A$ invertierbar ist.
| | | |

lineare
Gleichungssysteme
rechnerisch lösen
| |
| | |
Wenn $A$ invertierbar ist – und wie die Inverse berechnet werden kann
Ist die Matrix $A$ invertierbar, so hilft das Konzept der inversen Matrix, das lineare Gleichungssystem (46)
mit einem Schlag zu lösen:
|
Satz: Ist $A$ invertierbar, d.h. gilt $\det(A)\neq 0$, so besitzt das Gleichungssystem $Ax=c$ genau eine Lösung,
nämlich $x=A^{-1}c$.
|
Beweis: Ist $A$ invertierbar, so können wir beiden Seiten der (Matrix-)Gleichung
$Ax=c$ von links mit $A^{-1}$ multiplizieren und erhalten $A^{-1}Ax=A^{-1}c$. Da $A^{-1}A=\mathbf{1}$ gilt und stets $\mathbf{1}x=x$ ist,
folgt $x=A^{-1}c$. Damit ist die (eindeutige) Lösung gefunden.
Wenn wir also die Inverse $A^{-1}$ kennen, so erhalten wir die Lösung ohne großen Aufwand, indem einfach $A^{-1}$ mit $c$
multipliziert wird! Für den homogenen Fall ($c=0$) folgt daraus sofort, dass (46) nur die triviale Lösung $x=0$
besitzt.
Aber wie berechnen wir die Inverse? In der Praxis
- wird die Inverse einer $2\times 2$-Matrix mit Hilfe der einfachen Formel (26) berechnet,
- die Inverse einer höherdimensionalen Matrix am Computer (wir werden weiter unten ein paar Computerwerkzeuge vorstellen).
| | | |
| |
| | |
Es ist aber für das Verständnis nützlich, zu wissen, wie die Inverse im Prinzip auch
"händisch" ermittelt werden kann. Wir haben alle Voraussetzungen dafür bereits kennen gelernt.
Es gibt einige Algorithmen zur Berechnung der Inversen, die aber alle auf die gleiche Grundidee hinauslaufen:
Lösen Sie das Gleichungssystem $Ax=c$ mit Ihrer Lieblingsmethode (im Kapitel über Gleichungssysteme wurden das
Eliminationsverfahren und das Substitutionsverfahren besprochen), belassen dabei aber den Vektor $c$ ganz allgemein,
ohne konkrete Zahlen als Komponenten für ihn anzunehmen. Wie auch immer Sie es im Detail machen – am Ende ergeben sich
Lösungsformeln für die Komponenten der (eindeutig bestimmten) Lösung $x$. Diese haben die Form
einer linearen Abhängigkeit, aus der unmittelbar die Komponenten von $A^{-1}$ abgelesen werden können.
Damit wurde nichts anderes gemacht als die lineare Abhängigkeit $c=Ax$ zu $x=A^{-1}c$ umzukehren!
Wir demonstrieren das anhand eines Beispiels in zwei Dimensionen: Gegeben sei die Matrix
|
$A=\left(\begin{array}{cc}
3 & 2 \\
5 & -4
\end{array}\right)$
|
. |
|
$(48)$ |
Wir lösen das Gleichungssystem
|
\begin{eqnarray}
3x_1+2x_2&=&c_1\\
5x_1-4x_2 &=&c_2
\end{eqnarray}
|
|
|
$(49)$ |
mit dem Substitutionsverfahren: Aus der ersten Gleichung folgt $x_2=-{3\over 2}x_1+{1\over 2}c_1$. Dies wird in die
zweite Gleichung eingesetzt, womit sich $5x_1-4\left(-{3\over 2}x_1+{1\over 2}c_1\right) = c_2$ ergibt. Diese Gleichung kann
sofort nach $x_1$ gelöst werden, und mit dem Ergebnis können wir $x_2$ bestimmen. Die Lösung lautet
|
\begin{eqnarray}
x_1&=&{2\over 11}c_1+{1\over 11}c_2\\
x_2 &=&{5\over 12}c_1-{3\over 33}c_2
\end{eqnarray}
|
. |
|
$(50)$ |
| | | |

Eliminations-
verfahren

Substitutions-
verfahren
| |
| | |
Damit können die Kompoonenten der Inversen abgelesen werden:
|
$A^{-1}=\left(\begin{array}{cc}
{2\over 11} & {1\over 11} \\
{5\over 22} & -{3\over 22}
\end{array}\right)\,\,\equiv\,\,{1\over 22}\left(\begin{array}{cc}
4 & 2 \\
5 & -3
\end{array}\right)$
|
, |
|
$(51)$ |
wobei wir als letzten Schritt noch eine kleine Vereinfachung vorgenommen haben.
Überprüfen Sie, ob Sie mit Formel (26) zum gleichen Ergebnis
gelangen!
Mit der gleichen Methode kann die Formel (26) für die Inverse einer
(invertierbaren) $2\times 2$-Matrix ganz allgemein hergeleitet werden (siehe den nebenstehenden Button).
In höheren Dimensionen funktioniert die Ermittlung der Inversen im Prinzip genauso, ist aber entsprechend aufwändiger
(und fehleranfälliger – weshalb wir die Berechnung in diesen Fällen besser
dem Computer übergeben).
| | | |
einer 2×2-Matrix
| |
| | |
Wenn $A$ nicht invertierbar ist: homogener Fall
Ist die $n\times n$-Matrix $A$ nicht invertierbar, so müssen wir zwischen dem homogenen und dem inhomogenen Fall unterscheiden:
Zunächst der homogene Fall:
|
Satz: Ist $A$ nicht invertierbar, d.h. gilt $\det(A)=0$, so besitzt das Gleichungssystem $Ax=0$ unendlich viele
Lösungen.
|
Beweis(idee): Nach unserer Definition der Invertierbarkeit ist eine Matrix $A$ invertierbar, wenn die lineare
Abhängigkeit $y=Ax$ "umgekehrt" werden kann, d.h. wenn es für jedes $y\in\mathbb{R}^n$ genau ein $x\in\mathbb{R}^n$ gibt,
für das $y=Ax$ gilt. Es sind nun zwei Gründe dafür denkbar, dass das nicht der Fall ist, d.h. dass $A$ nicht invertierbar ist:
Entweder es gibt für ein $y$ mehrere solche $x$ oder es gibt gar keines.
- Im ersten Fall genügen uns zwei verschiedene Vektoren $x'$ und $x''$, für die $y=Ax'$ und $y=Ax''$ gilt.
Es gilt dann $Ax'=Ax''$, woraus $A(x'-x'')=0$ folgt, womit eine Lösung $x=x'-x''\neq 0$ des Gleichungssystems
$Ax=0$ gefunden ist. Dann ist aber auch jedes Vielfache von $x$ eine Lösung, womit unendlich viele Lösungen gefunden sind.
- Der zweiten Fall bedeutet, dass es ein $y$ gibt, das überhaupt nicht in der Form $y=Ax$ geschrieben
werden kann. Das impliziert, dass die Menge aller Vektoren der Form $Ax$ nicht der ganze $\mathbb{R}^n$ ist, sondern
nur eine Teilmenge dieses Raumes. Nun lässt sich (mit Methoden, die uns hier nicht zur Verfügung stehen) zeigen,
dass es auch in diesem Fall verschiedene Vektoren $x'$ und $x''$ gibt, für die $Ax'=Ax''$ gilt.
Der Grund dafür liegt, bildlich gesprochen, darin, dass $A$ den ganzen $\mathbb{R}^n$ auf eine Teilmenge des $\mathbb{R}^n$
(niedrigerer Dimension) abbbildet, und dass in dieser Teilmenge "nicht genug Platz" dafür ist,
dass alle $Ax$ voneinander verschieden wären.

Anmerkung: Diese Aussage kann auch so formuliert werden: Eine lineare Abbildung
$A:\mathbb{R}^n\rightarrow\mathbb{R}^n$ ist entweder gleichzeitig injektiv, surjektiv und bijektiv (dann ist sie invertierbar) oder keins davon.
Aber Achtung: Diese besondere Eigenschaft gilt für lineare Abbildungen – sie kann nicht auf
Abbildungen generell übertragen werden!
| | | |

injektiv, surjektiv,
bijektiv
| |
| | |
Tatsächlich treten bei nicht-invertierbaren Matrizen immer beide in der obigen Argumentation genannten Fälle gleichzeitig auf:
Ist $A$ eine nicht.invertierbare $n\times n$-Matrix,
- so gibt es verschiedene Vektoren im $\mathbb{R}^n$, die durch $A$ auf das gleiche Element abgebildet werden
(was bedeutet, dass $A$ nicht injektiv ist), und daher gibt es unendlich viele Lösungen des Gleichungssystems $Ax=0$,
- und es gibt Vektoren im $\mathbb{R}^n$, die in der Menge aller $Ax$ (d.h. im Bild von $A$) nicht vorkommen
(was bedeutet, dass $A$ nicht surjektiv ist).
Die Lösungsmenge eines homogenen linearen Gleichungssystems $Ax=0$ besitzt die Eigenschaft, dass jede Linearkombination von
Lösungen wieder eine Lösung ist. Sind $\hat{x}$ und $\tilde{x}$ Lösungen, d.h. gilt
$A\hat{x}=0$ und $A\tilde{x}=0$, so ist beispielsweise auch $3\hat{x}-5\tilde{x}$ eine Lösung, da
$A(3\hat{x}-5\tilde{x})=3\,\underbrace{A\hat{x}}_{\large 0}-5\,\underbrace{A\tilde{x}}_{\large 0}=0$.
Und falls $A$ nicht invertierbar ist, so besteht die Lösungsmenge gemäß dem
obigen Satz aus unendlich vielen Elementen. Damit lassen sich einige grundsätzliche Aussagen machen:
- Im $\mathbb{R}^2$ gibt es nur zwei Typen von Mengen, die alle diese Eigenschaften besitzen: Geraden durch den Ursprung
und den $\mathbb{R}^2$ selbst.
- Im $\mathbb{R}^3$ gibt es nur drei Typen von Mengen, die alle diese Eigenschaften besitzen: Geraden durch den Ursprung,
Ebenen, in denen der Ursprung liegt, und den $\mathbb{R}^3$ selbst.
- In einem höher-dimensionalen $\mathbb{R}^n$ können wir uns die Verhältnisse nicht mehr bildlich vorstellen,
aber im Prinzip gibt es auch dort mehrere (nämlich $n$) Typen derartiger Mengen.
All diese Mengen können als Lösungsmengen homogener linearer Gleichungssysteme mit nicht invertierbarer Matrix
auftreten.
| | | |

Bild (Wertebereich)
| |
| | |
Wenn $A$ nicht invertierbar ist: inhomogener Fall
Nun kommen wir zum inhomogenen Fall, d.h. zu Gleichungssystemen der Form $Ax=c$ mit $c\neq 0$ und nicht invertierbarer Matrix $A$.
Da kann einerseits der Fall eintreten, dass es überhaupt keine Lösung gibt: Wir wissen ja bereits, dass es Vektoren gibt,
die in der Menge der $Ax$ nicht vorkommen. Ist $c$ ein solcher Vektor, so besitzt das Gleichungssystem $Ax=c$ keine Lösung.
Rechnerisch zeigt sich das daran, dass beim Versuch, es zu lösen, ein Widerspruch auftritt.
Andererseits kann der Fall eintreten dass die Lösungsmenge nicht-leer ist, und dann gibt es gleich unendlich viele
Lösungen. Eine genauere Aussage erhalten wir mit einem Trick: Bezeichnen wir mit $x_{\sf inh}$ irgend eine Lösung des
inhomogenen Gleichungssystems. Ist dann $x_{\sf hom}$ eine Lösung des zugehörigen homogenen Gleichungssystems,
d.h. gilt $Ax_{\sf hom}=0$, so ist $x_{\sf inh} + x_{\sf hom}$ eine weitere Lösung des inhomogenen Gleichungssystems:
|
$A(x_{\sf inh} + x_{\sf hom})=\underbrace{Ax_{\sf inh}}_{\Large c} + \underbrace{Ax_{\sf hom}}_{\large 0} = c\,$
|
. |
|
$(52)$ |
Damit haben wir schon unendlich viele Lösungen des inhomogenen Gleichungssystems gefunden. Zum Abschluss zeigen wir, dass
wir damit auch schon alle gefunden haben: Ist $x_{{\sf inh},2}$ irgendeine Lösung des inhomogenen Gleichungssystems, so gilt
|
$A(x_{\sf inh} - x_{{\sf inh},2})=\underbrace{Ax_{\sf inh}}_{\Large c} - \underbrace{Ax_{{\sf inh}_2}}_{\Large c} = 0\,{\sf\small,}$
|
|
|
$(53)$ |
was nichts anderes besagt, als dass die Differenz $x_{\sf inh} - x_{{\sf inh},2}$ eine Lösung des homogenen Gleichungssystems
ist. Daher ist
$x_{{\sf inh},2} = x_{\sf inh} +$ eine Lösung des homogenen Gleichungssystems
und damit von der Form $x_{\sf inh} + x_{\sf hom}$. Fassen wir diese Erkenntnisse zusammen:
Satz: Ist die Lösungsmenge des inhomogenen linearen Gleichungssystems $Ax=c$ nicht-leer, und ist
$x_{\sf inh}$ eine spezielle (festgehaltene) Lösung, so besteht die Lösungsmenge aus allen Vektoren der Form
$x = x_{\sf inh} + x_{\sf hom}\,$,
wobei $x_{\sf hom}$ eine Lösung des zugehörigen homogenen Gleichungssystems ist.
|
Der Satz gilt ganz allgemein, so wie er formuliert ist – im gegenwärtigen Zusammenhang ist er insbesondere
für $c\neq 0$ und $A$ nicht-invertierbar interessant.
Geometrisch kann die Lösungsmenge eines solchen Gleichungssystems als "verschobene" Variante der Lösungsmenge
des zugehörigen homogenen Gleichungssystems gedeutet werden, wie diese schematische Skizze illustriert:
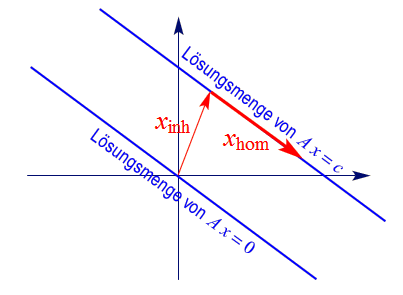
Konkret handelt es sich dabei
- im $\mathbb{R}^2$ um Geraden, die nicht durch den Ursprung gehen
- und im $\mathbb{R}^3$ um Geraden, die nicht durch den Ursprung gehen, oder um Ebenen, auf denen der Ursprung nicht liegt,
also um genau die Mengen, die bereits im Kapitel über Gleichungssysteme als geometrische Deutungen
der Lösungsmengen identifiziert wurden.
| | | |

lineare
Gleichungssysteme
geometrisch
interpretieren
| |
| | |
Rang einer Matrix
Wann immer die Lösungsmenge eines homogenen linearen Gleichungssystems unendlich viele Elemente besitzt,
kann sie als "gerades" (oder "lineares") Gebilde, auf dem der Ursprung liegt, interpretiert werden – also als Gerade, als Ebene oder
als entsprechende höherdimensionale Menge. Ganz allgemein kann jede solche Lösungsmenge durch eine Dimension
charakterisiert werden. (Geraden sind 1-dimensional, Ebenen sind 2-dimensional, ...). Können wir über diese
Dimension im Rahmen der allgemeinen Theorie genauere Ausagen machen?
Ist $A$ eine $n\times n$-Matrix, so hängt die Dimension der Lösungsmenge des Gleichungssystems $Ax=0$
nur von $A$ ab. Als den Rang der Matrix $A$ bezeichnen wir die Differenz
$n-$ Dimension der Lösungsmenge$\,$.
Er ist – ein bisschen salopp formuliert – gleich der Anzahl der Spalten (oder Zeilen) von $A$, die nicht als
Linearkombinationen anderer Spalten (oder Zeilen) ausgedrückt werden können. Ist er bekannt, so ist die
Dimension der Lösungsmenge gleich der Differenz $n-$ Rang der Matrix.
Spezialfälle sind:
- Eine $n\times n$-Matrix ist genau dann invertierbar, wenn ihr Rang gleich $n$ ist.
- Die einzige $n\times n$-Matrix, deren Rang gleich $0$ ist, ist die $n\times n$-Nullmatrix.
Der Rang von $A$ ist gleich der so genannten Kodimension der Lösungsmenge
(d.h. der Zahl, die "der Dimension der Lösungsmenge auf die Dimension des ganzen Raums fehlt").
Damit haben wir die wichtigsten Fakten über Lösungsfälle und Lösungsmengen linearer
Gleichungssysteme in der Sprache der Matrizenrechnung ausgedrückt. Sie zeigen, dass das Konzept der Matrix
ein ziemlich mächtiges ist, und sie können sowohl bei theoretischen Fragestellungen als auch beim
konkreten Rechnen helfen.
|
| | |
| |
| | |
| Matrizenrechnen mit dem Computer |
| | | |
Zum Seitenanfang | |
| | |
Zum Abschluss wollen wir nicht unerwähnt lassen, dass für Berechnungen mit Matrizen
(also Matrizen miteinander multiplizieren, die Determinante, die Inverse und den Rang einer
Matrix berechnen und – als Anwendung – lineare Gleichungssysteme lösen)
zahlreiche elektronischer Tools zur Verfügung stehen. Einige derartige Berechnungen können mit unserem Tool
Online-Rechnen mit Mathematica
durchgeführt werden:
- Wählen Sie die Kategorie "Matrizen"!
- Eine Matrix muss als Liste ihrer Zeilen eingegeben werden, wobei jede Zeile wieder eine Liste ist
(also insgesamt als Liste von Listen, jeweils mit geschwungenen Klammern angegeben). Beispielsweise wird die Matrix $$\left(\begin{array}{cc}
1 & 2\\
3 & 4
\end{array}\right)$$
in der Form {{1,2},{3,4}}
eingegeben. Die Ausgabe von Matrizen erfolgt ebenfalls in dieser Form. Matrizen können beliebige Dimension haben, und ihre
Komponenten können sowohl Zahlen als auch Terme sein.
- Die Matrizenmultiplikation wird mit einem Punkt eingegeben. Wollen Sie etwa die obige Matrix
mit $$\left(\begin{array}{cc}
5 & 6\\
7 & 8
\end{array}\right)$$
multiplizieren, so geben Sie {{1,2},{3,4}}.{{5,6},{7,8}} ein
und klicken (ohne eine Operation ausgewählt zu haben) auf "Ausführen".
Wichtig ist, dass der Punkt nicht weggelassen wird, denn sonst multipliziert Mathematica einfach die Listenelemente, die an den
gleichen Positionen stehen!
- Achtung: Das soeben Gesagte gilt auch für Potenzen von Matrizen. Sie müssen sie beispielsweise in der Form
{{1,2},{3,4}}.{{1,2},{3,4}} eingeben.
Fehlt der Punkt, so quadriert Mathematica lediglich die einzelnen Zahlen.
- Linearkombinationen von Matrizen (also auch Vielfache und Summen) schreiben Sie einfach wie (beispielsweise)
9{{1,2},{3,4}}+10{{5,6},{7,8}}.
- Um Operationen mit einer einzelnen Matrix auszuführen, geben Sie diese ein, wählen die gewünschte
Operation aus und klicken auf "Ausführen". Neben den in diesem Kapitel besprochenen sind noch einige
weitere Operationen möglich, die Sie bei Bedarf ebenfalls benutzen können. Hiervon seien nur zwei erwähnt:
- Die Spur einer quadratischen Matrix ist die Summe ihrer Diagonalelemente (also
$A_{11}+A_{22}+\dots+A_{nn}$).
- Der Nullraum einer Matrix $A$ ist der Lösungsraum des homogenen linearen Gleichungssystems
$Ax=0$. Mathematica gibt eine Liste von Vektoren (ebenfalls jeweils als Liste geschrieben) aus, die – als
Spaltenvektoren interpretiert – alle $Ax=0$ erfüllen, und deren Linearkombinationen die Lösungsmenge bilden.
- Mathematica rechnet zunächst symbolisch und verwandelt rationale Zahlen wie $1/7$ nicht automatisch in
Dezimalzahlen um. Wollen Sie die numerische Version eines Ergebnisses sehen (die dann unter Umständen nur näherungsweise gilt),
so klicken Sie auf "Resultat zur weiteren Bearbeitung als neue Eingabe übernehmen", wählen die Kategorie "Zahlen",
die Operation "numerischer Wert" und klicken aus "Ausführen".
Unter den anderen am Web zur Verfügung stehenden Tools seien zwei Online-Rechner
von RECHNERonline genannt. Der
Rechner für Matrizen
erlaubt es, recht bequem mit Matrizen (einschließlich Vektoren) bis zur Dimension $5\times 5$ zu rechnen. Der
Rechner für Lineare Gleichungssysteme
kann lineare Gleichungssysteme, die in Matrizenform gegeben sind, numerisch (also näherungsweise) lösen.
Dazu müssen Sie die so genannte erweiterte Koeffizientenmatrix
eingeben. Lautet das Gleichungssystem $Ax=c$, so entsteht diese, indem $c$ als zusätzliche Spalte zu
$A$ hinzugefügt wird. Beispielsweise ist sie für
$A = \left(\begin{array}{cc}
1 & -2\\
4 & 0
\end{array}\right)\quad$ und $\quad c = \left(\begin{array}{c}
3\\
8
\end{array}\right)$
durch
$\left(\begin{array}{cc}
1 & -2 & 3\\
4 & 0 & 8
\end{array}\right)$
gegeben. Diese beiden Rechner stehen miteinander in Verbindung, d.h. es können Berechnungsergebnisse jeweils in den
anderen übernommen werden, und die Genauigkeit (Zahl der Nachkommastellen), in der die Ergebnisse angezeigt werden
sollen, kann zwischen 0 und 12 frei gewählt werden.
|
| | |
| |