| | |
| | | |
| |
| | |
| | | |
| |
| | |
Voraussetzungen und Vorbemerkungen
Im ersten Funktionenkapitel haben wir folgende Konzepte kennen gelernt:
Wir setzen sie in diesem Kapitel als bekannt voraus. Wiederholen Sie bitte die entsprechenden
Stellen bei Bedarf. (Ein erstes Betätigen eines der obigen Links
öffnet ein neues Brwowserfenster mit dem ersten Funktionenkapitel.
Wenn Sie es geöffnet lassen, wird es − ohne weitere Ladezeit −
auch von späteren Aufrufen genutzt).
| | | |

Funktionen 1
| |
| | |
Wir werden in diesem Kapitel hauptsächlich von reellen Funktionen
sprechen, d.h. von Funktionen, die entweder für alle reellen Zahlen
oder für eine Teilmenge von R
definiert sind, d.h. Funktionen vom Typ
f : R → R oder
f : A → R
mit A ⊆ R.
Weiter unten werden wir Beispiele von Funktionen besprechen, die auf anderen Mengen
definiert sind.
Ein wichtiges Thema dieses Kapitels besteht darin, Eigenschaften von Funktionen mit
Eigenschaften ihrer Graphen in Zusammenhang zu bringen. Einige
Funktionsgraphen werden in Form vorbereiteter Grafiken gezeigt. Zögern Sie bitte nicht, den
zu verwenden, wann immer Sie darüber hinaus den Graphen einer (termdefinierten) Funktion betrachen wollen.
(Falls es in Ihrem Browser Probleme mit dem Symbol ^
für die Eingabe von Potenzen gibt, so ersetzen Sie es durch
das Wort hoch).
Die Festlegung einer Funktion f kann über die Zuordnungsvorschrift
f : x → f (x)
oder in Form der Funktionsgleichung
y = f
(x) geschehen. Die Bezeichnung der
"unabhängigen" und der "abhängigen" Variablen mit den Buchstaben x
und y ist
nicht unbedingt notwendig, aber eine alte Tradition. Dementsprechend werden wir
bei der Besprechung von Graphen die "horizontale Achse ("Abszisse") als x-Achse
und die "vertikale" Achse ("Ordinate") als y-Achse
bezeichnen.
Zuletzt noch ein Begriff, der im Folgenden öfters vorkommen wird:
Eine rationale Funktion ist eine Funktion, die als Quotient zweier Polynome
geschrieben werden kann. Rationale Funktionen sind einerseits
überschaubar und relativ leicht zu studieren, andererseits
vielfälig genug, um im Mathematikunterricht eine wichtige Rolle
zu spielen.
Wenn Sie nur an einigen der im Folgenden besprochenen Konzepten interessiert sind, so überspringen
Sie die anderen oder überfliegen Sie sie grob.
| | | |

reelle Zahlen
| |
| | |
Symmetrie und Antisymmetrie
Wir nennen eine Funktion
f : R → R
symmetrisch (manchmal auch gerade), wenn für alle
x ∈ R
gilt. Der Graph einer symmetrischen Funktion ist symmetrisch bezüglich der
y-Achse (d.h. er geht unter einer
Spiegelung an der y-Achse in sich selbst über).
Weiters nennen wir eine Funktion
f : R → R
antisymmetrisch (manchmal auch ungerade), wenn für alle
x ∈ R
gilt. Der Graph einer antisymmetrischen Funktion ist symmetrisch bezüglich des
Ursprungs (d.h. er geht unter einer Punktspiegelung am Ursprung, d.h. einer Drehung um 180°, in sich selbst über).
Beide Konzepte übertragen sich zwanglos auf Funktionen, die nicht auf
ganz R definiert sind: Es muss
dann (1) bzw. (2) für alle
x ∈ A
gelten, wobei A der Definitionsbereich von
f ist.
Viele wichtige Funktionen fallen in eine der beiden Klassen:
| | | |
| |
| | |
- Beispiele für symmetrische Funktionen: xn
für gerades n
(d.h. 1, x2, x4,...),
x2−1,
1/x2, 1/x4,
1/(x2−1),
(1−x2)1/2,
cos x, sin2x,
x sin x,
cosh x (für letztere s.u.).
- Beispiele für antisymmetrische Funktionen: xn
für ungerades n
(d.h. x, x3,...),
x3−x,
1/x, 1/x3,
x/(x2−1),
x (1−x2)1/2,
sin x, x cos x,
tan x, cot x,
sinh x, tanh x, coth x (für letzte drei s.u.), sgn x (s.u.).

|
Wie aus diesen Beispielen ersichtlich ist, ist die (Anti-)Symmetrie vieler elementarer Funktionen
der schlichten Identität
(−x)2 = x2
zu verdanken, die selbst wiederum Konsequenz von
(−1)2 = 1 ist. Daher definiert ein Funktionsterm, in den
die Variable x nur quadratisch (d.h. als
x2) eingeht, immer eine symmetrische Funktion.
Das Produkt zweier symmetrischer oder zweier antisymmetrischer Funktionen
ist symmetrisch, das Produkt einer symmetrischen mit einer antisymmetrischen Funktion ist
antisymmetrisch.
Symmetrieeigenschaften von Funktionen können ausgenutzt werden, um Berechnungen
so kurz wie möglich zu halten: Ist eine Eigenschaft einer
(anti)symmetrischen Funktion (z.B. der Verlauf ihres Graphen oder die Lage einer Nullstelle) im Bereich x ≥ 0
bekannt, so ergibt sich die entsprechende Eigenschaft für den Bereich x < 0
ganz automatisch.
| | | |
| |
| | |
Periodizität
Wir nennen eine Funktion
f : R → R
periodisch, wenn es eine positive Zahl p gibt, so dass für alle
x ∈ R
gilt. p heißt dann Periode oder
Periodenlänge. Mit wachsendem x
"wiederholt sich" eine periodische Funktion immer wieder, denn die zweimalige Anwendung von (3) ergibt
f (x + 2 p)
= f (x + p) =
f (x),
und ganz allgemein gilt
f (x + n p)
= f (x)
für jede natürliche Zahl.
Mit p ist also auch jedes Vielfache
n p eine Periode,
und entsprechend weist der Graph einer periodischen Funktion ein immer wiederkehrendes Muster auf.
Das Konzept überträgt sich zwanglos auf Funktionen, die nicht auf
ganz R definiert sind: Es muss
dann (1) für alle
x ∈ A
gelten, wobei A der Definitionsbereich von
f ist.
Manche periodische Funktionen besitzen eine kleinste Periode. (Wir nennen p
die kleinste Periode, wenn p Periode ist, aber
jede Zahl q mit
0 < q < p
keine Periode ist). Diese wird in der Regel angegeben, um periodische Funktionen zu charakterisieren
(ohne dass der Zusatz "kleinste" immer erwähnt wird). Dass nicht jede periodische
Funktion eine kleinste Periode hat, zeigt die nebenstehende Bemerkung.
| | | |
| |
| | |
Beispiele für periodische Funktionen:
|
Funktion
|
Kleinste Periode
|
|
sin x,
cos x
|
2π
|
|
tan x,
cot x,
sin2x,
cos2x
|
π
|
Sägezahnfunktion:
Im Intervall −1 ≤ x ≤ 1 wird
f (x)
= 1 − |x|
definiert, außerhalb wird f periodisch
fortgesetzt.
|
2
|
Wie das letzte Beispiel zeigt, ist es ganz leicht, durch periodische Fortsetzung viele weitere periodische
Funktionen zu definieren.
Periodizitätseigenschaften von Funktionen können ausgenutzt werden, um Berechnungen
so kurz wie möglich zu halten: Ist etwa von einer Funktion mit Periode p
eine Eigenschaft (z.B. der Verlauf ihres Graphen oder die Lage einer Nullstelle) im
Bereich 0 ≤ x < p
bekannt, so ergibt sich die entsprechende Eigenschaft für alle anderen x
ganz automatisch.
Periodische Funktionen werden benötigt, um Schwingungsvorgänge
zu modellieren, wobei dann x für die
Zeit steht und p als Periodendauer
bezeichnet wird. Eine Methode, periodische Funktionen genauer zu analysieren
(etwa um zu untersuchen, worin die Klangfarbe eines Musikinstruments physikalisch besteht),
ist die Fourieranalyse, die in einem späteren Kapitel besprochen wird.
| | | |

Fourieranalyse
| |
| | |
Stetigkeit
Wir erwähnen diesen Begriff hier nur oberflächlich, da seinen tieferen Aspekten ein eigenes
Kapitel gewidmet ist. Eine in einem Intervall A definierte Funktion
f : A → R
wird als stetig bezeichnet, wenn
kleine Änderungen von x innerhalb von
A
kleine Änderungen von f (x)
zur Folge haben. Der Graph einer stetigen Funktion ist eine zusammenhängende Kurve
(die sozusagen mit dem Bleistift nachgezogen werden kann, ohne ihn abzusetzen).
Der Begriff der Stetigkeit macht nur für Intervalle, in denen eine
Funktion definiert ist, Sinn.
Ist eine Funktion in mehreren Intervallen definiert (wie z.B.
1/x, was ja für
x = 0 nicht existiert),
so muss jeder dieser Bereiche (für 1/x
sind das die beiden Intervalle
x < 0 und
x > 0)
extra betrachtet werden. Eine unstetige Funktion ist dadurch charakterisiert, dass
die Forderung nach einem zusammenhängenden Graphen
im Definitionsbereich nicht erfüllt ist, dass also beispielsweise eine
Sprungstelle existiert (an der die Funktion definiert ist, an der der Graph aber
"auseinandergerissen" ist). Eine Funktion, die an voneinander isolierten Stellen unstetig, dazwischen
aber stetig ist, heißt stückweise (oder abschnittsweise) stetig.
Es gibt aber auch Funktionen, die auf ganz
R definiert und an jeder Stelle
unstetig sind.
Beispiele für (un)stetige Funktionen:
| | | |

Stetigkeit

Intervall
| |
| | |
|
Die Funktion
|
ist stetig...
|
und...
|
|
x2
|
in ganz R
|
|
|
|x|
|
in ganz R
|
|
|
1/x
|
in den beiden Intervallen
x < 0
und x > 0
|
ist nicht definiert für x = 0
|
|
x/(x2−1)
|
in den drei Intervallen
x < −1,
−1 < x < 1
und x > 1
|
ist nicht definiert für x = −1
und x = 1
|
|
x1/2
|
im Intervall x ≥ 0
|
ist nicht definiert für x < 0
|
|
|
in den beiden Intervallen
x < 2
und x > 2
|
ist unstetig bei x = 2
(Sprungstelle)
|
|
Dabei ist Q die Menge der rationalen Zahlen.
|
nirgends
|
ist für alle x ∈ R unstetig
|
| | | |

rationale Zahlen
| |
| | |
Nur die beiden letzten Beispiele stellen unstetige Funktionen dar, die anderen sind
(in ihren jeweiligen Definitionsbereichen) stetig.
Eine Funktion, die durch einen Term beschrieben wird, der sich durch die Grundrechnungsarten aus Potenzen,
Winkelfunktionen und deren Inversen, Exponentialfunktionen und Logarithmen aufbauen lässt, ist
in ihrem Definitionsbereich stetig. In diesem Sinn sind termdefinierte Funktionen immer stetig.
Das trifft insbesondere auf die meisten in diesem Kapitel behandelten Funktionen zu.
Weiter unten werden wir aber auch einige nützliche
unstetige Funktionen kennen lernen.
| | | |
| |
| | |
Nullstellen
Nullstellen und ihre Beziehung zu Gleichungen haben wir bereits im ersten Funktionenkapitel
kennen gelernt. Zu den einfachsten Funktionen, deren Nullstellen es sich zu untersuchen lohnt, gehören die
Polynome, auf die wir weiter unten genauer eingehen. Polynome können in der Nähe von
Nullstellen ganz verschiedenes Verhalten haben: x0
heißt Nullstelle n-ter Ordnung
der Polynomfunktion f, wenn
f (x) ≈
c (x − x0)n
für x ≈ x0 . (x − x0)n
für x ≈ x0 .
|
|
(4) |
Dabei ist n eine natürliche Zahl und
c eine von Null verschiedene Konstante.
| | | |

Nullstellen
| |
| | |
Das Verhalten von f nahe x0 ähnelt dem der Potenzfunktion
(des "Monoms")
c xn
nahe 0.
Je größer die Ordnung n ist, umso
schneller fällt der Funktionswert gegen Null, wenn sich
x der Nullstelle nähert, und
umso flacher ist der Graph in deren Nähe.
Ist n gerade, so
hat die Funktion auf beiden Seiten von x0 das gleiche Vorzeichen
(wie es für die Funktion x2 der Fall ist).
Ist n ungerade, so
sind die Vorzeichen auf beiden Seiten von x0 verschieden
(wie für die Funktion x), und der
Graph "überquert" die x-Achse. xn
nahe 0.
Je größer die Ordnung n ist, umso
schneller fällt der Funktionswert gegen Null, wenn sich
x der Nullstelle nähert, und
umso flacher ist der Graph in deren Nähe.
Ist n gerade, so
hat die Funktion auf beiden Seiten von x0 das gleiche Vorzeichen
(wie es für die Funktion x2 der Fall ist).
Ist n ungerade, so
sind die Vorzeichen auf beiden Seiten von x0 verschieden
(wie für die Funktion x), und der
Graph "überquert" die x-Achse.
Wir werden weiter unten, wenn es um Polynome geht, zeigen, dass jede Nullstelle von dieser Art ist,
d.h. eine wohldefinierte Ordnung hat.
| | | |
| |
| | |
Der Begriff der Ordung einer Nullstelle kann auf eine größere Klasse von Funktionen ausgedehnt werden.
So hat beispielsweise die Funktion
f (x)
= sin2(x)
bei jedem ganzzahligen Vielfachen von π eine Nullstelle
zweiter Ordnung. Allerdings gibt es auch Funktionen, deren Nullstellen nicht in dieses Schema
passen (Beispiel: die Betragsfunktion
f (x)
= |x| ). ).
| | | |

Ordnung von Nullstellen, allgemein
| |
| | |
Singularitäten und Pole
Ist eine reelle Funktion durch einen Term gegeben, so ist sie zunächst nicht unbedingt für
alle x ∈ R
wohldefiniert. Dabei können mehrere Dinge passieren.
- Es kann geschehen, dass ein Term an einer bestimmten Stelle nicht wohldefiniert ist,
aber durch eine nachträgliche Definition des fehlenden Funktionswerts zu einer
stetigen Funktion gemacht werden kann.
Wir sprechen dann von einer Definitionslücke, die "stetig geschlossen"
werden kann, oder einer hebbaren Singularität.
Ein Beispiel können Sie mit Hilfe des nebenstehenden Buttons aufrufen.
| | | |
| |
| | |
- Es kann aber auch geschehen, dass ein Term eine Unendlichkeitsstelle (Singularität) besitzt.
Das einfachste Beispiel ist 1/x.
Hier gibt es nichts zu rütteln − je näher
x der Zahl 0 kommt, umso
größer ist der Betrag von 1/x.
Die Stelle x = 0
gehört definitiv nicht zum Definitionsbereich (der also als
A = R \ {0}
angenommen werden kann).
Das wirft die Frage auf, wie sich eine Funktion in der Nähe einer
Unendlichkeitsstelle verhält (insbesondere "wie schnell" sie "gegen Unendlich geht").
Für rationale Funktionen, d.h. Quotienten zweier
Polynome (siehe unten), lässt sich diese Frage systematisch beantworten. Ist x0
eine Unendlichkeitsstelle der rationalen Funktion f,
so nimmt ihr Verhalten in der Nähe von x0
die Form
|
f (x) ≈
|
k
(x − x0) n
| für x ≈ x0
|
| (5) |
an, wobei n eine natürliche Zahl und
k eine von Null verschiedene Konstante
ist.
x0 wird als
Pol (Polstelle) n-ter Ordnung
bezeichnet. Um eine Idee davon zu erhalten, warum das so ist, und um zu erfahren, wie man
n und k
für eine gegebene rationale Funktion ermittelt, klicken Sie auf den nebenstehenden Button.
Das Verhalten nahe einer Polstelle wird also an den (relativ einfachen) Funktionen der Form
1/(x−x0) n gemessen.
Je größer n ist, umso rasanter wächst der
Betrag der Funktion an, wenn sich x der
Polstelle x0 nähert. Ist n gerade, so
hat die Funktion auf beiden Seiten der Polstelle das gleiche Vorzeichen
(wie es für die Funktion 1/x2 der Fall ist),
und der Graph zeigt zwei "Äste", die an der Polstelle
entweder beide nach oben oder beide nach unten "bis ins Unendliche" reichen.
Ist n ungerade, so
sind die Vorzeichen auf beiden Seiten der Polstelle verschieden
(wie für die Funktion 1/x), und der
Graph sieht zerrissen aus: ein "Ast" steigt ins "positiv Unendliche" an,
während der andere nach "negativ Unendlich" absinkt.
Die Ordnung eines Pols kann mit der Ordnung einer Nullstelle in Zusammenhang gebracht werden:
Je schneller f in der Nähe eines Pols ansteigt,
um so schneller fällt 1/f dort gegen
Null ab. Vergleichen wir (5) mit (4), so ergibt sich:
f hat bei x0 einen Pol
n-ter Ordnung, wenn
1/f dort eine Nullstelle
n-ter Ordnung besitzt.
| | | |
| |
| | |
Der Begriff des Pols kann auf eine größere Klasse von Funktionen ausgedehnt
werden. So hat beispielsweise die Tangensfunktion an der Stelle
π/2 einen Pol erster Ordnung.
- Es können auch ganz andere Dinge passieren, die sich allerdings nicht leicht
in ein einheitliches Schema bringen lassen und am Besten dann analysiert werden, wenn sie auftreten.
Ein Beispiel: 1/x + 1/|x|.
Sehen Sie sich den Graphen an, indem Sie
1/x + 1/abs(x) in den Funktions-Plotter eingeben,
und versuchen Sie, ihn auf Grund des ihn definierenden Terms zu verstehen!
(Tipp: Berechnen Sie den Funktionsterm separat für x < 0
und x > 0!)
Ein anderes Beispiel: sin(1/x) − sehen Sie sich auch deren Graphen an!
| | | |

Pol, allgemein
| |
| | |
Asymptoten und asymptotisches Verhalten
Hat der Graph einer Funktion die Tendenz, einer Geraden
immer näher zu kommen, so wird diese Asymptote genannt.
Asymptoten treten auf,
- wenn das Verhalten einer Funktion für große Werte von
x (oder −x)
dem einer linearen Funktion immer ähnlicher wird und
- bei Unendlichkeitsstellen.
Im ersten Fall sprechen wir von der asymptotischen Annäherung einer Funktion (eines Graphen)
an eine lineare Funktion (eine Gerade).
Um die Idee auszudrücken, dass über das Verhalten einer Funktion für
große, über jede Schranke wachsende Werte der unabhängigen Variable
x gesprochen wird,
werden Formulierungen wie
- "für x
→ ∞" (ausgesprochen
"für x gegen Unendlich") oder
- "für große x"
| | | |
| |
| | |
verwendet. Soll speziell über ein Verhalten für unter jede Schranke fallende Werte von
x
(d.h. über jede Schranke wachsendes −x)
gesprochen werden, so steht die Formulierung
"für x
→ −∞" (ausgesprochen
"für x gegen minus Unendlich")
zur Verfügung. Kommt es auf das Vorzeichen von x nicht
an, so wird das manchmal in der Form
"für große |x|"
oder "für |x|
→ ∞"
ausgedrückt. Daneben gibt es noch die saloppe Formulierung "im Unendlichen" oder einfach das Wort "asymptotisch".
Wie die dahinter stehenden Ideen exakter formuliert werden können, ist Gegenstand anderer
Kapitel.
| | | |

→ ∞
| |
| | |
Achtung: Der Pfeil → in einer Formulierung wie "für x
→ ∞" hat mit dem
Pfeil in den Zuordnungvorschriften für Funktionen nichts zu tun! Diese zwei Arten von Pfeilen sollten
nicht miteinander verwechselt werden!
Beispiel: Wie verhält sich die durch
f (x) =
(2x2 − 3x + 4)/x
definierte Funktion für große x?
Wir formen um und schreiben den Funktionsterm als
2x − 3 + 4/x.
Je größer x ist, umso kleiner ist der letzte
Beitrag. Daher nähert sich f (x) für
x → ∞
den Werten der linearen Funktion
g(x) =
2x − 3.
Deren Graph ist eine Gerade und stellt eine Asymptote von f dar.
Weiters hat f einen Pol bei
x = 0. Da sich der Graph dort
der y-Achse anschmiegt,
ist diese ebenfalls eine
Asymptote von f.
Um zu erfahren, wie man die Asymptoten einer gegebenen rationalen Funktion, d.h. eines Quotienten zweier
Polynome (siehe unten) systematisch bestimmt, klicken Sie auf den nebenstehenden Button.
Nicht nur rationale Funktionen können Asymptoten haben. So ist beispielsweise die durch die Gleichung
y = 2x
definierte Gerade eine Asymptote der Funktion
h(x) = 2x +
e−x,
da diese für x
→ ∞ das Verhalten der linearen Funktion
k(x) = 2x annimmt.
Die Idee des "asymptotischen Verhaltens" lässt sich
noch weiter verallgemeinern und verfeinern: So kann etwa davon gesprochen werden, dass
(2 + e−x)/x2
für große x das gleiche
asymptotische Verhalten wie 2/x2 hat,
oder dass x2 + 1/x
im Unendlichen das Verhalten von x2 annimmt.
(Benutzen Sie den Funktions-Plotter, um sich die Graphen der hier
genannten Beispiele anzusehen).
Der Sinn solcher Aussagen ist es einerseits, das "globale" Verhalten von Funktionen in den Griff
zu bekommen, und andererseits, einfache und bekannte Funktionen
als Maßstab für das Verhalten komplizierterer Funktionen zu benutzen.
| | | |

Geradengleichungen
| |
| | |
Konvexitätsverhalten
Ein bisschen salopp ausgedrückt, nennen wir eine Funktion
f : R → R
konvex (oder "nach oben offen"),
wenn jede Verbindungsstrecke zwischen zwei Punkten des Graphen von f an keiner Stelle
"unterhalb" dieses Graphen liegt.
Analog heißt eine Funktion
f : R → R
konkav ("nach unten offen"),
wenn jede Verbindungsstrecke zwischen zwei Punkten des Graphen von f an keiner Stelle
"oberhalb" dieses Graphen liegt.
Die Bezeichnungen "unterhalb" und "oberhalb" beziehen sich auf das Koordinatensystem, in dem der
Graph einer Funktion betrachtet wird: ein Punkt liegt "oberhalb" eines anderen, wenn seine
y-Koordinate größer
ist. (Achtung: in der Literatur sind die beiden Begriffe manchmal in
vertauschter Bedeutung zu finden!)
Eine Funktion ist konvex, wenn die zu ihr negative Funktion konkav ist (und umgekehrt).
Diese beiden Begriffe lassen sich auch auf Funktionen übertragen, die nicht auf ganz
R, definiert sind,
wobei sie allerdings nur einen Sinn machen, wenn sie auf ein Intervall
(d.h. einen zusammenhängenden Bereich) bezogen werden.
Eine Funktion kann in verschiedenen Intervallen ihres Definitionsbereichs
verschiedenes Konvexitätsverhalten besitzen.
- Beispiele für konvexe Funktionen: x2, x4,
x3 im Bereich x ≥ 0,
1/x im Bereich x > 0,
ex,
e−x,
|x|.
- Beispiele für konkave Funktionen: −x2,
x1/2 (in seinem Definitionsbereich
x ≥ 0),
x3 im Bereich x ≤ 0,
1/x im Bereich x < 0,
ln x (in seinem Definitionsbereich
x > 0).
| | | |
| |
| | |
Beschränktheit
Wir nennen eine Funktion
f : A → R
nach oben beschränkt, wenn es eine Zahl c
mit der Eigenschaft
gibt. c heißt dann obere Schranke.
Analog heißt f
nach unten beschränkt, wenn es eine Zahl k
mit der Eigenschaft
gibt. k heißt dann untere Schranke.
Eine Funktion, die nach oben und nach unten beschränkt ist, wird
ohne weitere Angabe als beschränkt bezeichnet (und eine Funktion, die nicht
beschränkt ist, als unbeschränkt).
Der Graph einer nach oben (unten) beschränkten Funktion liegt immer unterhalb (oberhalb) einer
zur x-Achse parallelen Geraden.
Einige Beispiele:
| | | |
| |
| | |
- Nach oben beschränkt:
−x2,
1 − x4.
- Nach unten beschränkt: x2,
x4 − 3,
ex,
|x|.
- Nach oben und unten beschränkt:
1/(x2 + 1),
sin x,
cos x.

|
Wir werden diesen Begriff in einem späteren Kapitel wieder aufnehmen und beispielsweise fragen, wann es
eine kleinste obere und eine größte untere Schranke gibt.
| | | |
| |
| | |
Funktionen kombinieren
Es gibt zahlreiche Möglichkeiten, Funktionen miteinander zu kombinieren:
- Summe, Differenz, Produkt, Quotient:
Was bedeutet es eigentlich, "zwei Funktionen zu addieren"?
Ist A ⊆ R
und sind
f : A → R
und
g : A → R
zwei reelle Funktionen mit (dem selben) Definitionsbereich A, so kann aus ihnen eine dritte Funktion
f + g : A → R
(ebenfalls mit Definitionsbereich A) durch
|
(f + g) (x)
= f (x)
+ g (x)
für alle x ∈ A
|
|
(8) |
definiert werden. Man sagt, dass die Summe zweier Funktionen punktweise
(d.h. für jeden "Punkt" x als
Summe der Funktionswerte von f und g) definiert ist.
In völlig analoger Weise kann die Differenz und das Produkt zweier Funktionen definiert werden.
Auf diese Weise wird die Menge aller Funktionen
A → R
mit den "Rechenoperationen" Plus, Minus und Mal ausgestattet. Daher kann etwa auch
das Quadrat f 2 einer
Funktion f gebildet werden.
(In diesem Sinn ist ja auch üblich, sin2x
für (sin x)2 zu schreiben).
Beim Quotienten müssen wir ein bisschen
aufpassen, da wir ja nicht durch Null dividieren dürfen. Er kann punktweise als Funktion
f/g : B → R
definiert werden, wobei
B = {
x ∈ A |
g(x)
≠ 0 }
ist.
- Verkettung (Hintereinander-Ausführen): Welche Struktur hat die durch den
Term sin(x2) definierte Funktion?
Sie wird auf ein x angewandt, indem
zuerst auf x die Funktion "Quadrieren" und
danach auf das Resultat
(also x2) die Funktion "Sinus" angewandt wird.
Analoges lässt sich auch mit anderen Funktionen machen:
Wird erst die Funktion g auf
x angewandt und danach
auf das Resultat die Funktion f, so
erhalten wir f (g(x)).
Die Funktion, die diese beiden Schritte kombiniert, heißt Verkettung
(manchmal auch Verknüpfung)
von f und g
und wird mit f o g bezeichnet:
Dabei muss der Wertebereich von g eine
Teilmenge des Definitionsbereichs von f
sein, da es ansonsten ein x gibt,
für das zwar g(x),
nicht aber
f (g(x))
nicht definiert ist.
Innerhalb der Menge aller Funktionen R → R
darf beliebig verkettet werden. Die Verkettung ist eine "Operation", die, ähnlich wie die
Multiplikation, aus zwei Funktionen eine dritte macht, und wie die Multiplikation erfüllt sie das
so genannte "Assoziativgesetz"
|
f o (g o h)
=
(f o g) o h .
|
|
(10) |
Allerdings kommt es bei ihr auf die Reihenfolge an. f o g ist nicht dasselbe wie
g o f.
(Beispiel: sin2(x)
ist nicht dasselbe wie sin(x2)).
In der mathematischen Fachsprache heißt das:
Die Verkettung ist nicht "kommutativ".
Die Reihenfolge, in der die beiden Funktionen angewandt werden, läuft übrigens ein bisschen gegen unsere
Intuition: Trotz der Bezeichnung "f o g" wird zuerst g
und danach f angewandt. (Die
Gefahr, die Reihenfolge zu verwechseln, rührt daher, dass in der üblichen Schreibweise
"f (x)"
das Funktionssymbol f links von
x steht, in diesem Sinn also
Funktionen "von links" wirken).
Stellen wir die Wirkung einer Funktion f auf ein
Element x in der Form
dar, so kommt die Verkettung f o g so zustande:
In formaler Hinsicht lassen sich "Potenzen" von Verkettungen wie f o f definieren. Letzteres darf aber nicht
mit dem punktweise definierten Quadrat einer Funktion verwechselt werden:
Ist etwa f die Sinusfunktion, so ist
(f o f )(x)
= sin(sin(x)), während
f 2(x)
= sin2x ist.
| | | |

kommutativ
| |
| | |
Das alles ist wichtig, weil sich Funktionen, die durch längere Terme
dargestellt werden, als Verkettungen einfacherer Funktionen auffassen lassen.
Manche mathematischen Eigenschaften von Funktionen
lassen sich auf entsprechende Eigenschaften der Bestandteile zurückführen, wodurch
sich oft umständliche Rechnungen vermeiden lassen.
(Ein berühmtes Beispiel ist die in der Differentialrechnung auftretende "Kettenregel").
- Verschiebungen und Streckungen:
Nehmen Sie an, Sie haben die Eigenschaften einer Funktion f
anhand ihres Graphen studiert und kennen sie jetzt recht gut.
Dann bekommen Sie eine andere Funktion g vorgesetzt, die durch
g(x) =
f (x − 2)
definiert ist (also der Verkettung von f
mit der linearen Funktion
h(x)
= x − 2).
Können Sie auf Anhieb sagen, wie der Graph von g
aussieht? Die Antwort ist: Der Graph von g
geht aus dem Graphen von f hervor, indem
er um 2 nach "rechts" (in x-Richtung)
verschoben wird.
Wir fassen hier einige derartige Situationen zusammen:
|
Der Graph der Funktion
|
geht aus jenem von f hervor durch
|
|
g(x) =
f (x) + c
|
Verschiebung um c in y-Richtung.
|
|
g(x) =
f (x − c)
|
Verschiebung um c in x-Richtung.
|
|
g(x) =
k f (x)
|
Streckung um den Faktor k in y-Richtung.
Falls k < 0: zusätzlich Spiegelung
an der x-Achse.
|
|
g(x) =
f (x/k)
|
Streckung um den Faktor k in x-Richtung.
Falls k < 0: zusätzlich Spiegelung
an der y-Achse.
|
Ist c < 0, so ist die angegebene Verschiebung
in die negative x- bzw.
y-Richtung durchzuführen.
In den letzten beiden Fällen
muss k ≠ 0
sein. Ist |k| < 1, so handelt es
sich bei der angegebenen "Streckung" und eine "Stauchung".
Der Graph einer Funktion der Form
g(x) =
a f (x/k − c)
+ b
wird aus jenem von f durch eine entsprechende Kombination von
Verschiebungen und Streckungen gewonnen. Daraus folgt beispielsweise, dass die
Graphen aller Funktionen der Form
g(x) =
a (x − c)2
+ b
(solange a ≠ 0 ist)
Parabeln sind.
Diese Formeln erleichtern es oft, Eigenschaften neu auftretender Funktionen auf
Bekanntes zurückzuführen.
| | | |

Kettenregel
| |
| | |
Inverse Funktion (Umkehrfunktion)
Der Begriff der zu einer gegebenen Funktion inverse Funktion (Umkehrfunktion) wurde bereits
im ersten Funktionenkapitel eingeführt. Wir wollen ihn hier von der formalen
Seite her ein bisschen genauer diskutieren.
Ausgangpunkt ist eine bijektive
(invertierbare, umkehrbare) Funktion
f : A → B.
Dabei sind A und B
beliebige Mengen. Die Forderung der Bijektivität bedeutet: Jedes Element von
B tritt genau einmal
als Funktionswert eines Elements von A auf.
In Formeln: für jedes
y ∈ B
existiert genau ein
x ∈ A,
für das
y =
f (x)
gilt. Die Zuordnungsvorschrift kann daher "umgedreht werden":
Jedem y ∈ B
kann genau jenes eindeutig bestimmte x ∈ A
zugeordnet werden, für das y =
f (x) gilt.
Diese umgekehrte Zuordnung definiert die zu f inverse Funktion (Umkehrfunktion oder einfach Inverse)
f −1 : B → A .
(Achtung: f −1(x) ist
nicht zu verwechseln mit
f (x)−1
≡ 1/f (x);
hier ist die Notation leider nicht konsistent).
Wird die durch f
definierte funktionale Abhängigkeit in der Form y =
y(x)
geschrieben ("y als Funktion von x"),
so entspricht die inverse Funktion der Abhängigkeit
x =
x(y)
("x als Funktion von y").
Der Graph von f −1
geht aus dem Graphen von f
durch Spiegelung an der ersten Mediane (d.h. an der Geraden mit der
Gleichung y = x),
mit anderen Worten durch Vertauschen der von den Koordinaten x
und y gespielten Rollen hervor.
Die Inverse einer bijektiven Funktion ist klarerweise wieder bijektiv. Wird die Inverse der Inversen gebildet, kommt wieder die ursprüngliche
Funktion heraus. In Formeln können wir das als
(f −1)−1 = f
anschreiben.
Die Tatsache, dass die Inverse einer Funktion aus der Umkehrung der Zuordnung hervorgeht, kann auch
in der Form
|
f −1(f (x))
= x
für alle x ∈ A
|
|
(13) |
oder in der Form
|
f (f −1(y))
= y
für alle y ∈ B
|
|
(14) |
ausgedrückt werden. Verwenden wir die Bezeichnung für die Verkettung von Funktionen (s.o.)
und benutzen das Symbol idM
für die identische Funktion auf der Menge M
|
idM(x)
= x
für alle
x ∈ M,
|
|
(15) |
so können die Formeln (13) und (14) als
|
f −1 o f = idA
und
f o f −1
= idB
|
|
(16) |
geschrieben werden. Die zu einer Funktion f Inverse ist also jene
Funktion, die unter Verkettung mit f die identische
Funktion ergibt. Hier haben wir den tieferen Grund dafür, warum wir die inverse Funktion
mit dem Symbol f −1
bezeichnen: Wird die Verkettung o als eine Art (nicht-kommutativer) Multiplikation
von Funktionen und die identische Funktion als die "Eins" aufgefasst,
so erinnert (16) an die Formel
a−1a = 1
für reelle Zahlen.
Im Rahmen des an der Vanderbilt University zur Verfügung gestellten
MathServ Project
finden Sie das auf Mathematica beruhende
und für paktische Rechnungen nützliche Online-Werkzeug
Inverse Funktion berechnen.
| | | |

inverse Funktion
| |
| | |
Explizite und implizite Funktionsdarstellung
Oft werden Funktionen durch Terme definiert (man spricht dann von termdefinierten Funktionen)
− manchmal auch durch mehrere Terme, die
mittels einer Fallunterscheidung kombiniert werden
(diese heißen abschnittsweise oder stückweise termdefinierte Funktionen).
In allen Fällen, in denen Funktionswerte durch die direkte Auswertung eines Ausdrucks berechnet
werden können, liegt eine explizite Funktionsdarstellung vor.
Sehen wir uns ein Beispiel an: Durch die Gleichung
wird unmittelbar ausgedrückt, wie die Größe y
von der Größe x abhängt.
Wir können diese Abhängigkeit als Funktion in der Form
y(x) =
x2 − 3
anschreiben. Daher wird eine Gleichung wie (17) auch (explizite) Funktionsgleichung genannt.
Funktionale Zusammenhänge liegen aber manchmal weniger offen zu Tage.
Betrachten wir etwa die Gleichung
Sie stellt ebenfalls eine Art von Funktionsgleichung dar: Die beiden Größen
x und y
hängen voneinander ab. Wir interessieren uns nun wieder dafür, "wie y von
x abhängt". Im Unterschied zu (17)
ist die Variable y aber hier noch nicht
"freigelegt" − wir sprechen von einer impliziten Funktionsdarstellung
(oder impliziten Funktionsdefinition), und eine Gleichung wie (18) wird auch implizite Funktionsgleichung genannt.
Dabei kann allerhand passieren, wie unser Beispiel zeigt:
Lösen wir (18) nach y
auf, so erhalten wir − wie es für quadratische Gleichungen nicht ungewöhnlich ist −
gleich zwei Lösungen. Dementsprechend stecken in Gleichung (18) zwei Funktionen:
y±(x) =
−1 ± (1 − x2)1/2.
Zudem kann x nicht beliebig vorgegeben werden, denn
aufgrund der Wurzelfunktion, die hier auftritt, sind beide Funktionen
(im Rahmen der reellen Zahlen) nur für |x| ≤ 1
definiert.
| | | |

quadratische
Gleichungen
| |
| | |
Ist eine Funktion in impliziter Form gegeben, so kann dies also
(im Vergleich zur expliziten Form) die Notwendigkeit einer zusätzlichen Analyse nach sich ziehen,
damit überhaupt klar gesagt werden kann, was gemeint ist.
Dennoch ist diese Form der Darstellung nicht unwichtig, da viele Zusammenhänge (auch in Anwendungsbereichen)
zunächst implizit in Erscheinung treten. Manchmal ist es auch ganz einfach bequemer, eine bestimmte
Funktion in impliziter statt in expliziter Form anzugeben.
Funktionen ohne geschlossene Termdarstellung
Wir haben im vorigen Unter-Abschnitt gesehen, dass implizite Funktionsdarstellungen
Probleme bereiten können: Um überhaupt klar sagen zu können, welche Funktionen durch Gleichung (18)
definiert sind, war es nötig, eine Gleichung zu lösen.
Immerhin sind wir mit zwei schönen Termen belohnt worden. Es geht aber noch schlimmer:
Als Johannes Kepler um das Jahr 1619 an seinem dritten Gesetz über den Umlauf der Planeten um die Sonne
arbeitete, stieß er auf die Gleichung
2 y
− sin y
= x. y
− sin y
= x.
|
|
(19) |
(In Wahrheit stand an Stelle der 2 eine beliebige Konstante ≥ 1, aber wir wollen es
bei dieser Form belassen). Durch sie ist eine Funktion y(x) bestimmt.
Im Gegensatz zu (18) ist es hier tatsächlich nur eine: Wenn Sie die Funktion
x(y)
= 2 y
− sin y plotten, sehen Sie, dass es zu jedem x genau ein y gibt.
(Wenn Sie den Funktions-Plotter dazu benutzen,
müssen Sie zuvor die Variable y auf den Namen x
umtaufen). Von dieser Funktion kann man nun beweisen (was wir hier allerdings nicht tun), dass sie sich
nicht in "geschlossener Form", d.h. mit Hilfe eines Term,
der aus den uns bisher bekannten Rechenoperationen und Funktionen aufgebaut ist,
darstellen lässt! Das bedeutet nicht, dass wir sie nicht ebenso untersuchen
können wie andere Funktionen auch.
Wir können von ihr zum Beispiel sagen, dass sie die Umkehrfunktion von
x(y)
= 2 y
− sin y ist, dass sie genau eine Nullstelle besitzt, und zwar bei
x = 0,
dass sie streng monoton wachsend ist, und dass
y(2π) = 4π
gilt. Aber durch das Fehlen einer geschlossenen Darstellung ist es ein bisschen mühsam,
diese Informationen zu erlangen. y
− sin y ist, dass sie genau eine Nullstelle besitzt, und zwar bei
x = 0,
dass sie streng monoton wachsend ist, und dass
y(2π) = 4π
gilt. Aber durch das Fehlen einer geschlossenen Darstellung ist es ein bisschen mühsam,
diese Informationen zu erlangen.
Ähnliches gilt für viele andere Funktionen, die mathematische Relevanz besitzen,
und die großteils mit Hilfe weiterer Methoden definiert sind
(beispielsweise als Potenzreihe ("Polynom unendlichen Grades"),
als Integral
oder als Lösung einer Differentialgleichung).
Ein berühmtes Beispiel ist der Umfang der Ellipse, der sich nicht geschlossen
durch die Längen der Halbachsen ausdrücken lässt.
Manche dieser Funktionen haben eigene Namen bekommen
(wie wir das ja auch, wie Sie sich vielleicht erinnern, mit den Winkelfunktionen gemacht haben,
indem wir zwei neu aufgetretene Funktionen auf die Namen Sinus und Cosinus getauft haben).
Viele Bezeichnungen wie "Besselfunktionen", "Gaußsche Fehlerfunktion" oder "Riemannsche Zetafunktion"
sind auf diese Weise entstanden.
| | | |

Potenzreihe
Ellipsenumfang
(in Vorbereitung)
Differentialgleichung
(in Vorbereitung)
Winkelfunktionen
| |
| | |
Familien von Funktionen
Manchmal möchte man eine größere Menge von Funktionen auf einen Satz
betrachten. Beispielsweise ist durch
für jedes reelle t eine
Funktion ft
definiert. Die Menge aller ft
ist eine Familie (oder Schar) von Funktionen, und
die Größe t heißt
Parameter der Familie. Sie hat einen anderen logischen Status als die
unabhängige Variable x.
Ein bisschen salopp könnte man sagen, dass sie die Funktionen der Familie
"durchnummeriert". Überlegen Sie, wie die Graphen der Funktionen dieser Familie
aussehen und was sie gemeinsam haben!
Manchmal ist es günstig, sich den Parameter t
als Zeit vorzustellen. Die obige Familie wird dann zu einem "Film", in dem
zu jedem Zeitpunkt eine andere Funktion vorliegt. Überlegen Sie, wie dieser
Film aussieht, wenn sie die Graphen der Funktionen betrachten!
Um einen solchen "Film" anzusehen, können Sie unseren
Excel-Plotter
verwenden. (Parameter müssen in diesem Werkzeug die Namen a, b,
c, d oder k tragen).
Geben Sie den Term (20) ein, wobei Sie t
durch a ersetzen, d.h.
(x-a)^2-a^2,
und variieren Sie a!
Ein zweites Beispiel: Für jedes a ≥ 1 definiert die
so genannte "Kepler-Gleichung"
a y
− sin y
= x
eine Funktion ya(x).
Hier spielt a die Rolle eines Parameters.
Wir haben sie oben in (19) für den Spezialfall
a = 2 betrachtet. y
− sin y
= x
eine Funktion ya(x).
Hier spielt a die Rolle eines Parameters.
Wir haben sie oben in (19) für den Spezialfall
a = 2 betrachtet.
Ganz allgemein sind die "Konstanten", die so oft in Funktionstermen vorkommen,
Parameter, da ein solcher Term nicht eine Funktion,
sondern eine ganze Familie von Funktionen definiert.
| | | |

ein weiteres Beispiel
| |
| | |
Algebraische und transzendente Funktionen
Zwei Begriffe zum Thema Funktionen werden Sie ab und zu in mathematischen Texten finden:
- Eine reelle Funktion f heißt algebraisch, wenn sie eine "polynomische
Gleichung" (also beispielsweise eine Gleichung der Form
f 3(x)
− 3x7 f (x)
+ x4
= 0)
identisch (d.h. für alle x
aus ihrem Definitionsbereich) erfüllt.
Jeder Term, der sich aus x
durch die Grundrechnungsarten und das Bilden von Potenzen mit rationalen Exponenten
aufbauen lässt, stellt eine algebraische Funktion dar. Beispiele sind
Polynome, rationale Funktionen, Wurzelfunktionen und beliebige Kombinationen
(auch Verkettungen) dieser.
- Neben den algebraischen bilden die transzendenten Funktionen eine wichtige Klasse.
Wir wollen diesen Begriff hier nicht genau definieren, sondern erwähnen lediglich,
dass alle termdefinierten Funktionen, die sich nicht allein durch die
Grundrechnungsarten und das Bilden von Potenzen mit rationalen Exponenten
aufbauen lassen (z.B. weil sie Winkelfunktionen oder deren Inverse,
Exponentialfunktionen oder Logarithmen enthalten), transzendent sind.
| | | |
| |
| | |
Ausblicke
Wir werden in späteren Kapiteln weitere fundamentale Konzepte zum Studium und
zur Anwendung von Funktionen kennen lernen.
Da der Funktionsbegriff praktisch überall eine Rolle spielt,
zählen wir hier nur die wichtigsten auf:
- Der bereits oben oberflächlich gestreifte Begriff der Stetigkeit
von Funktionen wird auf eine solidere Basis gestellt werden.
- Im Rahmen der Differentialrechnung wird ein zentrales
Thema der modernen Mathematik eingeführt: die Begriffe der Ableitung und der Differenzierbarkeit einer Funktion.
Sie werden es unter anderem erlauben, die Steigung von Funktionsgraphen zu
berechnen und Minima und Maxima von Funktionen zu ermitteln.
- Das Studium von Potenzreihen, "Polynomen mit unendlich vielen Termen",
wird neue Gesichtspunkte zum Funktionsbegriff und Näherungsverfahren zu Funktionsberechnungen ergeben.
- Die Theorie der Fourierreihen wird es ermöglichen, die in einer
periodischen Funktion steckenden Frequenzen herauszufiltern.
- Schließlich wird die Einbeziehung komplexer Zahlen
verborgene Zusammenhänge zwischen Winkelfunktionen und Exponentialfunktionen aufdecken.
|
| | |

Stetigkeit
∗
Ableitung und Differenzierbarkeit
∗
Potenzreihen
∗
Fourierreihen
∗
komplexe Zahlen
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
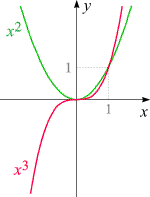
Potenzfunktionen sind Funktionen der Form
x →
xm
oder, etwas allgemeiner,
x →
c xm.
Im ersten Funktionenkapitel haben wir sie für den Fall besprochen, dass der Exponent
m eine (positive oder negative)
ganze Zahl ist (Beispiel: x xm.
Im ersten Funktionenkapitel haben wir sie für den Fall besprochen, dass der Exponent
m eine (positive oder negative)
ganze Zahl ist (Beispiel: x −3 = 1/x3).
Aus diesem Kapitel übernehmen wir die beiden Zusammenstellungen
Hier eine Zusammenstellung weiterer wichtiger Eigenschaften dieser Funktionen und Beispiele für ihre Graphen: −3 = 1/x3).
Aus diesem Kapitel übernehmen wir die beiden Zusammenstellungen
Hier eine Zusammenstellung weiterer wichtiger Eigenschaften dieser Funktionen und Beispiele für ihre Graphen:
|
Steckbrief der Funktionen
x –→
xm
für natürliches m
(m = 1, 2, 3, ...)
|
- Definitionsbereich: R
- Wertebereich:
für gerades m: R0+;
für ungerades m: R
- Injektivität:
für gerades m: nicht injektiv;
für ungerades m: injektiv
- Monotonie:
für gerades m: nicht monoton;
für ungerades m: streng monoton wachsend
- Periodizität: keine
- Positivität:
für gerades m: überall ≥ 0
- Nullstellen: bei x = 0 Nullstelle
m-ter Ordnung
- Asymptoten: keine
- Unendlichkeitsstellen: keine
|
|
|
|
Steckbrief der Funktionen
x –→
xm
für negatives ganzzahliges m
(m = −1, −2, −3, ...)
|
- Definitionsbereich: R \ {0}
- Wertebereich:
für gerades m: R+;
für ungerades m: R \ {0}
- Injektivität:
für gerades m: nicht injektiv;
für ungerades m: injektiv
- Monotonie:
für gerades m:
im Bereich x < 0 streng monoton wachsend,
im Bereich x > 0 streng monoton fallend;
für ungerades m:
in den Bereichen x < 0
und x > 0 streng monoton fallend
- Periodizität: keine
- Positivität:
für gerades m: überall > 0
- Nullstellen: keine
- Asymptoten: beide Koordinatenachsen
- Unendlichkeitsstellen: Pol |m|-ter Ordnung
bei x = 0
|
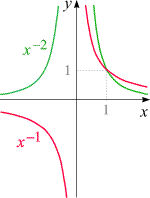
|
|
| | | |

Potenzfunktionen
mit ganzzahligen Exponenten
| |
| | |
Mit Hilfe der zwei nebenstehenden Puzzle-Applets können Sie
die Zuordnung von Funktionsstermen, die Potenzfunktionen
mit ganzzahligen Exponenten enthalten, zu ihren Graphen üben.
Weiters haben wir bereits früher den Begriff der Potenz
für rationale Exponenten m ausgedehnt.
Der wichtigste Spezialfall ist m = 1/2, in dem sich die
Wurzelfunktion ergibt:
Schließlich haben wir den allgemeinen Fall, in dem beliebige
reelle Zahlen als Exponenten zugelassen sind, konstruiert. Hier
die Steckbriefe dieser Funktionen:
|
Steckbrief der Funktionen
x –→
xm
für positives reelles nicht-ganzzahliges m
|
- Definitionsbereich: R0+
- Wertebereich: R0+
- Injektivität: injektiv
- Monotonie: streng monoton wachsend
- Periodizität: keine
- Positivität: überall ≥ 0
- Nullstellen: x = 0
- Asymptoten: keine
- Unendlichkeitsstellen: keine
|
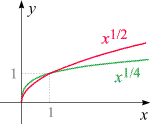
|
|
|
Steckbrief der Funktionen
x –→
xm
für negatives reelles nicht-ganzzahliges m
|
- Definitionsbereich: R+
- Wertebereich: R+
- Injektivität: injektiv
- Monotonie: streng monoton fallend
- Periodizität: keine
- Positivität: überall > 0
- Nullstellen: keine
- Asymptoten: keine
- Unendlichkeitsstellen: bei x = 0
|
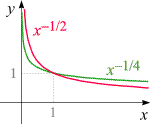
|
|
|
| | |
Applets
Funktionen
erkennen 2
und
Graphen
erkennen 2

Potenzen mit rationalen
und reellen
Exponenten
| |
| | |
| Polynome und rationale Funktionen |
| | | |
Zum Seitenanfang | |
| | |
Eine Polynomfunktionen (der Ordnung m) ist eine Funktion der Form
|
p(x) =
am
xm
+ am−1
xm−1
+ ... +
a1
x + a0 .
|
|
(22) |
Wir haben Polynome in einem früheren Kapitel eingeführt, und im ersten Funktionenkapitel haben wir einfache Polynomfunktionen (bis zur zweiten Ordnung)
besprochen. Polynomfunktionen werden manchmal auch "ganzrationale Funktionen" genannt.
| | | |

Polynome

Polynomfunktionen
| |
| | |
Polynome sie genau jene Terme, die sich aus einer Variablen und einem endlichen Satz reeller Zahlen
durch Addition, Subtraktion und Muliplikation aufbauen lassen. In diesem Sinn zählen sie
zu den elementarsten mathematischen Objekten, und es ist wenig Vorwissen nötig, um zu verstehen, was ein Polynom ist.
Andererseits decken sie ein breites Verhaltensspektrum ab, und mit ihnen sind tiefe mathematische Resultate verbunden.
Dass Polynome verschiedene Arten von Nullstellen (Nullstellen verschiedener Ordnung) haben können,
wurde bereits oben behandelt.
Im nebenstehenden Exkurs können Sie einige wissenswerte Informationen
über Polynomfunktionen und ihre Graphen aufrufen. Unter anderem erfahren Sie,
- dass jede Nullstelle x0
eines Polynoms p eine wohldefinierte Ordnung
besitzt, da sie zu einer "Abspaltung"
führt, wobei n die Ordnung (oder Vielfachheit) der
Nullstelle und h ein
Polynom mit h(x0) ≠ 0
ist,
- wie dies (manchmal) benutzt werden kann, um die Nullstellen eines Polynoms zu bestimmen, und
- wie die Ordnung eines Polynoms mit der Form seines Graphen zusammenhängt.
Eine rationale Funktion ist ein Quotient zweier Polynome.
Rationale Funktionen entsprechen genau jenen Termen, die sich aus einer Variablen und einem endlichen Satz reeller Zahlen
durch die Grundrechnungsarten (Addition, Subtraktion, Muliplikation und Division) aufbauen lassen.
Zahlreiche in Anwendungsbereichen auftretende Funktionen und "Formeln" sind von
einer solchen Form. Darüber hinaus bieten rationale Funktionen gute und nicht allzu schwierige Gelegenheiten,
mit fundamentalen Konzepten zu operieren. Hier eine mögliche Checkliste bei der Untersuchung einer gegebenen
rationalen Funktion f auf Nullstellen, Pole und Asymptoten:
| | | |
| |
| | |
- Untersuchen, ob eine Definitionslücke vorliegt, wie es oben anhand eines Beispiels gezeigt
wurde. Ist f als Quotient zweier Polynome gegeben, so sind alle Definitionslücken
behoben, wenn maximal gekürzt wurde. Danach liegt die Funktion in Form eine Terms
p(x)/q(x)
vor, bei dem Zähler p und Nenner q
Polynome sind, die keine gemeinsamen Nullstellen mehr besitzen. Für die folgenden Punkte ist diese gekürzte Version zu verwenden.
Ist der Nenner q
zumindest von erster Ordnung, so heißt f
auch "gebrochen rationale Funktion".
- Checken, ob f Nullstellen besitzt.
Die Nullstellen von f sind jene des Zählers
p.
- Checken, of f Pole besitzt.
Die Polstellen von f sind die Nullstellen des Nenners q.
Wir haben oben besprochen, wie auch deren Ordnungen gefunden werden können.
- Checken, ob f Asymptoten besitzt. Wie sie ermittelt werden,
haben wir ebenfalls oben behandelt.
| | | |
| |
| | |
Später, im Rahmen der Differentialrechnung, werden wir weitere Methoden zur Funktionsuntersuchung
("Kurvendiskussionen") kennen lernen,
die sich auch auf Polynome und rationale Funktionen anwenden lassen.
|
| | |

Kurvendiskussionen
| |
| | |
| Winkelfunktionen und ihre Inversen |
| | | |
Zum Seitenanfang | |
| | |
Winkelfunktionen wurden in einem eigenen Kapitel eingeführt und viele ihrer Eigenschaften
ausführlich besprochen. So sehen ihre Graphen und die ihrer Inversen aus:
Die Winkelfunktionen wurden anhand geometrischer Situationen definiert, und diese Definitionen lassen sich
auch verwenden, um ihre Graphen zu verstehen. Das können Sie mit Hilfe des nebenstehenden
interaktiven Applets selbst nachvollziehen.
Hier die Steckbriefe der Sinus- und Cosinusfunktion:
| | | |

Winkelfunktionen
Applet
Die Graphen von
sin, cos und tan
| |
| | |
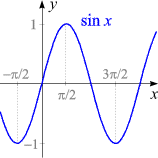
|
Steckbrief der Funktion
x –→
sin x
|
- Definitionsbereich: R
- Wertebereich: das Invervall −1 ≤ x ≤ 1
- Injektivität: nicht injektiv
- Monotonie:
im Bereich
−π/2 ≤ x ≤ π/2
streng monoton wachsend;
im Bereich π/2 ≤ x ≤ 3π/2 streng monoton fallend;
Monotonie-Bereiche wiederholen sich periodisch
- Periodizität: kleinste Periode = 2π
- Positivität:
im Bereich
0 < x < π
positiv;
im Bereich π < x < 2π negativ;
Bereiche wiederholen sich periodisch
- Nullstellen: bei jedem ganzzahligen Vielfachen von π
Nullstelle erster Ordnung
- Asymptoten: keine
- Unendlichkeitsstellen: keine
|
|
|
|
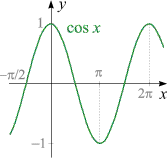
Steckbrief der Funktion
x –→
cos x
|
- Definitionsbereich: R
- Wertebereich: das Invervall −1 ≤ x ≤ 1
- Injektivität: nicht injektiv
- Monotonie:
im Bereich
0 ≤ x ≤ π
streng monoton fallend;
im Bereich π ≤ x ≤ 2π streng monoton wachsend;
Monotonie-Bereiche wiederholen sich periodisch
- Periodizität: kleinste Periode = 2π
- Positivität:
im Bereich
−π/2 < x < π/2
positiv;
im Bereich π/2 < x < 3π/2 negativ;
Bereiche wiederholen sich periodisch
- Nullstellen: bei jedem (n + 1/2)π
mit ganzzahligem n Nullstelle erster Ordnung
- Asymptoten: keine
- Unendlichkeitsstellen: keine
|
|
|
Sie werden unter anderem dazu verwendet, um Schwingungsvorgänge zu modellieren. Ist t die Zeit, so stellt
s(t) = A sin(ωt + δ)
eine "harmonische Schwingung" ("Sinusschwingung") mit Amplitude A
und Kreisfrequenz ω dar.
Die Frequenz ν ist durch
ω = 2πν gegeben,
die Periodendauer beträgt
T = 1/ν = 2π/ω.
Der Term
ωt + δ
wird Phase genannt.
Die Konstante δ stellt eine Zeitverschiebung gegenüber
sin(ωt) dar
und wird als Anfangsphase oder Phasenverschiebung bezeichnet. Mit Hilfe der zwei nebenstehenden Puzzle-Applets können Sie
die Zuordnung solcher Terme mit verschiedenen Amplituden, Frequenzen und Anfangsphasen zu ihren Graphen üben.
| | | |
Applets
Funktionen
erkennen 3
und
Graphen
erkennen 3
| |
| | |
Aus den Eigenschaften der Sinus- und der Cosunusfunktion ergeben sich jene ihres Quotienten, der durch
tan x = sin x/cos x definierten
Tangensfunktion:
|
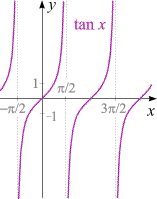
Steckbrief der Funktion
x –→
tan x
|
- Definitionsbereich: R \
{ (n + 1/2)π |
n ganzzahlig }
- Wertebereich: R
- Injektivität: nicht injektiv
- Monotonie:
im Bereich
−π/2 < x < π/2
streng monoton wachsend;
Monotonie-Bereiche wiederholen sich periodisch
- Periodizität: kleinste Periode = π
- Positivität:
im Bereich
−π/2 < x < 0
negativ;
im Bereich 0 < x < π/2 positiv;
Bereiche wiederholen sich periodisch
- Nullstellen: bei jedem ganzzahligen Vielfachen von π
Nullstelle erster Ordnung
- Asymptoten: die Geraden x = (n + 1/2)π
mit ganzzahligem n
- Unendlichkeitsstellen: Pole erster Ordnung an allen Stellen (n + 1/2)π
mit ganzzahligem n
|
|
|
Die Cotangensfunktion (cot x = 1/tan x)
ist dank der leicht zu beweisenden Beziehung
cot x = − tan(x − π/2)
lediglich eine "gespiegelte" und "verschobene" Variante der Tangensfunktion.
(Das ist ein schönes Anwendungsbeispiel für die oben besprochene
Auswirkung einer Verschiebung im Argument). tan(x − π/2)
lediglich eine "gespiegelte" und "verschobene" Variante der Tangensfunktion.
(Das ist ein schönes Anwendungsbeispiel für die oben besprochene
Auswirkung einer Verschiebung im Argument).
Die Graphen der inversen Winkelfunktionen sind Teilstücke jener Kurven, die durch
Spiegelungen der entsprechenden Winkelfunktions-Graphen an der ersten Mediane (s.o.)
entstehen. Die interessanteste ist der Arcus Tangens:
| | | |

inverse
Winkelfunktionen
| |
| | |
|
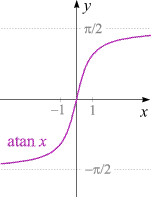
Steckbrief der Funktion
x –→
atan x
|
- Definitionsbereich: R
- Wertebereich: das Intervall −π/2 < x < π/2
- Injektivität: injektiv
- Monotonie: streng monoton steigend
- Periodizität: keine
- Positivität:
im Bereich x < 0
negativ;
im Bereich x > 0 positiv
- Nullstellen: bei x = 0
Nullstelle erster Ordnung
- Asymptoten: die Geraden
y = ±π/2
- Unendlichkeitsstellen: keine
|
|
|
Diese Funktion bildet die Menge der reellen Zahlen bijektiv auf das offene Intervall
−π/2 < x < π/2,
das wir auch als (−π/2, π/2) schreiben können, ab
und beweist somit, dass dieses zur gesamten
Menge R gleichmächtig ist
(d.h. "gleich viele" Elemente enthält).
|
| | |

offene Intervalle

gleichmächtig
| |
| | |
| Exponential- und Logarithmusfunktionen |
| | | |
Zum Seitenanfang | |
| | |
Exponentialfunktionen wurden bereits in einem früheren Kapitel eingeführt. Wir haben dort auch
ihre Graphen, die den Ablauf von Wachstums- und Zerfallsprozessen darstellen, und ihre Inversen,
die Logarithmusfunktionen, kennen gelernt.
Hier noch einmal die Graphen im Überblick
und die Steckbriefe der beiden auf die natürliche Basis e bezogenen
Funktionen:
|
Steckbrief der Funktion
x –→
exp x
|
- Definitionsbereich: R
- Wertebereich: R+
- Injektivität: injektiv
- Monotonie: streng monoton wachsend
- Periodizität: keine
- Positivität: überall > 0
- Nullstellen: keine
- Asymptoten: x-Achse
- Unendlichkeitsstellen: keine
|
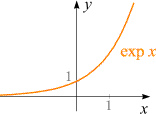
|
|
|
Steckbrief der Funktion
x –→
ln x
|
- Definitionsbereich: R+
- Wertebereich: R
- Injektivität: injektiv
- Monotonie: streng monoton wachsend
- Periodizität: keine
- Positivität: im Bereich 0 < x < 1
negativ; im Bereich x > 1 positiv
- Nullstellen: bei x = 1
Nullstelle erster Ordnung
- Asymptoten: y-Achse
- Unendlichkeitsstellen: bei x = 0
|
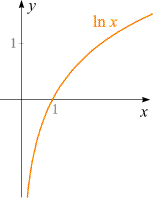
|
|
| | | |

Exponentialfkt.
und Logarithmus
| |
| | |
Hyperbelfunktionen
Mit Hilfe der Exponentialfunktion zur Basis e werden die so genannten Hyperbelfunktionen
(Sinus Hyperbolicus, Cosinus Hyperbolicus, Tangens Hyperbolicus und Cotangens Hyperbolicus)
definiert:
Nicht nur die Namen erinnern an die Winkelfunktionen − auch
(26) und (27) entsprechen formal den Definitionen von Tangens und Cotangens, und
es gilt die Identität
|
cosh2x
−
sinh2x
= 1
für alle x ∈ R,
|
|
(28) |
die eine ganz ähnliche Struktur wie
sin2x
+ cos2x = 1 hat.
Tatsächlich widerspiegeln sie eine tiefe Verwandschaft der Exponentialfunktionen mit den
Winkelfunktionen, den wir in einem späteren Kapitel durch die Einbeziehung der
komplexen Zahlen aufdecken werden.
| | | |

komplexe Zahlen
| |
| | |
Die Funktion sinh besitzt bei x = 0 eine
Nullstelle, während cosh x
überall ≥ 1 ist. Der Graph von cosh heißt
Kettenlinie (sehen Sie ihn sich mit Hilfe des Funktions-Plotters an!),
da er die Form eines im Schwerefeld hängenden dünnen Seils hat.
Für große |x| nähern sich
sinh x und
cosh x asympotisch an
ex
an. tanh x und
coth x
streben im Unendlichen gegen 1. Bei x = 0
besitzt tanh eine Nullstelle und coth einen Pol erster Ordnung.
Die Inversen dieser Funktionen (die so genannten Areafunktionen: Arcus Sinus Hyperbolicus usw.)
lassen sich durch den natürlichen Logarithmen ausdrücken
(siehe nebenstehenden Button).
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Für gewisse Zwecke ist es notwendig, unstetige reelle Funktionen zu betrachten:
- Die (Heavisidesche) Theta-Funktion (oder kurz Sprungfunktion) ist definiert als
Sie wird in der Physik oft eingesetzt: Wird ein Signal zur Zeit
t = t0
abrupt eingeschaltet und hat danach den konstanten Wert 1, so wird sein zeitlicher Verlauf durch die Funktion
f (t)
=
θ (t
− t0)
beschrieben. Die genaue Definition der Theta-Funktion an der Stelle 0 ist dabei nicht
so wichtig (und in der Literatur manchmal auch anders gewählt).
Es gilt übrigens
θ (x)
+ θ (−x)
= 1 für alle x ∈ R.
(Versuchen Sie, das zu beweisen!)
- Die Signumfunktion (Vorzeichenfunktion) ist definiert als
Sie kann auch als sgn x =
θ (x)
− θ (−x)
definiert werden. (Versuchen Sie, das zu beweisen!)
Die Definition an der Stelle 0 wurde so gewählt, um sgn zu einer antisymmetrischen Funktion (s.o.)
zu machen.
| | | |
| |
| | |
- Charakteristische Funktionen: Ist M
eine Teilmenge von R, so wird definiert
- Treppenfunktionen weisen Sprungstellen auf, zwischen denen sie konstant sind.
Beispiele stellen die verschiedenen Rundungsverfahren dar:
- round − kaufmännisch runden: round x
ist diejenige ganze Zahl, die x am
nächsten liegt, wobei halbzahlige Werte zwischen zwei ganzen Zahlen aufgerundet werden.
- floor − immer abrunden: floor x
ist die "größte ganze Zahl, die kleiner-gleich x"
ist (oder einfach der "ganzzahlige Anteil" von x).
- ceil − immer aufrunden: ceil x
ist die "kleinste ganze Zahl, die größer-gleich x"
ist.
Zwischen den ersten beiden besteht die Beziehung
round x
= floor(x + 1/2).
Die Funktionsbezeichnungen sind gleichzeitig jene Namen
round, floor und
ceil (von engl. ceiling = die Zimmerdecke), die Sie im
Funktions-Plotter (um die Graphen anzuschauen)
und in unserem Taschenrechner JavaCalc
(zur Berechnung der numerischen Werte dieser Funktionen) benutzen können.
Allgemeinere Treppenfunktionen werden dazu benutzt, um den Begriff des Integrals genau zu definieren.
Weitere nützliche unstetige Funktionen werden uns im Zusammenhang mit Fourierreihen
begegnen.
|
| | |

Integral

Fourierreihen
| |
| | |
| Funktionen auf anderen Mengen |
| | | |
Zum Seitenanfang | |
| | |
Funktionen in mehreren Variablen
Funktionen können mehrere unabhängige Variable besitzen. Sie werden dann auch
als mehrstellig bezeichnet.
Sind beispielsweise x
und y zwei reelle Zahlen, so
ist ihr Abstand auf der Zahlengeraden durch die Formel
f (x, y) =
| x − y x − y |
gegeben. Formal handelt es sich dabei um eine Zuordnung
f : R |
gegeben. Formal handelt es sich dabei um eine Zuordnung
f : R 2 → R.
Sehen wir uns an, wie es dazu kommt: R 2 → R.
Sehen wir uns an, wie es dazu kommt: R 2 ist die Menge aller
reellen Zahlenpaare (x, y),
eine Menge, die wir auch als Zeichenebene kennen. Die Funktion f ordnet
jedem solchen Paar den Abstand der beiden Zahlen zu, aus denen es besteht: 2 ist die Menge aller
reellen Zahlenpaare (x, y),
eine Menge, die wir auch als Zeichenebene kennen. Die Funktion f ordnet
jedem solchen Paar den Abstand der beiden Zahlen zu, aus denen es besteht:
| | | |

R 2 2
| |
| | |
f :
(x,
y)
→
| x − y x − y | . | .
|
|
(32) |
Ein anderes Beispiel: Das Volumen eines Zylinders mit Radius
r und Höhe h ist durch die Formel
V(r, h) =
πr2h
gegeben. In diesem Fall ist der Definitionsbereich der Funktion V eine Teilmenge des R 2,
wenn wir uns auf positive r und h
beschränken wollen. Der Graph einer Funktion in zwei Variablen kann als Fläche
im dreidimensionalen Raum dargestellt werden: Jedem Punkt der Ebene, der durch ein Zahlenpaar
(x, y) oder
(r, h) festgelegt ist,
wird der Funktionswert
f 2,
wenn wir uns auf positive r und h
beschränken wollen. Der Graph einer Funktion in zwei Variablen kann als Fläche
im dreidimensionalen Raum dargestellt werden: Jedem Punkt der Ebene, der durch ein Zahlenpaar
(x, y) oder
(r, h) festgelegt ist,
wird der Funktionswert
f (x, y) oder
V(r, h)
als z-Koordinate in die dritte Richtung
("Höhe") zugeordnet. (x, y) oder
V(r, h)
als z-Koordinate in die dritte Richtung
("Höhe") zugeordnet.
Ein Beispiel für eine Funktion in drei Variablen ist die Masse eines solchen Zylinders in Abhängigkeit von seinen Abmessungen und seiner Dichte ρ:
M(r, h,
ρ) =
πr2h ρ.
Ganz allgemein stellt eine Funktion in n Variablen eine Zuordnung
f : A → B
dar, wobei A entweder
R n
(die Menge aller reellen "n-Tupel")
oder eine Teilmenge des R n
(die Menge aller reellen "n-Tupel")
oder eine Teilmenge des R n und B eine beliebige Menge ist. n und B eine beliebige Menge ist.
Wir erwähnen, dass die Werte einer Funktion beliebige mathematische Objekte sein können und nicht unbedingt Zahlen sein müssen.
Beispielsweise können Funktionen definiert werden, die jedem Element des R 3
ein anderes Element des R 3
ein anderes Element des R 3 zuordnen, also vom Typ
v :
R 3 zuordnen, also vom Typ
v :
R 3 → R 3 → R 3
sind. Eine solche Funktion wird manchmal als vektorwertig bezeichnet, da ihre Werte
Vektoren sind. 3
sind. Eine solche Funktion wird manchmal als vektorwertig bezeichnet, da ihre Werte
Vektoren sind.
| | | |

R n n

Vektoren
| |
| | |
Funktionen auf diskreten Mengen
Für viele Zwecke werden Funktionen benötigt, die auf einer diskreten Menge definiert sind,
d.h. auf einer endlichen Menge oder der Menge N der natürlichen Zahlen.
Wir besprechen drei Beispiele:
| | | |

N
| |
| | |
- Permutationen: Wenn n Personen auf n
Sesseln sitzen, dann alle aufstehen und sich (möglicherweise anders auf die Sesseln verteilt) wieder hinsetzen, handelt es sich
mathematisch gesprochen um eine Permutation. Formal ist eine Permutation (genauer: eine "Permutation von
n Elementen") eine bijektive Funktion
σ : M → M,
wobei M die Menge
{1, 2, ... n} ist. Beispielsweise
ist durch
|
σ(1) = 2,
σ(2) = 1,
σ(3) = 3
|
|
(33) |
eine Permutation von 3 Elementen definiert. (Ihr Wirkung besteht einfach darin, die ersten
beiden Elemente zu vertauschen).
- Folgen: Die "Aufzählung" der Elemente einer unendlichen Abfolge reeller Zahlen, wie
zum Beispiel (1, 1/4, 1/9, 1/16, 1/64, ...), können wir als
Funktion
a : N → R
auffassen. Der Funktionswert der natürlichen Zahl n wird
als die n-te Zahl der Liste definiert. So kann etwa das obige Beispiel
in der knappen Form
a(n) = 1/n2
beschrieben werden. Üblicherweise wird an
an Stelle von a(n) geschrieben.
Diese Art von Funktionen ist wichtig, wenn wir Begriffe wie das asymptotische Verhalten (s.o.) oder
ganz allgemein das "Unendliche" in der Mathematik genauer in den Griff bekommen möchten.
Ihnen ist ein eigenes Kapitel gewidmet.
| | | |

Folgen
| |
| | |
- Diskrete dynamische Modelle: Manchmal ist es sinnvoll, den zeitlichen Verlauf einer Größe
nicht mit Hilfe einer reellen (kontinuierlichen) Zeitvariable zu beschreiben, sondern in (diskreten) Schritten zu betrachten.
Ein Beispiel stellt eine Tierpopulation auf einer Insel dar:
Jedes Jahr im Frühling, nachdem die Jungen zur Welt gekommen sind, wird die Größe der Population ermittelt.
Im ersten Jahr beträgt ihre Anzahl x1,
im nächsten Jahr x2, usw.
Auch diese Abfolge können wir als Funktion auffassen.
x : A → R
auffassen, deren Definitionsbereich A entweder N oder eine
endliche Menge {1, 2, ... m} ist
(wenn die Polulation m Jahre lang beobachtet wird).
Sie ordnet jedem n ∈ A
den Wert
xn
zu.
| | | |

diskrete Modelle
(in Vorbereitung)
| |
| | |
Funktionen auf Mengen von Funktionen
Es sind aber auch Funktionen auf viel größeren Mengen als R
möglich. Ein einfaches Beispiel: Sei c eine festgehaltene reelle Zahl.
Ist eine Funktion
f : R → R
gegeben, so kann daraus eine andere Funktion
fc : R → R
konstruiert werden, und zwar durch die Definition
Der Graph von fc geht
aus jenem von f
durch eine Verschiebung um c in
x-Richtung hervor (s.o.).
Nun kann die Zuordnung
Tc : f → fc
selbst als Funktion aufgefasst werden! Sie operiert auf der Menge aller Funktionen vom Typ
f : R → R
und heißt Verschiebungsoperator.
(Funktionen werden in manchen Teilgebieten der Mathematik als "Operatoren" bezeichnet).
|
| | |

Operatoren
| |





































