| | |
| | | |
| |
| | |
| | | |
| |
| | |
Die naheliegendsten Anwendungen der Differentialrechnung bestehen darin,
Eigenschaften einer gegebenen reellen Funktion herauszufinden, die mit ihrer Ableitung, d.h. ihrer
Änderungsrate zu tun haben: In welchen Intervallen steigt oder fällt sie? Besitzt sie lokale Extrema
oder Sattelstellen und wenn ja, wo? Besitzt sie Wendestellen und wenn ja, wo?
Da Eigenschaften reeller Funktionen oft durch Eigenschaften ihrer Graphen ausgedrückt werden,
hat sich für diese Art von Funktionsuntersuchungen auch der Name Kurvendiskussionen eingebürgert.
Zu ihnen gehört auch das Auffinden anderer markanter Eigenschaften,
wie beispielsweise die Existenz und Lage von Nullstellen.
| | | |
| |
| | |
Wir werden in diesem ersten Abschnitt die wichtigsten Methoden zusammenstellen, dabei an früher Besprochenes erinnern
und auf Neues ausführlicher eingehen. Dazu
stellen wir uns vor, eine Funktion f
sei durch einen Term (Funktionsausdruck) gegeben.
Zur Bezeichnungsweise: Dabei wollen wir, wie üblich, die unabhängige Variable
x nennen und die beiden
Achsen der Zeichenebene als x- und y-Achse bezeichnen.
Wenn wir sagen, dass eine Stelle x1 "links"
(oder "rechts") von einer anderen Stelle x2 liegt, so meinen wir, dass
x1 < x2
(bzw. x1 > x2)
ist und beziehen uns damit auf die anschauliche Vorstellung der
x-Achse als Zahlengerade.
Ein wichtiger Tipp vorab: Wenn Sie die Eigenschaften einer Funktion
diskutieren sollen, legen Sie eine Zeichnung an und halten Sie alle Erkenntnisse,
die Sie im Zuge Ihrer Berechnungen gewinnen, in ihr fest!
Die nun folgende Liste von Themen steckt einen sinnvollen Rahmen für eine systematische Untersuchung ab.
Typ der Funktion
Handelt es sich um einen Ihnen bekannten Funktionstyp?
| | | |

Termdarstellung
| |
| | |
Eine große Klasse von Funktionen, die oft für Übungsaufgaben herangezogen werden, sind die rationalen Funktionen,
d.h. Quotienten von Polynomen (zu denen auch die Polynome als Spezialfälle gehören).
Falls es sich um eine solche handelt, können Sie die
Methoden, die wir bereits in einem frühreren Kapitel besprochen und in Form einer
Checkliste zusammengestellt haben, anwenden, um ihre Definitionslücken,
Nullstellen, Pole und Asymptoten aufzufinden.
Nullstellen
Die Nullstellen einer Funktion f sind
ganz allgemein durch die Lösungen der Gleichung
| | | |

Checkliste für
rationale Funktionen
| |
| | |
gegeben. Sie entsprechen jenen Punkten, an denen der Graph die x-Achse schneidet.
Falls Sie sich nicht mehr gut an dieses Thema erinnern, wiederholen Sie den Abschnitt
"Zusammenhang zwischen Funktionen und Gleichungen" aus dem ersten Funktionenkapitel.
Das Auffinden von Nullstellen hat zunächst nichts mit der Differentialrechnung zu tun.
Manche Gleichungen sind allerdings recht schwierig zu lösen,
und wir werden weiter unten sehen, dass die Differentialrechnung
für manche dieser Fälle eine effiziente Näherungsmethode bereitstellt.
| | | |

Funktionen und Gleichungen
| |
| | |
Sind die Nullstellen einer Funktion gefunden und ist die Funktion stetig, d.h.
ist ihr Graph eine zusammenhängende Linie, so sind damit auch die Bereiche,
in denen die Werte der Funktion positiv bzw. negativ sind, leicht zu ermitteln.
Dazu reicht es aus, das Vorzeichen an irgendwelchen Stellen zwischen den Nullstellen
zu berechnen. Besitzt die Funktion Singularitäten (Unendlichkeitsstellen), so
ist zu beachten, dass das Vorzeichen einer solchen Funktion auf beiden Seiten einer
Unendlichkeitsstelle gleich oder verschieden sein kann.
(Beispiele: Die durch
f(x) = 1/x
definierte Funktion besitzt keine Nullstelle, aber an der Stelle 0 eine Singularität und
kann beiderlei Vorzeichen annehmen. Die Funktion
f(x) = 1/x2
hat ebenfalls keine Nullstelle und an der Stelle 0 eine Singularität,
ist in ihrem Definitionsbereich aber überall positiv).
Lokale Extrema und Sattelstellen
| | | |

Singularitäten
und Pole
| |
| | |
Wir kommen nun zu einem Thema, in dem das Differenzieren eine wichtige Rolle spielt.
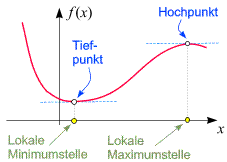 Gibt es eine Stelle, an der die Funktionswerte größer-gleich (kleiner-gleich)
als überall sonst sind? Wir nennen eine solche Stelle globale Maximumstelle (Minimumstelle).
Betrachten wir eine Funktion innerhalb eines Intervalls, so kann das globale Maximum
(Minimum) am Rand angenommen werden (für Beispiele siehe den Button rechts) . Darüberhinaus gibt es
noch die Möglichkeit, dass der Funktionswert an einer Stelle im Inneren
oder am Rand des Definitionsbereichs
größer-gleich (kleiner-gleich) als überall sonst in einer nahen Nachbarschaft dieser Stelle ist. Wir sprechen dann von einer
lokalen Maximumstelle (Minimumstelle). Die gemeinsame Bezeichnung ist lokale Extremstelle.
Vereinfachend kann man die Bezeichnung "stelle" weglassen und von einem
lokalen Maximum, Minimum oder Extremum sprechen.
Gibt es eine Stelle, an der die Funktionswerte größer-gleich (kleiner-gleich)
als überall sonst sind? Wir nennen eine solche Stelle globale Maximumstelle (Minimumstelle).
Betrachten wir eine Funktion innerhalb eines Intervalls, so kann das globale Maximum
(Minimum) am Rand angenommen werden (für Beispiele siehe den Button rechts) . Darüberhinaus gibt es
noch die Möglichkeit, dass der Funktionswert an einer Stelle im Inneren
oder am Rand des Definitionsbereichs
größer-gleich (kleiner-gleich) als überall sonst in einer nahen Nachbarschaft dieser Stelle ist. Wir sprechen dann von einer
lokalen Maximumstelle (Minimumstelle). Die gemeinsame Bezeichnung ist lokale Extremstelle.
Vereinfachend kann man die Bezeichnung "stelle" weglassen und von einem
lokalen Maximum, Minimum oder Extremum sprechen.
Ist f differenzierbar,
so ist an all diesen Stellen (sofern sie nicht am Rand des Definitionsbereichs liegen) die Tangente an den Graphen
parallel zur x-Achse, d.h.
hat den Anstieg 0.
Der Graph hat dort einen ''Gipfel'' (einen ''Talpunkt'').
Da die Ableitung den Anstieg der Tangente an den Graphen ausdrückt, sind die
Kandidaten für lokale Extrema die Lösungen der Gleichung
| | | |

differenzierbar

lokale Extrema
| |
| | |
Um also die lokalen Extrema der Funktion (die nicht am Rand des Definitionsbereich liegen) zu bestimmen, muss diese Gleichung zuerst gelöst werden.
Wir setzen nun voraus, dass jede Lösung isoliert ist, d.h. dass es für jede Lösung
ein Intervall (x − a, x + a) gibt
(eine so genannte Umgebung von x),
in dem die Ableitung nur an der Stelle x
verschwindet, ansonsten überall ≠ 0 ist.
Von jeder Lösung ist dann eigens zu überprüfen, ob es sich um ein lokales Maximum,
 ein lokales Minimum oder um keins von beiden handelt.
Dafür gibt es mehrere Methoden:
ein lokales Minimum oder um keins von beiden handelt.
Dafür gibt es mehrere Methoden:
- Im ersten Kapitel über das Differenzieren haben wir bereits ein Kriterium formuliert:
- Ist x eine Lösung der Gleichung
(2), und ist die Ableitung (innerhalb einer Umgebung von x)
links von x positiv und
rechts von x negativ,
so ist x eine lokale Maximumstelle.
Der entsprechenden Punkt am Graphen heißt Hochpunkt.
- Ist hingegen die Ableitung (innerhalb einer Umgebung von x)
links von x negativ und
rechts von x positiv,
so ist x eine lokale Minimumstelle.
Der entsprechenden Punkt am Graphen heißt Tiefpunkt.
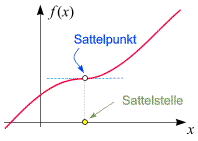
- Ist die Ableitung (innerhalb einer Umgebung von x)
links und rechts von x
ungleich 0 und hat in beiden Bereichen dasselbe Vorzeichen,
so ist x eine Sattelstelle.
Der entsprechenden Punkt am Graphen heißt Sattelpunkt.
| | | |

Charakterisierung von
Maximum-, Minimum-
und Sattelstellen
| |
| | |
Versuchen Sie bitte, die Begründung für dieses Verhalten zu verstehen!
Für den ersten Fall lautet sie so: Ist die Ableitung (innerhalb einer Umgebung von x)
links von x positiv und
rechts von x negativ,
so steigt die Funktion links von x
streng monoton an und fällt rechts von x
streng monoton ab. Zwischen diesen Bereichen (d.h. an der Stelle x)
ist die Ableitung 0
− der Graph hat also dort einen ''Gipfel'', d.h.
x ist eine lokale Maximumstelle.
Ganz analog funktioniert die Argumentation für den zweiten Fall.
Im dritten Fall wird angenommen, dass die Ableitung links und rechts von x
ungleich 0 ist und in beiden Bereichen dasselbe Vorzeichen
hat. Die Funktion ist also in einer Umgebung von x
monoton (wachsend oder fallend, je nach dem Vorzeichen der Ableitung) − der
Graph hat dort weder einen ''Gipfel'' noch einen ''Talpunkt''. Eine solche Stelle wird
Sattelpunkt genannt. Mit dem nebenstehenden Button können Sie zwei Beispiele aufrufen.
| | | |
| |
| | |
- Das in der Praxis einfachste Verfahren besteht darin, einige Funktionswerte konkret auszurechnen
und miteinander zu vergleichen. In den meisten Fällen ergibt sich daraus ganz eindeutig,
welche Kandidaten lokale Maximumstellen, welche lokale Minimumstellen und welche Sattelstellen sind.
Mit dem nebenstehenden Button können Sie vier Beispiele aufrufen.
| | | |
| |
| | |
- Ein drittes Verfahren benutzt die zweite Ableitung, d.h. die Ableitung der
Ableitung von f, die mit f ''
bezeichnet wird (und von der wir nun annehmen, dass sie existiert): Sei x eine
Lösung der Gleichung (2). Ist
so ist x eine lokale Maximumstelle.
Ist
so ist x eine lokale Minimumstelle.
Ist f ''(x) = 0,
so lässt sich daraus keine Aussage machen, ob es sich um ein lokales Maximum, ein lokales Minimum
oder um eine Sattelstelle handelt.
Um diese Methode anzuwenden, muss also zuvor f
zweimal differenziert und dann der Wert der zweiten Ableitung an der Kandidatenstelle x
berechnet werden. Das ist oft aufwendiger als die vorige Methode, wird aber leider manchmal
als einzige gelehrt.
| | | |
| |
| | |
Sind alle lokalen Maximum- und Minimumstellen, die der Gleichung (2) genügen,
gefunden (und werden − falls die Funktion nicht für alle reellen Zahlen definiert ist
− die Verhältnisse an den Randstellen des Definionsbereichs berücksichtigt), so läßt sich daraus
durch den Vergleich von Funktionswerten
leicht erschließen, ob die Funktion globale Maximumstellen (Minimumstellen) besitzt und wo sie liegen.
Tipp: Versuchen Sie, beim Auffinden von Extremstellen die jeweilige Situation, um die es sich handelt, zu verstehen,
um Ihre Vorgangsweise zu optimieren. Das erleichtert die Arbeit oft ganz erheblich!
Der nebenstehende Button ruft ein Beispiel auf, das auf zwei unterschiedliche Weisen
gelöst wird: Entscheiden Sie selbst, welche Ihnen sympathischer ist!
Anmerkung: Wichtig bei all diesen Methoden ist, dass
x eine isolierte Lösung der
Gleichung (2) ist. Wird diese Bedingung aufgegeben, so muss
x nicht unbedingt
Minimumstelle, Maximumstelle oder Sattelstelle sein, sondern es sind noch andere (kompliziertere) Fälle
möglich, wie das Beispiel
f(x) = x2sin(1/x)
für x ≠ 0
und f(0) = 0
für die Stelle x = 0
zeigt − sehen Sie sich
(z.B. mit dem Funktionsplotter)
ihren Graphen und den Graphen ihrer Ableitung an!
Monotoniebereiche
| | | |
spart Arbeit!
| |
| | |
Stellen Sie die bereits aufgefundenen lokalen Extremstellen (und gegebenenfalls Singularitäten)
in Rechnung, so ergeben sich die Bereiche, in denen die Ableitung positiv
(die Funktion daher streng monoton wachsend) bzw. negativ (die Funktion daher
streng monoton fallend) ist, praktisch von selbst.
Wendestellen
| | | |

Ableitung
und Monotonie
| |
| | |
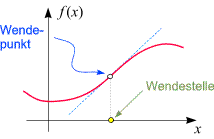
Wie bereits im ersten Kapitel über das Differenzieren bemerkt, kann sich die Tangente an den
Graphen an bestimmten Punkten von der einen Seite zur anderen ''wenden''. Die Punkte, an denen das
passiert, heißen Wendepunkte, die entsprechenden Stellen sind die Wendestellen.
Um sie uns zu veranschaulichen, können wir uns
einen Radfahrer vorstellen, der den Graphen entlang fährt. Dabei muss er manchmal nach links,
manchmal nach rechts lenken. Die Wendepunkte sind genau jene Punkte, an denen
er (momentan) geradeaus lenkt. An den entsprechenden Stellen besitzt die Ableitung
selbst ein lokales Extremum (d.h. die Tangente an den Graphen ist dort "am steilsten" bzw. "am wenigsten steil").
Kandidaten für die Wendestellen einer (zweimal differenzierbaren) Funktion
f sind die Lösungen der
Gleichung
| | | |

Wendestelle
| |
| | |
Wir setzen wieder voraus,
 dass jede Lösung isoliert ist, d.h. dass es für jede Lösung
ein Intervall (x − a, x + a) gibt
(eine Umgebung von x),
in dem die zweite Ableitung nur an der Stelle x
verschwindet, ansonsten überall ≠ 0 ist.
Von jeder Lösung ist dann eigens zu überprüfen, ob es sich tatsächlich um eine
Wendestelle handelt. Da eine Wendestelle von f ein
lokales Extremum von f '
ist, können wir eine der zuvor besprochenen Methoden auf
f ' (anstelle von
f ) anwenden:
dass jede Lösung isoliert ist, d.h. dass es für jede Lösung
ein Intervall (x − a, x + a) gibt
(eine Umgebung von x),
in dem die zweite Ableitung nur an der Stelle x
verschwindet, ansonsten überall ≠ 0 ist.
Von jeder Lösung ist dann eigens zu überprüfen, ob es sich tatsächlich um eine
Wendestelle handelt. Da eine Wendestelle von f ein
lokales Extremum von f '
ist, können wir eine der zuvor besprochenen Methoden auf
f ' (anstelle von
f ) anwenden:
- Das in der Praxis einfachste Verfahren besteht darin, einige Werte von
f ' konkret auszurechnen
und miteinander zu vergleichen, um festzustellen, ob die Stelle x
ein lokales Extremum von f '
ist.
- Ist x eine
Lösung der Gleichung (5) und
f '''(x) ≠ 0,
so ist x eine Wendestelle
von f. Ist
f '''(x) = 0, so
läßt sich daraus keine Aussage machen, ob es sich um eine Wendestelle
handelt.
In Übungsaufgaben wird meistens verlangt, zu jeder Wendestelle x
auch den Anstieg der Wendetangente, d.h. die Zahl
f '(x),
zu berechnen und anzugeben. Das ist beim Anlegen einer Zeichnung auch durchaus hilfreich.
Sattelpunkte sind Spezialfälle von Wendepunkten mit waagrechter Wendetangente:
Ist x eine Wendestelle und
f '(x) = 0,
so ist x eine Sattelstelle.
Krümmung und Konvexität
Fährt ein Radfahrer den Graphen einer differenzierbaren Funktion f entlang
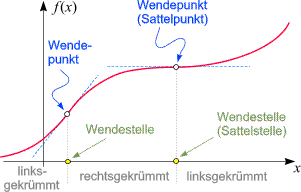 (in Richtung wachsender x-Werte), und
muss er innerhalb eines Bereiches immer nach links (rechts) lenken, so nennen wir
f in diesem Bereich
linksgekrümmt (rechtsgekrümmt). Formulieren wie diese Idee genauer: f
heißt in einem Intervall linksgekrümmt (rechtsgekrümmt), wenn die Ableitung
f ' in ihm streng monoton wachsend
(fallend) ist. Damit ergibt sich ein einfaches Kriterium zur praktischen Berechnung:
Ist für alle x in einem Intervall
f ''(x) > 0,
so ist f in diesem
Intervall linksgekrümmt. Ist für alle x in einem Intervall
f ''(x) < 0,
so ist f in diesem
Intervall rechtsgekrümmt.
Zeigt eine Funktion in zwei aneinander grenzenden Intervallen verschiedenes Krümmungsverhalten,
so liegt zwischen dieser Intervallen eine Wendestelle.
(in Richtung wachsender x-Werte), und
muss er innerhalb eines Bereiches immer nach links (rechts) lenken, so nennen wir
f in diesem Bereich
linksgekrümmt (rechtsgekrümmt). Formulieren wie diese Idee genauer: f
heißt in einem Intervall linksgekrümmt (rechtsgekrümmt), wenn die Ableitung
f ' in ihm streng monoton wachsend
(fallend) ist. Damit ergibt sich ein einfaches Kriterium zur praktischen Berechnung:
Ist für alle x in einem Intervall
f ''(x) > 0,
so ist f in diesem
Intervall linksgekrümmt. Ist für alle x in einem Intervall
f ''(x) < 0,
so ist f in diesem
Intervall rechtsgekrümmt.
Zeigt eine Funktion in zwei aneinander grenzenden Intervallen verschiedenes Krümmungsverhalten,
so liegt zwischen dieser Intervallen eine Wendestelle.
Hier besteht ein interessanter Zusammenhang zum Konvexitätsverhalten reeller Funktionen,
über das wir im zweiten Funktionenkapitel gesprochen haben. Wir nennen
f konvex (oder "nach oben offen"),
wenn jede Verbindungsstrecke zwischen zwei Punkten des Graphen von f an keiner Stelle
"unterhalb" dieses Graphen liegt und konkav ("nach unten offen"),
wenn jede Verbindungsstrecke zwischen zwei Punkten des Graphen von f an keiner Stelle
"oberhalb" dieses Graphen liegt.
Nun ist eine linksgekrümmte Funktion konvex (nach oben offen) und eine rechtsgekrümmte Funktion
konkav (nach unten offen). Das Konvexitätsverhalten einer differenzierbaren Funktion läßt sich daher über
eine Untersuchung des Vorzeichens ihrer zweiten Ableitung analysieren.
| | | |

konvex und konkav
| |
| | |
Allerdings gilt dieser Zusammenhang nicht in die umgekehrte Richtung: Eine konkave (konvexe) Funktion muss nicht
linksgekrümmt (rechtsgekrümmt) sein. Gegenbeispiele sind die konstanten Funktionen.
Sie sind gleichzeitig konkav und konvex, nicht aber gekrümmt.
Wir bezeichnen Funktionen nur dann als gekrümmt, wenn die Ableitung streng monoton
(wachsend oder fallend) ist.
Diese Konvention stimmt mit der anschaulichen Bedeutung des Begriffs "gekrümmt"
(als Gegensatz zu "gerade") überein.
In einem anderen Kapitel wird ein Maß für
die Krümmung einer Kurve besprochen. Hier können wir es bei der
intuitiven Formulierung belassen, dass die zweite Ableitung einer reellen Funktion ein quantitatives Maß
dafür darstellt, wie sehr sich ihr Graph von einer Geraden unterscheidet.
(Ist sie an allen Stellen eines Intervalls gleich 0,
so hat f dort eine
konstante Ableitung, und folglich ist der Graph von f
in diesem Intervall eine Gerade. Allerdings ist bei der intuitiven Formulierung
"zweite Ableitung = Maß für die Abweichung von der Geradenform" Vorsicht geboten, wenn
die Ableitung der Funktion sehr groß ist. Das läßt sich anhand der
Funktion f(x) = x2
erkennen: Ihre zweite Ableitung ist 2, also konstant, ihr
Graph wird aber für große x immer
"geradliniger").
|
| | |

Krümmung
einer Kurve
(in Vorbereitung)
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Eine der interessantesten Eigenschaften von Funktionen ist, wie im vorigen Abschnitt besprochen,
das Vorhandensein lokaler Extrema. In vielen praktischen Anwendungen der Mathematik
geht es darum, Gewinne zu maximieren und Kosten zu minimieren, aber auch aus
anderen Gründen möchte man gern wissen, wie eine Größe,
die von anderen Größen abhängt, maximal oder minimal gemacht werden kann.
Problemstellungen dieses Typs werden Extremwertaufgaben (oder auch
Optimierungsaufgaben) genannt.
| | | |
| |
| | |
Dabei
 hängt die Größe, die maximiert oder minimiert (kurz: optimiert) werden soll, die
Zielfunktion, in der Regel von mehreren Variablen ab, zwischen denen
Zusammenhänge (Nebenbedingungen) bestehen.
Die Aussage, dass die Zielfunktion maximal/minimal sein soll, wird manchmal auch als
Hauptbedingung bezeichnet.
Betrachten wir ein einfaches
− aber typisches − Beispiel:
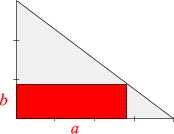
In ein rechtwinkeliges Dreieck (dessen Katheten die Längen 3 und 4 haben)
soll − wie in der nebenstehenden Graphik dargestellt −
ein Rechteck eingeschrieben werden. Wie ist es zu wählen, damit seine Fläche
(die Zielfunktion) maximal ist?
Im Folgenden führen wir einen Lösungsweg vor, der im Prinzip bei vielen derartigen
Aufgaben angewandt werden kann.
Die geometrische Bedeutung dessen, was wir nun berechnen werden, können Sie sich
im nebenstehenden Applet ansehen.
hängt die Größe, die maximiert oder minimiert (kurz: optimiert) werden soll, die
Zielfunktion, in der Regel von mehreren Variablen ab, zwischen denen
Zusammenhänge (Nebenbedingungen) bestehen.
Die Aussage, dass die Zielfunktion maximal/minimal sein soll, wird manchmal auch als
Hauptbedingung bezeichnet.
Betrachten wir ein einfaches
− aber typisches − Beispiel:
In ein rechtwinkeliges Dreieck (dessen Katheten die Längen 3 und 4 haben)
soll − wie in der nebenstehenden Graphik dargestellt −
ein Rechteck eingeschrieben werden. Wie ist es zu wählen, damit seine Fläche
(die Zielfunktion) maximal ist?
Im Folgenden führen wir einen Lösungsweg vor, der im Prinzip bei vielen derartigen
Aufgaben angewandt werden kann.
Die geometrische Bedeutung dessen, was wir nun berechnen werden, können Sie sich
im nebenstehenden Applet ansehen.
- Die Fläche f des Rechtecks, die Zielfunktion,
ist das Produkt aus den Seitenlängen.
Bezeichnen wir letztere wie in der Graphik mit a und b,
so wird
Das gilt für jedes in das Dreieck eingeschriebene Rechteck.
| | | |
Applet
Schema einer Extremwertaufgabe
| |
| | |
- Die Seiten a und b
des Rechtecks sind nicht voneinander unabhängig. Wird beispielsweise a
vorgegeben, so ist b damit bereits
festgelegt (und umgekehrt). Das führt zur Nebenbedingung, dem Zusammenhang zwischen den
Größen, von denen die Zielfunktion abhängt.
Sie muss beschreiben, welchen Wert a
hat, wenn b vorgegeben ist, bzw.
welchen Wert b
hat, wenn a vorgegeben ist.
In unserem Beispiel ergibt sie sich
aus den im gegebenen Dreieck auftretenden Ähnlichkeitsverhältnissen:
Wir entnehmen der folgenden Skizze
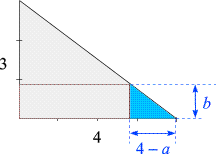 die Beziehung
die Beziehung
lösen sie nach b auf und erhalten
Diese Formel beschreibt, welchen Wert b
annimmt, wenn a vorgegeben wird.
| | | |

Ähnlichkeit
| |
| | |
- Damit ist das Problem auf eine einzige unabhängige Variable, nämlich a,
reduziert. Wir setzen b in den Term (6)
für die Zielfunktion ein. Diese vereinfacht sich damit zu einer Funktion in einer einzigen Variablen. Wir
bezeichnen sie ebenfalls mit dem Buchstaben f :
|
f(a) = (3/4) × a (4 − a). |
|
(9) |
| | | |
| |
| | |
- Das gestellte Problem nimmt nun die folgende formale Form an: An welcher Stelle besitzt die Funktion
f ein globales Maximum?
| | | |
| |
| | |
- Da f als Polynomfunktion differenzierbar
ist, erfolgt die Lösung dieses Problems so, wie wir es oben besprochen haben
(wobei die Variable nun nicht x, sondern
a heißt):
- f nach a differenzieren:
f '(a) = (3/4) × (4 − 2a).
- Die Gleichung f '(a) = 0
lösen: Als einzige Lösung ergibt sich a = 2.
- Sicherstellen, dass a = 2 das
gesuchte Maximum ist:
An den Rändern des Intervalls 0 ≤ a ≤ 4,
außerhalb dessen das Problem keinen Sinn macht, ergibt sich
f(0) = f(4) = 0.
An der Kandidatenstelle ist
f(2) = (3/4) × 2 (4 − 2) = 3,
was größer als
0 ist. Da es keinen anderen Kandidaten für ein lokales Extremum gibt,
muss a = 2 eine globale Maximumstelle sein
− an keiner anderen Stelle kann die Funktion f
größer oder gleich 3 sein.
- Die Werte der noch unbestimmten Variablen bestimmen: Aus (8) ergibt sich
b = (3/4) × (4 − 2) = 3/2.
- Die Lösung interpretieren, eine Zeichnung der Lösungsfigur anlegen
(das lassen wir Ihnen über) und − wenn möglich −
in Worte fassen: Das Rechteck mit der maximalen Fläche ergibt sich, wenn seine Seitenlängen
mit den halben Kathetenlängen übereinstimmen.
Zusätzlicher Check anhand der Zeichnung: Der maximale Wert der Fläche, 3, ist gleich
einem Viertel der Dreiecksfläche.
| | | |
| |
| | |
Der hier dargestellte Lösungsweg ist nicht der einzig mögliche. Beispielsweise hätten wir
aus (7)
a durch b
ausdrücken können (statt umgekehrt) und dann statt (9) eine von b
abhängige Funktion untersuchen müssen. Führen Sie diese Variante zur Übung selbst
durch!
Der schwierigste Punkt bei der Bewältigung von Extremwertaufgaben besteht meist darin, die
Nebenbedingung zu finden. Dabei ist es oft nötig, geometrische Beziehungen
aufzuspüren, Ähnlichkeitsverhältnisse anszunutzen (wie wir es im obigen Beispiel gemacht haben),
falls ein Kreis im Spiel ist: den Pythagoräischen Lehrsatz anzuwenden und dergleichen mehr.
Leider gibt es keine allgemeine Regel dafür. Manchmal hängt die Zielfunktion
zu Beginn von mehr als zwei Variablen ab, so dass mehr als eine Nebenbedingung gefunden werden muss,
um die Zielfunktion durch eine einzige Variable auszudrücken.
Der nebenstehende Button ruft ein weiteres, etwas komplizierteres Beispiel auf.
In einem späteren Kapitel werden wir mit Hilfe des Konzepts der "partiellen Ableitung"
eine andere (sehr elegante) Methode zur Lösung von Extremwertaufgaben (die so genannte
"Methode der Lagrangeschen Multiplikatoren") vorstellen. Dort werden wir allgemeinere
Optimierungsaufgaben, deren Zielfunktion auch nach der Auswertung aller
Nebenbedingungen von mehreren Variablen abhängt, lösen.
(Beispiel: Die Form eines Berges wird als Graph der Funktion
f(x, y) = 1 − x2 − x + x y − y2 ,
d.h. als Fläche im R3 beschrieben, wobei
x und y
die Koordinaten auf der Landkarte sind. Wo befindet sich der
Gipfel des Berges? Hier gibt es überhaupt keine Nebenbedingung).
|
| | |

partielle Ableitung
(in Vorbereitung)
| |
| | |
| Grenzwerte unbestimmter Formen |
| | | |
Zum Seitenanfang | |
| | |
Die Differentialrechnung wird für zahlreiche Zwecke innerhalb der Mathematik eingesetzt.
Als Beispiel für eine solche werden wir nun eine erstaunliche Formel besprechen.
Betrachten wir zwei reelle Funktionen
f und
g, die beide in einer Umgebung der
Stelle x0, d.h. in einem Intervall
(x0 − a, x0 + a),
stetig differenzierbar sind und beide
an der Stelle x0
verschwinden, d.h.
f(x0) = g(x0) = 0
erfüllen. Dann betrachten wir den Quotienten
f(x)/g(x).
Er ist an der Stelle x0 nicht
wohldefiniert. Wird versucht, für x den Wert
x0 einzusetzen,
so entsteht die "unbestimmte Form 0/0", also ein
sinnloser Ausdruck.
| | | |

stetig differenzierbar
| |
| | |
Es ist aber durchaus möglich, dass der Grenzwert dieses Quotienten für
x → x0
existiert, d.h. dass sich f(x)/g(x)
einer wohldefinierten Zahl annähert, wenn x gegen
x0 strebt.
Das ist beispielsweise für die Funktionen
f(x) = x + x2,
g(x) = x
an der Stelle x0 = 0
der Fall: Für x ≠ 0
ist f(x)/g(x) = 1 + x,
was im Limes x → 0
gegen 1 strebt. Es handelt sich hier um eine
Definitionslücke, die "stetig geschlossen" werden kann.
Für solche Situationen maßgeschneidert ist die Formel
| | | |

Grenzwerte reeller Funktionen

Definitionslücke
| |
| | |
| |
|
f(x)
g(x) |
= |
|
|
f '(x)
g'(x) |
, |
| lim |
lim |
| x → x0 |
x → x0 |
|
(10) |
wobei lediglich vorausgesetzt ist, dass der Grenzwert auf der rechten Seite existiert.
Sie heißt Regel von de l'Hospital (ausgesprochen [dö lopital]).
Um sie anzuwenden, müssen Zähler und Nenner durch ihre Ableitungen ersetzt
und danach der Grenzwert ausgeführt werden. Dieser ist aber oft leichter
zu berechnen als der ursprüngliche. Insbesondere kann es geschehen, dass
g'(x0) ≠ 0 ist.
Dann ist die rechte Seite von (10) einfach
f '(x0)/g'(x0).
Ist der Quotient f '(x)/g'(x)
selbst wieder eine unbestimmte Form, so kann die Formel auch auf ihn angewandt werden,
wobei ein weiteres Mal Zähler und Nenner durch ihre Ableitungen zu ersetzen sind.
Mit dieser Methode können Grenzwerte berechnet werden, die ansonsten schwierig zu behandeln
wären.
Beispiel 1 :
| |
|
sin x
x |
= |
|
|
cos x
1 |
= |
cos 0
1 |
= 1 |
. |
| lim |
lim |
| x → 0 |
x → 0 |
|
(11) |
| | | |
| |
| | |
Dabei haben wir verwendet, dass
sin'(x) = cos x
ist. Der zweite Grenzwert kann direkt ausgeführt werden, indem Zähler und Nenner an der Stelle
x = 0 ausgewertet werden.
Dasselbe Resultat (mit dem einzigen Unterschied, dass die Variable als
ε bezeichnet war) haben wir im ersten Kapitel über das Differenzieren
mit anderen Mitteln erzielt. (Es war notwendig, um die Ableitung der Sinusfunktion zu berechnen).
Beispiel 2 :
| |
|
cos x − 1
x2 |
= |
|
|
− sin x
2x |
= |
| lim |
lim |
| x → 0 |
x → 0 |
|
|
| |
|
| = |
|
|
− cos x
2 |
= |
− cos 0
2 |
= − |
1
2 |
. |
| lim |
| x → 0 |
|
|
(12) |
Hier führt auch der zweite Ausdruck auf eine unbestimmte Form, und erst nach einer weiteren Anwendung des Satzes
(10), d.h. einer weiteren Differentiation,
ergibt sich der Grenzwert durch simples Einsetzen von x = 0.
Aus diesem Resultat folgt übrigens, dass für kleine
x
| | | |

Ableitung der Sinusfunktion
| |
| | |
ist. Vergleichen Sie die Graphen der Funktionen
cos x
und 1 − x2/2
(z.B. mit dem Funktionsplotter) !
Überlegungen dieser Art sind auch in einem anderen Kapitel, das den so genannten Potenzreihen gewidmet ist,
wichtig.
| | | |

Potenzreihen
| |
| | |
Nachbemerkungen: Regel (10) gilt auch dann, wenn die Bedingungen
f(x0) = g(x0) = 0
durch
limx → x0 | f(x)|
=
limx → x0 |g(x)|
= ∞
ersetzt werden. Damit können Grenzwerte "unbestimmter Formen ∞/∞"
berechnet werden. Weiters darf
x0 durch
∞ oder −∞
ersetzt werden.
Einige Beispiele, unter denen auch
"unbestimmte Formen 0 × ∞"
vorkommen, und die
der Aufstellung weiterer Näherungsformeln und dem Wachstumsvergleich von
Funktionen dienen,
können Sie mit dem nebenstehenden Button aufrufen.
Online-Werkzeug: Im Rahmen des an der Vanderbilt University zur Verfügung gestellten
MathServ Project
finden Sie das auf Mathematica beruhende
Programm Computing a Limit,
mit dessen Hilfe Sie Grenzwerte unbestimmter Formen berechnen können.
|
| | |
| |
| | |
| Newton-Verfahrung zur Lösung von Gleichungen |
| | | |
Zum Seitenanfang | |
| | |
Für viele inner- und außermathematische Zwecke müssen wir Gleichungen lösen.
Eine Gleichung in einer reellen Unbekannten zu lösen, ist äquivalent zum Problem, die Nullstellen
einer reellen Funktion zu finden. Eine solche Gleichung kann daher immer in der Form
| | | |

Gleichungen und
Nullstellen
| |
| | |
geschrieben werden. Wie in einem früheren Kapitel besprochen, können manche
Gleichungstypen (z.B. lineare und quadratische) systematisch behandelt und exakt gelöst werden.
Leider ist das nicht für jede Gleichung der Fall. Oft ist man auf
Näherungsverfahren angewiesen.
Wir haben früher bereits die graphische Methode erwähnt (die allerdings
in der Genauigkeit beschränkt ist und schlecht automatisiert werden kann).
Die Bisektionsmethode funktioniert für stetige Funktionen immer,
ist aber nicht besonders schnell. Für den Fall, dass f
differenzierbar ist, steuert die Differentialrechnung eine weitere Methode,
das so genannte Newtonsche (Näherungs-)Verfahren, bei.
In vielen Fällen gestattet es, die Nullstellen einer Funktion sehr rasch mit
hoher Genauigkeit zu ermitteln.
| | | |

graphisches Lösen
von Gleichungen
| |
| | |
Wir erläutern
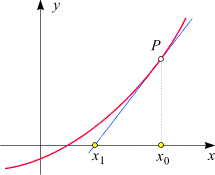 es anhand des nebenstehenden Diagramms. Zunächst brauchen wir einen
Startwert − in der Regel wählt man eine Schätzung für die gesuchte Nullstelle.
Wir bezeichnen ihn mit x0.
Nun denken wir uns durch den Punkt
(x0, f(x0)),
im Diagramm mit P bezeichnet,
die Tangente an den Graphen von f gelegt.
Ihr Schnittpunkt mit der x-Achse ergibt
eine Stelle x1,
die − wie in unserem Diagramm und auch in vielen praktischen Fällen −
näher an der gesuchten Nullstelle liegt als x0.
Sehen wir uns an, wie x1 aus x0
berechnet wird: Die Gleichung der
Tangente durch den Punkt (x0, f(x0))
ist y − f(x0)
= f '(x0) (x − x0).
(Um das zu überprüfen, setzen Sie
x = x0 und
y = f(x0) in sie ein!)
Diese Gerade schneidet die x-Achse
im Punkt (x1, 0).
Um x1 zu erhalten, setzen wir
y = 0 und lösen nach
x auf: Wir erhalten
x1 = x0
− f(x0)/f '(x0).
Um eine bessere Näherung x2 zu erhalten, können wir
dasselbe Verfahren auf x1 anwenden, was auf
x2 = x1
− f(x1)/f '(x1)
führt. Klicken Sie hier, um die Anzeige
dieses besseren Näherungswerts in der obigen Skizze an- und abzuschalten.
es anhand des nebenstehenden Diagramms. Zunächst brauchen wir einen
Startwert − in der Regel wählt man eine Schätzung für die gesuchte Nullstelle.
Wir bezeichnen ihn mit x0.
Nun denken wir uns durch den Punkt
(x0, f(x0)),
im Diagramm mit P bezeichnet,
die Tangente an den Graphen von f gelegt.
Ihr Schnittpunkt mit der x-Achse ergibt
eine Stelle x1,
die − wie in unserem Diagramm und auch in vielen praktischen Fällen −
näher an der gesuchten Nullstelle liegt als x0.
Sehen wir uns an, wie x1 aus x0
berechnet wird: Die Gleichung der
Tangente durch den Punkt (x0, f(x0))
ist y − f(x0)
= f '(x0) (x − x0).
(Um das zu überprüfen, setzen Sie
x = x0 und
y = f(x0) in sie ein!)
Diese Gerade schneidet die x-Achse
im Punkt (x1, 0).
Um x1 zu erhalten, setzen wir
y = 0 und lösen nach
x auf: Wir erhalten
x1 = x0
− f(x0)/f '(x0).
Um eine bessere Näherung x2 zu erhalten, können wir
dasselbe Verfahren auf x1 anwenden, was auf
x2 = x1
− f(x1)/f '(x1)
führt. Klicken Sie hier, um die Anzeige
dieses besseren Näherungswerts in der obigen Skizze an- und abzuschalten.
x2 dient als Ausgangpunkt für
einen noch besseren Näherungswert x3, usw.
Das Verfahren wird so lange fortgesetzt, bis die gewünschte Genauigkeit erreicht ist.
Insgesamt erhalten wir also folgende Rekursionsformel:
| | | |

Rekursion
| |
| | |
| |
xn + 1 = xn − |
f(xn)
f '(xn) |
. |
|
(15) |
Das Verfahren ist so einfach, dass es von Computern ausgeführt werden kann, und es führt oft nach
wenigen Schritten zu sehr genauen Näherungswerten.
Online-Werkzeuge:
- Um dem Algorithmus bei der Arbeit zuzusehen und es an
verschiedenen Funktionen auszuprobieren, benutzen Sie das
(von unseren Innsbrucker Projektpartnern gestaltete) Applet zum
Newtonverfahren.
(Anstelle eines Startwerts müssen Sie ein Intervall angeben, wie die vorbereiteten Beispiele
zeigen).
- Im Rahmen des an der Vanderbilt University zur Verfügung gestellten
MathServ Project
finden Sie das auf Mathematica beruhende
Online-Werkzeug Using Newton's Method.
Achtung:
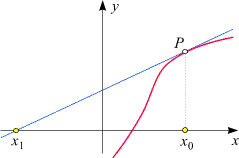 Die Methode funktioniert nicht immer! Wie das nebenstehende Diagramm illustriert,
kann x1 von
der gesuchten Nullstelle weiter entfernt liegen als x0.
In manchen Fällen muss lediglich der Startwert x0
genügend nahe an der gesuchten Nullstelle liegen, in anderen Fällen
führt die Methode für keinen Startwert zum Ziel.
Die Methode funktioniert nicht immer! Wie das nebenstehende Diagramm illustriert,
kann x1 von
der gesuchten Nullstelle weiter entfernt liegen als x0.
In manchen Fällen muss lediglich der Startwert x0
genügend nahe an der gesuchten Nullstelle liegen, in anderen Fällen
führt die Methode für keinen Startwert zum Ziel.
Übungsaufgabe: Geben Sie in das oben erwähnte Applet zum Newtonverfahren
als Funktionsausdruck abs(x)^(3/2)/x
ein, wählen Sie ein beliebiges Intervall der Form [-a,a],
klicken Sie auf "zeichnen", dann auf "Newton", und interpretieren Sie, was Sie sehen!
Es gibt verschiedene Kriterien, die die Konvergenz des Verfahrens garantieren.
Wir wollen hier nur eines erwähnen:
Ist die (differenzierbare) Funktion f innerhalb eines offenen Intervalls, in dem
genau eine Nullstelle x* liegt,
konvex (konkav), so konvergiert die Folge
(x0, x1, x2, ...)
der Näherungswerte gegen x*, wenn der Startwert
x0 innerhalb dieses
Intervalls so gewählt wird, dass
f(x0)
positiv (negativ) ist.
Berechnung der Quadratwurzel
Um das Verfahren in einem praktischen Zusammenhang zu illustrieren, zeigen wir, wie ein
Computer die Quadratwurzel einer gegebenen Zahl a > 0 im Bruchteil einer Sekunde auf zehn Stellen genau berechnet.
Dazu betrachten wir die Funktion
f(x) = x2 − a,
deren (einzige) positive Nullstelle √a
ist. Mit f '(x) = 2x
erhalten wir aus (15) nach einer kleinen Umformung die Rekursionsformel
| |
xn + 1 = |
1
2 |
( |
xn + |
a
xn |
) . |
|
(16) |
Als Startwert wählen wir x0 = 1.
Der Computer braucht nichts anderes zu machen, als die in (16) vorgeschriebenen
Rechenschritte, in denen nur die Grundrechnungsarten vorkommen, so lange auszuführen,
bis sich am Ergebnis zweier aufeinanderfolgender Schritte im Rahmen
der Rechnergenauigkeit nichts mehr ändert.
Dieser Algorithmus konvergiert sehr schnell.
Wählen wir als Beispiel a = 2, so finden
wir, dass bereits x3 nur um
0.0000021 von
√2 abweicht,
x4 nur mehr um
1.6 × 10−12.
Beachten Sie, dass uns die Differentialrechnung zu dieser Methode geführt hat,
der Computer bei der Ausführung aber natürlich nicht differenzieren muss.
Der nebenstehende Button ruft ein kleines JavaScript-Programm auf, das (16) ausführt, und
das Sie in unserem Rechner
JavaCalc laufen lassen können.
| | | |

Wurzelziehen mit Folgen
Programm
| |
| | |
Versuchen Sie als Übungsaufgabe, einen Näherungsalgorithmus
für die Berechnung der dritten Wurzel zu finden!
Weiteres über die numerische Berechnung von Nullstellen wird in einem anderen Kapitel
besprochen.
|
| | |

numerische Methoden
(in Vorbereitung)
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Die Differentialrechnung spielt in vielen Anwendungen der Mathematik eine entscheidende Rolle, und sie erlaubt es auch,
neue Begriffe zu prägen.
Bereits ihre Entwicklung durch Isaac Newton im Jahr 1666 war eng mit der Suche nach den
physikalischen Bewegungsgesetzen verbunden.
Sehen wir uns das genauer an: Bewegt sich ein Körper der Masse
m unter dem Einfluss einer Kraft
K(t) (die von
der Zeit abhängen darf) so, dass er zur Zeit t
am Ort s(t) ist,
so gilt
Das ist das berühmte "Zweite Newtonsche Gesetz" der Mechanik.
Dabei ist s'' die Beschleunigung des Körpers.
Die Kraft tritt hier als Ursache der Beschleunigung (und nicht als Ursache der Geschwindigkeit wie in der aristotelischen
und mittelalterlichen Physik) auf.
Um Gleichungen (genauer: Differentialgleichungen) dieser Art überhaupt anschreiben zu können,
entwickelte Newton die Idee der Ableitung. Den Namen "Differentialrechnung" erhielt die neue Theorie
erst später von Gottfried Wilhelm von Leibniz, der sie unabhängig von Newton
im Jahr 1675 entwickelte. Heute ist sie aus der Modellierung von Bewegungs- und Entwicklungsvorgängen
nicht mehr wegzudenken.
|
| | |

Differentialgleichungen
(in Vorbereitung)

dynamische Systeme
(in Vorbereitung)
| |