| | |
| | | |
| |
| | |
| Stammfunktion (unbestimmtes Integral) |
| | | |
| |
| | |
Wir formulieren zunächst die Idee, den Prozess des Differenzierens "umzukehren". Ist
f eine gegebene reelle Funktion, und ist
F eine Funktion, deren Ableitung
f ist, d.h.
für alle x im Definitionsbereich von f,
so nennen wir F eine Stammfunktion von f.
Beispiel:
F(x) = x3
ist eine Stammfunktion von
f(x) = 3x2, denn
(x3) ' = 3x2.
Beachten Sie: G(x) = x3 + 1
ist ebenfalls eine Stammfunktion von
f(x) = 3x2, denn
(x3 + 1) ' = 3x2.
Wie dieses Beispiel zeigt, ist die Stammfunktion nicht eindeutig - eine Funktion
kann mehrere Stammfunktionen haben. Tatsächlich folgt aus der Existenz einer Stammfunktion,
dass sie mehrere hat, und es gilt:
| | | |

differenzieren
| |
| | |
Ist F
eine Stammfunktion von f,
so ist jede Stammfunktion von f
von der Form
wobei c eine Konstante ist. |
Wir bezeichnen die Stammfunktion als unbestimmtes Integral und verwenden für sie die Schreibweise
(ausgesprochen: "Integral von f(x)"
oder "Integral f(x) dx"). dx").
Beispiel:
Der Zusatz " + c" soll anzeigen, dass
die Stammfunktion nur bis auf eine (beliebige) Konstante (die so genannte Integrationskonstante) eindeutig ist.
Er wird manchmal der Einfachheit halber weggelassen (sollte aber dann zumindest dazugedacht werden).
Der Vorgang, eine Stammfunktion zu einer gegebenen Funktion zu finden, heißt integrieren.
(Dieses Wort wird später noch eine zusätzliche Bedeutung erhalten).
Der Ausdruck zwischen dem Integralzeichen ò und dem Symbol dx
(zu deren Bedeutung wir weiter unten noch etwas sagen werden)
heißt Integrand ("zu integrierende Funktion").
Man kann auch sagen, eine Funktion wird nach x
integriert, um die Variable, um die es geht, zu benennen. Bisweilen wird auch die
(in mancher Hinsicht günstigere) Schreibweise
verwendet. Bei ihr kann die Kombination der Symbole ò dx
als Aufforderung verstanden werden, die darauf folgende Funktion
nach x zu integrieren. dx
als Aufforderung verstanden werden, die darauf folgende Funktion
nach x zu integrieren.
| | | |
| |
| | |
Wir werden einige Regeln für das Integrieren weiter unten kennen lernen,
schicken aber hier die wichtigste Methode voraus: Benutzen Sie alles, was Sie über
Ableitungsregeln und über die Ableitungen spezieller Funktionen wissen!
Stammfunktionen können oft erraten werden. Steht Ihnen eine Tabelle von
Ableitungen wie diese
zur Verfügung, so können Sie die einzelnen Zeilen "von rechts nach links" lesen:
Ist f die Ableitung von F,
so ist F eine Stammfunktion von
f.
Beispiel: Um eine Stammfunktion von x + 3 sin x
zu finden, suchen Sie in der Tabelle (oder in Ihrem Gedächtnis) Funktionen, deren Ableitungen mit den einzelnen Summanden
(möglicherweise bis auf Vielfache) übereinstimmen.
So erinnern Sie sich etwa, sin x
zu finden, suchen Sie in der Tabelle (oder in Ihrem Gedächtnis) Funktionen, deren Ableitungen mit den einzelnen Summanden
(möglicherweise bis auf Vielfache) übereinstimmen.
So erinnern Sie sich etwa,
- dass die Ableitung von
x2 gleich
2x ist, die Ableitung von
x2/2 daher gleich
x.
-
Weiters ist die Ableitung von cos x gleich
-sin x,
die Ableitung von
-3
 cos x
daher gleich
3 cos x
daher gleich
3 sin x. sin x.
- Setzen wir diese Erkenntnisse zusammen, so ergibt sich: Die Ableitung von
x2/2 - 3
 cos x
ist gleich
x + 3 cos x
ist gleich
x + 3 sin x, d.h.
gleich der gegebenen Funktion. sin x, d.h.
gleich der gegebenen Funktion.
Die Antwort lautet daher:
| ò |
(x +
3 sin x) dx
= x2/2 -
3 sin x) dx
= x2/2 -
3 cos x
+ c . cos x
+ c . |
|
(6) |
Wenn Sie das für ein paar Beispiele dieser Art durchgehen, werden sie selbst Regeln für das Integrieren
(und vielleicht auch einige Schwierigkeiten, die es vom Differenzieren unterscheiden) entdecken.
Stammfunktionen, die oft benötigt werden, sollten Sie sich auswendig merken, insbesondere:
- Potenzen: ò
 1 1 dx = x,
ò dx = x,
ò x x dx = x2/2 und
ò dx = x2/2 und
ò x2 x2 dx = x3/3. dx = x3/3.
- Winkelfunktionen: ò
 sin sin x x dx =
- dx =
- cos cos x
und
ò x
und
ò cos cos x x dx =
sin dx =
sin x. x.
Versuchen Sie als Übungsaufgabe, die allgemeine Potenzfunktion
f(x) = xn
zu integrieren!
|
| | |

Ableitung spezieller
Funktionen
| |
| | |
| Flächenberechnung (bestimmtes Integral) |
| | | |
Zum Seitenanfang | |
| | |
Betrachten wir nun
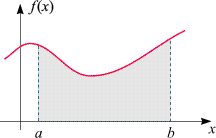 ein (auf den ersten Blick) ganz anderes, das so genannte Flächeninhaltsproblem: Gegeben sei eine reelle Funktion
f, und wir wollen den Inhalt der Fläche unter ihrem Graphen im Intervall
a £ x £ b
bestimmen, wie in der nebenstehenden Skizze dargestellt.
Wir werden weiter unten darüber sprechen, wie ein solcher Flächeninhalt
mathematisch präzise definiert werden kann
und merken lediglich an, dass dieser Idee für sehr viele Funktionen,
darunter für alle stetigen und stückweise stetigen, aber auch
für andere, ein präziser Sinn gegeben werden kann.
Im Fall von Funktionen, deren Graph einen (zumindest stückweise) glatten Verlauf hat,
gibt uns unsere geometrische Anschauung eine intuitive Vorstellung davon, was damit gemeint ist.
ein (auf den ersten Blick) ganz anderes, das so genannte Flächeninhaltsproblem: Gegeben sei eine reelle Funktion
f, und wir wollen den Inhalt der Fläche unter ihrem Graphen im Intervall
a £ x £ b
bestimmen, wie in der nebenstehenden Skizze dargestellt.
Wir werden weiter unten darüber sprechen, wie ein solcher Flächeninhalt
mathematisch präzise definiert werden kann
und merken lediglich an, dass dieser Idee für sehr viele Funktionen,
darunter für alle stetigen und stückweise stetigen, aber auch
für andere, ein präziser Sinn gegeben werden kann.
Im Fall von Funktionen, deren Graph einen (zumindest stückweise) glatten Verlauf hat,
gibt uns unsere geometrische Anschauung eine intuitive Vorstellung davon, was damit gemeint ist.
Wir führen sogleich eine Rede- und Schreibweise für dieses Konzept ein:
Wir bezeichnen den Inhalt der Fläche unter dem Graphen einer Funktion f
zwischen den Stellen a und b
als bestimmtes Integral und schreiben es in der Form
(ausgesprochen: "Integral f(x) in den Grenzen von a bis
b" oder "Integral f(x) dx
von a bis b", auch
"Integral über f(x) von a bis b").
Wie beim oben besprochenen unbestimmten Integral wird f(x) als
Integrand bezeichnet, a heißt untere
und b heißt obere Integrationsgrenze, und das Intervall
[a, b]
wird Integrationsbereich (auch Integrationsintervall oder Integrationsgebiet) genannt.
Das Symbol für die Integrationsvariable - in (7) wurde x verwendet -
kann dabei beliebig gewählt werden. So steht beispielsweise dx
von a bis b", auch
"Integral über f(x) von a bis b").
Wie beim oben besprochenen unbestimmten Integral wird f(x) als
Integrand bezeichnet, a heißt untere
und b heißt obere Integrationsgrenze, und das Intervall
[a, b]
wird Integrationsbereich (auch Integrationsintervall oder Integrationsgebiet) genannt.
Das Symbol für die Integrationsvariable - in (7) wurde x verwendet -
kann dabei beliebig gewählt werden. So steht beispielsweise
| b |
|
|
b |
|
| ò |
f(x) dx |
oder |
ò |
f(x') dx' |
| a |
|
|
a |
|
|
(7' ) |
für dieselbe Zahl wie (7).
Sie werden sich jetzt vielleicht fragen, wieso für Flächeninhalte eine ähnliche Schreibweise
wie für Stammfunktionen verwendet wird. Ihre Frage ist berechtigt und führt auf einen der
faszinierendsten Zusammenhänge der modernen Mathematik:
Der Hauptsatz
Ist f stetig, so ist der Flächeinhalt unter dem Graphen von f
eng mit der Stammfunktion von f
verwandt. Um das einzusehen, definieren wir eine Funktion A, deren Werte
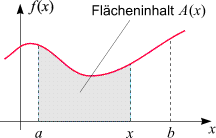 Flächeninhalte sind:
A(x) sei die Fläche
unter dem Graphen von f
zwischen der (festgehaltenen) Untergrenze a
und einer (variablen) Obergrenze x
im Intervall
[a, b],
d.h. das bestimmte Integral über f in den Grenzen von
a bis x.
Wir können A eine
Flächenfunktion nennen. Die Fläche zwischen
a und
b, d.h. das bestimmte
Integral (7), ergibt sich dann
als Funktionswert A(b).
Flächeninhalte sind:
A(x) sei die Fläche
unter dem Graphen von f
zwischen der (festgehaltenen) Untergrenze a
und einer (variablen) Obergrenze x
im Intervall
[a, b],
d.h. das bestimmte Integral über f in den Grenzen von
a bis x.
Wir können A eine
Flächenfunktion nennen. Die Fläche zwischen
a und
b, d.h. das bestimmte
Integral (7), ergibt sich dann
als Funktionswert A(b).
Wir untersuchen nun, wie sich A(x)
unter einer kleinen Änderung von x
verhält:
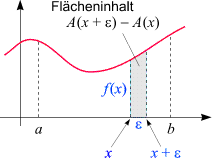 Ändern wir x auf
x + e,
so ändert sich der Funktionswert von A(x)
auf A(x + e).
Die Differenz
A(x + e) - A(x)
hat eine einfache Bedeutung: Da in ihr die Fläche unter dem Graphen zwischen
a und x
zweimal mit jeweils unterschiedlichem Vorzeichen eingeht und daher wieder herausfällt,
bleibt der Flächeninhalt des Streifens zwischen
x und
x + e
übrig.
Ändern wir x auf
x + e,
so ändert sich der Funktionswert von A(x)
auf A(x + e).
Die Differenz
A(x + e) - A(x)
hat eine einfache Bedeutung: Da in ihr die Fläche unter dem Graphen zwischen
a und x
zweimal mit jeweils unterschiedlichem Vorzeichen eingeht und daher wieder herausfällt,
bleibt der Flächeninhalt des Streifens zwischen
x und
x + e
übrig.
Ist e sehr klein, so ist dieser Streifen sehr schmal.
Da f laut Voraussetzung stetig ist, sind alle Funktionswerte innerhalb des
Intervalls [x, x + e]
ungefähr gleich groß (und werden einander immer ähnlicher, je kleiner e ist).
Der Flächeninhalt des Streifens kann daher durch jenen eines Rechtecks mit Seitenlängen
e und f(x)
approximiert werden.
Auf diese Weise gelangen wir zur Abschätzung
| | | |

stetig
*
stückweise stetig
| |
| | |
für kleines e. Je kleiner e ist,
umso genauer gilt diese Näherungsformel. Nun kommt ein kleiner Rechenschritt mit
großen Konsequenzen: Wir dividieren beide Seiten durch e und bilden den Grenzwert für
e ® 0,
| |
|
A(x
+ e) - A(x)
e |
=
f(x) , |
| lim |
| e ® 0 |
|
(9) |
| | | |

Grenzwert einer Funktion
| |
| | |
in dem die in (8) für
e ¹ 0 noch vorhandene Ungenauigkeit verschwunden ist.
Auf der linken Seite steht nichts anderes als die Ableitung von
A(x):
Die Ableitung (d.h. die Änderungsrate) der Flächenfunktion ist nichts anderes als die gegebene Funktion
f.
Mit anderen Worten: Ist f stetig,
so ist die Flächenfunktion A
eine Stammfunktion von f.
Damit sind wir mit einem Schlag in die Lage versetzt, die Inhalte von Flächen, die von Kurven begrenzt werden,
berechnen zu können - sofern wir es schaffen, die
dazu benötigten Stammfunktionen zu ermitteln:
Angenommen, wir kennen eine Stammfunktion F von
f.
Dann unterscheiden sich A und
F
gemäß unserer obigen Erkenntnis (2) höchstens durch eine Konstante,
so dass A(x) = F(x) + c.
Da A(a) = 0 ist, folgt
c = -F(a),
und die gesuchte Fläche A(b) ist daher gleich
A(b) = F(b) + c =
F(b) - F(a).
Für ihre Berechnung müssen wir lediglich irgendeine Stammfunktion von
f kennen und die Differenz ihrer Werte an
den Stellen b und a
bilden. Für diese Differenz hat sich die Schreibweise
bzw. die etwas genauere Form
| |
| |
x = = b b |
|
| F(x) |
|
º F(b)
- F(a) |
| |
x = = a a |
|
|
(11' ) |
eingebürgert.
Mit Hilfe der Bezeichnungsweise (7) können wir unser Resultat über die Flächenberechnung
für stetiges f in der Form
| b |
|
| |
b |
|
| ò |
f(x) dx
= F(x) |
|
º F(b)
- F(a) |
| a |
|
a |
|
|
(12) |
schreiben, wobei
F
irgendeine Stammfunktion von f ist.
Es ist so bedeutend, dass es den Namen Hauptsatz der Differential- und Integralrechnung
bekommen hat.
| | | |
Genauere
| |
| | |
Probieren
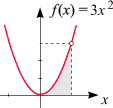 wir das gleich anhand eines Beispiels aus: Das unbestimmte Integral der Funktion
f(x) = 3x2
haben wir bereits oben in (4) hingeschrieben: Um irgend eine Stammfunktion zu erhalten,
können wir die Konstante c
ignorieren und wählen
F(x) = x3.
Die Fläche unter dem Graphen von f
(der, wie wir ja wissen, eine Parabel darstellt) zwischen den Stellen
0 und 1
ist daher
wir das gleich anhand eines Beispiels aus: Das unbestimmte Integral der Funktion
f(x) = 3x2
haben wir bereits oben in (4) hingeschrieben: Um irgend eine Stammfunktion zu erhalten,
können wir die Konstante c
ignorieren und wählen
F(x) = x3.
Die Fläche unter dem Graphen von f
(der, wie wir ja wissen, eine Parabel darstellt) zwischen den Stellen
0 und 1
ist daher
| 1 |
|
| |
1 |
|
| ò |
3x2 dx
= x3 |
|
= 13 - 03 = 1. |
| 0 |
|
0 |
|
|
Wer hätte gedacht, dass es so einfach ist, die Fläche unter einer Parabel zu berechnen?
| | | |

Parabel
(in Vorbereitung)
| |
| | |
Einige Bemerkungen zum bestimmten Integral
- Wir
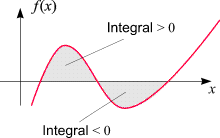 haben bisher, ohne es genau auszusprechen, nur an Funktionen gedacht, die positive Funktionswerte besitzen, d.h. deren Graphen
oberhalb der x-Achse liegen. Wir lassen nun diese Einschränkung fallen
und legen fest, dass das bestimmte Integral (7) den orientierten Flächeninhalt darstellt
(siehe dazu auch den nebenstehenden Button), d.h. dass Flächenstücke
unterhalb der x-Achse
(oberhalb des Graphen von f ) mit negativem
Vorzeichen beitragen! Wird ein bestimmtes Integral mit Hilfe des Hauptsatzes
(12) berechnet, so wird diese Regel automatisch berücksichtigt.
haben bisher, ohne es genau auszusprechen, nur an Funktionen gedacht, die positive Funktionswerte besitzen, d.h. deren Graphen
oberhalb der x-Achse liegen. Wir lassen nun diese Einschränkung fallen
und legen fest, dass das bestimmte Integral (7) den orientierten Flächeninhalt darstellt
(siehe dazu auch den nebenstehenden Button), d.h. dass Flächenstücke
unterhalb der x-Achse
(oberhalb des Graphen von f ) mit negativem
Vorzeichen beitragen! Wird ein bestimmtes Integral mit Hilfe des Hauptsatzes
(12) berechnet, so wird diese Regel automatisch berücksichtigt.
Beispiel:
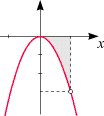 Der Graph der Funktion f(x) = -3x2
ist eine Parabel unterhalb der x-Achse, und dementsprechend ist das Integral
Der Graph der Funktion f(x) = -3x2
ist eine Parabel unterhalb der x-Achse, und dementsprechend ist das Integral
| 1 |
|
| |
1 |
|
| ò |
(-3x2) dx
= - x3 x3 |
|
= - (13 - 03) = -1 (13 - 03) = -1 |
| 0 |
|
0 |
|
|
negativ.
Ist das Integral einer Funktion über ein gegebenes Intervall gleich
0, so sind in diesem Intervall die Flächen oberhalb und
unterhalb der x-Achse gleich groß, so daß ihre
Inhalte einander wegheben.
| | | |
Flächeninhalt
| |
| | |
- Das bestimmte Integral als "orientierter Flächeninhalt" hat eine weitere Konsequenz:
Man möchte zunächst meinen, dass (7) nur dann einen Sinn macht, wenn die untere
Integrationsgrenze kleiner ist als die obere, d.h. wenn
a < b gilt.
Es hat sich jedoch als zweckmäßig herausgestellt, diese Einschränkung fallen zu lassen,
d.h. bestimmte Integrale mit beliebigen Grenzen zu erlauben, und die Rechenregel
| a |
|
b |
|
| ò |
f(x) dx
= -
|
ò |
f(x) dx
|
| b |
|
a |
|
|
(13) |
aufzustellen: Das Vertauschen der Grenzen ändert das Vorzeichen.
Wird ein bestimmtes Integral mit Hilfe des Hauptsatzes
(12) berechnet, so wird auch diese Regel automatisch berücksichtigt.
In diesem Fall tragen die Flächenstücke oberhalb der x-Achse
mit negativem Vorzeichen, jene unterhalb der x-Achse
mit positivem Vorzeichen bei.
- Das bestimmte Integral kann auch als kontinuierliche Verallgemeinerung des Mittelwerts
und der Summe interpretiert werden. Näheres dazu ruft der nebenstehende Button auf.
| | | |
Integral als
| |
| | |
- Bei der Herleitung des
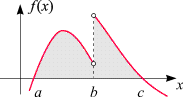 Hauptsatzes (12) haben wir vorausgesetzt, dass f
stetig ist. Das bedeutet aber nicht, dass nur stetige Funktionen integriert werden können.
Soll das bestimmte Integral einer stückweise stetigen Funktion mit Hilfe von (12) berechnet werden,
so muss jedes Intervall, in dem sie stetig ist, für sich betrachtet werden. Danach wird die Summe dieser
Einzelintegrale addiert. (In der nebenstehende Skizze wären die Integrale
von a bis b
und von b bis c
getrennt zu berechnen und danach zu addieren).
Hauptsatzes (12) haben wir vorausgesetzt, dass f
stetig ist. Das bedeutet aber nicht, dass nur stetige Funktionen integriert werden können.
Soll das bestimmte Integral einer stückweise stetigen Funktion mit Hilfe von (12) berechnet werden,
so muss jedes Intervall, in dem sie stetig ist, für sich betrachtet werden. Danach wird die Summe dieser
Einzelintegrale addiert. (In der nebenstehende Skizze wären die Integrale
von a bis b
und von b bis c
getrennt zu berechnen und danach zu addieren).
- Wie wir weiter unten im Abschnitt über "uneigentliche Integrale" besprechen werden, können die Integrationsgrenzen unter gewissen Voraussetzungen
durch -¥ oder ¥
ersetzt werden, und an einer (endlichen) Integrationsgrenze darf f
eine (genügend milde) Unendlichkeitsstelle besitzen. Damit können die Inhalte von Flächen berechnet werden,
die "bis ins Unendliche" reichen.
| | | |

stückweise stetig
| |
| | |
- Zur Bedeutung der in (3) und (7) verwendeten Symbole
ò und dx:
Diese Schreibweise stammt von Gottfried Wilhelm von Leibniz. Er hat sich die Fläche unter einem
Funktionsgraphen als aus unendlich vielen, unendlich dünnen nebeneinander stehenden Rechtecken zusammengesetzt gedacht,
jedes ähnlich dem schmalen Streifen, den wir in (8) betrachtet haben. Wird in (8)
e = dx
gesetzt und als unendlich kleine ("infinitesimale") Größe, als "Differential", aufgefasst, so stellt sich der
Flächeninhalt als "Summe" von unendlich vielen unendlich kleinen Rechtecksflächen
f(x)
 dx
dar. Das Integralzeichen, als langgestrecktes "S", steht für diese "Summe". Sie erstreckt sich
in gewisser Weise "über alle x",
beginnend bei a und endend bei b,
was oberhalb und unterhalb des Integralzeichens vermerkt wird. In dieser Interpretation ist die Größe
f(x) dx
dar. Das Integralzeichen, als langgestrecktes "S", steht für diese "Summe". Sie erstreckt sich
in gewisser Weise "über alle x",
beginnend bei a und endend bei b,
was oberhalb und unterhalb des Integralzeichens vermerkt wird. In dieser Interpretation ist die Größe
f(x) dx,
wie die Schreibweise nahelegt, tatsächlich
ein Produkt. Die "infinitesimale" Sichtweise ist heute überholt (die Schreibweise nur mehr symbolisch zu verstehen),
die ihr zugrunde liegende Vorstellung kann durch einen wohldefinierten Grenzübergang ersetzt werden,
aber sie ist nach wie vor hilfreich und regt die Anschauung an.
Auf die Möglichkeiten, den Integralbegriff exakter zu fassen, werden wir weiter unten noch
zu sprechen kommen. dx,
wie die Schreibweise nahelegt, tatsächlich
ein Produkt. Die "infinitesimale" Sichtweise ist heute überholt (die Schreibweise nur mehr symbolisch zu verstehen),
die ihr zugrunde liegende Vorstellung kann durch einen wohldefinierten Grenzübergang ersetzt werden,
aber sie ist nach wie vor hilfreich und regt die Anschauung an.
Auf die Möglichkeiten, den Integralbegriff exakter zu fassen, werden wir weiter unten noch
zu sprechen kommen.
Damit wissen Sie die wichtigsten Dinge, die nötig sind, um konkrete Flächeninhalte zu berechnen. Betrachten wir
zum Abschluss dieses Abschnitts zwei Beispiele, um die konkrete Vorgangsweise bei Flächenberechnungen zu illustrieren:
Beispiel 1: Man berechne die Fläche unter dem Graphen der Funktion
f(x) = x2 - 1
zwischen den Stellen 1 und 2.
Eine Stammfunktion der gegebenen Funktion ist, wie sich leicht herausfinden lässt,
F(x) = x3/3 - x.
Nachdem wir das nun wissen (das Auffinden einer Stammfunktion ist in der Regel der schwierigste Teil einer Integrationsaufgabe),
besteht die Lösung der Aufgabe aus zwei Schritten:
-
Um sicherzugehen, dass keine Weghebungen von Flächenstücken oberhalb und unterhalb der
x-Achse passieren können,
müssen wir uns erst vergewissern, dass die Funktion f
im angegebenen Intervall
[1, 2]
nicht negativ werden kann. Das geschieht durch die Berechnung der Nullstellen oder, wenn man sich eine kleine
Nachlässigkeit gönnt, durch die Betrachtung des Graphen, z.B. mit dem Funktions-Plotter
(am besten aber durch beides). Prüfen Sie das für unser Beispiel selbständig nach!
-
Der Rest der Rechnung läuft im Grunde genommen ganz mechanisch ab:
| 2 |
|
| |
2 |
|
| ò |
(x2
- 1) dx
= (x3/3 -
x) |
|
= |
| 1 |
|
1 |
|
|
| |
|
= (23/3 -
2) - (13/3 -
1) = 4/3 . |
| |
|
Der gesuchte Flächeninhalt ist 4/3.
| | | |

infinitesimal
| |
| | |
Beispiel 2: Man berechne die Fläche unter dem Graphen der Funktion f(x) = 1/x
zwischen den Stellen 1 und s > 0.
Eine Stammfunktion von 1/x ist der
natürliche Logarithmus ln x.
Das ergibt sich ganz einfach aus
(ln x)' = 1/x.
Da
ln(1) = 0 ist,
lautet die Antwort
ln s.
Diese Erkenntnis wird manchmal dazu benutzt, die Argumentation umzukehren und den natürlichen Logarithmus über die Beziehung
zu definieren. (Beachten Sie, dass die Integrationsvariable hier mit einem anderen Buchstaben
als x, der oberen Grenze, bezeichnet wird).
Diese Definition hat den Vorteil, dass sie kurz ist und - sofern der Integralbegriff
als bekannt vorausgesetzt werden darf - keinerlei Vorbereitungen
über Potenzen mit nicht-ganzzahligen Exponenten und über die
Eulersche Zahl e bedarf.
Der Rest dieses Kapitels dient der näheren Besprechung der Vorgangsweise beim Integrieren,
der Zusammenstellung von Rechenregeln und der Vertiefung des bisher
Gesagten.
|
| | |

Ableitung des Logarithmus

frühere Definition des Logarithmus

die Eulersche Zahl e
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Beim Differenzieren haben wir eine Reihe einfacher Rechenregeln kennengelernt, die es erlaubt hat,
die Ableitung einer Kombination von Funktionen (wie Produkt, Quotient und Verkettung) auf
jene ihrer Bestandteile zurückzuführen. Beim Integrieren ist das leider nicht so.
In der Integralrechnung besteht keine Garantie, dass ein gestelltes Problem, auch wenn es
einfach aussieht, eine einfache Lösung hat. Daher können auch Computerwerkzeuge,
auf die wir weiter unten zu sprechen kommen, zwar oft, aber nicht
immer helfen.
Wir stellen nun einige Integrationsregeln und Methoden zusammen, die beim Auffinden der Stammfunktion und der Auswertung bestimmter
Integrale hilfreich sind und geben anschließend ein paar praktische Tipps.
1.) Zusammenhang zwischen bestimmtem und unbestimmtem Integral und Varianten des Hauptsatzes:
| | | |

Ableitungsregeln
| |
| | |
Ist f eine stetige Funktion, so ist
eine Stammfunktion (d.h. ein unbestimmtes Integral) von f, wobei die
Stelle a beliebig gewählt werden kann.
Das folgt unmittelbar daraus, dass F eine
Flächenfunktion darstellt (wir haben sie im vorigen Abschnitt
A genannt) und aus unserem obigen Ergebnis (10).
Beachten Sie die Schreibweise in (15): Man vermeidet es, die Integrationsvariable
mit dem gleichen Symbol zu bezeichnen wie eine Integrationsgrenze.
Das unbestimmte Integral lässt sich also als bestimmtes Integral (mit unbestimmter unterer Grenze)
darstellen. Die Aussage
F '(x) = f(x)
kann auch in der Form
d
dx |
|
x |
|
| |
ò |
f(x') dx' = f(x)
|
| |
a |
|
|
(16) |
geschrieben werden. In Worten lautet sie: Die Ableitung eines bestimmten Integrals nach der oberen Integrationsgrenze ergibt den
Integranden. Das ist eine Möglichkeit, die Idee des Integrierens als "Umkehrung des Differenzierens" durch eine Formel auszudrücken.
Eine andere ergibt sich, indem wir (12) in der Form
| b |
|
| ò |
F '(x) dx
= F(b) -
F(a) |
| a |
|
|
(17) |
| | | |
| |
| | |
schreiben, die für jede differenzierbare Funktion F gilt.
In Worten: Das bestimmte Integral über eine Ableitung ergibt die Differenz der Funktionswerte des Integranden an den Integrationsgrenzen.
Sowohl (16) als auch (17) können als Varianten des
Hauptsatzes (12) angesehen werden. Letzte Beziehung stellt in kompakter Form
dar, was wir tun müssen, um ein bestimmtes Integral zu berechen: Man finde eine Funktion,
deren Ableitung der Integrand ist, und bilde die Differenz ihrer Werte an den Integrationsgrenzen.
| | | |

differenzierbar
| |
| | |
Zum Verständnis des Integrals und zur Festigung der Intuition über diesen Begriff ist es lehrreich, sich
einige Zusammenhänge zwischen den Funktionen f
und F zu verdeutlichen.
So verschwindet etwa die Ableitung von F genau
an den Nullstellen von f. Wechselt
f an einer solchen Nullstelle das Vorzeichen,
so besitzt F dort ein lokales Extremum.
Das nebenstehende Applet erlaubt es Ihnen, mit der Maus eigene Funktionsverläufe von
f hervorzuzaubern, sich davon zu überzeugen,
wie sich gewisse Eigenschaften von f in
jenen von F widerspiegeln,
und mit diesen Zusammenhängen ein bisschen zu experimentieren.
2.) Integral eines Vielfachen:
| | | |
Applet
Das Integral intuitiv verstehen
| |
| | |
Ist c eine Konstante und F
eine Stammfunktion von f, so ist
c F
eine Stammfunktion von
c F
eine Stammfunktion von
c f.
In Worten: Die Stammfunktion eines Vielfachen ist das Vielfache der Stammfunktion. f.
In Worten: Die Stammfunktion eines Vielfachen ist das Vielfache der Stammfunktion.
Beweis:
(c F(x))' =
c F(x))' =
c F '(x) =
c F '(x) =
c f(x). f(x).
Diese Regel überträgt sich auf bestimmte Integrale in der Form
| b |
|
b |
|
| ò |
c f(x) dx
= c |
ò |
f(x) dx, |
| a |
|
a |
|
|
(18) |
in der die Stetigkeit von f übrigens nicht vorausgesetzt werden muss.
Von der geometrischen Anschauung her ist sie leicht verständlich: Der Flächeninhalt unter
dem Graphen einer mit dem Faktor c
multiplizierten Funktion ist gleich dem c-fachen
des ursprünglichen Flächeninhalts. Für das praktische Rechnen bedeutet sie:
Eine Konstante darf aus einem Integral herausgezogen werden.
3.) Integral einer Summe:
| | | |
| |
| | |
Ist F eine Stammfunktion von f und
G eine Stammfunktion von g, so ist
F + G
eine Stammfunktion von f + g.
In Worten: Die Stammfunktion einer Summe ist die Summe der Stammfunktionen.
Beweis:
(F(x) + G(x))' =
F '(x) + G '(x) =
f(x) + g(x).
Diese Regel überträgt sich auf bestimmte Integrale in der Form
| b |
|
b |
|
b |
|
| ò |
( f(x)
+ g(x )) dx
= )) dx
= |
ò |
f(x) dx
+ |
ò |
g(x) dx, |
| a |
|
a |
|
a |
|
|
(19) |
in der die Stetigkeit von f und g nicht vorausgesetzt werden muss.
Von der geometrischen Anschauung her ist sie leicht verständlich: Der Flächeninhalt unter
dem Graphen einer Summe zweier Funktionen ist gleich der Summe der
Flächeninhalte unter den Graphen der Summanden. Für das praktische Rechnen bedeutet sie:
Eine Summe von bestimmten Integralen mit denselben Integrationsgrenzen kann zu einem Integral zusammengezogen werden.
Die beiden Regeln (18) und (19) zusammen drücken die Tatsache aus, dass
das Integrieren eine "lineare Operation" ist.
4.) Integration über angrenzende Intervalle:
| | | |
| |
| | |
Wird ein und dieselbe Funktion f über zwei angrenzende Intervalle integriert,
so ist die Summe dieser beiden Integrale gleich dem Integral über die Vereinigung der beiden
Intervalle:
| b |
|
c |
|
c |
|
| ò |
f(x) dx
+ |
ò |
f(x) dx
= |
ò |
f(x) dx . |
| a |
|
b |
|
a |
|
|
(20) |
Auch für diese Regel muss die Stetigkeit des Integranden nicht vorausgesetzt werden.
Von der geometrischen Anschauung her ist sie leicht verständlich: Der Inhalt einer
Fläche, die sich aus zwei Stücken zusammensetzt, ist gleich der Summe der einzelnen
Flächeninhalte. Sie gilt übrigens auch dann, wenn nicht unbedingt
a £ b £ c
ist. Wir erinnern in diesem Zusammenhang an die Rechenregel (13).
5.) Lineare Transformationen des Arguments:
| | | |
| |
| | |
Ist F(x) eine
Stammfunktion von f(x), so
- ist F(x + a) eine Stammfunktion von
f(x + a) und
- k-1F(kx) eine Stammfunktion von
f(kx).
Zum Beweis differenzieren Sie einfach die angegebenen Stammfunktionen!
Damit ergeben sich beispielsweise die unbestimmten Integrale von
sin(x + a)
und ekx
sofort aus jenen von
sin x
und ex zu
- cos(x + a)
und k-1ekx. cos(x + a)
und k-1ekx.
6.) Partielle Integration:
| | | |
| |
| | |
Ist F eine Stammfunktion von f und
g differenzierbar, so ist das unbestimmte Integral
des Produkts f g
durch
| ò |
f(x) g(x) dx
= F(x) g(x) - |
ò |
F(x) g'(x) dx |
|
(21) |
gegeben. Diese Formel erinnert ein bisschen an die Produktregel für die Ableitung, stammt auch von dieser ab, hat aber eine
kompliziertere Struktur. Der wichtigste Schritt besteht darin, von einem der beiden Faktoren
( f ) die Stammfunktion,
vom anderen (g) die Ableitung zu bilden,
um zum Integral auf der rechten Seite zu gelangen. Leider ist durch nichts
garantiert, dass dieses einfacher zu berechnen ist als das auf der linken.
Immerhin ist das manchmal der Fall, und so gehört die Methode der partiellen Integration
zum Standardrepertoire der Integralrechnung.
| | | |

Produktregel
| |
| | |
Als Beispiel berechnen wir das unbestimmte Integral des natürlichen Logarithmus. Dazu verwenden wir die
Tatsache, dass
(ln x)' = 1/x
ist und wenden einen genialen Trick an: Der Integrand
ln x wird in der Form
1 × ln x
geschrieben, und Formel (21) wird mit
f(x) = 1 und
g(x) = ln x
angewandt. Eine Stammfunktion von 1 ist
x, womit sich
F(x) = x und
g'(x) = 1/x ergibt.
Simples Einsetzen in (21) liefert
| ò |
ln x dx
= |
x ln x - |
ò |
dx
= x ln x - x, |
|
(22) |
wobei wir für
ò 1 1 dx
einfach
ò dx
einfach
ò dx
geschrieben haben. Überprüfen Sie dieses Resultat durch Differenzieren
(d.h. checken Sie, dass die Ableitung von
x ln x - x
gleich
ln x
ist)! dx
geschrieben haben. Überprüfen Sie dieses Resultat durch Differenzieren
(d.h. checken Sie, dass die Ableitung von
x ln x - x
gleich
ln x
ist)!
Wenn Sie diese Methode für andere Integrale üben wollen, benutzen Sie sie, um
ò x x sin sin x x dx,
ò dx,
ò x x cos cos x x dx,
ò dx,
ò x2 x2 sin sin x x dx und
ò dx und
ò x2 x2 cos cos x x dx zu berechnen.
(Erinnern Sie sich: Die Stammfunktionen von
sin dx zu berechnen.
(Erinnern Sie sich: Die Stammfunktionen von
sin x und
cos x und
cos x
sind
- x
sind
- cos cos x und
sin x und
sin x,
die Ableitungen von
x und x2
sind
1 und 2x).
Integrale dieser Art werden in der Theorie der Fourierreihen benötigt. x,
die Ableitungen von
x und x2
sind
1 und 2x).
Integrale dieser Art werden in der Theorie der Fourierreihen benötigt.
| | | |

Fourierreihen
| |
| | |
Für bestimmte Integrale nimmt Regel (21) die Form
| b |
|
| |
b |
|
b |
|
| ò |
f(x) g(x) dx
= F(x) g(x) |
|
- |
ò |
F(x) g'(x) dx |
| a |
|
a |
|
a |
|
|
(23) |
an.
7.) Substitutionsmethode (Variablensubstitution, Variablentransformation):
| | | |
| |
| | |
Manchmal ist es günstig, beim Berechnen eines Integrals die Variable als Funktion einer anderen
Größe u aufzufassen.
Wir schreiben diese Abhängigkeit als x º x(u),
verlangen, dass die dadurch definierte Funktion differenzierbar ist und schreiben deren Ableitung
als x'(u)
oder dx(u)/du.
Weiters soll es sich um eine umkehrbare Zuordnung (eine bijektive Funktion) handeln, d.h. es soll auch möglich sein,
u durch x
auszudrücken, was wir einfach als u º u(x)
schreiben.
Dann ist das bestimmte Integral von f durch
| ò |
f(x) dx
=
|
ò |
f(x(u)) x'(u) du |
|
(24) |
| | | |

bijektiv
| |
| | |
gegeben, wobei auf der rechten Seite nach der Berechnung u
durch u(x) zu ersetzen ist.
Dadurch entsteht ein neuer Integrand, für den die weitere Berechnung leichter sein kann.
Diese Identität stammt von der Kettenregel ab.
Für bestimmte Integrale nimmt sie die Form
| x2 |
|
u2 |
|
| ò |
f(x) dx
=
|
ò |
f(x(u)) x'(u) du |
| x1 |
|
u1 |
|
|
(25) |
an, wobei die Grenzen x1 und
u1
(sowie x2 und
u2) einander entsprechende
Werte sind
(d.h. u1 = u(x1)
und u2 = u(x2)
oder, was dasselbe bedeutet,
x1 = x(u1)
und x2 = x(u2)).
Eine andere Form, (25) auszudrücken, ist
| x2 |
|
u2 |
|
| ò |
f(x) dx
=
|
ò |
f(x(u)) |
dx(u)
du |
du . |
| x1 |
|
u1 |
|
|
(25' ) |
| | | |

Kettelregel
| |
| | |
Die Grundstruktur dieser Formel kann man sich leicht merken:
Die Regel besteht im Wesentlichen darin, unter dem Integral den Bruch
1 = du/du
einzuschieben und den "Quotienten"
dx/du
als Ableitung, d.h.
dx(u)/du,
zu interpretieren. Der Rest besteht dann nur darin, u
anstelle von x als neue Integrationsvariable
aufzufassen und die Grenzen entsprechend anzupassen.
Das ist ein schönes Beispiel dafür, wie die Deutung der Symbole dx
und du als "Differentiale" die
Intuition anspricht.
Die Substitution ( = = "Ersetzung")
der Integrationsvariable durch eine andere ist eine wichtige Integrationstechnik.
Betrachten wir ein "Ersetzung")
der Integrationsvariable durch eine andere ist eine wichtige Integrationstechnik.
Betrachten wir ein
Beispiel: Wir wollen das unbestimmte Integral von
4x sin(x2)
ermitteln. Dazu verwenden wir die neue Variable
u = x2 (oder,
was dasselbe bedeutet, x = u1/2).
Solange x ³ 0
und u ³ 0 ist, besteht eine
umkehrbare Entsprechung zwischen x und u.
Um die Substitution auszuführen, berechnen wir x'(u) º
dx/du =
(1/2) × u-1/2, formen um zu
dx =
u-1/2du/2
und setzen in das unbestimmte Integral ein, womit sich folgende Rechnung ergibt: sin(x2)
ermitteln. Dazu verwenden wir die neue Variable
u = x2 (oder,
was dasselbe bedeutet, x = u1/2).
Solange x ³ 0
und u ³ 0 ist, besteht eine
umkehrbare Entsprechung zwischen x und u.
Um die Substitution auszuführen, berechnen wir x'(u) º
dx/du =
(1/2) × u-1/2, formen um zu
dx =
u-1/2du/2
und setzen in das unbestimmte Integral ein, womit sich folgende Rechnung ergibt:
| ò |
4x sin(x2) dx
= sin(x2) dx
=
|
ò |
4u1/2 sin u u-1/2
du/2
= sin u u-1/2
du/2
=
|
|
(26) |
| = |
ò |
2 sin u du = -2 sin u du = -2 cos u = -2 cos u = -2 cos(x2) . cos(x2) . |
|
Wir hätten statt dessen auch damit beginnen können, die Ableitung der inversen Funktion
u'(x) º
du/dx =
2x zu berechnen (damit sparen wir uns die halbzahligen Exponenten) und zu
dx =
du/(2x) umzuformen.
Durch Differenzieren überzeugt man sich übrigens, dass dieses Resultat für alle
x
(nicht nur für x ³ 0)
gilt.
Anmerkung: Der letzte Schritt in (26), das "Rücksubstituieren",
also das Ersetzen von u durch
x2, damit das Resultat in der
ursprünglichen Variablen ausgedrückt ist, darf nicht vergessen werden!
Welche neue Variable für ein gegebenes Integral die günstigste ist, ergibt
sich manchmal erst nach ein paar Versuchen. Unter Umständen muss man das nach einer Substitution erhaltene Integral
mit einer weiteren Substitution bearbeiten, um zu einer Lösung zu kommen.
Wenn Sie viele derartige
Aufgaben rechnen (müssen), werden Sie einen gewissen Blick dafür entwickeln.
Beweisen Sie als Übungsaufgabe die beiden Aussagen der obigen Regel 5
unter Anwendung von (24) mit geeigneten neuen Variablen!
8.) Partialbruchzerlegung:
| | | |

Differential
| |
| | |
Dabei handelt es sich um eine Methode, den Term einer rationalen Funktion (d.h. des Quotienten zweier
Polynome) in einer systematischen Weise so umzuschreiben,
dass seine Stammfunktion ermittelt werden kann. Dank der Existenz dieser Methode kann die Integration rationaler Funktionen
zuverlässig vom Computer übernommen werden. Wir erläutern sie lediglich anhand eines Beispiels
(siehe nebenstehenden Button).
Ein Online-Werkzeug, das die Partialbruchzerlegung auf Funktionen Ihrer Wahl anwendet,
werden wir weiter unten angeben.
Integrale spezieller Funktionen
Da es für das Integrieren keine so bequemen Regeln wie für das Differenzieren gibt,
sind Integrationstabellen ( = Integraltafeln = Auflistungen von Integralen) in der Regel wesentlich umfangreicher als
Ableitungstabellen. Auf eine umfangreiche Liste von Integralen wollen wir
- auch angesichts der unten zu besprechenden
Computerwerkzeuge - verzichten.
Der folgende Button ruft eine ausgewählte Liste von Stammfunktionen
und einige bestimmte Integrale auf:
Alle angegebenen Stammfunktionen können durch Differenzieren überprüft werden.
Unter den bestimmten Integralen finden sich auch uneigentliche (siehe unten),
deren Herleitung zum Teil schwieriger ist.
Bemerkung: Auch wenn Sie umfangreichere Integrationstabellen als diese
(oder elektronische Hilfen, s.u.) verwenden, werden Sie das eine oder andere
Integral vermissen. Zwar besitzt jede stetige Funktion eine Stammfunktion. Das bedeutet aber nicht,
dass diese in einer einfachen Weise dargestellt werden kann.
Von manchen Funktionen läßt sich (im Rahmen einer Theorie, auf die wir nicht eingehen) beweisen, dass ihre
Stammfunktionen nicht durch elementare Funktionen (Potenzen, Winkelfunktionen, Exponential- und Logarithmusfunktionen
und beliebige Kombinationen dieser mit Hilfe der Grundrechnungsarten) in Form eines "geschlossenen" Ausdrucks angegeben werden können.
Solche Funktionen nennt man nicht geschlossen integrierbar.
Beispiele dafür sind
(sin x)/x,
ex2 und
e-x2.
Wird die Stammfunktion einer solcher Funktion oft benötigt, so erhält sie in der Regel
einen eigenen Namen, z.B. Integralsinus für das erste und (Gaußsche) Fehlerfunktion
(englisch error function) für das dritte dieser Beispiele.
Auch wenn eine Funktion nicht geschlossen integrierbar ist, kann ihr bestimmtes Integral (für ausgewählte Grenzen)
durchaus wieder eine "schöne" Darstellung besitzen, vgl. etwa (31) unten. x)/x,
ex2 und
e-x2.
Wird die Stammfunktion einer solcher Funktion oft benötigt, so erhält sie in der Regel
einen eigenen Namen, z.B. Integralsinus für das erste und (Gaußsche) Fehlerfunktion
(englisch error function) für das dritte dieser Beispiele.
Auch wenn eine Funktion nicht geschlossen integrierbar ist, kann ihr bestimmtes Integral (für ausgewählte Grenzen)
durchaus wieder eine "schöne" Darstellung besitzen, vgl. etwa (31) unten.
| | | |

rationale Funktion
| |
| | |
Praktische Tipps für die Suche nach der Stammfunktion
- Die Stammfunktionen mancher einfacher Funktionen lassen sich mit ein bisscher Erinnerung
an das Differenzieren und an die Ableitungen spezieller Funktionen leicht erraten, andere werden
Sie in der soeben vorgestellten Tabelle finden.
Für lineare Kombinationen (Vielfache und Summen) beachten Sie die obigen Regeln 2
und 3.
- Bei Funktionen, die zusätzliche Konstante enthalten, wie etwa
sin(x + a),
ekx
und (1 + a2x2)-1,
hilft manchmal die obige Regel 5 weiter.
- Integrieren heißt probieren und improvisieren. Das gilt insbesondere dann, wenn Sie
Stammfunktionen bestimmen und die benutzen Methoden dokumentieren sollen.
Welche Methode schließlich zum Ziel führt, ist oft erst klar, wenn Sie die
gesuchte Stammfunktion gefunden haben. Wenn Sie viel mit Integralrechnung zu tun haben,
werden Sie mit der Zeit ein gewisses Gefühl dafür entwickeln.
- In einer bestimmten Hinsicht kann Integrieren sehr einfach sein: Durch Differenzieren läßt sich
leicht entscheiden, ob eine gegebene Funktion F
eine Stammfunktion der (auch gegebenen) Funktion f ist.
Nutzen Sie daher Integrationstabellen oder die unten zu besprechenden Computerwerkzeuge!
Auch wenn Sie daran interessiert sind, alle nötigen Rechnungen selbst durchzuführen,
können Sie den in einer Tabelle gefundenen oder von einem Computeralgebra-System
ausgegebenen Term für die Stammfunktion als Vorschlag betrachten.
Wenn Sie sich dann selbst davon überzeugen, dass dieser
tatsächlich eine Stammfunktion ist, behalten Sie die volle Kontrolle über die
Richtigkeit des Ergebnisses, können sich aber viel Arbeit ersparen.
Praktische Tipps für die Berechnung bestimmter Integrale
- Ist die Stammfunktion F von f
einmal gefunden, so ist das bestimmte Integral über f
in den Grenzen von a bis
b durch die Differenz
F(b) - F(a)
gegeben. Aber Vorsicht: Haben Sie einen Term für F
ermittelt, so könnte es passieren, dass zwischen den Stellen a und
b eine Singularität liegt. In diesem Fall ist die
durch den Term dargestellte Funktion nicht im gesamten Integrationsbereich differenzierbar, also
gar keine Stammfunktion!
Beispiel: Eine Stammfunktion von
1/x2
ist
-1/x.
Gilt daher
| 1 |
|
| |
1 |
|
| ò |
dx/x2
= -1/x |
|
= -1 -1 = -2 ? |
| -1 |
|
-1 |
|
|
(27) |
Nein! Sehen Sie sich den Graphen des Integranden an (z.B. mit dem Funktions-Plotter).
Tatsächlich hat die Fläche unter dem Graphen von
1/x2 zwischen
-1 und 1
einen unendlich großen Inhalt.
Und wieso hat die obige Rechnung ein falsches Ergebnis geliefert? Der Grund ist einfach:
-1/x
ist eine Stammfunktion von
1/x2
im Bereich x < 0
und im Bereich
x > 0,
nicht aber in einem Intervall, das die Stelle 0
enthält (denn dort sind beide Funktion gar nicht definiert).
Überprüfen Sie daher immer vor dem Einsetzen der Grenzen,
ob der Term für die Stammfunktion im Integrationsbereich Singularitäten besitzt. (Sehen Sie sich zumindest Plots von
Integrand und Term der Stammfunktion an!)
- Wenn Sie einen konkreten Flächeninhalt berechnen sollen, so beachten Sie, dass
Flächen unterhalb der x-Achse
mit negativem Vorzeichen zum Integral beitragen.
Beispiel: Sei
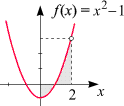 f(x) = x2 - 1.
Man berechne den Inhalt der im nebenstehenden Diagramm dargestellten Fläche.
Gesucht ist also die Summe der Inhalte der beiden Flächenstücke, von denen
eines oberhalb, eines unterhalb der x-Achse liegt.
Wenn Sie hier das bestimmte Integral der gegebenen Funktion in den Grenzen von
0 bis 2
berechnen, so erhalten Sie nicht den gesuchten Flächeninhalt, sondern
die Differenz der beiden Inhalte. Statt dessen müssen
die beiden Stücke zunächst getrennt behandelt werden:
Die (positive) Nullstelle unserer Funktion liegt bei x = 1, daher
bilden wir (die Details der Rechnung lassen wir Ihnen über)
f(x) = x2 - 1.
Man berechne den Inhalt der im nebenstehenden Diagramm dargestellten Fläche.
Gesucht ist also die Summe der Inhalte der beiden Flächenstücke, von denen
eines oberhalb, eines unterhalb der x-Achse liegt.
Wenn Sie hier das bestimmte Integral der gegebenen Funktion in den Grenzen von
0 bis 2
berechnen, so erhalten Sie nicht den gesuchten Flächeninhalt, sondern
die Differenz der beiden Inhalte. Statt dessen müssen
die beiden Stücke zunächst getrennt behandelt werden:
Die (positive) Nullstelle unserer Funktion liegt bei x = 1, daher
bilden wir (die Details der Rechnung lassen wir Ihnen über)
| 1 |
|
2 |
|
| ò |
(x
2 - 1) dx
= -2/3 und |
ò |
(x
2 - 1) dx
= 4/3. |
| 0 |
|
1 |
|
|
Die gesuchte Fläche ist daher
2/3 + 4/3 = 2, während das
bestimmte Integral von 0 bis 2
gleich -2/3 + 4/3 = 2/3 ist.
Orientieren Sie sich daher bei derartigen Aufgaben vor der Rechnung über die Lage der beteiligten Flächen
in Bezug auf die
x-Achse!
- In manchen Aufgaben ist der Inhalt einer Fläche zu berechnen, die zwischen zwei Funktionsgraphen liegt.
Flächeninhalte dieser Art lassen sich als Differenzen von
bestimmten Integralen ermitteln. Liegen etwa beide Graphen oberhalb der x-Achse,
so gehen Sie nach folgendem (symbolisch gemeinten) Schema vor:
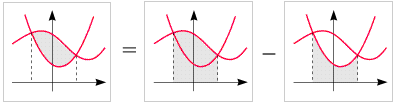
Dies lässt sich verallgemeinern auf den Fall, dass im gesamten Integrationsbereich einer der beiden
Graphen oberhalb des anderen liegt. Auch dann ist die gesuchte Fläche das bestimmte Integral
über die Differenz der beiden Funktionen.
(Beweis: Verschieben Sie alle Graphen des obigen Diagramms um dieselbe Strecke nach unten, so dass die zu berechnende
Fläche teilweise oder ganz unterhalb der x-Achse
zu liegen kommt, so fällt der Effekt dieser Verschiebung in der Differenz auf der rechten
Seite wieder heraus).
Mehr über Flächenberechnungen werden wir im Kapitel über die Anwendungen
der Integralrechnung sagen.
|
| | |

mehr über
Flächenberechnungen
(in Vorbereitung)
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Uneigentliche Integrale sind bestimmte Integrale, bei denen entweder (zumindest) eine Integrationsgrenze oder
der Integrand unendlich wird. Beide Situationen sind damit verbunden, dass die "Fläche unter dem Graphen"
ins Unendliche reicht.
Für manche Integranden strebt das bestimmte von Integral a
bis b einem wohldefinierten Wert zu,
wenn a unter jede Schranke fällt
und/oder b über jede Schranke wächst.
Für solche Fälle definieren wir
| ¥ |
|
|
b |
|
| ò |
f(x) dx
=
|
lim |
ò |
f(x) dx |
| a |
|
b ® ¥ |
a |
|
|
(28) |
| | | |

Grenzwert einer Funktion
| |
| | |
und entsprechende Grenzwerte für - ¥ als untere Grenze
sowie für das bestimmte Integral von - ¥ als untere Grenze
sowie für das bestimmte Integral von - ¥ bis ¥.
Wenn ein solcher Grenzwert nicht existiert, nennen wir das Integral divergent, ansonsten konvergent. ¥ bis ¥.
Wenn ein solcher Grenzwert nicht existiert, nennen wir das Integral divergent, ansonsten konvergent.
Beispiel:
| ¥ |
|
|
| |
¥ |
|
| ò |
|
1
x2 |
dx = - |
1
x |
|
= 1 . |
|
|
| 1 |
|
|
1 |
|
|
(29) |
Dass das Integral konvergent ist, erkennen wir daran, dass die Stammfunktion
-1/x
für x ® ¥
einen Grenzwert besitzt (nämlich 0).
Etwas oberflächlich könnte man sagen, die obere Grenze führt zu einem Beitrag
-1/¥, was
0 und daher endlich ist.
Ein anderer Typ uneigentlicher Integrale ergibt sich, wenn der Integrationsbereich (wieder im Sinn eines Grenzwerts) bis zu
einer Unendlichkeitsstelle des Integranden ausgedehnt werden kann.
Beispiel:
| 1 |
|
|
| |
1 |
|
| ò |
|
1
____
__
Ö x |
dx = 2 |
__
Ö x
|
|
= 2 . |
|
|
| 0 |
|
|
0 |
|
|
(30) |
Dass das Integral konvergent ist, erkennen wir daran, dass die Stammfunktion
2 x1/2
für x ® 0
einen Grenzwert besitzt (nämlich 0). x1/2
für x ® 0
einen Grenzwert besitzt (nämlich 0).
Das Integral desselben Integranden von einer beliebigen (positiven) unteren Grenze bis
¥ ist
übrigens ebenso divergent wie das Integral des Integranden von (29)
über das Intervall [0, 1].
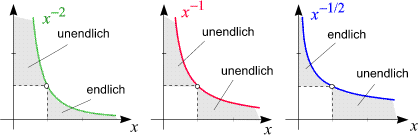
Diese Beispiele zeigen, welchen der ins Unendliche reichenden Flächenstücken unter den Graphen von
x-2 und x-1/2
ein endlicher Inhalt zugeschrieben werden kann.
Nehmen wir noch x-1 dazu (für das beide
Typen uneigentlicher Integrale divergieren), so ergibt sich folgendes Bild:
Die Endlichkeit des Inhalts einer Fläche, die bis ins Unendliche reicht, mag auf den ersten Blick wie
ein Widerspruch aussehen, ist es aber nicht: Berechnen Sie etwa den (endlichen) Flächeninhalt unter dem Graphen von
x-2
zwischen der Stelle 1 und einem großen
(aber endlichen) n, so ist das Resultat
1 - 1/n.
Wie weit auch immer Sie hinausgehen, der Flächeninhalt bleibt kleiner als
1, und im Grenzübergang
n ® ¥
strebt er gegen 1. Dieser Grenzwert ist genau das
uneigentliche Integral (29).
Verallgemeinerung: Untersuchen Sie als Übungsaufgabe das entsprechende Verhalten aller Potenzfunktionen
x-p
mit p > 0, so werden
Sie erkennen, dass
(außer für p = 1)
jede dieser Funktionen ein "endliches" und ein "unendliches" Flächenstück besitzt.
Die Situation für p > 1 ähnelt
dem im linken, jene für
p < 1
dem im rechten der drei obigen Diagramme wiedergegebenen Sachverhalte.
Ein uneigentliches Integral, dessen Wert schwieriger zu erhalten ist als die bisher betrachteten, ist dieses:
| ¥ |
|
|
|
| ò |
e-x2 dx
=
|
__
Ö p
|
. |
| -¥ |
|
|
|
|
(31) |
Seinen Beweis heben wir uns für ein späteres Kapitel auf.
Es wird in der Wahrscheinlichkeitsrechnung und Statistik benötigt. Der Integrand
exp(-x2)
stellt die so genannte Normalverteilung dar, sein Graph
heißt Gaußsche Glockenkurve. Sehen Sie sich deren Verlauf im
Funktions-Plotter an!
Ganz allgemein wird eine im Unendlichen verschwindende Funktion der Form
exp(Q),
wobei Q ein quadratischer Ausdruck (in einer oder mehreren Variablen) ist,
als Gauß-Funktion bezeichnet. Ein Integral über eine solche Funktion
- wie (31) - heißt Gaußsches Integral.
| | | |

Beweis
(in Vorbereitung)

Normalverteilung
(in Vorbereitung)
| |
| | |
Weitere Beispiele für uneigentliche Integrale finden Sie unter den bestimmten Integralen
unserer Zusammenstellung
Wir verzichten auf ihre detaillierte Herleitung. (Übungsaufgabe: Finden Sie aus der Liste die
uneigentlichen Integrale heraus!)
Bemerkung: Für uneigentliche Integrale gelten der Hauptsatz (12) und
die Integrationsregeln, die wir oben
besprochen haben, in entsprechend adaptierter Weise. Dabei sollte insbesondere beachtet werden,
dass ein Ausdruck wie F(¥)
als Grenzwert zu verstehen ist.
Mit dem nebenstehenden Button können Sie ein Beispiel für die Anwendung der Substitutionsmethode
(obige Regel 7) auf solche Integrale aufrufen.
Es handelt sich um ein Gaußsches Integral wie (31), nur dass der Exponent
-x2 durch den allgemeineren Ausdruck
-ax2 + bx
ersetzt wird. Als zusätzliche Technik wird dabei das "Ergänzen auf ein vollständiges
Quadrat", das wir in einem früheren Kapitel bei der Lösung quadratischer Gleichungen benutzt haben, verwendet.
|
| | |

Ergänzen auf ein vollständiges Quadrat
| |
| | |
| Das Integral als Grenzwert von Summen |
| | | |
Zum Seitenanfang | |
| | |
Das "Flächeninhaltsproblem" für
stetige Funktionen haben wir mit Hilfe des Hauptsatzes der Differential- und Integralrechnung
gelöst: Man suche eine Stammfunktion (die immer existiert) und berechne
den (orientierten) Flächeninhalt mittels (12).
Was aber ist die allgemeinste Klasse von Funktionen, für die die Idee des (orientierten)
"Flächeninhalts unter dem Graphen" einen Sinn macht, und wie ist dieser
definiert?
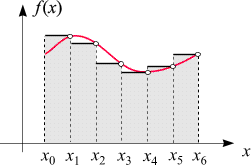 Darauf hat Bernhard Riemann im 19. Jahrhundert die erste befriedigende Antwort gegeben. Seine Konstruktion
beruht darauf, eine gegebene Funktion von unten und oben durch so genannte Treppenfunktionen
einzuzwicken. Mit Hilfe deren Integrale, der Untersummen und Obersummen,
wird definiert, wann eine Funktion integrierbar im Sinne von Riemann
(auch Riemann-integrierbar) ist. Für stetige Funktionen lässt sich
das bestimmte Integral - so, wie man es intuitiv auch erwartet
- sehr leicht als Grenzwert einer Folge von Rechtecksflächen
(den so genannten Riemann-Summen, siehe nebenstehende Skizze) darstellen.
Daraus ergeben sich Möglichkeit zur numerischen Approximation bestimmter Integrale.
Riemann-Summen können auch dazu benutzt werden, um intuitive Argumentationen mit "infinitesimalen"
Größen durch exakte zu ersetzen.
Für Näheres darüber siehe den nebenstehenden Button.
Zur Berechnung von Riemann-Summen steht ein Online-Werkzeug zur Verfügung,
siehe unten.
Darauf hat Bernhard Riemann im 19. Jahrhundert die erste befriedigende Antwort gegeben. Seine Konstruktion
beruht darauf, eine gegebene Funktion von unten und oben durch so genannte Treppenfunktionen
einzuzwicken. Mit Hilfe deren Integrale, der Untersummen und Obersummen,
wird definiert, wann eine Funktion integrierbar im Sinne von Riemann
(auch Riemann-integrierbar) ist. Für stetige Funktionen lässt sich
das bestimmte Integral - so, wie man es intuitiv auch erwartet
- sehr leicht als Grenzwert einer Folge von Rechtecksflächen
(den so genannten Riemann-Summen, siehe nebenstehende Skizze) darstellen.
Daraus ergeben sich Möglichkeit zur numerischen Approximation bestimmter Integrale.
Riemann-Summen können auch dazu benutzt werden, um intuitive Argumentationen mit "infinitesimalen"
Größen durch exakte zu ersetzen.
Für Näheres darüber siehe den nebenstehenden Button.
Zur Berechnung von Riemann-Summen steht ein Online-Werkzeug zur Verfügung,
siehe unten.
| | | |

Treppenfunktionen

numerische Integration
(in Vorbereitung)
Das
Integral
| |
| | |
Eine Weiterentwicklung des Integralbegriffs, auf deren Details wir hier aber nicht näher eingehen,
stammt von Henri Léon Lebesgue (ausgesprochen [lebäk]). Das Lebesgue-Integral ist die
wichtigste Grundlage der heutigen Integrationstheorie, die unter dem Namen Maßtheorie bekannt ist
und weniger auf die Idee der "Fläche unter dem Graphen" zielt als vielmehr
auf das Integral (Maß) als kontinuierlicher Verallgemeinerung des Mittelwerts
- ein Thema, das wir bereits oben angesprochen haben
und im Kapitel über die Anwendungen der Integralrechnung wieder aufnehmen werden.
Diese modernen Konzepte werden beispielsweise im Formalismus der Quantentheorie
benötigt.
|
| | |

Anwendungen der
Integralrechnung
(in Vorbereitung)
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Da es - im Gegensatz zum Differenzieren -
kein Schema gibt, die Stammfunktion einer termdefinierten Funktion auf jene ihrer Bestandteile
zu reduzieren, sind auch elektronische Hilfen darauf angewiesen, verschiedene Möglichkeiten durchzuprobieren.
Sofern es sich nicht um sehr ausgefallene Funktionen handelt, sind sie darin viel schneller als
Menschen, und viel Erfahrung ist in ihre Programmierung eingeflossen.
Die meisten Computeralgebra-Systeme
(wie Mathematica,
Maple,
DERIVE,
TI-92 und
TI-89/Voyage 200)
können integrieren. Bedenken Sie bei der Verwendung solcher Programme aber bitte:
- Es besteht keine Garantie auf ein Resultat.
- Manchmal werden Funktionen ausgegeben, deren Namen Sie vielleicht nicht kennen. (Integrieren Sie beispielsweise
e-x2,
so kann das Resultat die Bezeichnung "erf" oder "Erf" - für error function - enthalten).
In der Regel bedeutet das, dass die angegebene Funktion nicht geschlossen integrierbar (s.o.),
für gewisse Zwecke aber wichtig genug ist, um einen eigenen Namen erhalten zu haben.
- Obwohl die von Computeralgebra-Systemen verwendeten Algorithmen immer besser und Fehler immer seltener werden,
sollten Sie, wenn sie ganz sicher gehen wollen, einen als Stammfunktion ausgegebenen Funktionsausdruck
durch Differenzieren überprüfen.
- Bei der Berechnung von bestimmten Integralen ist besondere Vorsicht geboten: Ist die Stammfunktion
F
einmal gefunden, so ist das bestimmte Integral von a bis
b durch die Differenz
F(b) - F(a)
gegeben. Natürlich können Computer diese Einsetzung vornehmen. Es ist für sie aber
nicht in jedem Fall leicht, zu erkennen, ob zwischen den Stellen a und
b Singularitäten liegen, d.h. ob der als
Stammfunktion vorgeschlagene Term tatsächlich eine im gesamten Integrationsbereich differenzierbare
Funktion ist, deren Ableitung mit dem Integranden übereinstimmt! Obwohl Computeralgebra-Systeme derartige Fehlerquellen immer
besser erkennen, sollten Sie, wenn Sie ganz sicher gehen wollen, eine eigene Überprüfung durchführen.
- Manchmal bietet das Ergebnis einer numerischen (d.h. näherungsweisen) Integration eine zusätzliche
Überprüfung.
Im Rahmen des an der Vanderbilt University zur Verfügung gestellten
MathServ Project
finden Sie die auf Mathematica beruhenden Online-Werkzeuge
(hier antidifferentiation bzw. antiderivative genannt) wobei Sie Funktionsterm und Variablennamen eingeben können, und
(definite integral) wobei Sie Funktionterm, Variablenname und die (endlichen) Integrationsgrenzen eingeben können.
Falls das Programm den exakten Wert den Integrals findet, wird dieser ausgegeben, in jedem Fall aber auch
eine numerische Approximation.
Darüber hinaus bietet MathServ weitere Online-Programme, die beim Verstehen des Integrierens und seiner Methoden helfen, an:
- Im Integration Assistant
können Sie die Anwendung verschiedener Integrationsregeln (s.o.)
durchspielen: Geben Sie einen Funktionsterm ein und wählen Sie die gewünschte Methode.
Das Programm versucht dann, sie durchzuführen.
- Ein spezielles Werkzeug berechnet die Partialbruchzerlegung
(siehe oben) einer eingegebenen rationalen Funktion (integriert aber nicht).
- Weiters können Sie bestimmte Integrale als Riemann-Summen
(siehe oben) mit einer von Ihnen vorgegebenen Genauigkeit approximieren.
Ein berühmtes Programm ist The Integrator
von Wolfram Research.
Hier muß die Wirkung von Funktionen allerdings gemäß der
Mathematica-Syntax mit eckigen Klammern
und Großschreibung bezeichnet werden! Beispiel:
Tan[x] + x^2 Exp[-x], nicht tan(x) + x^2 exp(-x).
Falls es zu Ihren Lernzielen gehört, die Integralrechnung eingehend zu beherrschen, versuchen Sie trotz dieser Hilfen,
das "händische" Integrieren ein bisschen zu üben, damit Sie
wissen, was diese Programme machen.
Näherungsweise numerische Integrationstechniken, bei denen Computer einen entscheidende Rolle
spielen, besprechen wir in einem eigenen Kapitel.
|
| | |

numerische Integration
(in Vorbereitung)
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Die Integralrechnung erlaubt eine Fülle von Anwendungen, insbesondere in der Mathematik,
in den Naturwissenschaften und in der Technik.
Hier einige der Anwendungen, denen Sie in anderen Kapiteln begegnen werden:
- Ein eigenes Kapitel ist der Erschließung einiger Anwendungen der Integralrechnung
gewidmet. In ihm werden wir Flächen behandeln, die von beliebigen Kurven begrenzt werden
(z.B. anhand der Kreisfläche eine genaue Definition der Zahl p
geben) und uns mit Volumsberechnungen, der Ermittlung der Länge einer Kurve
und Schwerpunktberechnungen beschäftigen.
Insbesondere letzteres gibt dem bestimmten Integral eine weitere Deutung, die wir bereits
oben erwähnt haben:
als kontinuierliche Verallgemeinerung des Mittelwerts von Zahlen bzw. des Begriffs der Summe.
- In der Wahrscheinlichkeitsrechnung treten so genannte kontinuierliche
Verteilungen auf (ein Beispiel ist der Integrand von (31)), die mit Hilfe des Integralbegriffs interpretiert werden.
- Ein anderes Kapitel ist der Integration von Funktionen in mehreren Variablen und
den so genannten Integralsätzen vorbehalten. Mit ihrer Hilfe können
beispielsweise elektromagnetische Felder oder Strömungsverhältnisse in Flüssigkeiten
analysiert werden.
- Integration ist unabdingbar bei der Lösung von Differentialgleichungen.
So werden etwa physikalische Bewegungsgesetze in Form von Differentialgleichungen
aufgeschrieben - um aber konkrete Bewegungsabläufe zu erhalten,
müssen wir diese Gleichungen lösen.
- Integralrechnung spielt in der Theorie der Fourierreihen
eine wichtige Rolle.
- Im Rahmen der komplexen Zahlen ergibt sich ein Integrationsbegriff, die so genannte
komplexe Integration, der sich vom hier
besprochenen erheblich unterscheidet. Im Kapitel über die komplexen Zahlen haben wir
dazu ein paar Bemerkungen gemacht.
Damit sind wir am Ende dieses Kapitels angelangt.
Kehren Sie bei Bedarf später wieder zu ihm zurück, um die der Integralrechnung zugrunde liegenden Ideen
und die Regeln fürs praktische Rechnen zu wiederholen.
|
| | |

Anwendungen der
Integralrechnung
(in Vorbereitung)

kontinuierliche Verteilungen
(in Vorbereitung)

Integralsätze
(in Vorbereitung)

Differentialgleichungen
(in Vorbereitung)

Fourierreihen

komplexe Zahlen
| |