Größere Schriftzeichen   

Besondere Punkte und Linien im Dreieck:

Wir führen die Beweise (bzw. geben in einem Fall nur die Beweisidee) einiger Eigenschaften betreffend die vier "merkwürdigen Punkte" im 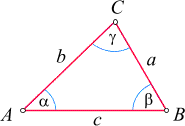Dreieck:
Satz 1: Die drei Seitensymmetralen eines Dreiecks schneiden einander im Umkreismittelpunkt.

Beweis: Betrachten wir zunächst die Seitensymmetrale von AB. Sie besteht aus allen Punkten, die von A und B den gleichen Abstand haben. Jeder Punkt auf dieser Seitensymmetrale ist der Mittelpunkt eines Kreises, auf dem A und B liegen. (Und umgekehrt ist die Seitensymmetrale die Menge aller dieser Kreismittelpunkte). Ein solcher Kreis − mit Mittelpunkt M − ist hier dargestellt:


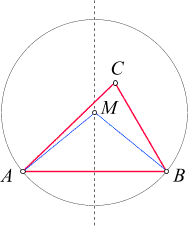
Nun lassen wir M so lange nach unten wandern, bis auch der Punkt C auf dem Kreis liegt. Der so erhaltene Kreis ist der Umkreis des Dreiecks, seinen Mittelpunkt nennen wir U:


Ist der Mittelpunkt weiter oben oder unten, so liegt C nicht auf dem betreffenden Kreis. Das erweist die Existenz eines (eindeutigen) Umkreises.

U ist nun aber von allen drei Eckpunkten gleich weit entfernt, liegt also auch auf der Seitensymmetrale von BC sowie auf jener von CA. Damit ist bewiesen, dass U der Schnittpunkt der drei Steckensymmetralen ist.


Satz 2: Die drei Höhenlinien eines Dreiecks schneiden einander in einem Punkt (dem Höhenschnittpunkt).

Beweis: Ein besonders eleganter Beweis (der auf Leonhard Euler zurückgeht) ergibt sich, wenn wir unserem Dreieck ABC durch Parallelverschieben der Seiten noch vier (um 180° gedrehte) Dreiecke hinzugesellen:


Betrachten Sie nun die drei strichlierten Geraden:


Es sind die Seitensymmetralen des großen Dreiecks A'B'C'. Gemäß Satz 1 (s.o.) schneiden Sie einander in einem Punkt. Gleichzeitig sind es aber die Höhen unseres ursprünglichen Dreiecks ABC, womit bewiesen ist, dass sich die drei Höhen eines Dreiecks in einem Punkt schneiden!


Satz 3: Die drei Winkelsymmetralen eines Dreiecks schneiden einander im Inkreismittelpunkt.

Beweis: Betrachten wir zunächst die Winkelsymmetrale von α. Sie besteht aus allen Punkten, die von den Seitenlinien b und c den gleichen Normalabstand haben. Jeder Punkt auf dieser Winkelsymmetrale ist der Mittelpunkt eines Kreises, der diese beiden Seitenlinien berührt. (Und umgekehrt ist die Winkelsymmetrale die Menge aller dieser Kreismittelpunkte). Ein solcher Kreis ist hier dargestellt:


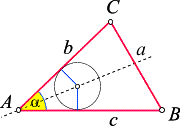
Nun lassen wir seinen Mittelpunkt so lange entlang der Winkelsymmetralen auf die Seite a zu wandern, bis der Kreis auch diese berührt. Der so erhaltene Kreis ist der Inkreis des Dreiecks, seinen Mittelpunkt nennen wir I:


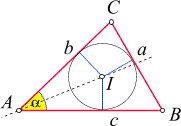
Ist der Mittelpunkt nicht weit genug oder zu weit gerutscht, so berührt der Kreis die Seite a nicht. Das erweist die Existenz eines (eindeutigen) Inkreises (d.h. eines Kreises, der alle drei Seitenlinien von innen berührt).

I ist nun aber Winkelsymmetrale aller drei Winkel, d.h. auch von β und γ. Damit ist bewiesen, dass I der Schnittpunkt der drei Winkelsymmetralen ist.


Satz 4: Die drei Schwerlinien eines Dreiecks schneiden einander in einem Punkt (dem Schwerpunkt).

Beweis: Wir betrachten die Schwerlinie auf die Seite c, d.h. die Gerade durch C und den Halbierungspunkt D der Seite c:


Sie teil das Dreieck in zwei flächengleiche Teildreiecke ACD und DBC. Die beiden Teildreiecke sind deshalb flächengleich, weil sie die gleiche Höhe w haben:


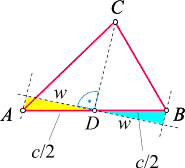
Dieser Sachverhalt gilt klarerweise auch für die anderen Schwerlinien, und wir merken uns: Eine Schwerlinie eines Dreiecks teilt dieses in zwei flächengleiche Teildreiecke.

Wir betrachten nun eine zweite Schwerlinie und bezeichnen den Schnittpunkt der beiden Schwerlinien mit S:


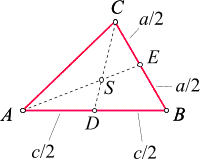
Die beiden Schwerlinien teilen das Dreieck in vier Teildreiecke


mit Flächeninhalten A1 bis A4, für die A1 + A3 = A2 + A4 und A1 + A2 = A3 + A4 gilt. Die Differenz dieser beiden Gleichungen führt sofort auf A2 = A3 und A1 = A4. Die beiden gelben Bereiche sind daher gleich flächengleich und ebenso die beiden türkisfarbenen.

Wir zeichnen nun den Halbierungspunkt F der Seite b und ziehen die Strecken SF und SB:


Beachten Sie: Die Strecken beiden SF (blau) und SB (grün) sind unabhängig voneinander zustande gekommen. Sind sie zueinander parallel, d.h. liegen sie auf einer Geraden? Um diesen Punkt zu klären, beobachten wir: Aus A2 = A3 folgt daher, dass alle sechs Teildreiecke in der obigen Skizze flächengleich sind! Folglich teilt die Linie, die von B über S zu F führt, das gegebene Dreieck in zwei flächengleiche Stücke. Andererseits tut das die Strecke BF (die ja eine Schwerlinie ist) auch. Die Linie von B über S zu F kann daher keinen Knick haben! Es handelt sich genau um die dritte Schwerlinie, die Strecke BF. Damit ist bewiesen, dass sich die drei Schwerlinien eines Dreiecks in einem Punkt S (dem Schwerpunkt) schneiden.

Nachbemerkungen:

Satz 5: In jedem Dreieck liegen Höhenschnittpunkt, Umkreismittelpunkt und Schwerpunkt auf einer Geraden (der Eulerschen Geraden).

Beweisidee: Der Beweis beruht auf einem Vergleich der Dreiecke ABC und DEF, wobei letzteres aus den Halbierungspunkten der Seiten entsteht (siehe die letzte Skizze oben). Die Argumentation ist verwandt mit der, die wir für Satz 2 (s.o.) benutzt haben. Wenn er Sie im Detail interessiert, finden Sie ihn (zusammen mit einem Java-Applet, in dem Sie die Dreieckspunkte durch Mausziehen dynamisch verändern können) im Programm von mathematik.ch auf der Seite Eulersche Gerade mit Geometry Applet.