Bemerkungen zur Variablensubstitution:
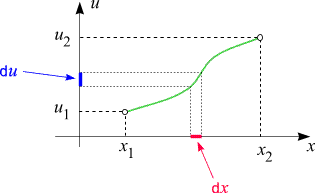
Das Diagramm illustriert eine umkehrbare Entsprechung zwischen
den Variablen x und u.
Als Funktion
u º u(x)
aufgefasst, bildet sie das Intervall
[x1, x2]
bijektiv auf das Intervall
[u1, u2]
ab. Die dazu inverse Funktion
x º x(u)
bildet das Intervall
[u1, u2]
bijektiv auf das Intervall
[x1, x2]
ab.
Wir können die Ableitung
u'(x)
an irgendeiner Stelle x als du/dx
bzw. die Ableitung
x'(u)
der inversen Funktion
an der entsprechenden u-Stelle als dx/du
schreiben.
Wie wir von der Diskussion der Ableitung der inversen Funktion
im Kapitel Differenzieren 1
wissen, sind diese beiden Ableitungen Kehrwerte voneinander:
u'(x) = 1/x'(u),
was sehr schön mit der Schreibweise als "Differentialquotienten" übereinstimmt:
du/dx
= 1/(dx/du).
Gestatten wir uns die Vorstellung, dass es sich bei den
"Differentialen" dx und
du um
"kleine Änderungen" von
x und
u handelt,
so können wir diese ineinander umrechnen:
du = u'(x) dx
dx = x'(u) du.
Der obigen der Skizze können Sie die geometrische Bedeutung
dieser Formeln entnehmen.
In der Hauptsache ist es diese Übersetzung, die wir bei der Variablensubstitution
in Integralen durchführen.

