Sei a > 0,
und sei
e ® F(e)
eine Funktion, die für
-a < e
und
e < a,
nicht aber
an der Stelle e = 0
definiert ist.
Was ist der Grenzwert lim e ® 0 F(e) ?
Intuitiv existiert dieser Grenzwert, wenn
F(e)
gegen eine Zahl K strebt, wann immer
e schrittweise gegen 0
strebt.
Die Formulierung wann immer bezieht sich darauf, dass die Art und Weise, wie sich
e schrittweise an 0
annähert, beliebig sein soll.
Das bedeutet, dass wir
- eine beliebige Folge von Zahlen
e1,
e2,
e3,
e4,
e5,...
aus dem Definitionsbereich von F
wählen können, für die
lim n ® ¥ en = 0 gilt,
- und für jede dieser Folgen
lim n ® ¥ F(en) = K
erhalten. Mit anderen Worten: Die zugehörige Folge der Funktionswerte
F(e1),
F(e2),
F(e3),
F(e4),
F(e5),...
strebt immer
gegen dieselbe Zahl K.
Ist das der Fall, so schreiben wir
lim e ® 0 F(e)
= K
und bezeichnen K als den Grenzwert der
Funktion F für
e ® 0.
Auf diese Weise kann also der Grenzwert einer Funktion aus dem Begriff des
Grenzwerts einer Zahlenfolge (der der intuitiven Idee einer "schrittweisen" Annäherung
entspricht) erhalten werden.
Falls
lim n ® ¥ F(en)
von der gewählten Folge
e1,
e2,
e3,
e4,
e5,...
abhängt oder (für auch nur eine solche Folge)
nicht existiert, so sagen wir, dass der Grenzwert
lim e ® 0 F(e)
nicht existiert.
|
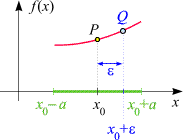 zumindest in einem Intervall
x0 - a < x < x0 + a,
d.h. in einer Nachbarschaft (Umgebung) von x0, definiert ist.
Damit ist sichergestellt, dass für genügend kleine e
(genauer: wenn -a < e < a ist)
der Funktionswert f(x0 + e)
existiert. Wie im nebenstehenden Diagramm illustriert, ist dann auch der Punkt
Q mit Koordinaten
zumindest in einem Intervall
x0 - a < x < x0 + a,
d.h. in einer Nachbarschaft (Umgebung) von x0, definiert ist.
Damit ist sichergestellt, dass für genügend kleine e
(genauer: wenn -a < e < a ist)
der Funktionswert f(x0 + e)
existiert. Wie im nebenstehenden Diagramm illustriert, ist dann auch der Punkt
Q mit Koordinaten
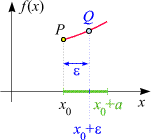 ein Randpunkt dieses Intervalls, so muss man die obige Definition leicht abwandeln, um etwas über Existenz
(oder Nicht-Existenz) einer Tangente mit wohldefiniertem Anstieg im Punkt
(x0, f(x0))
aussagen zu können:
Ist beispielsweise f
nur für x ³ x0
(oder für
x0 £ x < x0 + a)
definiert, so kann die "rechtsseitige Ableitung" von f
an der Stelle x0 dadurch definiert werden,
dass die Folgenglieder, die für e in den
Differenzenquotienten (1) eingesetzt werden, positiv gewählt werden müssen
(d.h. "von oben kommend" gegen 0 streben).
In diesem Fall liegt Q immer
rechts von P.
Auf diese Weise stellt sich etwa heraus,
ein Randpunkt dieses Intervalls, so muss man die obige Definition leicht abwandeln, um etwas über Existenz
(oder Nicht-Existenz) einer Tangente mit wohldefiniertem Anstieg im Punkt
(x0, f(x0))
aussagen zu können:
Ist beispielsweise f
nur für x ³ x0
(oder für
x0 £ x < x0 + a)
definiert, so kann die "rechtsseitige Ableitung" von f
an der Stelle x0 dadurch definiert werden,
dass die Folgenglieder, die für e in den
Differenzenquotienten (1) eingesetzt werden, positiv gewählt werden müssen
(d.h. "von oben kommend" gegen 0 streben).
In diesem Fall liegt Q immer
rechts von P.
Auf diese Weise stellt sich etwa heraus,