Beispiel für eine nichtdifferenzierbare Funktion

Größere Schriftzeichen

Beispiel für eine nichtdifferenzierbare Funktion:

Nicht jeder Funktionsgraph besitzt in jedem Punkt eine Tangente. Beispielsweise hat der Graph der Betragsfunktion
f(x) = |x|
im Ursprung einen Knick. Was passiert, wenn wir versuchen, die Ableitung dieser Funktion an der Stelle x₀ = 0 zu berechnen? Gemäß Formel (2) wäre sie durch

		\|ε\| ε
f '(0) =	lim
	ε → 0

gegeben. An dieser Stelle ist es entscheidend, was unter dem Grenzprozess ε → 0 genau gemeint ist: Wenn für ε nacheinander irgendwelche Zahlen, die gegen 0 streben (und selbst ≠0 sind) eingesetzt werden, so muss die daraus entstehende Folge der Differenzenquotienten immer gegen dieselbe Zahl K streben, unabhängig davon, welche Zahlen für ε man nun konkret gewählt hat − die Zahl K würden wir dann als f '(0) bezeichnen. Probieren wir ein paar Möglichkeiten aus:

Setzen wir für ε nacheinander 1, 1/2, 1/3,..., so ist die zugehörige Folge der Differenzenquotienten 1, 1, 1,..., d.h. ihr Grenzwert ist 1.
Setzen wir für ε nacheinander −1, −1/2, −1/3,..., so ist die zugehörige Folge der Differenzenquotienten −1, −1, −1,..., d.h. ihr Grenzwert ist −1.
Setzen wir für ε nacheinander 1, −1/2, 1/3, −1/4..., so ist die zugehörige Folge der Differenzenquotienten 1, −1, 1, −1..., besitzt also überhaupt keinen Grenzwert.

Daher ist die Betragsfunktion an der Stelle 0 nicht differenzierbar. Anders ausgedrückt: Der Grenzwert

			\|ε\| ε
	lim
	ε → 0

existiert nicht.

Dieses Verhalten der Differenzenquotienten ist

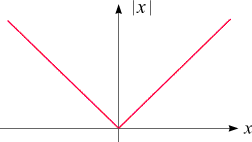unmittelbar aus der Form des Graphen der Betragsfunktion zu verstehen: Er besteht aus zwei Halbgeraden ("Ästen"), die einander im Ursprung treffen und dort einen Knick bewirken. Der Differenzenquotient |ε|/ε ist der Anstieg der Sekante durch die Punkte (0, 0) und (ε, |ε|). Letzterer befindet sich für ε > 0 am rechten, für ε < 0 am linken Ast des Graphen. Im ersten Fall ist der Anstieg der Sekante 1, im zweiten ist er −1.

Ob sich der Differenzenquotient |ε|/ε für ε → 0 einer Zahl annähert (und wenn, welcher), hängt davon ab, wie ε gegen 0 strebt. Daran erkennen wir rein rechnerisch, was geometrisch betrachtet klar ist: dass der Graph der Betragsfunktion im Punkt (0, 0) keine (eindeutige) Tangente besitzt. (Wer will, kann von einer "rechtsseitigen" Tangente mit Anstieg 1 und einer "linksseitigen" Tangente mit Anstieg −1 sprechen. Aber auch dann bleibt die Tatsache bestehen, dass es keine eindeutige Tangente gibt).

Damit eine Funktion an einer gegebenen Stelle als differenzierbar gilt, darf das Verhalten des Differenzenquotienten im Grenzübergang nicht davon abhängen, wie ε gegen 0 strebt. Nur dann können wir von der Existenz einer (eindeutigen) Tangente an den Graphen sprechen.