|
2.1 Einleitung
|

 
|
Im vorherigen Kapitel wurden die Winkelfunktionen im rechtwinkeligen Dreieck definiert, also folglich nur für Winkel zwischen 0- und 90 Grad bzw. 0- und π/2 rad.
Die Frage ist nun: Gibt es z.B. einen Cosinus von 186°? - Und falls ja...
|
|
2.2 ...was ist der Cosinus von 186°?
|

 


|
Um diese Frage zu beantworten muss man zunächst etwas ausholen und die Winkelfunktionen am Einheitskreis definieren.
Zuvor aber noch eine Information zu diesem Kapitel: Die Kennzeichnung "Lerntagebuch" bedeutet in diesem Fall, dass du dir die wichtigsten Inhalte niederschreiben-, bzw. dass du die wichtigsten Aufträge ausführen solltest. Um dir die Entscheidung, welche das sind, zu erleichtern, wurden sie mit dem folgenden Symbol gekennzeichnet: "►"
Konstruktion der Winkelfunktionen im 1. Quadranten des Einheitskreises
Wie der Name vl. schon vermuten lässt, ist der Einheitskreis ein Kreis, dessen Radius genau "eine Einheit" (cm, dm, m,...) lang ist, und diese Eigenschaft macht es möglich die Werte der trigonometrischen Funktionen von beliebigen Winkeln grafisch darzustellen.
► Zeichne zunächst ein Koordinatensystem und konstruiere darin einen Kreis mit dem Radius r = 1dm und dem Mittelpunkt M=(0|0).
Der Kreis erstreckt sich über alle 4 Abschnitte des Koordinatensystems, genannt "Quadranten", wie unten zu sehen ist:
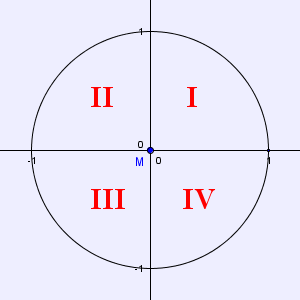
Sinus und Cosinus
► Schreibe nun dem ersten Quadranten ein rechtwinkeliges Dreieck, wie unten abgebildet, ein.
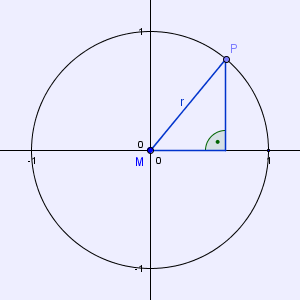
Da der Kreis den Radius r = 1 hat, ist die Hypotenuse des blauen rechtwinkeligen Dreiecks ebenfalls nur eine Einheit lang und es folgt:
Gegenkathete Gegenkathete
sin(φ) = -------------- = -------------- = Gegenkathete
Hypotenuse 1
Ankathete Ankathete
cos(φ) = ----------- = ----------- = Ankathete
Hypotenuse 1
► Markiere nun den sin(φ) und den cos(φ) als Gegenkathete und Ankathete des Dreiecks und schon kannst du mithilfe deiner Skizze die entsprechenden Werte direkt bestimmen, indem du ihre Länge in dm abmisst.
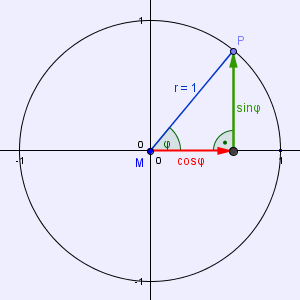
Tangens
Nun ist ein Dreieck gesucht dessen Ankathete gleich 1 ist, damit, ähnlich wie bei Sinus und Cosinus, wieder gilt:
Gegenkathete Gegenkathete
tan(φ) = -------------- = ------------- = Gegenkathete
Ankathete 1
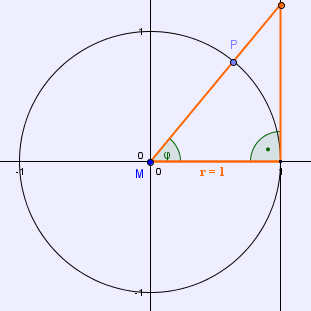
Der tan(φ) entspricht demnach der Gegenkathete dieses Dreiecks und du kannst seinen Wert wieder bestimmen, indem du die Länge der Gegenkathete in dm abmisst.
► Füge nun auch den tan(φ) deiner Skizze zu, um die Winkelfunktionen im 1. Quadranten des Einheitskreises zu vervollständigen:
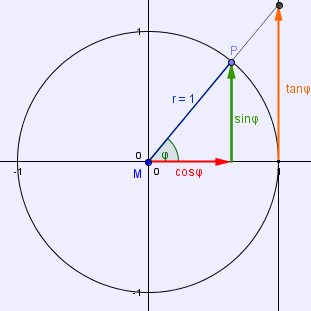

Konstruktion der Winkelfunktionen im 2. Quadranten des Einheitskreises
Auch hier wird dem Quadranten wieder ein rechtwinkeliges Dreieck eingeschrieben, von dem eine Kathete auf der x-Achse liegt.
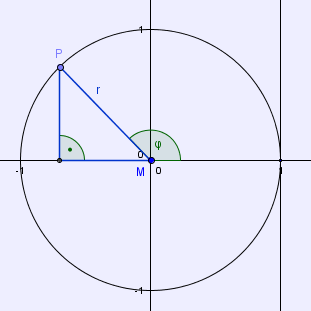
►Die drei Merksätze, die für den ersten Quadranten hergeleitet wurden, gelten genau so auch für diesen- und die weiteren Quadranten, und du kannst sin(φ), cos(φ) und tan(φ) für 90° < φ < 180° wie folgt darstellen:
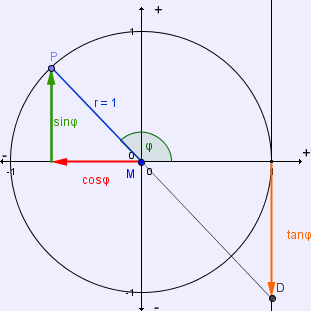
Hier ist es nun wichtig auf die Richtung der Pfeile zu achten. Zwar kannst du die jeweiligen Werte für sinus, cosinus und tangens wieder direkt ablesen, allerdings sind in diesem Fall (d.h. im zweiten Quadranten) Cosinus und Tangens negativ.

Konstruktion der Winkelfunktionen im 3.- und 4. Quadranten des Einheitskreises
► Im folgenden Bild kannst du erkennen, wie sin(φ), cos(φ) und tan(φ) im 3. Quadranten, also für 180° < φ < 270° definiert sind. Überlege dir selbst, wie das Ganze im 4. Quadranten aussieht und übertrage dann beide Skizzen in dein Lerntagebuch! (Keine Angst - du wirst später die Möglichkeit haben deine Lösung für den 4. Quadranten zu überprüfen)
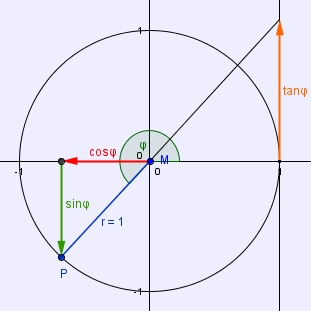
"Kritische" Stellen
Aufmerksamen Lesern sollte aufgefallen sein, dass bisher die Randpunkte der Quadranten ausgenommen wurden.
Das liegt daran, dass die rechtwinkeligen Dreiecke an diesen Stellen bloß Strecken der Länge 1 sind, wodurch die Skizzen für die jeweiligen Quadranten für diese Werte nicht herangezogen werden können.
►Sinus und Cosinus stellen als Koordinaten des Punktes P keine große Schwierigkeit dar, den Tangens an diesen "kritischen" Stellen muss man sich allerdings kurz überlegen:
1) φ = 0° bzw. 0 rad
P = (0|1). Die Gerade, die durch P und M geht, verläuft somit entlang der x-Achse und "schneidet" die Tangente im Berührpunkt selbst.
sin(0) = 0 cos(0) = 1 tan(0) = 0
2) φ = 90° bzw. π/2 rad
P = (0|1). Die Gerade, die durch P und M geht, verläuft somit entlang der y-Achse und schneidet die Tangente nie.
Der Tangens ist an dieser Stelle also nicht definiert.
sin(π/2) = 1 cos(π/2) = 0 tan(π/2) existiert nicht
3) φ = 180° bzw. π rad
P = (-1|0). Die Gerade, die durch P und M geht, verläuft somit entlang der x-Achse - siehe 1)
sin(π) = 0 cos(π) = -1 tan(π) = 0
4) φ = 270° bzw. 3·π/2 rad
P = (0|-1). Die Gerade, die durch P und M geht, verläuft somit entlang der y-Achse und schneidet die Tangente nie.
sin(3·π/2) = -1 cos(3·π/2) = 0 tan(3·π/2) existiert nicht
Eintrag in das Lerntagebuch
|
|
2.4 Die Periodizität der Winkelfunktionen
|

 

|
In den vorigen Abschnitten haben wir die trigonometrischen Funktionen von Winkeln zwischen 0° und 360° definiert.
Tatsächlich existiert aber auch beispielsweise ein sin(-45°) oder ein cos(12345°) und man kann die trigonometrischen Funktionen für beliebige Winkel definieren, was wir im folgenden Abschnitt versuchen wollen.
Beliebige Winkel in Einheitskreis
Starte zunächst wieder das oben verlinkte Applet und bewege den Punkt P entgegen dem Uhrzeigersinn entlang der Kreislinie.
Der Winkel wird stetig zunehmen um dann - genau wenn der volle Winkel (360° bzw. 2·π rad) erreicht wurde - plötzlich wieder bei 0 zu beginnen.
Tatsächlich nimmt er aber auch hier noch weiter zu und hat eigentlich den Wert: 360° + α.
Dasselbe gilt auch wenn man den Punkt P im Uhrzeigersinn entlang der Kreislinie bewegt: Der Winkel wird stetig abnehmen um dann - genau bei 0° - plötzlich wieder bei 360 zu beginnen.
Tatsächlich nimmt er aber auch hier weiter ab und hat somit den Wert: α - 360° = -α
Periodizität von Sinus und Cosinus
Der Punkt P kann also eine Umdrehung nach der anderen beschreiben und obwohl der Winkel immer größer/kleiner wird, wiederholen sich die Funktionswerte der trigonometrischen Funktionen nach jeder vollen Umdrehung in eine Richtung.
...sin(α-360°) = sin(α) = sin(α+360°)... = sin(α+k·360°)
...cos(α-2π) = cos(α) = cos(α+2π)... = cos(α+k·π) , k Є 
Aus diesem Grund werden Sinus und Cosinus "2·π-periodisch" genannt.
Periodizität des Tangens
Der Tangens ist ebenfalls periodisch, hat aber ein noch kleineres Periodizitätsintervall, da sich seine Werte schon nach jeder halben Umdrehung wiederholen.
...tan(α-180°) = tan(α) = tan(α+180°)... = tan(α+k·18°), k Є 
Man nennt ihn daher "π-periodisch"
Die Funktionsgraphen der Winkelfunktionen
Besonders schön lässt sich diese Periodizitätseigenschaft der Winkelfunktionen mithilfe ihrer Funktionsgraphen sichtbar machen.
Starte nun die leicht veränderte Version des obigen Applets, indem du dem folgenden Link folgst und lasse dann die jeweiligen Funktionsgraphen "erscheinen".
Applet zu Winkelfunktionen am Einheitskreis - mit Spur
Eintrag in das Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



