|
2.1 Wichtige Eigenschaften
|

 

|
- Gebrochen rationale Funktionen sind Funktionen, deren Funktionsterm ein Bruchterm ist.
(Zur Erklärung: Bruchterme sind Brüche bei denen eine Variable im Nenner auftritt)
- Alle Zahlen, für die der Nenner null wird, können nicht zur Definitionsmenge der Funktion gehören. Diese Stellen nennt man auch „Definitionslücken“.
- Eine Gerade, der sich der Graph einer Funktion beliebig annähert, nennt man „Asymptote“.
Man unterscheidet zwischen waagrechten und senkrechten Asymptoten.
- Eine Stelle, bei der der Graph eine senkrechte Asymptote aufweist, nennt man auch „Polstelle“.
- Manche Funktionen haben auch so genannte „schräge Asymptoten“.
- Zum Ableiten einer gebrochen rationalen Funktion brauchen wir die Quotientenregel.
Überprüfe dein Wissen:
Kreuzworträtsel
Zuordnungsübung
Lernstoff
|
|
2.2 Durchgerechnetes Beispiel einer Kurvendiskussion
|

 
|
Kurvendiskussion der gebrochen rationalen Funktion f:
f(x) = x² / ( x+1 )
- Definitionsmenge:
- Wann ist der Nenner = 0?
x + 1 = 0 ⇔ x= -1
Somit ergibt sich für die Definitionsmenge: D = R\{-1}
- Verhalten der Definitionslücke
Beim Einsetzen von -1 in das Bildungsgesetz wird der Nenner = 0, der Zähler = 1.
Daher befindet sich bei x= -1 eine Polstelle (= senkrechte Asymptote) die von der Funktion angenähert wird.
- Schräge Asymptote:
Wir erhalten die schräge Asymptote durch ausführen der Polynomdivision:
x² : (x+1) = x-1 mit Rest r=1
Das heißt, die schräge Asymptote hat die Darstellung y = x-1.
- Nullstellen bestimmen:
Wir setzen die Funktion f(x) = 0.
Das heißt: x² / ( x+1 ) = 0
⇔ x² = 0
⇔ x = 0
Das heißt die Funktion hat eine Nullstelle im Punkt N(0/0)
- Extremwerte bestimmen:
Wir setzen die erste Ableitung der Funktion f'(x) = 0.
Das heißt: (x²+2x) / (x+1)² = 0
Das gilt genau dann wenn: x² + 2x = 0
⇔ x (x+ 2) = 0
Wir erhalten also durch den Produkt-Null-Satz folgende Ergebnisse für x:
x1 = 0
x2 = -2
Durch Rückeinsetzen in die Funktion f(x), erhalten wir folgende Extrema:
E1 = (0/0)
E2 = (-2 / -4)
Um zu sehen ob diese Hoch- oder Tiefpunkte sind, setzen wir nun in die 2. Ableitung von f ein.
f''(x) = 2 / (x+3)³
f''(0) = 2 > 0 ⇒ T(0/0) ist ein Tiefpunkt
f''(-2) = -2 < 0 ⇒ H(-2/-4) ist ein Hochpunkt
- Wendepunkte bestimmen:
Wir setzen die zweite Ableitung f''(x) = 0.
Das heißt: 2 / (x+3)³ = 0
⇔ 2 = 0 ⇒ FALSCHE AUSSAGE
Die Funktion enthält also keine Wendepunkte.
- Tangentensteigungen:
Wir setzen die x-Werte der Nullstell in die erste Ableitung von f ein.
f'(0) = 0
- Graph zeichnen:
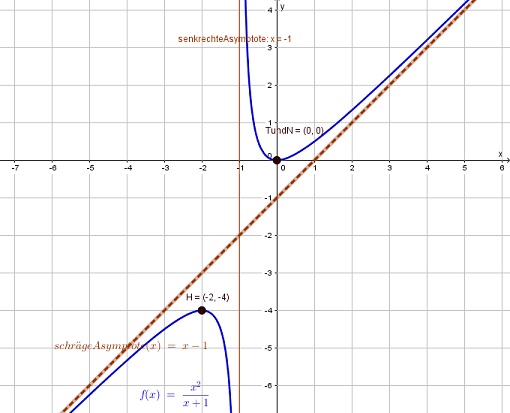
- Monotonieverhalten:
Die Funktion f ist monoton steigend im Intervall: (-∞ ; -2) und (0 ; ∞)
Die Funktion f inst monoton fallend im Intervall: (-2 ; 0)
- Krümmungsverhalten:
Die Funktion f ist positiv gekrümmt im Intervall: (-2 ; ∞)
Die Funktion f ist negativ gekrümmt im Intervall: (-∞ ; -2)
- Symmetrie:
Die Funktion ist nicht Achsen-symmetrisch, da nicht für alle x aus dem Definitionsbereich gilt:
f(x) = f(-x).
Beweis:
Wähle x = 2
f(2) = 1,333333333
f(-2) = 4
- Asymptotisches Verhalten:
Wie verhält sich die Funktion im Unendlichen?
lim (x→ ∞) (x² / ( x+1 )) = "[∞ / ∞]" → das ist nicht definiert.
⇒ durch die Anwendung des Satz von l'Hospital erhalten wir:
lim (x→ ∞ )2x / (1) = +∞
Das heißt, je größer die x-Werte, desto größer auch ihr Funktionswert.
lim (x→ -∞)(x² / ( x+1 )) = "[∞ /- ∞]" → das ist nicht definiert.
⇒ durch die Anwendung des Satz von l'Hospital erhalten wir:
lim (x→ -∞ )2x / 1 = -∞
Das heißt je kleiner die x-Werte, desto kleiner auch ihr Funktionswert.
|
|
2.3 Übungsbeispiel: Kurvendiskussion einer gebrochen rationalen Funktion
|

 

|
Nun seid ihr an der Reihe!
Führt eine vollständige Kurvendiskussion der Funktion
f(x) = (x² − 3x − 4 ) / (x+2)
durch.
Bitte ladet euer Ergebnis auf der vorbereiteten Moodle Platform "3.Einheit" hoch.
Hier
kommt ihr direkt dort hin!
Gutes Gelingen! :)
Hausaufgabe
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



