|
3.1 Lineare Gleichungssysteme in zwei Variablen
|

  

|
Definition:
- Ein lineares Gleichungssystem mit zwei Gleichungen in zwei Variablen hat die Form:
a1*x + a2*y = a0 (a1, a2, a0 ∈ ℜ, a1 und a2 nicht beide 0)
b1*x + b2*y = b0 (b1, b2, b0 ∈ ℜ, b1 und b2 nicht beide 0)
- Ein Zahlenpaar (x/y) heißt Lösung des Gleichungssystems, wenn die reellen Zahlen x und y beide Gleichungen erfüllen.
Eintrag in das Lerntagebuch, Lernstoff
|
|
3.2 Lösungsmethoden für lineare Gleichungssysteme
|

  

|
- Substitutionsmethode (Einsetzungsmethode):
Aus einer Gleichung wird eine Unbekannte durch die andere ausgedrückt.
Der erhaltene Ausdruck wird in die andere Gleichung eingesetz.
I. x+2y = 8 --> x = 8-2y
II. 3x+y = 9
-------------------------------------
in II. einsetzen:
3*(8-2y)+y = 9 --> y = 3, x = 8-2*3 = 2
Lösung: (2/3)
- Eliminationsmethode (Additionsmethode):
Man multipliziert die Gleichungen mit geeigneten Zahlen, sodass beim Addieren der beiden Gleichungen eine Unbekannte wegfällt:
I. x+2y = 8 /*(-3)
II. 3x-y = 9
-------------------------
I. -3x-6y = -24
II. 3x+y = 9 /+
-------------------------
-5y = -15 --> y = 3
In II. einsetzen: 3x+3 = 9 --> x=2
Lösung: (2/3)
- Komparationsmethode (Gleichsetzngsmethode):
Aus beiden Gleichungen wird die gleiche Unbekannte durch die andere ausgedrückt. Anschließend werden die erhaltenen Ausdrücke gleichgesetzt.
I. x+2y = 8 --> x = 8-2y
II. 3x+y = 9 --> x = 3-(1/3)y
----------------------------------
Gleichsetzen: 8-2y = 3-(1/3)y ---> y = 3
Einsetzen in eine der beiden Gleichungen liefert: x = 2
Lösung: (2/3)
Eintrag in das Lerntagebuch, Lernstoff
|
|
3.4 Graphische und rechnerische Ermittlung von Lösungen
|

  
|
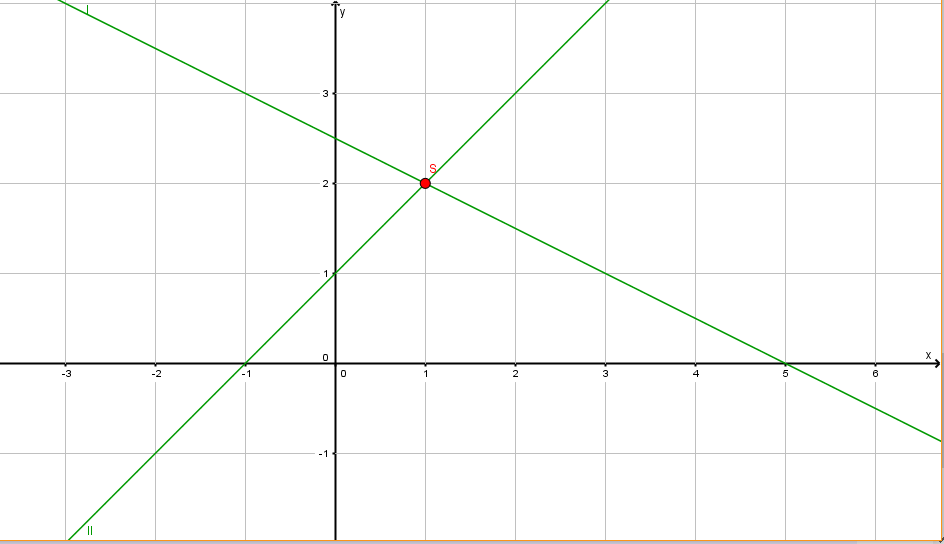
- 1. Beispiel: Löse das folgende lineare Gleichungssystem grafisch und rechnerisch!
I. x + 2y = 5
II.-x + y = 1
Grafische Lösung:
Wir stellen die beiden Gleichungen in expliziter Form dar:
I. x + 2y = 5 --> y = -½x + 5/2
II.-x + y = 1 --> y = x + 1
Da die beiden Geraden verschiedene Steigungen besitzen, mössen sie einander schneiden. Wir stellen sie in einem Koordinatensystem dar.
Der Schnittpunkt S ist der einzige Punkt, der auf beiden Geraden liegt. Das ihm entsprechende Zahlenpaar (1/2) ist somit die einzige Lösung des Gleichungssstems.
Rechnerische Lösung:
Wir lösen das Gleichungssystem mit der Eliminationsmethode.
I. x + 2y = 5
II. -x + y = 1 --> ¦ +
------------------
y = 2; x = 1 --> Lösung: (1/2)
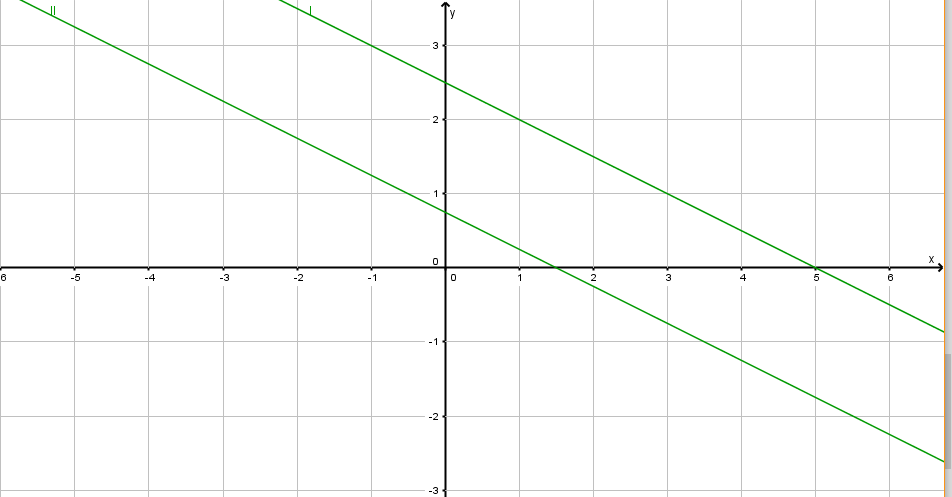
- 2. Beispiel: Löse das folgende Gleichungssystem grafische und rechnerisch!
I. x + 2y = 5
II. 2x + 4y = 3
Grafische Lösung:
Wir stellen die beiden Gleichungen in expliziter Form dar:
I. x + 2y = 5 --> y = -½x + 5/2
II. 2x + 4y = 3 --> y = -½x + ¾
Die beiden Geraden haben die gleiche Steigung, aber verschiedenes d. Sie sind somit parallel, aber nicht zusammenfallend.
Wir stellen sie im Koordinatensystem dar.
Es gibt keinen Punkt, der auf beiden Geraden liegt. Somit besitzt das Gleichungssystem keine Lösung.
Rechnerische Lösung:
Wir lösen das Gleichungssystem mit der Elliminationsmethode.
I. x + 2y = 5 ¦ *(-2)
II. 2x + 4y = 3 --> ¦ +
---------------------------
0 = -7 --> Flasche Aussage !!!
Es gibt kein Zahlenpaar (x/y), das beide Gleichungen erfüllt.
Das Gleichungssystem besitzt daher keine Lösung.
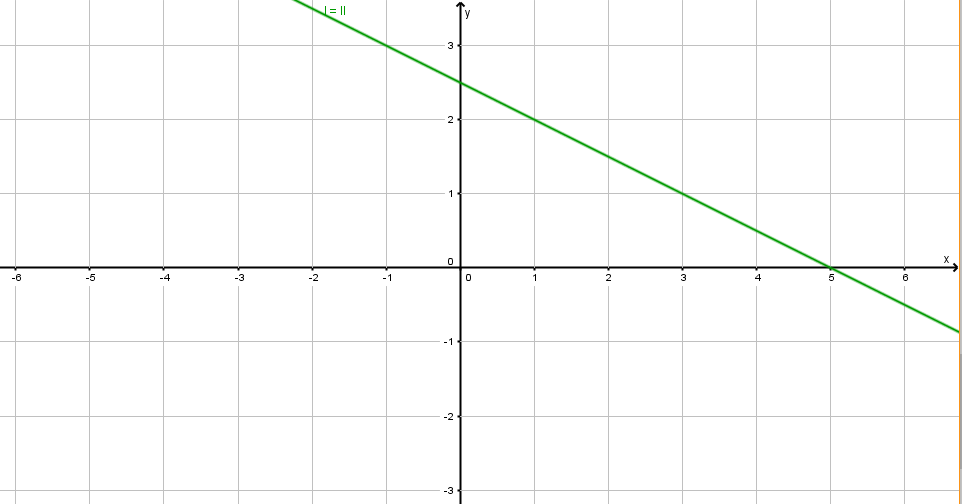
- 3. Beispiel: Löse das folgende linear Gleichungssystem grafisch und rechnerisch!
I. x + 2y = 5
II. 2x + 4y = 10
Grafische Lösung:
Wir stellen die beiden Gleichungen in expliziter Form dar.
I. x + 2y = 5 --> y = -½x + 5/2
II. 2x + 4y = 10 --> y = -½x + 5/2
Die beiden Geraden haben die gleiche Steigung und gleiches d. Sie sind somit parallel und zusammenfallend.
Wir stellen sie im Koordinatensystem dar.
Jeder Punkt auf dieser Gerade entspricht einer Lösung. Somit hat das Gleichungssystem unendlich viele Lösungen
Rechnerische Lösung:
Wir lösen das Gleichungssystem mit der Elliminationsmethode.
I. x + 2y = 5 ¦*(-2)
II. 2x + 4y = 10 --> ¦ +
----------------------------
0 = 0 --> wahre Aussage !!
Jedes Zahlenpaar (x/y), das die 1. Gleichung erfüllt, erfüllt auch die 2. Gleichung.
Das Gleichungssystem besitzt daher unendlich viele Lösungen.
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



