|
2.1 Einleitung
|

 
|
Was ist die Wahrscheinlichkeitsrechnung?
Diese Art zu rechnen erlaubt es uns, vorauszusagen ob ein Ereignis sehr sicher eintreten wird, oder eher nicht.
|
|
2.2 Ein Beispiel
|

  
|
Nimm dir einen Würfel. Nun überlege dir wie hoch stehen deine Chancen, eine 6 zu würfeln?
Die Antwort ist hier einfach:
Es gibt 6 verschiedene Möglichkeiten, wie der Würfel zum Liegen kommen könnte: nämlich alle Zahlen von 1 – 6.
Aber nur eine dieser Zahlen wollen wir tatsächlich würfeln – also ist die Wahrscheinlichkeit eine 6 zu würfeln 1/6.
Anders gesagt dividiert man hier die Anzahl der gewünschten durch die Anzahl der Möglichen.
Wie verändert sich also unsere Rechnung, wenn wir nun würfeln, aber es uns egal ist, ob es eine 5 oder eine 6 ist?
Nun gibt es 2 der 6 Seiten, welche wir uns „wünschen“. Damit ist die Wahrscheinlichkeit 2/6 =1/3.
1/6= 0,166...
1/3= 0,333...
Rechnen wir diese Bruchzahlen aus, sehen wir, dass 1/3 größer ist als 1/6. Damit ist also auch die Wahrscheinlichkeit, eine 5 oder eine 6 zu würfeln größer, als nur eine 6.
Aber das hast du dir sicher schon gedacht.
|
|
2.3 Mensch ärgere dich nicht!
|

 

|
Der blaue Spieler ist am Zug.
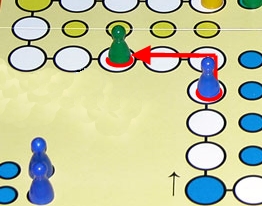
Um den grünen Kegel zu werfen muss er exakt 3 würfeln.
Andererseits will er aber auch nicht höher würfeln als 3, damit er nicht vor den grünen Spieler gerät, und selbst in Gefahr schwebt.
Wie groß ist die Wahrscheinlichkeit, erfolgreich zu sein?
Lösung
|
|
2.4 Die Wahrscheinlichkeiten von mehreren Durchgängen werden multipliziert.
|

  
|
Betrachten wir dazu ein Beispiel:
Wir nehmen an, du gewinnst, wenn du mit einem Würfel eine 6 würfelst.
Wie schon gehört, ist diese Wahrscheinlichkeit = 1/6.
Doch wie sieht das aus, wenn du nun 3 mal hintereinander gewinnen möchtest?
Die Antwort lautet: 1/6 · 1/6 · 1/6 = 1/216 = 0,00462...
Du siehst also, die Wahrscheinlichkeiten werden multipliziert. Dasselbe funktioniert auch hier:
3 verschiedene Spiele hintereinander:
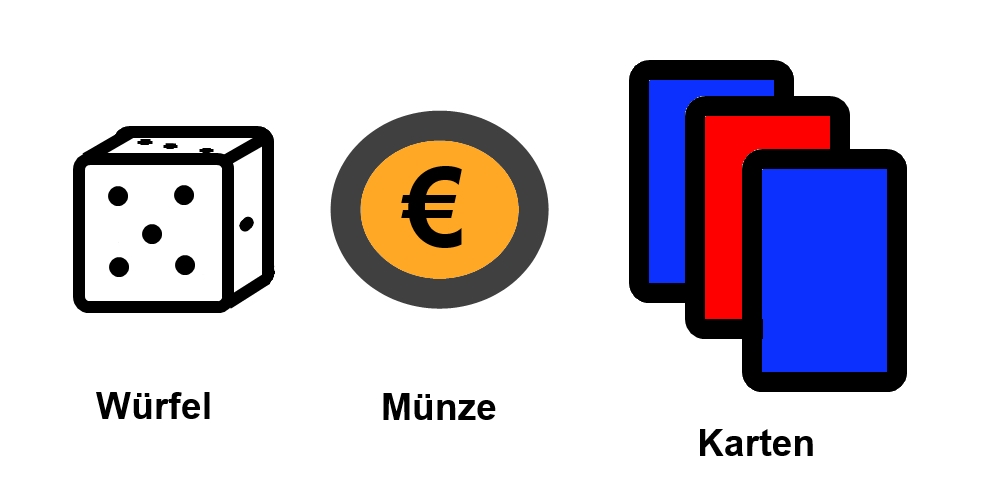
Wie groß ist die Wahrscheinlichkeit, eine 1 zu würfeln, Zahl zu werfen und eine rote Karte zu ziehen?
Lösung
|
|
2.5 Gegenwahrscheinlichkeit
|

 
|
Alle Wahrscheinlichkeiten haben eines gemeinsam: Sie haben eine Gegenwahrscheinlichkeit.
Diese setzt sich so zusammen: Wahrscheinlichkeit + Gegenwahrscheinlichkeit = 1
Das heißt also nur, wenn P(A) die Wahrscheinlichkeit ist, dass A eintritt, dann ist P(¬A) die Wahrscheinlichkeit dass A NICHT eintritt.
Ein Beispiel:
Die Wahrscheinlichkeit, dass eine Feuerwerksrakete normal startet ist 0,98. Damit ist die Gegenwahrscheinlichkeit, also die Wahrscheinlichkeit, dass es zu einer Fehlzündung kommt 1 - 0,98 = 0,02.
¬A wird gesprochen als non A
|
|
2.6 Umrechnung
|

 

|
Wahrscheinlichkeiten werden immer wieder benötigt, um etwas zu veranschaulichen. Zum Beispiel in der Zeitung: "man vermutet bloß 2/3 Wahlbeteiligung". Anders gesagt meint man: eine beliebige Person unserer Stadt wird nur mit 66,6 % Wahrscheinlichkeit wählen gehen.
Wie aber kommt man auf 66,6%?
2/3 = 0,666...
Betrachte einen Würfel:
Die Wahrscheinlichkeit, 1,2,3,4,5 oder 6 zu würfeln ist dann:
1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6 = 1
Wir reden also davon, dass jedes Ergebnis "erwünscht" ist.
Dass irgendeines dieser Ergebnisse eintritt ist zu 100% sicher!
Betrachten wir also diese Tabelle:

Vertiefung
|
|
2.7 Mit und ohne Zurücklegen
|

  
|
Betrachten wir noch einmal das Beispiel aus Kapitel 1.4:
Wir haben 10 Stifte in einer Schachtel und nehmen 3 davon heraus. Ohne es bisher erwähnt zu haben, ist es eigentlich wichtig, dazuzusagen, dass wir diese 3 Stifte "mit einem Griff" herausnehmen. In der Wahrscheinlichkeitsrechnung sagt man auch "ohne Zurücklegen".
Es gibt allerdings auch eine zweite Variante, nämlich "mit Zurücklegen". Damit ist gemeint, dass ich aus meiner Schachtel erst einen Stift herausnehme, wieder zurück hineinlege und erst dann erneut ziehe. Wenn ich also 3 mal ziehe, gibt es hier sogar die Möglichkeit, 3 mal die gleiche Farbe zu erhalten. Natürlich ist diese Wahrscheinlichkeit sehr gering.
Wie groß ist also die Wahrscheinlichkeit, 3 mal einen grünen Stift zu ziehen?
Die Antwort sieht so aus: Von den 20 Stiften die in der Schachtel sind gibt es nur einen grünen - damit ist die Wahrscheinlichkeit den grünen zu ziehen 1/20. Schaffen wir es tatsächlich, dann legen wir ihn aber gleich wieder zurück in die Schachtel, mischen und ziehen erneut - die Wahrscheinlichkeit den grünen zu erhalten ist also wieder dieselbe, genauso wie beim dritten Mal. Also: 1/20 · 1/20 · 1/20 = 1/8000 = 0,000125
Überlegen wir uns die Wahrscheinlichkeiten die Stifte grün, rot und blau zu erhalten:
"ohne Zurücklegen": Hier nehmen wir also mit einem Griff 3 Stifte heraus: 1/20 · 1/19 · 1/18 = 1/6840
"mit Zurücklegen": Hier ziehen wir, legen zurück und ziehen wieder: 1/20 · 1/20 · 1/20 = 1/8000
Hier sehen wir also, ohne zurückzulegen ist die Wahrscheinlichkeit die gewünschten Stifte zu erhalten größer.
Überlege dir selbst:
Wie groß ist die Wahrscheinlichkeit, einen roten und einen blauen Stift zu ziehen, wenn 3 Mal gezogen wird und nicht zurückgelegt wird?
Wie groß ist die Wahrscheinlichkeit, zwei blaue Stifte zu ziehen, wenn 3 Mal gezogen und zurückgelegt wird?
Lösung
|
|
2.8 Mindestens einmal
|

 
|
Ist die Fragestellung:
Nenne die Wahrscheinlichkeit, dass mindestens einmal bei x Durchläufen etwas zutrifft,
dann gilt:
Mindestens Einmal ist Eins minus kein Mal.
Beispiel:
Nenne die Wahrscheinlichkeit, dass bei 3 Mal würfeln mindestens einmal 6 erscheint.
Lösung:
1 - (5/6 · 5/6 · 5/6) = 0,42
|
|
2.9 Beispiele
|

 
|
Beachte bei den kommenden Beispielen:
Ein Laplace Würfel ist ein Würfel, der perfekt ausbalanciert ist, sodass jede seiner Seiten mit der gleichen Wahrscheinlichkeit (nämlich 1/6) erscheint.
Quizfrage 1
Quizfrage 2
Beispiele
Lösungen
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



