Abzählung der Augenzahlen-Summen:
Um zu ermitteln, wieviele Möglichkeiten es gibt, eine vorgegebene
Augenzahlen-Summe k zu erhalten, zeichnen wir
alle möglichen Augenzahlenkombinationen als Punkte in der Zeichebene:
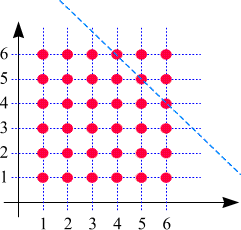
Auf den Achsen sind die Augenzahlen der beiden Würfeln aufgetragen.
Die Menge aller Augenkombinationen, die zu einer gegebenen Augenzahlen-Summe k
führen, wird dargestellt durch alle roten Punkte, die auf der Geraden mit der Gleichung
x + y = k
liegen. (Die blau-strichlierte Linie ist die Gerade
x + y = 10,
die auf ihr liegenden Punkte stellen daher eine Augenzahlen-Summe von 10
dar).
Mit diesem kleinen Trick wird nun klar:
- Es gibt 1 Möglichkeit, die Augenzahlen-Summe 2 zu erzielen.
- Bei jeder Erhöhung der Augenzahlen-Summe um 1 kommt eine Möglichkeit dazu, bis die Summe
7 erreicht.
- Danach fällt bei jeder Verminderung der Augenzahlen-Summe
um 1 eine Möglichkeit weg.
Die Wahrscheinlichkeit für die Augenzahlen-Summe k ergibt sich,
indem die Zahl der Möglichkeiten, sie zu erzielen, durch 36 dividiert wird.

