Größere Schriftzeichen   

Das Geburtstagsproblem:

Die folgende reizvolle Aufgabe zeigt, wie schnell und zielsicher die Formeln der Kombinatorik bei der Berechnung von Wahrscheinlichkeiten genutzt werden können:

Das Geburtstagsproblem:
Am ersten Schultag sitzen in einer Klasse 25 SchülerInnen. Die Lehrperson kennt die Geburtsdaten der SchülerInnen nicht und bietet folgende Wette an: "Wetten, dass zumindest zwei von euch am selben Tag Geburtstag feiern?" Die SchülerInnen wetten dagegen. Wer hat mehr Aussicht, die Wette zu gewinnen?

Um diese Frage entscheiden zu können, muss die Wahrscheinlichkeit, dass zumindest zwei SchülerInnen am selben Tag des Jahres Geburtstag feiern, berechnet werden. Der Einfachheit halber können zwei Idealisierungen gemacht werden: Berechnung:
Wir führen die Berechnung etwas allgemeiner durch: Das Jahr besteht aus n Tagen, und es sind k SchülerInnen anwesend.
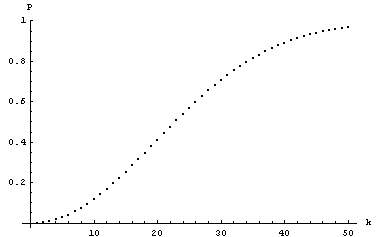
Das Problem entspricht einem Zufallsexperiment, in dem die Namen der k SchülerInnen zufällig und unabhängig voneinander in einen Jahreskalender eingetragen werden. Ein Versuchsausgang ist ein vollständig mit den Namen aller SchülerInnen ausgefüllter Kalender. Alle Versuchsausgänge, die dabei auftreten können, sind gleich wahrscheinlich. Daher handelt es sich um ein Laplace-Experiment. Zur Berechnung der Wahrscheinlichkeiten seiner Ereignisse kann die Formel (4) weiter oben in diesem Kapitel genutzt werden.
Wir berechnen zunächst die Gegenwahrscheinlichkeit, d.h. die Wahrscheinlichkeit w, dass keinerlei gemeinsame Geburtstage auftreten. Die "Zahl der möglichen Fälle" ist die Zahl der Möglichkeiten, k Objekte (die Namen der SchülerInnen) auf n Plätze (Tage) zu verteilen, wobei die k Objekte unterscheidbar sind und jeder Platz mehrere Objekte zugewiesen bekommen darf. In der Sprache dieses Kapitels ist das die Zahl der Möglichkeiten, n Elementen k Schleifen umzubinden, wobei die Schleifen unterscheidbar sind und jedes Element mehrere Schleife bekommen darf. Es handelt sich um eine Variation mit Wiederholung. Daher gilt:

Zahl der möglichen Fälle  =  nk.

Die "Zahl der günstigen Fälle" ist die Zahl der Möglichkeiten, die Verteilung der SchülerInnen-Namen auf die Tage des Jahres so vorzunehmen, dass an jedem Tag höchstens ein Name verzeichnet ist. In der Sprache dieses Kapitels ist das die Zahl der Möglichkeiten, n Elementen k Schleifen umzubinden, wobei die Schleifen unterscheidbar sind und jedes Element höchstens eine Schleife bekommen darf. Es handelt sich um eine Variation ohne Wiederholung. Daher gilt:

Zahl der günstigen Fälle   =     n!
(n − k)! 		 .

Die Wahrscheinlichkeit w ist der Quotient "Zahl der günstigen Fälle/Zahl der möglichen Fälle", daher

w  =     n!
(n − k)!  nk 		 .

Die Wahrscheinlichkeit, dass mindestens zwei SchülerInnen am selben Tag Geburtstag feiern, ist daher gleich

p  =  1 − w.

Setzen wir n = 365 und k = 25 ein, so ergibt sich als Lösung des Geburtstagsproblems mit 25 SchülerInnen (gerundet)

p  =  0.57 .

Mit anderen Worten: Die Lehrperson hat die bessere Chance, die Wette zu gewinnen als die SchülerInnen!

Nachbemerkung:
Dieses Ergebnis ist erstaunlich, aber wahr! Es ist lehrreich, die Wahrscheinlichkeit p für n = 365, aber auch für andere Werte von k zu betrachten. Einige ausgewählte Werte sind (gerundet):

k = Zahl der
 SchülerInnen 
 p = Wahrscheinlichkeit, dass zumindest zwei
 SchülerInnen am selben Tag Geburtstag feiern 
50.027
100.117
180.347
190.379
200.411
210.444
220.476
230.507
240.538
250.569
260.598
270.627
500.970
1000.99999969

Bereits ab einer SchülerInnenzahl von 23 hat die Lehrperson die bessere Chance, die Wette zu gewinnen!

Eine bequemere Übersicht über das schnelle Ansteigen der Wahrscheinlichkeit für gemeinsame Geburtstage gibt eine grafische Darstellung (p als Funktion von k):


Werden die Schalttage berücksichtigt, so ändern sich die Zahlen nur geringfügig. Insbesondere bleibt die SchülerInnenzahl, ab der die Wahrscheinlichkeit für gemeinsame Geburtstage größer als 1/2 ist, bei 23.