Beweis der Multiplikationsregel für Baumdiagramme:
Multiplikationsregel für Baumdiagramme:
Die Wahrscheinlichkeit eines Pfades in einem Baumdiagramm
ist gleich dem Produkt der entlang ihm verzeichneten Wahrscheinlichkeiten.
Beweis:
Gemäß der Definition der Wahrscheinlichkeit, Formel (3) weiter oben in diesem
Kapitel, ist die Wahrscheinlichkeit eines Ereignisses die für eine gegen unendlich strebende
Anzahl n von Durchführungen des betreffenden Zufallsexperiments vorausgesagte relative Häufigkeit
seines Eintretens.
Es sei also ein Zufallsexperiment gegeben und durch ein Baumdiagramm dargestellt.
Wir stellen uns eine sehr große Zahl n von Durchgängen
des Experiments vor. Im Sinne der Definition der Wahrscheinlichkeit stellen
die im Baumdiagramm den Linien zugeordneten Wahrscheinlichkeiten (annähernd)
die Anteile dar, gemäß derer sich die Zahlen der tatsächlich aufgetretenen
Versuchsausgänge an jedem Verzweigungspunkt auf die vorhandenen Möglichkeiten aufteilen.
Dabei ist die Summe der bei jeder Verzweigung auftretenden Anteile
gleich 1.
Nun kommt ein bestimmter Anteil der Versuchsdurchgänge
bis zu einem bestimmten Verzweigungspunkt - bei der Aufteilung auf die von ihm
weiterführenden Linien muss dieser Anteil mit den Anteilen der weiterführenden Linien multipliziert werden.
Auf diese Weise können, ausgehend vom obersten Verzweigungspunkt,
die Anteile der tatsächlich bis zu einer bestimmten Line kommenden
Versuchsdurchgänge ermittelt werden:
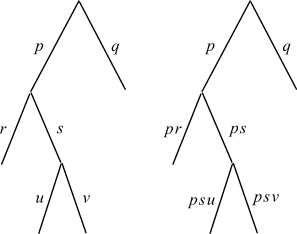
Links ist ein Baumdiagramm mit der üblichen Beschriftung dargestellt.
Die Wahrscheinlichkeiten der einzelnen Teil-Zufallsexperimente sind normiert:
p + q = 1,
r + s = 1 und
u + v = 1.
Rechts sind jene Zahlen eingetragen, die die tatsächlichen Anteile
der Versuchsdurchgänge, die bis zu einer bestimmten Linie kommen, darstellen.
Im Grunde genommen wurde damit nur jedes Teil-Zufallsexperiment an das
jeweils vorhergehende "angeschlossen".
Sie können sich ein Baumdiagramm als ein System von Rohren mit
Verzweigungen vorstellen, durch die Wasser fließt. Die Zahlen
im linken Diagramm bezeichnen die an jedem Verzweigungspunkt auf 1
normierten Aufspaltungs-Anteile. Die Zahlen im rechten Diagramm bezeichnen die
tatsächliche Durchflussmenge durch jede Linie (wobei der Gesamt-Durchfluss
auf 1 normiert ist).
Im Grenzfall einer gegen unendlich strebenden Anzahl von Versuchsdurchgängen
fällt der Zusatz "annähernd" weg, womit
die Multiplikationsregel für Baumdiagramme bewiesen ist.

