Kleine Winkel:
Betrachten wir einen kleinen Winkel α im
Zeigerdiagramm:
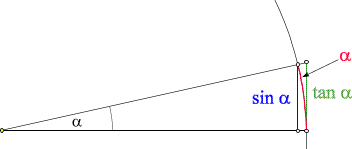
Dann ist
- der Wert von α im Bogenmäß durch die Läge
des roten Kreisbogens (dessen Radius 1 ist) gegeben,
- sin α ist die Länge der
blauen Strecke und
- tan α die Länge
der grünen Strecke.
Ist α sehr klein, dann werden diese drei Lägen
annähernd gleich sein. Genauer ausgedrückt:
Ihre Quotienten
sin(α)/α
und
tan(α)/α
werden umso näher bei 1 liegen, je kleiner α
ist, und durch Verkleinerung von α kommen sie
beliebig nahe an 1 heran.
Diese Argumentation ist zwar kein strenger Beweis, aber sie soll uns genügen, um
intuitiv einzusehen, dass für kleine α und bei
Verwendung des Bogenmaßes
gilt.