Beweis von (29) − Volumen des Parallelepipeds:
Wir verwenden für das Volumen des Parallelepipeds die Formel
V = Grundfläche
× Höhe.
Als Grundfläche betrachten wir das von
a und b
aufgespannte Parallelogramm.
Der Vektor
a
∧b
steht normal auf diese Fläche (ist also parallel zu jener Richtung, in der die Höhe gemessen wird!), und sein
Betrag ist gleich dem Flächeninhalt.
Nun wenden wir die geometrische Definition des Skalarprodukts auf die
Vektoren a∧b
und c an:
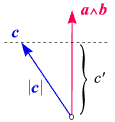
c', die (orientierte) Projektion
von c in die Richtung
von a∧b,
ist gerade (plus oder minus) der Höhe des Parallelepipeds, woraus sich ergibt:
|(a∧b)c| = Grundfläche
× Höhe
= V.
Damit ist (29) bewiesen.