Größere Schriftzeichen   

Höhenschnittpunkt im gleichseitigen Dreieck:

Satz: Der Höhenschnittpukt im gleichseitigen Dreieck teilt jede Höhe im Verhältnis 2:1.

Beweis: Wir bezeichnen gemäß der folgenden Skizze die beiden Abschnitte der Höhe mit x und y:


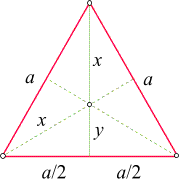
Daher ist h = x + y. Weiters wissen wir bereits, dass

h  =    a 
2
   __
√ 3
 
  (3)

ist. Wir betrachten nun folgendes (hellblaue) rechtwinkelige Dreieck




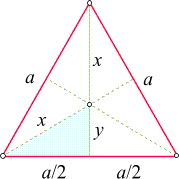
und schreiben für es den Satz von Pythagoras an:

(a/2)2 + y2  =  x2.

Mit y = h − x wird das zu

(a/2)2 + (h − x)2  =  x2.

Den ersten Term können wir durch h ausdrücken, denn aus (3) folgt sofort, dass (a/2)2  =  h2/3 ist. Damit ergibt sich

h2/3 + (h − x)2  =  x2.

Nun kommen nur mehr die Längen h und x vor! Wir fassen diese Beziehung als Gleichung für x auf. Nehmen Sie ein Blatt Papier zur Hand und lösen Sie sie!

Sie sollten das Resultat

x  =  2h/3

erhalten. Mit y = h − x ergibt sich daraus

y  =  h/3.

Daher gilt

x : y  =  2:1,

womit der Satz bewiesen ist.


Nachbemerkung: Es gibt auch andere − durchaus elegantere − Beweise dieses Satzes. So kann beispielsweise dem gegebenen gleichseitigen Dreieck ein auf den Kopf gestelltes (ebenfalls gleichseitiges) Dreieck eingeschrieben werden:




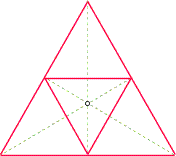
Seine Seitenlänge ist genau halb so groß wie die des ursprüglichen Dreiecks (warum?), und da es zu diesem änhlich ist, besitzt es dieselben Seitenverhältnisse. Gelingt es Ihnen, unseren Satz mit einem einfachen Ähnlichkeitsargument zu beweisen?