Cosinussatz im stumpfwinkeligen Dreieck:
Behauptung: Der Cosinussatz
|
|
(9 ') |
|
|
(9'') |
gilt auch in stumpfwinkeigen Dreiecken.
Beweis: Wir nehmen (ohne Beschränkung der Allgemeinheit) an, dass der
Winkel g stumpf (d.h. größer als 90°) ist:
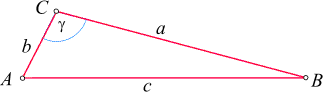
Wir fällen die Höhe auf die Seite b,
die nun außerhalb des Dreiecks liegt:
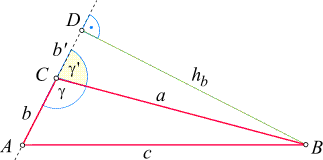
Analog zum spitzwinkeligen Fall setzen wir uns das Ziel, c zu berechnen,
wenn a, b
und g bekannt sind. Dazu verwendet wir folgende zwei
Beziehungen:
- Im rechtwinkeligen Dreieck ABD gilt nach dem Satz von Pythagoras
c2 = hb2 + (b + b')2.
- Im rechtwinkeligen Dreieck CBD schreiben wir die Definitionen von Sinus und Cosinus des
Winkels
g' = 180° - g in der Form
hb = asing'
und
b' = acosg'
an.
Die letzten beiden Beziehungen setzen wir in den Ausdruck für c2
ein und erhalten
c2 = a2sin2g' +
(b +
acosg')2.
Nun gilt, wie im Kapitel Winkelfunktionen besprochen,
sin(180°
- g)
= sing,
cos(180°
- g)
= -cosg,
d.h. sing'
= sing
und
cosg'
= -cosg.
Damit erhalten wir
c2 = a2sin2g +
(b -
acosg)2.
Das ist exakt dieselbe Beziehung, die wir auch im spitzwinkeligen Fall erhalten haben.
Sie führt unmittelbar auf (9).
Die beiden verbleibenden Aussagen (9')
und (9'')
erhalten wir völlig analog zur Argumentation im spitzwinkeligen Fall, indem wir von der (innerhalb des Dreiecks liegenden) Höhe auf die Seite
c ausgehen. Damit ist der Cosinussatz
(9) -
(9'')
auch für stumpfwinkelige Dreiecke bewiesen.