Beispiel für eine nicht-analytische Funktion:
Wir stellen hier ein Beispiel für eine Funktion vor, die beliebig oft differenzierbar ist, sich
aber dennoch nicht in eine Taylorreihe mit Mittelpunkt 0 entwickeln lässt.
Wir definieren die Funktion $f:\mathbb{R}\to\mathbb{R}$ folgendermaßen:
$$f(x)=\left\{\begin{array}{ll}e^{-1/x^2} & \textrm{wenn}\,\,\,\, x\neq 0\\ 0 & \textrm{wenn}\,\,\,\, x=0\end{array}\right.$$
Ihr Graph sieht so aus:
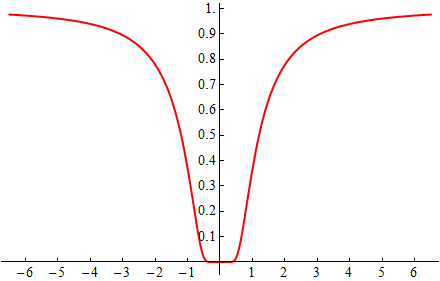
Für $x\to\pm\infty$ strebt sie gegen $e^0 = 1$, für $x\to 0$ strebt sie gegen 0.
An der Stelle $x=0$ ist $e^{-1/x^2}$ nicht definiert, weshalb wir für diesen Fall eigens
den Funktionswert $0$ definiert haben, um $f$ stetig zu machen.
Für $x\neq 0$ ist die Ableitung durch
$$f'(x)=\left(e^{-1/x^2}\right)'=2x^{-3}e^{-1/x^2}$$
gegeben, was für $x\to 0$ gegen $0$ strebt. Die Ableitung an der Stelle $0$ wird in der Form
$$f'(0)=\lim_{\varepsilon\to 0}\,{f(\varepsilon)-f(0)\over \varepsilon} = \lim_{\varepsilon\to 0}\,\,\varepsilon^{-1}e^{-1/\varepsilon^2}=0$$
berechnet, und daher existiert die Ableitungsfunktion $f'$ und ist auf ganz $\mathbb{R}$ stetig.
Auf analoge Weise können alle höheren Ableitungen ermittelt werden. Sie alle existieren, was bedeutet, das
$f$ beliebig off differenzierbar ist.
Aber alle diese Ableitungen verschwinden an der Stelle $0$:
$$f^{(n)}(0)=0$$
für alle $n\in\mathbb{N}_0$. Daraus folgt, dass alle Taylorkoeffizienten
ebenfalls verschwinden:
$$a_n={f^{(n)}(0)\over n!}=0$$
für alle $n\in\mathbb{N}_0$. Die Taylorreihe von $f$ mit Mittelpunkt $0$
lässt sich daher bilden, aber sie ist identisch $0$. Sie stimmt nicht mit $f$
überein! Das bedeutet, dass sich $f$ nicht in eine Taylorreihe entwickeln lässt.

