Loading [MathJax]/extensions/tex2jax.js
Drehung um einen gegebenen Winkel
Die Matrix einer Drehung im Gegenuhrzeigersinn um den Winkel $\alpha$ ist durch
$$R=\left(\begin{array}{cc}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{array}\right)$$
gegeben. Um das zu beweisen, überprüfen wir zunächst, dass die Einheitsvektoren
$e_1$ und $e_2$ in die Achsenrichtungen in gewünschter Weise gedreht werden: Es gilt
$$Re_1=\left(\begin{array}{cc}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{array}\right)\left(\begin{array}{c}1\\0\end{array}\right)=
\left(\begin{array}{c}\cos\alpha\\\sin\alpha\end{array}\right)$$
und
$$Re_2=\left(\begin{array}{cc}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{array}\right)\left(\begin{array}{c}0\\1\end{array}\right)=
\left(\begin{array}{c}-\sin\alpha\\\cos\alpha\end{array}\right)\,{\sf\small.}$$
Unter Verwendung der Definition der Winkelfunktionen Sinus und Cosinus ergibt sich sofort,
dass $Re_1$ bzw. $Re_2$ aus $e_1$ bzw. $e_2$ durch eine Drehung im Gegenuhrzeigersinn um den Winkel $\alpha$
hervorgehen.
Um das Gleiche von einem beliebigen Vektor $x$ zu zeigen, schreiben wir ihn als Linearkombination der
Vektoren $e_1$ und $e_2$ in der
Form $$x=\left(\begin{array}{c}x_1\\x_2\end{array}\right)=x_1e_1+x_2e_2$$
und benutzen die Linearität von $R$:
$$Rx=R(x_1e_1+x_2e_2)=x_1Re_1+x_2Re_2\,{\sf\small.}$$
Das bedeutet, dass sich $Rx$ mit den gleichen Koeffizienten aus $Re_1$ und $Re_2$ zusammensetzt wie
$x$ aus $e_1$ und $e_2$ und daher ebenso wie diese in der gewünschten Weise gedreht wird.
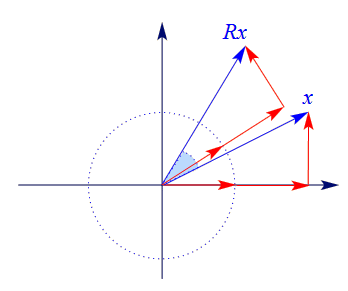
Hier eine Skizze des Sachverhalts für $x_1=2$ und $x_2=1$:
