Orientierter Flächeninhalt

Größere Schriftzeichen

Orientierter Flächeninhalt:

Der orientierte Inhalt einer Fläche ist definiert in Bezug auf eine Orientierung ihres Randes: Stellen wir uns vor, den Rand der Fläche in irgend einer Weise zu durchlaufen (so dass jedes Randstück - abgesehen von möglichen Kreuzungspunkten - nur einmal durchlaufen wird), so wird festgelegt:

Jene zusammenhängenden Teile der Fläche, die links von uns liegen (die also im Gegenuhrzeigersinn, der mathematisch positiven Umlaufrichtung, umrundet werden), tragen mit ihrem Flächeninhalt bei.
Jene zusammenhängenden Teile der Fläche, die rechts von uns liegen (die also im Uhrzeigersinn, der mathematisch negativen Umlaufrichtung, umrundet werden), tragen mit dem Negativen ihres Flächeninhalts bei.

Beim bestimmten Integral

b
ò	f(x) dx
a

definieren wir für stetiges f folgende Orientierung:

Zuerst gehen wir vom Punkt (a, 0) entlang der x-Achse zum Punkt (b, 0), und zwar gleichgültig, ob a < b oder a > b ist,

dann in y-Richtung weiter zum Punkt (b, f(b)),

durchlaufen den gesamten Graphen bis zum Punkt (a, f(a))

und kehren schließlich in y-Richtung wieder zum Ausgangspunkt (a, 0) zurück. Damit ist eindeutig festgelegt, mit welchem Vorzeichen die Flächenstücke zwischen der x-Achse und dem Graphen beitragen. In den meisten Fällen wird die untere Grenze a kleiner als die obere Grenze b sein. In diesem Fall tragen die Flächenstücke oberhalb der x-Achse positiv, jene unterhalb der x-Achse negativ bei:

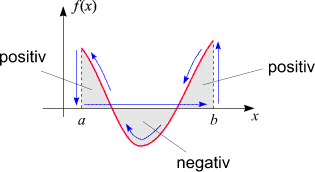
Ist die untere Grenze a größer als die obere Grenze b, ist es gerade umgekehrt.

Diese Regeln werden bei der Anwendung des Hauptsatzes

b
ò	f(x) dx = F(b) - F(a) ,
a

in dem F eine Stammfunktion von f ist, automatisch berücksichtigt. Wir können sogar sagen: Der orientierte Flächeninhalt ist gerade die Art von "Fläche", die diese Formel darstellt.

Für unstetige Integranden existiert zwar kein zusammenhängender Rand, den man entlanglaufen könnte, aber der Begriff des orientierten Flächeninhalts wird sinngemäß auch auf diesen Fall übertragen.