Das bestimmte Integral als kontinuierliche Verallgemeinerung des Mittelwerts und der Summe

Größere Schriftzeichen

Das bestimmte Integral als kontinuierliche Verallgemeinerung des Mittelwerts und der Summe:

Nehmen wir zunächst an, die Funktion f sei auf dem Intervall [a, b] definiert und positiv. Stellen wir die Frage: "Welchen Wert nimmt die Funktion im Intervall [a, b] im Mittel an?"

Das bestimmte Integral

b
∫	f(x) dx
a

stellt den Inhalt der Fläche unter dem Graphen dar. Nun stellen wir dieser Fläche ein flächengleiches Rechteck gemäß folgender Skizze gegenüber:

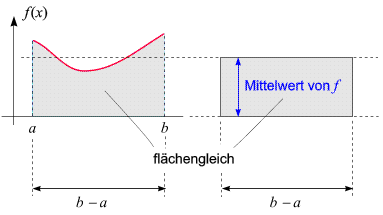
gegenüber. Die horizontale Seitenlänge des Rechtecks ist gleich der Länge des Intervalls, b − a.

Kaum eine Vorgangsweise wäre einleuchtender, als den Mittelwert der Funktion f im Intervall [a, b] als die vertikale Seitenlänge des Rechtecks in der obigen Skizze zu definieren. Da die Rechtecksfläche gleich dem Produkt aus dieser Länge und b − a ist, folgt dann, dass der Mittelwert von f durch

1 b − a	b
	∫	f(x) dx
	a

gegeben ist. Wir können diese Definition als Analogon (oder "kontinuierliche Verallgemeinerung") der Mittelwertsformel

1 n	n
	Σ	c_j
	j = 1

für n Zahlen c₁, c₂, ... c_n betrachten (siehe das Kapitel Beschreibende Statistik (in Vorbereitung)). Das bestimmte Integral wird damit zu einer kontinuierlichen Verallgemeinerung des Begriffs der Summe.

Genauso, wie manche der Zahlen c_j null oder negativ sein können, können wir die Beschränkung auf positives f fallen lassen und obige Formel auch in diesem Fall verwenden. Der so definierte Mittelwert einer Funktion in einem Intervall hat gewisse Eigenschaften, die man von einem Mittelwert erwartet:

Ist f(x) ≥ 0 für alle x∈[a, b], so ist auch der Mittelwert von f größer-gleich 0.
Der Mittelwert von f ist nie kleiner als das Minimum von f in [a, b].
Der Mittelwert von f ist nie größer als das Maximum von f in [a, b].
Ist f(x) = K für alle x∈[a, b], d.h. f eine konstante Funktion, so ist der Mittelwert von f gleich dieser Konstanten K.

Beweisen Sie als Übungsaufgabe die letzte dieser Aussagen!

Im Gegensatz zur Gründerzeit der Integralrechnung, für die das Flächeninhaltsproblem im Vordergrund stand, setzt die moderne Theorie der Integration (die Maßtheorie) bei der Idee des "Mittelwerts einer Funktion" an und versucht, diese Idee für möglichst große Klassen unstetiger (d.h. schnell variierender) Funktionen und für Funktionen, die auf anderen Mengen als den reellen Zahlen definiert sind, zu realisieren.