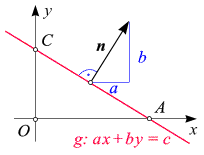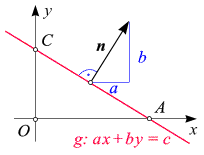Beweis von (13)

Größere Schriftzeichen

Beweis von (13):

Satz: Sei g die durch die Gleichung

ax + by = c

(11)

beschriebene Gerade, wobei wir annehmen, dass zumindest einer der Koeffizienten a und b ungleich 0 ist. Dann gilt:

Gehen wir von einem beliebigen Punkt

um a in die x-Richtung (d.h. nach rechts oder links, je nach dem Vorzeichen von a) und

um b in die y-Richtung (d.h. nach oben oder unten, je nach dem Vorzeichen von b),

so haben wir uns insgesamt in eine Richtung normal auf die Gerade g bewegt.

(13)

Beweis (ohne Vektoren):

Wir führen den Beweis zunächst für den Fall, dass a, b und c positiv sind und haben das Dreieck, das die Gerade g mit den Koordinatenachsen bildet, in der rechten Skizze ein bisschen vergrößert dargestellt:

Wir zerlegen den Beweis in drei Schritte:

Die Längen der Katheten des großen Dreiecks OAC, d.h. die Achsen-Abschnitte OA und OC, können wir zunächst mit Hilfe der Geradengleichung (11) ermitteln: Die Länge OA ist genau die x-Koordinate von A, d.h. jenes Punktes, in dem g die x-Achse schneidet. Um sie zu finden, setzen wir in (11) y = 0 ein, lösen nach x auf und erhalten x = c/a als die gesuchte Länge OA. In analoger Weise finden wir OC = c/b. Damit sind die Katheten des großen Dreiecks bekannt.
Als nächstes bemerken wir, dass das große Dreieck OAC mit dem kleineren Dreieck OAB zwei gleiche Winkel besitzt (jenen bei A und einen rechten). Da die Winkelsumme in allen Dreiecken gleich ist, stimmen die zwei Dreiecke in allen Winkeln und folglich in allen Längenverhältnissen überein. Genau betrachtet, ist OAB eine gespiegelte und geschrumpfte Version von OAC.
Das gelbe Dreieck hat nun seinerseits mit OAB zwei Winkel gemeinsam (jenen bei O und einen rechten) und besitzt daher ebenfalls die gleichen Längenverhältnisse. Damit finden wir b'/a' = (c/a)/(c/b) = b/a. Die entlang der Strecke OB verlaufende (auf g normal stehende) Gerade hat daher den Anstieg b/a. Da dieser mit dem Anstieg der durch den Richtungspfeil n definierten Geraden (linke Skizze) identisch ist, steht n normal auf g.

Damit ist (13) für den Fall bewiesen, dass a, b und c positiv sind. Die ausständigen Fälle sind:

a, b und sind von 0 verschieden, haben aber andere Vorzeichen:
Diese Fälle können völlig analog wie oben bewiesen werden.
Ist c = 0 oder c < 0, hilft ein kleiner Trick: Indem in der Geradengleichung (11) c beliebig verändert, a und b aber gleich gelassen werden, entsteht eine zu g parallele Gerade. (Warum?) Damit kann dieser Punkt auf den vorigen zurückgeführt werden, indem beispielsweise c = 1 gesetzt wird.

Beweis mit Vektoren:

Indem einige einfache Tatsachen über Vektoren (insbesondere über das so genannte "Skalarprodukt von Vektoren") verwendet werden, kann der Beweis erheblich verkürzt werden. Wir werden diesen Blickwinkel im zweiten Geometrie-Kapitel kennen lernen.