| (1) |
| (2) |
 Nun hat der Zähler aber für x = 1
einen von Null verschiedenen Wert, nämlich 2, während der Nenner dort Null wird.
Daher besitzt die Funktion bei x = 1
eine Unendlichkeitsstelle (Polstelle). Der (größtmögliche) Definitionsbereich ist durch
Nun hat der Zähler aber für x = 1
einen von Null verschiedenen Wert, nämlich 2, während der Nenner dort Null wird.
Daher besitzt die Funktion bei x = 1
eine Unendlichkeitsstelle (Polstelle). Der (größtmögliche) Definitionsbereich ist durch
| (3) |
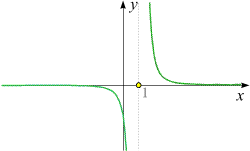 Damit ist klargelegt, was für die Unendlichkeit bei x = 1
verantwortlich ist: die dritte Potenz von
Damit ist klargelegt, was für die Unendlichkeit bei x = 1
verantwortlich ist: die dritte Potenz von
| (4) |
| (5) |