Größere Schriftzeichen   

Exkurs:
Polynome, ihre Nullstellen und Graphen

  Inhalt:  
Definitionsbereich und Stetigkeit

Da Polynome keine Unendlichkeitsstellen besitzen, können sie immer auf ganz R definiert werden. Daher fassen wir jedes Polynom als Funktion  R → R  auf. Jede Polynomfunktion ist stetig, d.h. ihr Graph ist eine zusammenhängende Kurve.

 
Nullstellen − erster Überblick

Die Nullstellen eines Polynoms p sind die Lösungen der Gleichung

p(x)   =   0.
(1)

Sie für ein gegebenes Polynom zu finden, gehört zu den "klassischen" Problemen, die zur Entwicklung der modernen Mathematik geführt haben. Ist p ein Polynom der Ordnung m, so bedeutet das, eine Gleichung m-ter Ordnung zu lösen, was nur für m = 1 und 2 eine leichte Sache und ab m = 5 im allgemeinen Fall auf exaktem Weg gar nicht möglich ist.

Um sich eine erste Orientierung über die Nullstellen eines Polynoms zu verschaffen, ist es ratsam, sich den Graphen anzusehen (z.B. mit Hilfe des Funktions-Plotter). Falls Sie die Nullstellen exakt angeben sollen (oder wollen), ist das allerdings kein Ersatz für die Berechnung!

 
Nullstellen − allgemeine Theorie

Wir formulieren und beweisen drei Sätze, die die Analyse von Polynomen erleichtern.
 
Satz 1: Abspaltung eines Linearfaktors
Sei p eine Polynomfunktion mit Nullstelle x0. Dann kann p in der Form

p(x)   =   (x − x0)  q(x)
(2)

geschrieben werden, wobei h ebenfalls ein Polynom ist. Das bedeutet, dass ein Polynom mit Nullstelle x0 den "Linearfaktor" x − x0 enthält. Im Fachjargon heißt das oft: "Die Nullstelle (genauer: der Linearfaktor) wird abgespaltet".
Beweis:
(Wenn Sie sich nicht in die Sache vertiefen wollen, können Sie ihn überspringen. Er sei Ihnen aber dennoch ans Herz gelegt, da er ein Rechenverfahren, das Sie vielleicht in der Praxis brauchen werden, beinhaltet).

Wir zeigen die Art der Beweisführung anhand eines Beispiels und argumentieren dann, dass sie sich auf den allgemeinen Fall übertragen lässt. Nehmen wir zuerst an, unsere Polynomfunktion sei

p(x)   =   2x3 + 2x2 − 20x + 16.
(3)

Sie besitzt bei x0 = 2 eine Nullstelle. (Rechnen Sie nach, dass p(2) = 0 ist!) Der Satz behauptet die Existenz eines Polynoms q, das die Identität

2x3 + 2x2 − 20x + 16   =   (x − 2)  q(x)
(4)

erfüllt. Können wir es finden? Ja, und das ist gar nicht so schwierig! q muss ein Polynom zweiter Ordnung sein, ansonsten könnte die höchste Potenz der rechten Seite von (4) nicht mit jener der linken Seite, nämlich 2x3, übereinstimmen. Wir kennen q (noch) nicht, wissen aber, dass jedes Polynom zweiter Ordnung von der Form

q(x)   =   a2x2 + a1x + a0
(5)

ist, wobei die Koeffizienten a0, a1 und a2 reelle Zahlen sind. Gleichung (4) wird manchmal als "Ansatz" (für q) bezeichnet.

Nun setzen wir (4) in (5) ein und erhalten

2x3 + 2x2 − 20x + 16   =   (x − 2)  (a2x2 + a1x + a0)
(6)

Die rechte Seite wird ausmultipliziert und vereinfacht:

2x3 + 2x2 − 20x + 16   =   a2x3 + (a1 − 2a2)x2 + (a0 − 2a1)x − 2a0 .
(7)
Nun steht auf beiden Seiten dieser Beziehung ein Polynom. Diese beiden Polynome sollen gleich sein. Wir setzen also die (bekannten) Koeffizienten der linken Seite gleich den entsprechenden (unbekannten) Koeffizienten der rechten Seite:

2   =   a2       
(8)
   2   =   a1 − 2a2
(9)
−20   =   a0 − 2a1
(10)
16   =   −2a0   
(11)

Das ist ein System von Gleichungen, das wir jetzt nach den unbekannten Koeffizienten aufzulösen versuchen. (8) sagt uns unmittelbar, dass a2 = 2 ist. Damit impliziert (9), dass a1 = 2a2 + 2 = 6 ist. (10) ergibt a0 = 2a1 − 20 = 2 × 6 − 20 = −8.
Einschub, der später wichtig sein wird:
(Wenn Sie nur am Rechenverfahren, nicht aber am allgemeinen Beweis interessiert sind, können Sie ihn überspringen).

Wir haben nun alle Koeffizienten erhalten, aber es ist noch eine Gleichung übrig! Gleichung (11) liefert keine neue Information, sondern ist identisch erfüllt: 16 = −2 × (−8). Das ist kein Zufall: Wir hätten diese Gleichung völlig ignorieren können, denn sie muss identisch erfült sein. Stellen wir uns vor, wir setzen die aus (8) bis (10) erhaltenen Werte für die Koeffizienten in (7) ein. Dann steht auf jeder der beiden Seiten von (7) ein Polynom. Die Gleichungen (8) bis (11) besagen, dass diese beiden Polynome in allen höheren Ordnungen von x übereinstimmen. Sie unterscheiden sich also höchstens in einer additiven Konstante, denn die nicht beachtete Gleichung (11) ist gerade für die "nullte" Ordnung in x zuständig. Mit anderen Worten: Die Differenz von linker und rechter Seite in (7) ist eine Konstante. Andererseits haben beide Polynome bei x0 = 2 eine Nullstelle (die linke Seite laut Voraussetzung, die rechte Seite, weil sie mit der rechten Seite von Gleichung (6) identisch ist). Aber die Differenz zweier Polynome, die eine gemeinsame Nullstelle besitzen, kann keine von Null verschiedene Konstante sein! Daher sind die beiden Seiten von (7) tatsächlich gleich, und Gleichung (11) kann ignoriert werden.
Setzen wir die erhaltenen Werte in (5) ein, so erhalten wir das gesuchte Polynom q:

q(x)   =   2x2 + 6x − 8.
(12)

Es erfüllt die Identität (4). Wir können das noch einmal checken, um Rechenfehler auszuschließen:

(x − 2)  (2x2 + 6x − 8)   =   2x3 + 2x2 − 20x + 16.
(13)

Damit ist der Satz anhand des Polynoms (3) überprüft. Funktioniert dieses Verfahren für jedes Polynom p und jede seiner Nullstellen? Wenn ja, und wenn wir das auch zeigen können, dann haben wir auch den Satz in seiner Allgemeinheit bewiesen.

Ja, das Verfahren funktioniert immer! Überlegen Sie selbst, dass wir für jedes Polynom p zu einem System von Gleichungen analog zu (8) bis (11) gelangen. Ist p von höherer Ordnung, so ist dieses System entsprechend größer, da q dann auch mehr Koeffizienten besitzt. Genau wie in unserem Beispiel können diese Gleichungen der Reihe nach gelöst und alle alle Koeffizienten bestimmt werden, bis zuletzt eine Gleichung übrig bleibt. Diese muss aber − entsprechend der Argumentation unseres Einschubs, der sich wortwörtlich auf den allgemeinen Fall überträgt − identisch erfüllt sein.

Damit ist Satz 1 bewiesen.
Beachten Sie: Die Beweisführung ist nicht rein akademisch, sondern bringt ein Verfahren ans Licht, das wir benutzen können, um das in (2) auftretende Polynom q zu berechnen!

Bemerkung: Dass sich eine Nullstelle eines Polynoms als Linearfaktor bemerkbar macht, ist uns nicht ganz neu: Wir sind im Zusammenhang mit quadratischen Gleichungen (Polynomen zweiter Ordnung) und dem "Vietaschen Satz" im Kapitel Gleichungen schon darauf gestoßen.
 
Satz 2: Abspaltung aller Linearfaktoren
Sei p eine Polynomfunktion mit Nullstelle x0. Dann kann p in der Form

p(x)   =   (x − x0)n h(x)
(14)

geschrieben werden, wobei n eine natürliche Zahl und h ein Polynom mit h(x0) ≠ 0 ist.
Beweis:

Er ist nun ganz einfach. Gemäß Satz 1 kann p in der Form

p(x)   =   (x − x0)  q(x)
 

geschrieben werden. Die Ordnung von q ist kleiner als jene von p.
  • Ist q(x0) = 0, so wenden wir Satz 1 auf q an, um einen weiteren Linearfaktor abzuspalten: q(x)  =  (x − x0) r(x) für ein Polynom r, daher p(x)  =  (x − x0)2 r(x). Die Ordnung von r ist kleiner als jene von q.
  • Ist r(x0) = 0, so wenden wir den Satz wieder an, usw.
Da die Ordnung der dabei auftretenden Polynome (p, q, r,...) bei jedem Schritt abnimmt, kommt das Verfahren nach endliche vielen Schritten zum Stillstand − spätestens, wenn das konstante Polynom (nullter Ordnung) erreicht ist. Irgendwann tritt ein Polynom h auf, für das h(x0) ≠ 0 ist. Mit anderen Worten: Der Linearfaktor x − x0 wird so oft abgespaltet wie möglich. n ist die Zahl der Schritte, die der gesamte Prozess benötigt.

Damit ist Satz 2 bewiesen.
Nachbemerkung 1: Die Nullstelle x0 tritt in (14) "n mal" als Linearfaktor auf. Daher wird sie auch "Nullstelle der Vielfachheit n" genannt.

Nachbemerkung 2: Aus Satz 2 folgt unmittelbar:
 
Jede Nullstelle eines Polynoms hat eine wohldefinierte Ordnung.      
Begründung: Für x ≈ x0 können wir in (14)  h(x)  ≈  h(x0) schreiben und kürzen dies als c ab. Damit wird das Verhalten von p nahe der Nullstelle x0 durch

p(x)   ≈   c(x − x0)n
(15)

mit c ≠ 0 beschrieben. So ist aber gerade eine Nullstelle n-ter Ordnung definiert. Die Ordnung einer Nullstelle ist daher gleich ihrer Vielfachheit. Hier einige für Nullstellen verschiedener Ordnung.
 
Satz 3: Zahl der Nullstellen
Ein Polynom der Ordnung m besitzt höchstens m Nullstellen.            
Beweis:

Hat ein gegebenes Polynom p der Ordnung m eine Nullstelle x1, so werden zunächst gemäß Satz 2 alle mit ihr verbundenen Linearfaktoren abgespaltet: p(x)  =  (x − x1)n h(x) mit h(x1) ≠ 0. Falls h eine andere Nullstelle x2 besitzt, so wird mit h genauso verfahren, was eine Abspaltung der Form p(x)  =  (x − x1)n (x − x2)k s(x) mit s(x1) ≠ 0 und s(x2) ≠ 0 zur Folge hat. Das Verfahren wird so lange fortgesetzt, bis ein Produkt aus Linearfaktoren und ein Polynom, das überhaupt keine Nullstelle hat, resultiert. Da die Ordnung der dabei auftretenden Polynome (p, h, s,...) bei jedem Schritt abnimmt, kommt das Verfahren nach höchstens m Schritten zum Stillstand, und alle (höchstens m) Nullstellen sind gefunden.

Damit ist Satz 3 bewiesen.
Geometrisch besagt er:
 
Der Graph einer Polynomfunktion m-ter Ordnung kann die x-Achse höchstens 
m mal schneiden.

Wir können diese Aussage leicht verallgemeinern:
 
Der Graph einer Polynomfunktion m-ter Ordnung kann jede beliebige Gerade  
höchstens m mal schneiden.

(Der Beweis ist einfach, wenn Satz 3 verwendet wird. Versuchen Sie es!)

Hier ein Beispiel:
Der gezeigte Graph schneidet jede Gerade höchstens drei mal (eine solche ist eingezeichnet). Es handelt sich daher um ein Polynom von mindestens dritter Ordnung.

 
Nullstellen berechnen

Wollen wir die Nullstellen eines Polynoms der Ordnung m berechnen, so führt der Fall m = 1 auf eine lineare, der Fall m = 2 auf eine quadratische Gleichung. Diese beiden Probleme sind vollständig gelöst (siehe das Kapitel Gleichungen), und wir brauchen über sie kein Wort mehr zu verlieren.

Interessanter ist der Fall m = 3, d.h. das Lösen einer kubischen Gleichung. Wie zeigen hier kein allgemeines Verfahren, sondern besprechen den Fall, daß eine Nullstelle x0 bekannt ist. (Sie könnte erraten worden sein, eventuell nach Betrachtung des Graphen). Satz 1 besagt, dass vom gegebenen Polynom p der Linearfaktor x − x0 abgespaltet werden kann, und die Beweisführung, die wir eingeschlagen haben, liefert uns ein Verfahren, den zweiten Faktor q zu berechnen.

Wir illustrieren es in aller Kürze noch einmal anhand des Beispiels

p(x)   =   2x3 + 5x2 − 4x − 3,
(16)

von dem die Nullstelle x0 = −3 erraten worden ist. (Rechnen Sie nach, dass p(−3) = 0 ist!) Nach Satz 1 gibt es ein Polynom q (zweiter Ordnung), für das

2x3 + 5x2 − 4x − 3   =   (x + 3)  q(x)
(17)

gilt. Wir machen für q den Ansatz

q(x)   =   a2x2 + a1x + a0
(18)

und setzen diesen in (17) ein:

2x3 + 5x2 − 4x − 3   =   (x + 3) (a2x2 + a1x + a0)
(19)

Wir multipliziern die Klammern auf der rechten Seite aus und vereinfachen:

2x3 + 5x2 − 4x − 3   =   a2x3 + (a1 + 3a2)x2 + (a0 + 3a1)x + 3a0 .
(20)
Die beiden Seiten dieser Gleichung müssen (für jede Potenz von x) übereinstimmen. Das ergibt vier Gleichungen

2   =   a2       
(21)
   5   =   a1 + 3a2
(22)
 −4   =   a0 + 3a1
(23)
−3   =   3a0,     
(24)

die der Reihe nach gelöst werden können: a2 = 2, a1 = −1 und a0 = −1. In (18) eingesetzt wird

q(x)   =   2x2 − x − 1,
(25)

womit das gegebene Polynom − siehe (17) − als

2x3 + 5x2 − 4x − 3   =   (x + 3) (2x2 − x − 1)
(26)

geschrieben werden kann. Dieser Ausdruck kann nur dann Null sein, wenn einer der beiden Faktoren verschwindet: Damit sind alle Nullstellen des Polynoms (16) ermittelt.

Wollen Sie ein Polynom dritter (oder höherer) Ordnung analysieren, von dem keine Nullstelle (exakt) erraten werden kann, so haben Sie noch einige andere Möglichkeiten:

Wir wenden uns nun einigen globalen Eigenschaften von Polynomen zu. Sie sind unter anderem dann hilfreich, wenn der Verlauf des Graphen eines Polynoms verstanden werden soll.

 
(Anti-)Symmetrie

Manche Polynomfunktionen sind symmetrisch, manche sind antisymmetrisch und manche sind keins von beiden. Den Schlüssel zu einer allgemeinen Charakterisierung des Symmetrieverhaltens liefern die Identitäten

(−x)n   =   xn      falls n gerade ist,   
(28)
(−x)n   =   −xn     falls n ungerade ist.
(29)

Die Potenzfunktion xn ist also für gerades n symmetrisch und für ungerades n antisymmetrisch. Ersetzen wir in einem gegebenen Polynom x durch −x, so bleiben die Koeffizienten aller Potenzen mit geradem Exponenten gleich, während die Koeffizienten aller Potenzen mit ungeradem Exponenten das Vorzeichen wechseln. Daraus ergibt sich:
 
  • Ein Polynom ist genau dann symmetrisch, wenn es nur Potenzen mit geraden Exponenten enthält.
    Beispiel: 3x4 + 2x2 − 5
     
  • Ein Polynom ist genau dann antisymmetrisch, wenn es nur Potenzen mit ungeraden Exponenten enthält.
    Beispiel: −4x3 + 5x

Hier zwei Beispiele:

 
Asymptotisches Verhalten

Wir kommen nun zum Verhalten einer Polynomfunktion für x → ±∞, d.h. zum Aussehen des Graphen für Bereiche großer |x|.
 
Für x → ±∞ dominiert der Beitrag mit dem größten Exponenten    
(oder, wie man auch sagt, die "höchste Potenz" von x oder der "führende Term").

Damit ist eine wichtige globale Eigenschaft des Graphen eines Polynoms bereits ohne Rechnung sichergestellt.

Sehen wir uns anhand des Beispiels

p(x)  =  −2x3 + 3x2 − 1
(30)

an, was damit gemeint ist: Der Beitrag mit dem größten Exponenten (der "führende Term") ist −2x3. Ist x (oder −x) sehr groß, so ist dieser Term größer als alle anderen Beiträge zusammengenommen, d.h. größer als 3x2 − 1. Für |x| → ∞ verhält sich p(x) näherungsweise wie −2x3.
Warnhinweis: Das bedeutet nicht, dass die Differenz zwischen p(x) und −2x3 im Unendlichen immer kleiner wird (denn diese ist ja das quadratische Polynom 3x2 −1). Aber es bedeutet, dass diese Differenz im Vergleich zu p(x) gegen Null strebt.
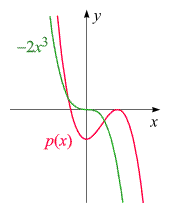Der Graph von p(x) sieht daher "von großer Entfernung aus betrachtet" ähnlich wie jener von −2x3 aus. Wichtig ist: Er kommt aus dem Unendlichen von "links oben" und fällt (was auch immer er dazwischen macht) nach "rechts unten" ins Unendliche ab: Sehen Sie sich die Graphen von p(x) und −2x3 im Funktions-Plotter an und "zoomen" Sie sich heraus, um die Situation "aus großer Entfernung zu betrachten"!

Nebenbei ergibt sich ein äußerst interessantes Resultat: Da p (wie jede Polynomfunktion) stetig ist, ist der Graph eine zusammenhängende Kurve. Daher muss er irgendwo die x-Achse schneiden: p besitzt eine Nullstelle!

Wir haben diese letzte Erkenntnis ganz ohne Rechnung erhalten, und sie hängt lediglich damit zusammen, dass die Ordnung von p (d.h. der höchste auftretende Exponent, der für das Verhalten im Unendlichen verantwortlich ist) eine ungerade Zahl ist (nämlich 3): Wir können also ganz allgemein formulieren:
 
Ein Polynom ungerader Ordnung besitzt (zumindest) eine Nullstelle.    

Zum Thema "Asymptotisches Verhalten" gehört die Frage: Können Polynomfunktionen Asymptoten haben? Da für das Verhalten im Unendlichen die höchste Potenz ausschlaggebend ist, gelangen wir leicht zu einer Klassifizierung:  
Sonstige globale Eigenschaften

Periodizität: Polynome sind nicht periodisch (ausgenommen der triviale Fall der konstanten Funktionen, für die jede reelle Zahl eine Periode ist).

Monotonie: Polynome gerader Ordnung ≥ 2 wechseln ihr Monotonieverhalten, sind also in manchen Bereichen streng momoton wachsend, in anderen Bereichen streng monoton fallend. Polynome erster Ordnung sind, je nach dem Vorzeichen des Koeffizienten von x, streng monoton wachsend (+) oder fallend (−). Polynome ungerader Ordnung ≥ 3 können (müssen aber nicht) ein einheitliches Monotonieverhalten haben.

Konvexitätsverhalten: Polynome zweiter Ordnung sind, je nach dem Vorzeichen des Koeffizienten von x2, konvex ("nach oben offen", für +) oder konkav ("nach unten offen", für −). Polynome ungerader Ordnung ≥ 3 wechseln ihr Konvexitätsverhalten, sind also in manchen Bereichen konvex, in anderen Bereichen konkav. Polynome gerader Ordnung ≥ 4 können (müssen aber nicht) ein einheitliches Konvexitätsverhalten haben.

Unendlichkeitsstellen: Als Funktionen, die auf ganz R definiert sind, besitzen Polynome keine Unendlichkeitsstellen, daher auch keine Pole.

Beschränktheit: Diese hängt eng mit dem asymptotischen Verhalten (siehe oben) zusammen. Polynome gerader Ordnung ≥ 2 sind, je nach dem Vorzeichen des Beitrags mit dem größten Exponenten, nach unten (+) oder nach oben (−) beschränkt. Polynome ungerader Ordnung sind weder nach oben noch nach unten beschränkt. Die einzigen Polynome, die nach oben und nach unten beschränkt sind, sind jene nullter Ordnung (d.h. die konstanten Funktionen).