Falls die Ableitung g'(x0) von Null verschieden ist, ist die Regel intuitiv sehr einfach zu verstehen. In diesem Fall ist die rechte Seite von (10) durch f '(x0)/g'(x0) gegeben. Wir ziehen diesen Fall daher vor und argumentieren anhand einer Skizze:

In einer kleinen Umgebung von x0 können f und g durch lineare Funktionen approximiert werden, deren Graphen die Anstiege f '(x0) und g'(x0) haben:
|
Durch Division dieser beiden Näherungsausdrücke ergibt sich unmittelbar, dass
|
Lassen wir x gegen x0 streben, so wird diese Beziehung immer genauer, woraus sich
|
ergibt. Das ist aber genau die Regel (10) für den betrachteten Spezialfall.
Wir setzen voraus, dass der Grenzwert auf der rechten Seite von (10) existiert. Damit das möglich ist, muss g' an allen Stellen eines Intervalls
|
Für jedes Glied
|
Einschub ("Verallgemeinerter Mittelwertsatz"): Sei h die durch
definierte Funktion. Beachten Sie, dass sie von der einfachen Struktur gilt, d.h. dass sie an den Rändern dieses Intervalls verschwindet. Jede stetig differenzierbare Funktion, für die das gilt, muss an irgendender Stelle zwischen den Rändern 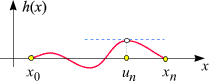
Demnach gibt es eine Zahl un zwischen x0 und xn, für die gilt. Unter Verwendung der obigen Definition von h ergibt sich unmittelbar, dass die Aussage
annimmt. Zusammengefasst: Es existiert eine Zahl un zwischen x0 und xn, für die diese Beziehung gilt. Diese Aussage wird auch als "verallgemeinerter Mittelwertsatz" bezeichnet. Sie gilt ganz allgemein für jedes Paar von stetig differenzierbaren Funktionen. Wegen
an. |
Der Rest des Beweises ist im Grunde genommen recht einfach: Wählen wir eine beliebige Folge (xn), so konvergiert auch die aus den oben konstruierten Zahlen un bestehende Folge, deren Elemente ja zwischen x0 und xn liegen, gegen x0. Folglich konvergiert die aus den Zahlen f '(un)/g'(un) bestehende Folge ebenfalls gegen c. Da aber
|
Das gilt für jede unserer Folgen (xn), was genau die Aussage darstellt, dass die linke Seite von (10) gegen c konvergiert. Damit ist Formel (10) bewiesen.