1. Definition
Wir betrachten die Funktion F(x,y) in der Umgebung U eines Punktes (
![x[0], y[0]](images_fsv3/function_sev_var31.gif) ) und bilden den Grenzwert
) und bilden den Grenzwert
![limit((F(x,y[0])-F(x[0],y[0]))/(x-x[0]),P = P[0])](images_fsv3/function_sev_var32.gif) . Wenn dieser Grenzwert existiert, nennt man ihn die partielle Ableitung der Funktion F(x,y) nach x im Punkte
. Wenn dieser Grenzwert existiert, nennt man ihn die partielle Ableitung der Funktion F(x,y) nach x im Punkte
![P[0]](images_fsv3/function_sev_var33.gif) und schreibt
und schreibt
![limit((F(x,y[0])-F(x[0],y[0]))/(x-x[0]),P = P[0])](images_fsv3/function_sev_var34.gif) =
=
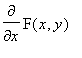 |
|
![P = P[0]](images_fsv3/function_sev_var36.gif) .
.
Graphisch lässt sich dies im Falle einer zweiwertigen Funktion sehr schön an einer Oberfläche F(x,y) im R³, entlang einer Grid-Linie, z.B. F(
![x[0], y](images_fsv3/function_sev_var37.gif) ) und der anliegenden Tangente darstellen.
) und der anliegenden Tangente darstellen.
| > |
f:=(x,y)->-(x^(1/2)*y^3);
|
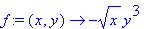
| > |
A:=plot3d(f(x,y),x=2..3,y=0..3,title=`Oberfläche mit Grid-Linie und Tangente`):
|
| > |
B:=spacecurve([a,t,f(a,t)],t=0..3,colour='blue',thickness=3):
|
| > |
f1:=unapply(diff(f(x,y),y),(x,y));
|
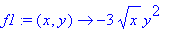
| > |
C:=spacecurve([a,t,f1(a,2)*(t-2)+f(a,2)],t=0..3,colour='red',thickness=3):
|
| > |
display3d(A,B,C,axes=FRAME);
|
Man sieht hier die Oberfläche im Raum mit der blauen Grid-Linie und der Tangente an die Linie im Punkte (
![x[0], y[0]](images_fsv3/function_sev_var310.gif) ) Die partielle Ableitung in diesem Falle nach y im Punkte ist dann der Anstieg der Tangente an diese Grid-Linie.
) Die partielle Ableitung in diesem Falle nach y im Punkte ist dann der Anstieg der Tangente an diese Grid-Linie.
![[Maple Plot]](images_fsv3/function_sev_var311.gif)
Man kann die partiellen Ableitungen von f(x,y) nach allen Variablen bilden.
| > |
f_nach_x:=diff(f(x,y), x);
|
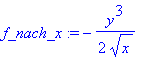
| > |
f_nach_y:=diff(f(x,y), y);
|
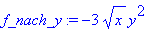
Man sieht, das Differenzieren erfolgt rein technisch nach der Regel, das nur eine der unabhängigen Variablen als veränderlich gesetzt wird, nach ihr wird differenziert, die anderen Variablen werden in diesem Fall als Konstanten angesehen.
Aufgabe:
Leiten Sie folgende Funktion partiell nach x, bzw. y ab:
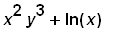
2. Partielle Ableitungen höherer Ordnung
Als Ergebnis der partiellen Ableitung erhalten wir in der Regel wiederum Funktionen von mehreren Variablen, die man wiederum ableiten kann. Man definiert also die n-te partielle Ableitung einer Funktion als die partielle Ableitung der (n-1)-ten Ableitung.
Es treten nun auch sogenannte gemischte Ableitungen auf, bei denen einmal nach x, dann nach y abgeleitet, bzw. in der anderen Reihenfolge, z.B.:
| > |
g:=(x,y)->x^2*y^3+y*ln(x);
|
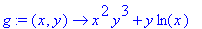
| > |
diff(g(x,y),x);# 1.partielle Ableitung nach x
|
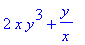
| > |
diff(g(x,y),x$2); # 2. partielle Ableitung nach x
|
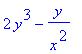
| > |
diff(g(x,y),y); # 1. partielle Ableitung nach y
|
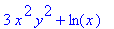
| > |
diff(g(x,y),y$2); # 2. partielle Ableitung nach y
|
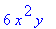
| > |
diff(diff(g(x,y),x),y); # 2. partielle Ableitung zuerst nach x und dann nach y
|
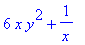
| > |
diff(diff(g(x,y),y),x); # 2. partielle Ableitung zuerst nach y und danach nach x
|
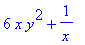
Die Frage ist, ob die partiellen gemischten Ableitungen immer unabhängig von der Reihenfolge der Variablen, nach denen abgeleitet wird.
d.h. ob
![f[xy] = f[yx]](images_fsv3/function_sev_var322.gif) immer gilt ?
immer gilt ?
Betrachen wir folgende Funktion:
| > |
g:=(x,y)->piecewise(x<>0 and y<>0,x*y*(x^2-y^2)/(x^2+y^2),otherwise,0);
|
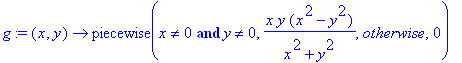
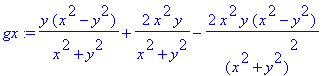
| > |
gx := y*(x^4-y^4+4*x^2*y^2)/((x^2+y^2)^2);
|
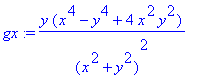
| > |
gx:=(x,y)->y*(x^4-y^4+4*x^2*y^2)/((x^2+y^2)^2);
|
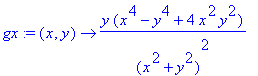
Dies ist die erste Ableitung von g nach x. Man beachte aber, dass
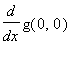 =0. Bilden wir nun die 1.partielle Ableitung nach y
=0. Bilden wir nun die 1.partielle Ableitung nach y
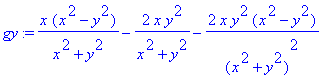
| > |
gy := x*(x^4-y^4-4*x^2*y^2)/((x^2+y^2)^2);
|
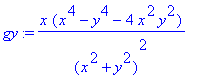
| > |
gy:=(x,y)->x*(x^4-y^4-4*x^2*y^2)/(
(x^2+y^2)^2);
|
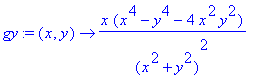
Die erste Ableitung von g nach y, aber auch hier gilt
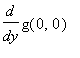 =0
=0
Somit ist die Ableitung
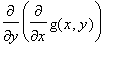 im Punkte (0,0) nach Definition
im Punkte (0,0) nach Definition
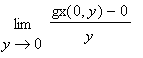
| > |
limit((gx(0,y)-0)/y, y=0);
|
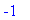
Aber die Ableitung
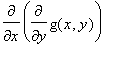 hat den Wert
hat den Wert
| > |
limit((gy(x,0)-0)/x,x=0);
|
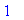
Man sieht also, dass die partiellen Ableitungen nicht immer vertauschbar sind.
Theorem (von Schwarz):
Für jede
zweimal partiell stetig ableitbare
Funktion f(x,y) gilt
![diff(diff(f,x[j]),x[i])](images_fsv3/function_sev_var337.gif) =
=
![diff(diff(f,x[i]),x[j])](images_fsv3/function_sev_var338.gif)
![]() ) und bilden den Grenzwert
) und bilden den Grenzwert
![limit((F(x,y[0])-F(x[0],y[0]))/(x-x[0]),P = P[0])](images_fsv3/function_sev_var32.gif) . Wenn dieser Grenzwert existiert, nennt man ihn die partielle Ableitung der Funktion F(x,y) nach x im Punkte
. Wenn dieser Grenzwert existiert, nennt man ihn die partielle Ableitung der Funktion F(x,y) nach x im Punkte
![]() und schreibt
und schreibt
![limit((F(x,y[0])-F(x[0],y[0]))/(x-x[0]),P = P[0])](images_fsv3/function_sev_var34.gif) =
=
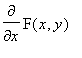 |
|
![]() .
.
![]() ) und der anliegenden Tangente darstellen.
) und der anliegenden Tangente darstellen.
![]()
![]()
![]() ) Die partielle Ableitung in diesem Falle nach y im Punkte ist dann der Anstieg der Tangente an diese Grid-Linie.
) Die partielle Ableitung in diesem Falle nach y im Punkte ist dann der Anstieg der Tangente an diese Grid-Linie.
![[Maple Plot]](images_fsv3/function_sev_var311.gif)
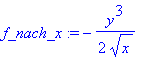
![]()
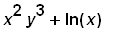
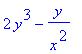
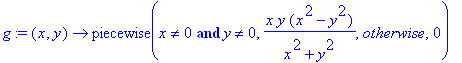
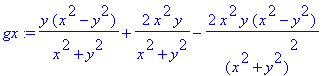
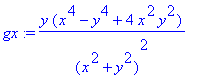
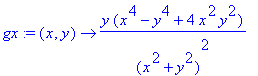
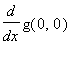 =0. Bilden wir nun die 1.partielle Ableitung nach y
=0. Bilden wir nun die 1.partielle Ableitung nach y
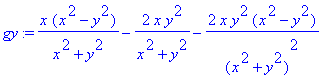
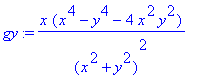
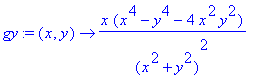
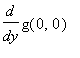 =0
=0
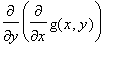 im Punkte (0,0) nach Definition
im Punkte (0,0) nach Definition
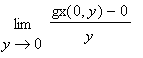
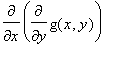 hat den Wert
hat den Wert
![diff(diff(f,x[j]),x[i])](images_fsv3/function_sev_var337.gif) =
=
![diff(diff(f,x[i]),x[j])](images_fsv3/function_sev_var338.gif)
![matrix([[diff(f,x[1])], [diff(f,x[2])], [%?], [diff(f,x[n])]])](images_fsv3/function_sev_var342.gif)