
Quelle: http://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Roulette-Tisch.jpg/640px-Roulette-Tisch.jpg
Roulette
Geschichte
Das Roulettespiel ist seit ca. 300 Jahren bekannt. Im späten 18. Jahrhundert war es vor allem in Italien (wo es seinen Ursprung haben soll) und Frankreich verbreitet, Anfang des 19. Jahrhunderts dann auch in Deutschland.
Ursprünglich war Roulette nicht als Glücksspiel, sondern als Instrument der Wahrscheinlichkeitsrechnung konzipiert. Im Laufe der Zeit wurde in Europa die Doppelnull abgeschafft, in Amerika ist sie heute noch gang und gäbe.
Das ist deshalb wichtig, weil die Regeln rund um die "Grüne Null" den Hausvorteil
entscheidend
beeinflussen.
Regeln
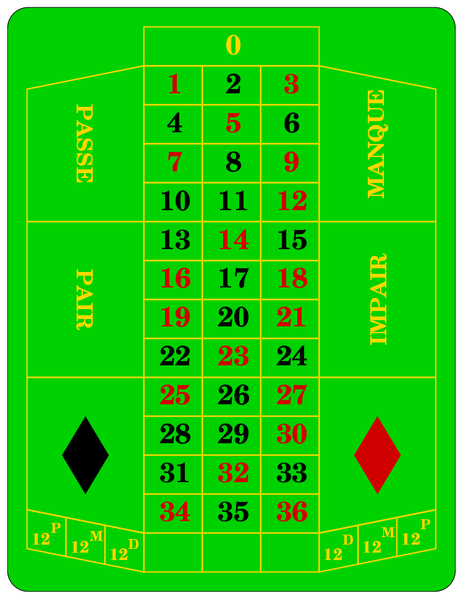
Ein typischer Roulettetisch besteht aus einem Roulettekessel und einem Tableau, an dem die Wetteinsätze getätigt werden.

Quelle: http://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Roulette-Tisch.jpg/640px-Roulette-Tisch.jpg
Ziel des Spieles ist es, in jedem einzelnen Spiel (Coup) zu erraten, auf welche Zahl die Kugel fallen wird. Dies wird durch Setzen von Jetons auf das Tableau (siehe Abbildung unten) erreicht.
Danach ermittelt der Croupier
mittels Werfen der Kugel eine Zahl, sammelt die verlierenden Einsätze ein und zahlt die glücklichen Gewinner aus.
Quelle: http://de.wikipedia.org/w/index.php?title=Datei:Roulette_frz.png&filetimestamp=20050813071117
Es gibt Dutzende Möglichkeiten, seine Jetons am Tableau zu verteilen. Für uns reichen wenige Optionen: Am beliebtesten sind die einfachen Chancen (z.B. impair/ungerade - pair/gerade,
manque/1-18 - passe/19-36, rot/schwarz). Daneben besteht noch die Möglichkeit, auf Drittel zu setzen (12P...1.Drittel usw.), auf 12 Zahlen, 9 Zahlen usw. bis auf eine einzelne Nummer.
Die Auszahlungsquoten werden so berechnet, als ob es nur 36 Zahlen gäbe, d.h. bei einfachen Chancen verdoppelt man im Falle eines Gewinns seinen Einsatz (entspricht einer Auszahlungs-
quote von 1:1). Das geht dann bis zu einzelnen Zahlen, bei denen man das 35-fache seines Einsatzes (+ die ursprüngliche Wette) erhält.
Aufgabe: Schau ob du das Prinzip dieser Wahrscheinlichkeiten verstanden hast und absolviere diesen Test!
Der Hausvorteil resultiert nun aus der "Grünen Null", dem Albtraum jedes Roulettespielers. Fällt die Kugel auf "Zéro", dann
- gewinnen die Einsätze auf die Null bzw. diejenigen, welche die Null in einer Kombination enthalten
- wird die Hälfte der Einsätze der einfachen Chancen (schwarz-rot usw.) eingezogen (alternativ: die Einsätze gehen in "Prison" und können beim nächsten Wurf freigespielt werden, gewinnen dann
aber nichts)
- verlieren alle anderen mehrfachen Chancen
Durch diese Regel sichert sich das Haus einen Bankvorteil von 1/37 x 1/2 = 1.35% bei einfachen Chancen und 1/37 = 2.70% bei allen anderen Setzvarianten. Außerdem wird beim Treffen einer
vollen Nummer erwartet, eine Spieleinheit/einen Jeton Trinkgeld zu geben (was den Hausvorteil in diesem Fall auf 5.40% anwachsen lässt). Durch zusätzliche psychologische Tricks (z.B. durch den
Einsatz von Jetons wird die dahinter stehende Geldmenge ausgeblendet, der direkt erhaltene Gewinn lässt Glückshormone ausstoßen) wird sichergestellt, dass der Spieler diesen Hausvorteil
unterschätzt oder ignoriert.
Unfehlbare Spielsysteme
Genauso alt wie das Roulettespiel selbst ist die Suche nach einem unfehlbaren System für dieses Glücksspiel. Nur wird dabei übersehen, dass der Erwartungswert (bis auf die unterschiedliche
Quote beim Setzen auf einfache/mehrfache Chancen) sich nicht beeinflussen lässt. Mit anderen Worten: Ob nun dein Mathematiklehrer oder ein blinder Orang-Utan die Jetons auf dem
Tableau verteilt, ist egal. Es gibt einfach kein mathematisches System, mit dem sich der Erwartungswert ins Positive drehen lässt. Wir werden exemplarisch den berühmtesten Versuch, die
Martingale-Strategie, enttarnen.
Ergänzung: Sehr wohl gibt es physikalische Systeme, welche die Unvollkommenheiten des Zufallsmechanismus gewinnbringend auszunutzen versuchen. So probiert man etwa, Unregelmäßigkeiten
des Wurfkessels zu entdecken, Wurfweitenspieler glauben daran, dass der Croupier beim Wurf das Ergebnis beeinflussen kann. Gerüchten zufolge gibt es weltweit etwa zehn Kesselgucker, die
aus der exakten Geschwindigkeit der Kugel und des Drehkreuzes ungefähr abschätzen können, wo die Kugel landen wird.
Zurück zu Martingale: bei dieser Strategie wird auf einfache Chancen gespielt, und im Falle des Verlustes wird der Einsatz verdoppelt. Sobald er wieder gewinnt, darf er sich über einen Gesamtgewinn
von einer Einheit freuen.
Definition: "Ein Spiel": Bei einem Spiel setzt der Martingale-Spieler solange, bis er irgendwann gewinnt und mit seinem Ausgangsbetrag neu anfängt.
Das Problem bei dieser Strategie ist, dass einerseits das Spielkapital des Spielers nicht unbegrenzt ist (das des Kasinos im Verhältnis zum Spieler dagegen schon), und es andererseits
ein sogenanntes Tischlimit gibt, d.h. die Einsätze sind "gecappt". Bei einfachen Chancen beträgt dieses im Allgemeinen 20 480,-- EUR.
Das bedeutet also, dass der Spieler bei einem Starteinsatz von 10 EUR nur 11x imstande ist, zu verdoppeln (10x2<sup>11</sup> = 20480). Das heißt weiters, dass die Wahrscheinlichkeit, eine
einzelne Serie mit Gewinn zu beenden, relativ hoch ist, nämlich
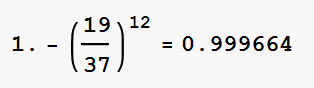
(19/37) ist dabei die Chance, bei einem Coup zu verlieren (z.B. beim Setzen auf Rot: es gewinnen 18 rote Zahlen, es verlieren 18 schwarze Zahlen und die Null). Außerdem haben wir den
"Prison"-Effekt der
Null vorerst vernachlässigt.
Man übersieht leicht, dass im Falle eines Gewinns dieser gerade 10,-- EUR beträgt, im Falle eines Verlustes jedoch 40 950,--EUR
(=10+20+40+...+20480 = 10x2<sup>12</sup>-10).
Nun können wir also leicht den Erwartungswert unseres Spiels ausrechnen: mit der hohen Wahrscheinlichkeit von oben gewinnen wir 10,--EUR,
mit einer klitzekleinen Wahrscheinlichkeit verlieren
wir 40 950,-- EUR.

D.h. unser Erwartungswert pro Spiel beträgt -3.77 EUR, das entspricht 37.7% unseres Anfangseinsatzes. Rechnen wir den "Prison"-Effekt mit hinein, beträgt die Wahrscheinlichkeit für einen Totalverlust pro Spiel
0.0287%,
der Erwartungswert beträgt dann nur mehr -1.75 EUR.
Aufgabe: Gehe das Problem von einer anderen Seite her an. Um einen Totalverlust auszugleichen, müsstest du 4095 Spiele gewinnen.
Wie hoch ist die Wahrscheinlichkeit, 4095 mal in Folge ohne Totalverlust zu gewinnen?
Andere Spielsysteme funktionieren genauso (nicht), sie haben alle eines gemeinsam: der Erwartungswert kann nicht beeinflusst werden! Auch das Beobachten der getroffenen Zahlen ("hot numbers", "cold numbers") ist
irrelevant, denn der Roulettetisch besitzt kein Gedächtnis, die Wahrscheinlichkeiten für jeden Coup sind immer gleich, egal was vorher passiert ist.
Nun solltest du auch das Grundwissen haben, um nie mehr irgendwelchen Betrügern
im Internet aufzusitzen, die ein perfektes Roulette-Spielsystem versprechen. Die Masche ist immer die gleiche: auf schlecht übersetzten
Seiten wird irgendein Spielsystem angepriesen (meist ohnehin Martingale). Dann wird
auf verschiedene Online-Casinos verlinkt - der Inhaber der Website erhält Geld von diesen Betreibern für jede Person, die sich über
diese Links anmeldet. Mit einem Hinweis á la "wechseln Sie alle 20 Minuten die Seite, sonst
stellt sich die Software auf ihr Spielverhalten ein" soll sichergestellt werden, dass sich das Opfer auf mehreren Seiten gleichzeitig
anmeldet (und einzahlt). Somit ist auch der Profit für den Webseitenbetreiber größer. Zumeist
sind diese dann auch noch frech genug, um eine Spende für ihr tolles System zu bitten.
Aufgabe: Hier findest du eine dieser typischen Webseiten. Lies sie dir aufmerksam durch und notiere dir mathematische und sonstige
Unsinnigkeiten, die dir dabei auffallen. Mit welchen psychologischen Tricks wird gearbeitet?
In der nächsten Stunde werden wir darüber ein wenig diskutieren.