| | |
| | | |
| |
| | |
| Gleichungen und Ungleichungen |
| | | |
| |
| | |
Wie war das nochmal mit den Gleichungen? Eine Gleichung ist die Behauptung, dass zwei Terme, die eine
(oder mehrere) Variable enthalten, gleich sind. Hier ein ganz einfaches Beispiel:
Wird irgendein Zahlenwert für x
eingesetzt, so entsteht in der Regel eine falsche Aussage. Falls sich aber für einen bestimmten
Zahlenwert eine wahre Aussage ergibt, so nennen wir diesen Zahlenwert eine Lösung der Gleichung.
Die Menge aller Lösungen heißt Lösungsmenge.
In den einfachsten Fällen, wie etwa im Fall der Gleichung (1), kann die
Lösungsmenge ohne großen Aufwand durch ein bisschen Nachdenken gefunden werden:
Wenn 2x um
3 vermehrt die Zahl
7 ergeben soll, so muss offenbar
2x gleich
4 sein. Da aber nun das Doppelte des gesuchten
Werts von x gleich
4 ist, ist
x gleich der Hälfte von
4, womit die (einzige) Lösung
gefunden wurde:
x = 2. Die
Lösungsmenge können wir in der Form
L = {2} anschreiben. Sie
besitzt nur ein einziges Element. Anhand derart einfacher Gleichungen können wir uns ein
grundsätzliches Bild davon machen, was eine Gleichung ist und was es bedeutet, die
Lösungsmenge zu finden.
| | | |
Gleichungen
| |
| | |
Um kompliziertere Gleichungen wie etwa
zu lösen, steht eine Reihe von Methoden zur Verfügung, von denen
einige im Gleichungskapitel besprochen wurden. Die wichtigsten bestehen darin, mit der linken und
der rechten Seite einer Gleichung das Gleiche zu machen, um damit eine andere Gleichung zu finden,
die die gleiche Lösungsmenge wie die ursprüngliche Gleichung besitzt (d.h. zu ihr äquivalent ist),
aber eine einfachere Form hat. Wer mit diesen Methoden ein bisschen Routine hat,
kann sie entweder zielgerichtet anwenden oder zumindest einige Möglichkeiten durchprobieren, um ans Ziel zu gelangen.
Aufgrund der festen Regeln, wie derartige Äquivalenzumformungen durchgeführt werden
können, hat ein Gleichungsproblem dann weniger den Charakter einer Denksportaufgabe, sondern einigermaßen
kann systematisch angegangen werden. Ein möglicher Lösungsweg für Gleichung (2)
ist dieser:
|
2x + 4 = 19 – 3x |
|
|
+
3x |
zu
beiden Seiten 3x
addieren |
|
5x + 4 = 19 |
|
|
–
4 |
von
beiden Seiten 4
subtrahieren |
|
5x = 15 |
|
|
:
5 |
beide
Seiten durch 5
dividieren |
|
x = 3 |
|
|
das
ist die (einzige) Lösung! |
|
(3a) |
|
| (3b) |
| (3c) |
| (3d) |
Beachten Sie, dass alle Gleichungen, die hier auftreten, von (3a) bis (3d),
zu (2) äquivalent sind. Erfüllt ein Wert für
x eine von ihnen, so
erfüllt er auch alle anderen! Ausgehend von Gleichung (3d), die uns ja direkt die Lösung
sagt, können Sie alle durchgeführten Umformungsschritte umkehren, um wieder zu (2) zu
gelangen. Wollen Sie die Probe machen, um sicherzugehen, dass sich kein Fehler eingeschlichen hat, so setzen Sie
einfach x = 3
in (2) ein und erhalten
2·3 + 4 = 19 – 3·3,
was sich auf die (wahre) Aussage
10 = 10
reduziert. Die Lösungsmenge von (2) ist
L = {3}.
| | | |
| |
| | |
Mit Ungleichungen, die wir in diesem Kapitel behandeln wollen, verhält es sich in mancher Hinsicht
genauso wie mit Gleichungen. (Wenn Sie nicht sicher sind, sich an das
Gleichungslösen und an die Bedeutung des Begriffs Äquivalenzumformung
richtig zu erinnern, lesen Sie dies bitte im Gleichungskapitel nach!)
Insbesondere die grundsätzliche Logik ist die gleiche:
- Eine Ungleichung ist eine Behauptung, die von einer (oder mehreren) Variablen abhängt. Allerdings behauptet
sie nicht, dass zwei Terme gleich sind, sondern dass ein Term größer oder
kleiner (oder größer-gleich oder kleiner-gleich) als ein anderer Term ist.
Beispiel:
- Variablenwerte, die eine Ungleichung erfüllen (d.h. die zu einer wahren Aussage führen, wenn sie
in die Ungleichung eingesetzt werden), stellen Lösungen dar.
- Die Menge aller Lösungen heißt Lösungsmenge.
- Einfache Ungleichungen können ohne großartigen Formalismus durch ein bisschen Nachdenken
(nach Art einer Denksportaufgabe) gelöst werden. Beispiel:
- Schaffen Sie das im Fall der Ungleichung (4)?
(Die richtige Antwort lautet: Die Lösungsmenge besteht
aus allen Zahlen x, die
größer als 2 sind!)
- Es gibt Verfahren (Äquivalenzumformungen), die gewissen Regeln genügen und
– systematisch angewandt – uns beim Auffinden der Lösungsmenge helfen.
- Um sicher zu gehen, kann für einzelne "Lösungskandidaten" immer
die Probe durch Einsetzen gemacht werden. Führt sie auf eine
wahre Aussage, so handelt es sich tatsächlich um eine Lösung.
Beispiele:
- Überprüfen Sie, dass
x = 5 eine
Lösung von (4) ist!
- Überprüfen Sie, dass
x = 3 eine
Lösung von (4) ist!
- Zeigen Sie, dass
x = 0 keine
Lösung von (4) ist!
- Ist
x = 2 eine
Lösung von (4)?
- Ist
x = 1 eine
Lösung von (4)?
Durch diese vier einfachen Übungen sollten Sie schon ein erstes Gefühl für Ungleichungen
bekommen.
| | | |
Äquivalenz-
umformungen
bei Gleichungen
| |
| | |
Allerdings gibt es auch wichtige Unterschiede zwischen Gleichungen und Ungleichungen:
- Eine Ungleichung besitzt – wie auch das einfache Beispiel (4) zeigt – in der Regel nicht nur eine, sondern viele (unendlich viele!) Lösungen.
Um die Menge all dieser Lösungen angeben (also anschreiben, verbal ausdrücken oder in irgendeiner Form grafisch darstellen)
zu können, sind etwas mehr mathematische Kenntnisse nötig als beim Hinschreiben einer einzigen Zahl.
- Die Regeln zum Umformen von Ungleichungen (Äquivalenzumformungen) sind etwas komplizierter als die Regeln
zum Umformen von Gleichungen. Manchmal führen sie auf Fallunterscheidungen.
Um die Lösungsmenge einer Ungleichung zu finden, sind dann mehrere vereinfachte
Ungleichungen zu lösen und deren Lösungsmengen zu kombinieren.
- Ungleichungsprobleme werden manchmal von vornherein in Form mehrerer Ungleichungen gestellt, die
alle gleichzeitig erfüllt sein sollen (oder – was auch vorkommt – von denen
zumindest eine erfüllt sein soll). In solchen Fällen handelt es sich genau genommen
um Ungleichungssysteme, aber diese lassen sich von den Ungleichungen weniger scharf trennen
als Gleichungssysteme von Gleichungen.
Auch wenn eine einzige Ungleichung gegeben ist, kann eine Fallunterscheidung dazu führen, dass mehrere
Ungleichungen betrachtet werden müssen. All das macht die Sache etwas komplizierter als das
Gleichungslösen.
Auch wenn wir bisher nicht sehr tief in die Materie eingedrungen sind, sollten Sie jetzt eine Idee davon haben,
was eine Ungleichung und was eine Lösung einer Ungleichung ist.
Schreiben wir eine ganz komplizierte Ungleichung hin:
x2
– 2x + 7
5 + (1 + x2)4 |
< 3x
+ 4. |
|
(5) |
Wir werden hier nicht lernen, solche Ungetüme durch Umformungen zu lösen. Aber immerhin sollten Sie jetzt
in der Lage sein, zu überprüfen, dass
x = 0
und
x = 1
Lösungen sind, aber dass
x = –2
keine Lösung ist! Versuchen Sie es!
(Und ob Sie es glauben oder nicht: In einem späteren Abschnitt dieses Kapitels
werden wir zeigen, dass es ganz einfach ist, diese Ungleichung zumindest näherungsweise
zu lösen!)
|
| | |
Logik von
Fallunterscheidungen
Gleichungssysteme
| |
| | |
| Einfache Umformungen von Ungleichungen |
| | | |
Zum Seitenanfang | |
| | |
Sehen wir uns also einige Regeln an, mit deren Hilfe Ungleichungen umgeformt werden können.
Unter "einfachen" Umformungen wollen wir solche verstehen, die eine Ungleichung in eine andere
Ungleichung überführen. Dabei sollen wir nur solche Umformungen zulassen,
die zu einer äquivalenten Ungleichung führt, also zu einer, die die gleiche
Lösungsmenge besitzt.Wie im Fall der Gleichungen nennen wir sie
Äquivalenzumformungen.
Als Grundmenge, aus die Variablenwerte stammen dürfen, wollen wir die Menge
der reellen Zahlen vereinbaren.
| | | |
reelle Zahlen
| |
| | |
Addition eines Terms zu beiden Seiten einer Ungleichung
Gehen wir aus von einer Ungleichung der Form
Dabei sind A und
B Terme, die von
einer Variablen
x abhängen können.
Die Addition eines beliebigen weiteren Terms C
zu beiden Seiten dieser Ungleichung führt auf die Ungleichung
| | | |
Terme
| |
| | |
Falls nun für einen bestimmten Wert von x
eine dieser beiden Ungleichungen erfüllt ist, ist automatisch auch die andere erfüllt.
Dabei ist es wichtig, zu bedenken, dass für einen konkreten Zahlenwert von
x auch die Terme
A,
B und
C zu Zahlen werden.
Und für Zahlen sind (6) und (7) klarerweise
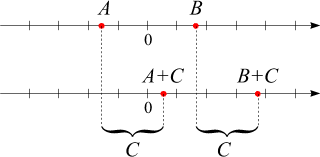
äquivalent: Dass A < B
ist, bedeutet auf der Zahlengeraden, dass
A
links von B
liegt. Eine Addition von C
entspricht einer Verschiebung auf der Zahlengeraden (nach rechts, wenn
C positiv ist und
nach links, wenn C
negativ ist). Unter einer gleichzeitigen Verschiebung von
A
und
B
bleibt, wie die nebenstehende Skizze zeigt, die Beziehung "liegt links von" aufrecht.
Da wir durch Addition von –C
zu beiden Seiten von (7) zu (6) zurückgelangen,
ist diese Art der Umformung umkehrbar.
Völlig analoge Argumentationen lassen sich für eine Ungleichung der Form
sowie für Ungleichungen der Form
| | | |
Zahlengerade
| |
| | |
(also "A kleiner oder gleich
B", kurz:
"A kleiner-gleich
B") und
(also "A größer oder gleich
B", kurz:
"A größer-gleich
B")
durchführen.
| | | |
<, >, ≤ und ≥
| |
| | |
Wir halten fest: Wird ein Term zu beiden Seiten einer Ungleichung der Form (6),
(8a), (8b) oder (8c)
addiert, so besitzt die daraus entstehende Ungleichung dieselbe Lösungsmenge
wie die gegebene.
Ein einfacher Spezialfall besteht darin, eine Zahl zu beiden Seiten einer Ungleichung
zu addieren oder von beiden Seiten zu subtrahieren.
|
|
Sehen wir uns zwei Beispiele an, bei denen diese Regel ausreicht, um die
Lösungsmenge anzugeben:
- Beispiel 1: Um die Ungleichung
2x – 3 < x + 1
zu vereinfachen, können wir so vorgehen:
|
2x – 3 < x + 1 |
|
|
–
x |
zu
beiden Seiten –x
addieren (d.h. x
subtrahieren) |
|
x
– 3 < 1 |
|
|
+
3 |
zu
beiden Seiten 3
addieren |
|
x <
4 |
|
|
|
|
(9a) |
|
| (9b) |
| (9c) |
Die resultuierende Ungleichung (9c) ist so einfach, dass sie die Lösungsmenge direkt angibt. Sie besteht
aus allen reellen Zahlen, die kleiner als 4
sind. Wir können sie in der Form
anschreiben und lesen dies als "L ist die Menge aller (reellen Zahlen) x,
für die gilt: x < 4".
Daher sind beispielsweise die Zahlen
–1/2 und
3 Lösungen, aber die Zahlen
5 und
20/3 nicht.
Der Wert 4 liegt genau an der
Grenze zwischen den Lösungen und den Nicht-Lösungen: Er stellt selbst keine Lösung dar (denn 4
ist nicht kleiner als 4, oder anders
ausgedrückt:
4 < 4
ist eine falsche Aussage), aber jede kleinere Zahl ist Lösung, jede größere nicht.
Auf der Zahlengeraden nimmt die Lösungsmenge die Form einer Halbgeraden an, die wir grafisch so darstellen können:
| | | |
für die gilt
| |
| | |
Der Randwert 4 ist als Kreislinie
eingezeichnet, um anzudeuten, dass er nicht zu
L gehört.
Beispiel 2: Um die Ungleichung
2x – 3 ≥ x + 1
zu vereinfachen, können wir so vorgehen:
|
2x – 3 ≥ x + 1 |
|
|
–
x |
zu
beiden Seiten –x
addieren (d.h. x
subtrahieren) |
|
x
– 3 ≥ 1 |
|
|
+
3 |
zu
beiden Seiten 3
addieren |
|
x ≥
4 |
|
|
|
|
(11a) |
|
| (11b) |
| (11c) |
Die resultuierende Ungleichung (11c) ist so einfach, dass sie die Lösungsmenge direkt angibt. Sie besteht
aus allen reellen Zahlen, die größer-gleich 4
(d.h. größer als 4 oder
gleich 4) sind. Wir können sie in der Form
| | | |
| |
| | |
anschreiben und lesen dies als "L ist die Menge aller (reellen Zahlen) x,
für die gilt: x ≥ 4".
Daher sind beispielsweise die Zahlen
5 und
20/3 Lösungen, aber die Zahlen
3 und
1/2 nicht.
Der Wert 4 liegt genau an der
Grenze zwischen den Lösungen und den Nicht-Lösungen: Er stellt eine Lösung dar (denn 4
ist "größer oder gleich" 4, oder anders
ausgedrückt:
4 ≥ 4
ist eine wahre Aussage). Jede größere Zahl ist Lösung, jede kleinere nicht.
Auf der Zahlengeraden nimmt die Lösungsmenge die Form einer Halbgeraden an:
Der Randwert 4 ist als voller Kreis
eingezeichnet, um anzudeuten, dass er zu
L gehört.
| | | |
| |
| | |
Diese beiden Beispiele zeigen einen Aspekt, der bei Ungleichungen häufig auftritt: Die Lösungsmengen
sind Intervalle, d.h. zusammenhängende Teilmengen der Menge der
reellen Zahlen. Mit der Schreibweise für Intervalle, wie sie
im Kapitel über Zahlen vereinbart wurde, können wir
die Lösungsmenge (10) in der Form
L = (– ∞, 4)
und
die Lösungsmenge (12) in der Form
L = [4, ∞)
anschreiben. Eine runde Klammer drückt aus, dass der betreffende Randpunkt nicht dazugehört,
eine eckige Klammer drückt aus, dass der betreffende Randpunkt dazugehört. Da
"unendlich" keine Zahl ist, wird beim Zeichen
∞ (d.h. bei
unbeschränkten Intervallen) eine
runde Klammer geschrieben.
Wir werden weiter unten sehen, dass die Lösungsmenge einer Ungleichung auch aus mehreren Intervallen zusammengesetzt sein kann.
| | | |
Intervalle
| |
| | |
Multiplikation beider Seiten einer Ungleichung mit einem Term
Die bisher besprochene Äquivalenzumformung "Addition eines Terms zu beiden Seiten einer Ungleichung"
funktioniert wie beim Umformen von Gleichungen. Der entscheidende Unterschied zum
Gleichungslösen tritt auf, wenn wir beide Seiten einer Ungleichung mit einem Term
(oder – als Spezialfall – mit einer Zahl) multiplizieren
wollen. Um diesen Unterschied sogleich einzusehen, multiplizieren wir beide Seiten der wahren
Aussage
mit –1 und erhalten die offensichtlich
falsche Aussage
So ein Malheur ist beim Gleichungslösen nicht passiert! Sein Ursprung liegt darin, dass
das Multiplizieren mit einer negativen Zahl die Reihenfolge auf der Zahlengeraden
umkehrt:
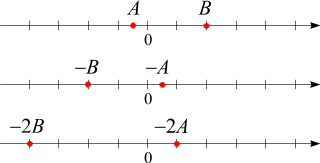
Gilt A < B (wie in der
obigen Skizze), so folgt
–A > –B
(nicht aber
–A < –B)!!
Wir können die Sache also reparieren, indem wir gleichzeitig das Kleiner-Zeichen
< durch das Größer-Zeichen
> ersetzen.
Analoges gilt für die Aussagen
A > B,
A ≤ B
und
A ≥ B.
Um aus ihnen wieder wahre Aussagen zu erhalten, können beide Seiten mit einer negativen Zahl
multipliziert werden, wenn gleichzeitig das entsprechende Ordnungszeichen (Ungleichheitszeichen) "umgedreht", also
> durch
<,
≤ durch
≥ und
≥ durch
≤ ersetzt
wird.
Werden beide Seiten einer Ungleichung mit einer positiven Zahl multipliziert, so besteht dieses Problem nicht,
und die Ordnungszeichen müssen bleiben, wie sie sind.
Beispiel: Durch Multiplikation beider Seiten der wahren Aussage (13) mit der Zahl
5 entsteht die (ebenfalls wahre)
Aussage
10 < 15.
Das Gleiche gilt, wenn wir beide Seiten einer Ungleichung mit einem Term multiplizieren, von dem sichergestellt
ist, dass er nur positive bzw. negative Werte annehmen kann. Eine solche Umformung kann rückgängig
gemacht werden, indem durch den entsprechenden Term dividiert (also mit seinem Kehrwert multipliziert)
und, falls er negativ ist, die Ordnungszeichen umgedreht und damit wieder in die
ursprüngliche Form gebracht werden.
Wir halten fest:
- Werden beide Seiten einer Ungleichung der Form (6),
(8a), (8b) oder (8c)
mit einem Term multipliziert, von dem sichergestellt ist, dass er positiv ist,
so besitzt die daraus entstehende Ungleichung dieselbe Lösungsmenge
wie die gegebene.
- Werden beide Seiten einer solchen Ungleichung
mit einem Term multipliziert, von dem sichergestellt ist, dass er negativ ist,
und werden gleichzeitig die Ordnungszeichen "umgedreht",
so besitzt die daraus entstehende Ungleichung dieselbe Lösungsmenge
wie die gegebene.
Einfache Spezialfälle bestehen darin, beide Seiten einer Ungleichung
mit einer positiven bzw. negativen Zahl zu multiplizieren oder durch eine solche
Zahl zu dividieren.
|
|
Sehen wir uns zwei einfache Beispiele an, bei denen diese Regel (zusammen mit der vorigen) ausreicht, um die
Lösungsmenge anzugeben:
- Beispiel 1: Um die Ungleichung
3x – 3 ≤ x + 1
zu vereinfachen, können wir so vorgehen:
|
3x – 3 ≤ x + 1 |
|
|
–
x |
zu
beiden Seiten –x
addieren (d.h. x
subtrahieren) |
|
2x
– 3 ≤ 1 |
|
|
+
3 |
zu
beiden Seiten 3
addieren |
|
2x ≤
4 |
|
|
:
2 |
beide
Seiten mit
1/2 multiplizieren
(d.h. durch 2
dividieren) |
|
x ≤
2 |
|
|
|
|
(15a) |
|
| (15b) |
| (15c) |
| (15d) |
Die resultuierende Ungleichung (15d) ist so einfach, dass sie die Lösungsmenge direkt angibt. Sie besteht
aus allen reellen Zahlen, die kleiner-gleich 2
sind. Wir können sie in der Form
|
L = { x | x ≤ 2 } = (– ∞, 2]
|
|
|
(16) |
anschreiben. Auf der Zahlengeraden nimmt die Lösungsmenge die Form einer Halbgeraden an:
Der Randwert 2 ist als voller Kreis
eingezeichnet, um anzudeuten, dass er zu
L gehört.
- Beispiel 2: Um die Ungleichung
1 – 5x < 13 – x
zu vereinfachen, können wir so vorgehen:
|
1 – 5x < 13 – x |
|
|
+
x |
zu
beiden Seiten x
addieren |
|
1 – 4x
< 13 |
|
|
–
1 |
von
beiden Seiten 1
subtrahieren |
|
– 4x <
12 |
|
|
:
(– 4) |
beide
Seiten mit
–1/4 multiplizieren und
< durch
> ersetzen |
|
x >
–3 |
|
|
|
|
(17a) |
|
| (17b) |
| (17c) |
| (17d) |
Die resultuierende Ungleichung (17d) ist so einfach, dass sie die Lösungsmenge direkt angibt. Sie besteht
aus allen reellen Zahlen, die größer als –3
sind. Wir können sie in der Form
|
L = { x | x > –3 } = (–3, ∞)
|
|
|
(18) |
anschreiben. Auf der Zahlengeraden nimmt die Lösungsmenge die Form einer Halbgeraden an:
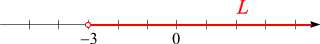
Der Randwert 3 ist als Kreislinie
eingezeichnet, um anzudeuten, dass er nicht zu
L gehört.
Wir merken noch an, dass diese Ungleichung auch auf andere Weise so gelöst werden kann:
|
1 – 5x < 13 – x |
|
|
+
5x |
zu
beiden Seiten 5x
addieren |
|
1 <
13 + 4x |
|
|
–
13 |
von
beiden Seiten 13
subtrahieren |
|
–12
< 4x |
|
|
:
4 |
beide
Seiten durch
4 dividieren |
|
–3
< x |
|
|
|
|
(19a) |
|
| (19b) |
| (19c) |
| (19d) |
Die resultuierende Ungleichung (19d) besagt, dass
–3 kleiner als
x ist, und das ist klarerweise
das Gleiche wie die Aussage, dass
x größer als
–3 ist,
was genau die Lösungsmenge (18) ergibt.
Beim letzten Schritt haben wir eine Umformung vorgenommen, wie die ebenfalls als Regel formulieren wollen:
|
Wir halten fest: Jede Ungleichung kann "in umgekehrter Reihenfolge" gelesen werden kann: Die Aussage
A < B
ist gleichbedeutend mit
B > A,
und die Aussage
A ≤ B
ist gleichbedeutend mit
B ≥ A.
|
|
Alle bisher betrachteten Ungleichungen, abgesehen vom Ungetüm (5), waren
lineare Ungleichungen, d.h. ihre linken und rechten Seiten waren alle von der Form
ax + b mit
zwei gegebenen reellen Zahlen
a und
b. Alle
Ungleichungen dieses Typs können mit Hilfe der bisher besprochenen Verfahren
gelöst werden. Manchmal (besonders in Übungsaufgaben) treten Ungleichungen
auf, die nicht diese Form haben, sich aber leicht auf lineare Ungleichungen zurückführen
lassen.
- Beispiel: Um die Ungleichung
x2 – 3 ≤ (x + 1)(x
– 2)
zu vereinfachen, können wir so vorgehen:
|
x2 – 3 ≤ (x + 1)(x
– 2) |
|
|
|
die
Klammer ausmultiplizieren |
|
x2
– 3 ≤ x2 – x
– 2 |
|
|
–
x2 |
von
beiden Seiten x2
subtrahieren |
|
–
3 ≤ – x – 2 |
|
|
|
|
(20a) |
|
| (20b) |
| (20c) |
Die resultuierende Ungleichung (20c) ist vom linearen Typ. Lösen Sie sie mit den bisher
besprochenen Methoden!
Als Lösungsmenge sollten Sie erhalten:
L = { x | x ≤ 1 } = (– ∞, 1]
.
Die interessantesten sowohl in der "reinen Mathematik" als auch in Anwendungen auftretenden Ungleichungen
sind aber nicht von diesem einfachen Typ, sondern ein bisschen (manchmal auch sehr viel)
komplizierter. In solchen Fällen kommt eine weitere Methode zum Tragen,
auf die wir im nächsten Abschnitt eingehen.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Fallunterscheidungen sind erfahrungsgemäß bei SchülerInnen und Studierenden unbeliebt.
Wird aber das ihnen zugrunde liegende Prinzip verstanden, so stellen sie zumindest keine
Hexerei dar.
| | | |
| |
| | |
Ungleichungen mit Bruchtermen
Steigen wir gleich ein und betrachten die folgende Ungleichung:
Hier sollte Ihnen zunächst auffallen, dass die linke Seite nicht definiert ist, wenn
x = 1
gesetzt wird. (Division durch 0
ist undefiniert!) Wir können also – vor jeder anderen Überlegung – die Menge,
aus der die Werte der Variablen x
grundsätzlich stammen dürfen, einschränken: Wir legen als Definitionsmenge
die Menge aller von 1
verschiedenen reellen Zahlen fest. Im Folgenden muss also
x ≠ 1
sein. Falls Sie das auch formal hinschreiben wollen (oder müssen), so notieren Sie diese
Menge einfach in einer der beiden folgenden Schreibweisen:
|
D = { x | x ≠ 1 } =
R \ { 1 }
|
. |
|
(22) |
| | | |
| |
| | |
Dabei bezeichnet R die
Menge der reellen Zahlen, und der Backslash \
drückt das Bilden der
Komplementärmenge (also das "Herausnehmen" oder "Auslassen") aus.
Nachdem das erledigt ist, stellt sich also die Frage, wie die Lösungsmenge
von (21) gefunden werden kann. Im Fall einer Gleichung (wenn in (21) anstelle
von ≥ das Gleichheitszeichen
= stünde) würden wir
beide Seiten einfach mit dem Nenner der linken Seite, also mit
x – 1,
multiplizieren. Dass dieser Term nicht
0 werden kann, ist ja durch die Einschränukung auf die
Definitionemenge (22) sichergestellt. Aber grundsätzlich kann er – je nach dem
Wert von x –
einen positiven oder einen negativen Wert annehmen. Zwischen diesen beiden Fällen
müssen wir unterscheiden – wir machen eine Fallunterscheidung:
- Wir untersuchen zuerst, ob es unter allen x,
für die x – 1 > 0 ist,
Lösungen gibt.
- Danach untersuchen wir, ob es unter allen x,
für die x – 1 < 0 ist,
Lösungen gibt.
Die Lösungen, die wir auf diese Weise finden, bilden zusammen die Lösungsmenge der gegebenen Ungleichung
(21).
- Fall x – 1 > 0:
Das bedeutet also x > 1.
Wir multiplizieren beide Seiten von (21) mit
x – 1. Da vorausgesetzt wird,
dass x – 1 > 0 ist, muss das
Ordnungszeichen nicht umgedreht werden. Wir erhalten die Ungleichung
x – 2 ≥ 3(x – 1)
und formen um:
|
x – 2 ≥ 3(x – 1) |
|
|
|
die
Klammer ausmultiplizieren |
|
x
– 2 ≥ 3x – 3 |
|
|
–
x |
von
beiden Seiten x
subtrahieren |
|
–2
≥ 2x – 3 |
|
|
+
3 |
zu
beiden Seiten 3
addieren |
| 1
≥ 2x |
|
|
: 2 |
beide
Seiten durch 2
dividieren |
| 1/2
≥ x |
|
|
|
Reihenfolge umdrehen |
| x
≤ 1/2 |
|
|
|
|
(23a) |
|
| (23b) |
| (23c) |
| (23d) |
| (23e) |
| (23f) |
Gibt es also unter allen Zahlen x, die
x > 1
erfüllen, solche, die auch
x ≤ 1/2 erfüllen?
Nein, denn diese beiden Bedingungen schließen einander aus! Keine Zahl kann größer als
1 und gleichzeitig kleiner-gleich
1/2 sein. Dieser Fall liefert also keine
Lösungen. Wir können formal
L1 = { } notieren: Fall 1
liefert keine Lösungen, was der leeren Menge entspricht.
- Fall x – 1 < 0:
Das bedeutet also x < 1.
Wir multiplizieren beide Seiten von (21) mit
x – 1. Da vorausgesetzt wird,
dass x – 1 < 0 ist, muss nun das
Ordnungszeichen umgedreht, d.h. ≥
durch ≤
ersetzt werden. Wir erhalten die Ungleichung
x – 2 ≤ 3(x – 1)
und formen um:
|
x – 2 ≤ 3(x – 1) |
|
|
|
die
Klammer ausmultiplizieren |
|
x
– 2 ≤ 3x – 3 |
|
|
–
x |
von
beiden Seiten x
subtrahieren |
|
–2
≤ 2x – 3 |
|
|
+
3 |
zu
beiden Seiten 3
addieren |
| 1
≤ 2x |
|
|
: 2 |
beide
Seiten durch 2
dividieren |
| 1/2
≤ x |
|
|
|
Reihenfolge umdrehen |
| x
≥ 1/2 |
|
|
|
|
(24a) |
|
| (24b) |
| (24c) |
| (24d) |
| (24e) |
| (24f) |
(Das ist die gleiche Rechnung wie (23a) – (23f), nur mit
umgekehrten Ordnungszeichen. Wir müssten sie also eigentlich gar nicht im Detail ausführen).
Die Frage lautet nun:
Gibt es unter allen Zahlen x, die
x < 1
erfüllen, solche, die auch
x ≥ 1/2 erfüllen?
Die Antwortet lautet Ja! Es sind dies alle Zahlen x,
die die Ungleichungskette
erfüllen, also alle Zahlen "zwischen 1/2
und 1", wobei
1/2 dazugehört,
1 aber nicht. Auf der Zahlengeraden entspricht
das einem halb-offenen Intervall. Fall 2 liefert also die Lösungen
L2 = { x | 1/2 ≤ x < 1 } = [1/2, 1).
| | | |
Komplementärmenge
| |
| | |
Die gesamte Lösungsmenge der Ungleichung (21) besteht nun aus allen in den
beiden Fällen gefundenen Lösungen, d.h. sie ist die Vereinigungsmenge der beiden
Teil-Lösungsmengen L1
und
L2:
|
L = L1 ∪
L2 =
{ x | 1/2 ≤ x < 1 } = [1/2, 1)
.
|
|
|
(26) |
Da in diesem Beispiel L1 die leere Menge ist,
stimmt L
mit L2
überein. Auf der Zahlengeraden dargestellt, sieht die Lösungsmenge so aus:
Unter dem Strich haben wir mit (25) die gegebene Ungleichung (21) auf
zwei (sehr einfache) Ungleichungen reduziert (nämlich
1/2 ≤ x
und
x < 1),
die
beide von jeder Lösung erfüllt sein müssen, denn wir können
(26) auch in der Form
|
L =
{ x | 1/2 ≤ x und x < 1 }
|
|
|
(27) |
schreiben.
Fallunterscheidungen sind eine wirksame Methode des mathematischen Argumentierens. Wichtig in diesem
Zusammenhang ist:
|
Bei einer Fallunterscheidung müssen immer alle Fälle, die auftreten können,
berücksichtigt werden!
|
|
Im obigen Beispiel sind das die Fälle
x – 1 > 0,
x – 1 < 0 und
x – 1 = 0.
Die ersten beiden Fälle haben wir berücksichtigt.
Der letzte Fall (der x = 1
bedeutet) führt nicht zu einer Lösung, da 1
nicht in der Definitionsmenge (22) enthalten ist.
Als zweites Beispiel für die Anwendung einer Fallunterscheidung betrachten wir die Ungleichung
Sie sieht ganz ähnlich aus wie (21), nur steht nun
< anstelle von
≥.
Da die einzelnen Umformungen ganz analog zu (21) funktionieren, werden wir
den Weg zu ihrer Lösung nur skizzieren. (Führen Sie die Details selbst aus!)
Wieder ist die Definitionsmenge (d.h. die Menge der für
x
grundsätzlich erlaubten Werte) durch (22) gegeben, und wieder wollen wir beide
Seiten mit
x – 1
multiplizieren. Da x – 1
positiv oder negativ sein kann, führen wir wieder eine Fallunterscheidung durch:
- Fall x – 1 > 0:
Das bedeutet also x > 1.
Wir multiplizieren beide Seiten von (28) mit
x – 1 und erhalten die
Ungleichung
x – 2 < 3(x – 1).
Diese formen wir mit Hilfe der bereits besprochenen Methoden um und erhalten schließlich
x > 1/2.
Gibt es also unter allen Zahlen x, die
x > 1
erfüllen, solche, die auch
x > 1/2 erfüllen?
Ja, die gibt es, und es sind alle Zahlen, die
x > 1 erfüllen.
Dier zweite Bedingung x > 1/2
ist dann automatisch erfüllt. (Wie haben hier ein Beispiel zweier Ungleichungen, von denen eine
stärker ist als die andere. Die schwächere kann dann ignoriert werden).
Fall 1 liefert also die Lösungen
L1 =
{ x | x > 1 } = (1, ∞).
- Fall x – 1 < 0:
Das bedeutet also x < 1.
Wir multiplizieren beide Seiten von (28) mit
x – 1. Da vorausgesetzt wird,
dass x – 1 < 0 ist, muss nun das
Ordnungszeichen umgedreht, d.h. <
durch >
ersetzt werden. Wir erhalten die Ungleichung
x – 2 > 3(x – 1)
und formen sie mit den bewährten Methoden zu
x < 1/2
um. Gibt es also unter allen Zahlen x, die
x < 1
erfüllen, solche, die auch
x < 1/2 erfüllen?
Ja, die gibt es, und es sind alle Zahlen, die
x < 1/2 erfüllen.
(In diesem Fall ist die Ungleichung
x < 1/2 die stärkere).
Fall 2 liefert also die Lösungen
L2 =
{ x | x < 1/2 } = (– ∞, 1/2).
| | | |
Vereinigungsmenge
| |
| | |
Die gesamte Lösungsmenge der Ungleichung (28) besteht aus allen in den
beiden Fällen gefundenen Lösungen, d.h. sie ist die Vereinigungsmenge der beiden
Teil-Lösungsmengen L1
und
L2:
|
L = L1 ∪
L2 =
(– ∞, 1/2) ∪ (1, ∞)
.
|
|
|
(29) |
Auf der Zahlengeraden wird sie als Vereinigungsmenge zweier Halbgeraden dargestellt:
Unter dem Strich haben wir mit (29) die gegebene Ungleichung (28) auf
zwei (sehr einfache) Ungleichungen reduziert (nämlich
x < 1/2
und
x > 1),
von denen jede Lösung (zumindest) eine erfüllen muss,
denn wir können (29) auch in der Form
|
L =
{ x | x < 1/2 oder x > 1 }
|
|
|
(30) |
schreiben.
Beachten Sie den Unterschied zwischen (27) und (30)! Verstehen Sie, warum die Lösungsmenge
im ersten Fall zusammenhängend ist und im zweiten nicht?
| | | |
| |
| | |
Betragsungleichungen
Besonders wichtig für Anwendungen innerhalb der Mathematik sind Ungleichungen, die Beträge enthalten. Erinnern wir uns: Der Absolutbetrag (kurz
Betrag) einer reellen Zahl ergibt sich, wenn "ihr Vorzeichen auf
+
gestellt wird", also etwa
| 3 | = 3
und
| –3 | = 3.
Auf der Zahlengeraden hat der Betrag einer Zahl die Bedeutung ihres
Abstands vom Nullpunkt:
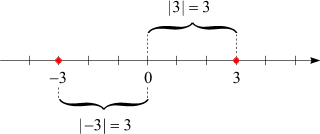
Er kann nie negativ werden, ist also immer
≥ 0.
In formaler Hinsicht kann er so festgelegt werden:
- Ist eine Zahl a entweder gleich
0 oder positiv (d.h. ist
a ≥ 0), so gilt
| a | = a.
- Ist eine Zahl a negativ
(d.h. ist a < 0), so gilt
| a | = – a.
Vielleicht erscheint Ihnen die Beziehung | a | = – a
seltsam. Aber probieren Sie es aus:
| –7 | = –(–7) = 7.
Das Minuszeichen in der Formel
| a | = – a
löscht das negative Vorzeichen von
–7
gewissermaßen aus, so dass sich im Endeffekt die positive Zahl
7 ergibt.
Besonders bedeutsam sind Terme der Form
| x – a |,
wobei a eine gegebene Zahl ist.
Auf der Zahlengeraden ist die Bedeutung eines solchen Terms der Abstand des Punktes
x vom Punkt
a:
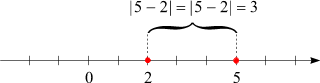
Das lässt sich mit Hilfe einer Fallunterscheidung auch formal überprüfen. Je nach den Zahlenwerten
von x
und a
können drei Fälle eintreten:
- Ist x – a > 0,
also x > a, so ist
| x – a | = x – a.
Das ist die Differenz "größere minus kleinere Zahl", also gerade der Abstand der beiden Zahlen.
- Ist x – a < 0,
also x < a, so ist
| x – a | = – (x – a)
= a – x.
Auch das ist die Differenz "größere minus kleinere Zahl" (denn jetzt ist ja
a die größere Zahl), also gerade
der Abstand der beiden Zahlen.
- Ist schließlich x – a = 0,
also x = a, so ist
| x – a | = | 0 | = 0.
Auch das ist der Abstand der beiden Zahlen (er ist 0,
weil sie gleich sind).
Die Ungleichung
besagt also: Der Abstand zwischen x
und der (gegebenen) Zahl 5 ist
kleiner als 1, unabhängig davon,
ob x auf der Zahlengeraden
links oder rechts von 5 liegt.
Die Lösungsmenge dieser Ungleichung ist daher
|
L =
{ x | 4 < x < 6 } = (4, 6)
.
|
|
|
(32) |
Auch sie kann formal mit Hilfe einer Fallunterscheidung gewonnen werden:
Der Term x – 5
kann ≥ 0 und
< 0 sein.
- Fall x – 5 ≥ 0:
Es gilt | x – 5 | = x – 5.
Die Ungleichung (31) besagt
x – 5 < 1,
daher ist
L1 = [5, 6).
- Fall x – 5 < 0:
Es gilt | x – 5 | = 5 – x.
Die Ungleichung (31) besagt
5 – x < 1,
daher ist
L2 = (4, 5).
Die gesamte Lösungsmenge von (31) ist daher
L = (4, 5) ∪ [5, 6) = (4, 6).
Auf der Zahlengeraden dargestellt, sieht sie so aus:
In dieser Form ist besonders schön zu erkennen, dass L aus
allen Zahlen besteht, die von 5 einen kleineren
Abstand als 1 besitzen.
Ungleichungen vom Typ (31) können dazu benutzt werden, um auszudrücken,
dass zwei Zahlen nahe beieinander liegen. Beispielsweise besagt die Ungleichung
| | | |
Absolutbetrag
| |
| | |
dass x ziemlich nahe bei
7 liegt: Ihr Abstand ist
kleiner als ein Tausendstel. Bedingungen dieser Art spielen beispielsweise dann eine Rolle,
wenn von einem Term ausgedrückt werden soll, dass er sich unter einer kleinen
Änderung von x nur
geringfügig ändert. (Ein solcher Term stellt dann eine "stetige Funktion" dar, wie
in einem späteren Kapitel besprochen wird).
Auch kompliziertere Betragsungleichungen wie etwa
|
| x – 3 | + | x + 3 | ≥ 8
|
|
|
(34) |
können durch (entsprechend aufwändigere) Fallunterscheidungen gelöst werden. Wenn Sie sich
die Bedeutung des Betrags auf der Zahlengeraden vor Augen halten, können Sie derartige Ungleichungen
aber unter Umständen auch einfacher lösen. So besagt etwa (34), dass die Summe
der Abstände des Punktes x
von den beiden Punkten 3
und –3 nicht kleiner als
8 ist. Liegt x
zwischen –3 und
3, so ist diese Bedingung nicht erfüllt, denn dann
ist diese Summe 6. Bewegen Sie nun
x in Ihrer Vorstellung auf der Zahlengeraden
langsam von 3 ausgehend nach rechts, so wird diese
Summe immer größer. Erreicht
x den Wert
4, so ist sie auf
8 angewachsen, wie diese Skizze zeigt:
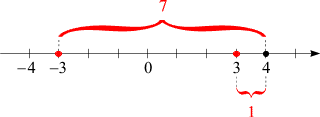
Wenn x
weiter vergrößert wird, wächst auch sie. Daher erfüllen alle
x ≥ 4 die Ungleichung (34).
Analog können Sie x auf der Zahlengeraden
von –3 ausgehend nach links bewegen, um
zu erkennen, dass auch alle x ≤ – 4 die Ungleichung (34)
erfüllen. Die gesamte Lösungsmenge ist
L = { x | x ≤ – 4 oder x ≥ 4 }
= (– ∞, – 4] ∪ [4, ∞).
|
| | |
Stetigkeit
| |
| | |
| Rückführung auf Gleichungen |
| | | |
Zum Seitenanfang | |
| | |
Ungleichungen können auf verschiedene Weise auf Gleichungen zurückgeführt werden, wodurch sich das Spektrum
an Ungleichungen, die rechnerisch ohne allzu großen Aufwand gelöst werden können, erheblich vergrößert.
| | | |
| |
| | |
Die Methode der Zwischenpunkte
Manchmal stellen die Terme auf beiden Seiten einer Ungleichung so genannte "stetige Funktionen" dar. Wir werden auf
den Stetigkeitsbegriff in einem späteren Kapitel eingehen, doch das Prinzip
ist einfach und kann uns beim Lösen von Ungleichungen helfen:
Wenn sich beide Seiten einer Ungleichung unter sehr kleinen Änderungen der Variable
x nur geringfügig
ändern, also keine "Sprünge" machen, so können wir uns vorstellen, den Wert von
x
langsam zu erhöhen und damit sozusagen alle reellen Werte zu durchlaufen.
In manchen Bereichen wird die Ungleichung erfüllt, in anderen Bereichen wird sie
verletzt sein. Der springende Punkt ist nun, dass der Übergang von einem Bereich,
in dem sie erfüllt ist, zu einem Bereich, in dem sie verletzt ist, genau dort stattfinden muss,
wo ihre beide Seiten gleich groß sind! Um diese Zwischenpunkte zu finden, muss also
die Gleichung gelöst werden, die dadurch entsteht, dass das Ungleichheitszeichen
(<, ≤, > oder ≥) durch das Gleichheitszeichen
= ersetzt wird.
In der Regel wird es nur einige wenige derartige Zwischenpunkte (also Lösungen der entsprechenden Gleichung)
geben. Die Bereiche, in denen die gegebene Ungleichung erfüllt ist (und die zusammengesetzt die Lösungsmenge ergeben),
werden dann durch diese Zwischenpunkte begrenzt, womit das Problem schon fast gelöst ist.
Wichtig ist, dass jedes Intervall, das von zwei solchen Zwischenpunkten begrenzt wird, entweder nur Lösungen oder
nur Nicht-Lösungen enthält!
Falls die Lösungsmenge der Ungleichung einzelne
– isolierte – Punkte enthält, so werden sie ebenfalls auf diese Weise gefunden.
Betrachten wir zwei Beispiele:
- Beispiel 1: Um die (lineare) Ungleichung
zu lösen, lösen wir zunächst die aus ihr entstehende Gleichung
3x + 2 = 5x – 6.
Sie besitzt nur eine einzige Lösung, nämlich
x = 4.
Diese teilt die Zahlengerade in drei Teilmengen (von denen eine nur den Zwischenpunkt enthält), die wir der Reihe nach sehr einfach darauf
überprüfen können, ob sie Lösungen oder Nicht-Lösungen enthalten:
- Zahlen kleiner als 4: Sie sind entweder alle Lösungen
oder alle keine Lösungen von (35). Machen wir eine Stichprobe:
Die Zahl 0 (sie ist kleiner als 4)
löst unsere Ungleichung
nicht, denn mit x = 0
wird (35) zur falschen Aussage
2 < – 6.
Daher sind alle Zahlen kleiner als 4
keine Lösungen von (35).
- Die Zahl 4: Da (35) mit
x = 4 auf die
falsche Aussage
14 < 14
führt, ist die Zahl 4
ebenfalls keine Lösung von (35).
- Zahlen größer als 4: Sie sind
Lösungen von (35). Wir machen die Stichprobe: Die Zahl
x = 5
(sie ist größer als 4) führt
auf die wahre Aussage
17 < 19.
Daher sind alle Zahlen größer als 4
Lösungen von (35).
Insgesamt ist die Lösungsmenge also durch
L = (4, ∞)
gegeben. (Dieses Ergebnis hätten wir natürlich auch mit der oben
besprochenen Methode der Äquivalenzumformungen erhalten können).
| | | |
Stetigkeit
| |
| | |
- Beispiel 2: Um die (quadratische) Ungleichung
zu lösen, lösen wir zunächst die aus ihr entstehende Gleichung
x2 = 5x – 6.
Wir bringen sie in die Form
x2 – 5x + 6 = 0
und finden die (einzigen) Lösungen
x1 = 2 und
x2 = 3.
Sie teilen die Zahlengerade in fünf Teilmengen, die wir der Reihe nach sehr einfach darauf
überprüfen können, ob sie Lösungen oder Nicht-Lösungen enthalten:
- Zahlen kleiner als 2: Sie sind entweder alle Lösungen
oder alle keine Lösungen von (36). Machen wir eine Stichprobe:
Die Zahl 0 löst unsere Ungleichung,
denn mit x = 0
wird (36) zur wahren Aussage
0 ≥ – 6.
Daher sind alle Zahlen kleiner als 2
Lösungen von (36).
- Die Zahl 2: Da (36) mit
x = 2 auf die
wahre Aussage
4 ≥ 4
führt, ist die Zahl 2
ebenfalls Lösung.
- Zahlen zwischen 2 und
3 (aber ohne 2 und
3 selbst): Sie sind keine Lösungen
unserer Ungleichung, wie die Stichprobe mit
x = 2.5 zeigt, denn
diese ergibt führt (36) die falsche Aussage
6.25 ≥ 6.5.
- Die Zahl 3: Da (36) mit
x = 3 auf die
wahre Aussage
9 ≥ 9
führt, löst die Zahl 3
die Ungleichung (36).
- Zahlen größer als 3: Sie sind
ebenfalls Lösungen von (36), wie die Stichprobe mit
x = 4 (sie führt
auf die wahre Aussage
16 ≥ 14)
zeigt.
Insgesamt ist die Lösungsmenge also durch
L = (– ∞, 2] ∪ [3, ∞)
gegeben. Dass die Zwischenpunkte 2 und
3 in ihr enthalten sind, resultiert natürlich daraus, dass
in (36) das Größer-gleich-Zeichen steht, also Gleichheit auch erlaubt ist.
(Ersetzen wir es durch ein Größer-Zeichen, so erhalten wir eine analoge Lösungsmenge, in der aber die
Zwischenpunkte 2 und
3 nicht enthalten sind).
Mit ein bisschen Gefühl für das Verhalten quadratischer Ausdrücke und für die Zahlengerade
können wir im Fall von (36) auch kürzer
(und eleganter) argumentieren, um das gleiche Ergebnis zu erhalten:
- Ist
x2 sehr groß (was
der Fall ist, wenn x auf der Zahlengeraden
"weit draußen" liegt, egal, ob links oder rechts), so ist unsere Ungleichung erfüllt,
da die linke Seite von (36) dann sehr viel größer ist als die rechte.
- Die beiden Zwischenpunkte
2 und
3 sind ebenfalls Lösungen, da in (36)
das Zeichen ≥
steht, das Gleichheit mit einschließt.
- Lediglich die Punkte dazwischen, also die Elemente des offenen Intervalls
(2, 3),
sind keine Lösungen, wie die Stichprobe x = 2.5
erweist.
| | | |
quadratische
Gleichungen
| |
| | |
Diese Methode kann grundsätzlich auch auf Ungleichungen angewandt werden, deren Terme sich bei manchen
Werten der Variablen Stellen sprunghaft ändern können (also unstetige Funktionen darstellen),
sofern diese Werte ebenfalls als Zwischenpunkte behandelt werden.
Beispielsweise ist die linke Seite der Ungleichung (21) ein Bruchterm,
der einen abrupten "Sprung" macht, wenn
x geringfügig
von "etwas kleiner als 1" auf
"etwas größer als 1"
erhöht wird. Bei
x = 1
(an der Sprungstelle) ist
sie, wie wir bereits bei der Besprechung dieser Ungleichung angemerkt haben, gar nicht definiert.
Die Methode der Rückführung auf eine Gleichung lässt sich aber retten, wenn
die Sprungstelle 1
als Zwischenpunkt mit berücksichtigt wird. Damit ist nur festgelegt, dass sich dort
möglicherweise eine Grenze zwischen Lösungen und Nicht-Lösungen befindet.
Das ist bei (21) auch tatsächlich der Fall:
Die Lösung der zugehörigen Gleichung
x – 2 = 3(x – 1),
die wir nach Ersetzung von ≥
durch das Gleichheitszeichen und Multiplikation beider Seiten mit
x – 1
erhalten, ist
x = 1/2, so dass
das Umschlagen von "Lösung" auf "Nicht-Lösung" (oder von "Nicht-Lösung" auf "Lösung")
nur an den Stellen 1/2
und 1 geschehen
kann. Überprüfen wir die dadurch entstandene Aufteilung der Zahlengeraden
in die Teilmengen
- x < 1/2
- x = 1/2 (Zwischenpunkt)
- 1/2 < x < 1
- x = 1 (Sprungstelle, daher ebenfalls als Zwischenpunkt behandelt)
- x > 1
so erhalten wir genau die Lösungsmenge (26). Beide Zwischenpunkte trennen
Lösungen von Nicht-Lösungen.
| | | |
stetige und unstetige
Funktionen
| |
| | |
Die Methode der Schlupfvariablen
Eine andere Methode, eine Ungleichung auf eine Gleichung zurückzuführen, ist die Methode der Schlupfvariablen.
Wir illustrieren sie anhand der Ungleichung (28), die wir bereits gelöst haben und
hier noch einmal anschreiben:
Die linke Seite muss kleiner als die rechte sein. Ist x eine
Lösung, so ist die linke Seite um einen gewissen Betrag kleiner als die rechte. Diesen Betrag kennen wir zwar nicht, aber wir bezeichnen
ihn mit s. s
steht für eine positive Zahl, d.h. es muss s > 0
sein. Wir addieren sie zur linken Seite, wodurch aus der Ungleichung eine Gleichung wird:
Diese kann nun nach x
gelöst werden. Führen Sie die Rechnung selbst durch! Sie sollten erhalten
Damit sind in gewisser Weise bereits alle Lösungen der Ungleichung (37) gefunden, denn (37) folgt
unmittelbar aus (38), sofern s > 0 ist.
Daher gibt (39) für jedes positive s
eine Lösung an! Und entsprechend der Herleitung von (39) bekommen wir auf diese Weise alle Lösungen!
Die Kunst besteht nun darin, herauszufinden, welche Werte
x annehmen kann, wenn
s alle positiven Zahlen durchläuft!
Beginnen wir mit einem großen s und lassen es langsam kleiner werden:
- Ist s sehr groß, so ist (39)
ein wenig
größer als 1. (Beispielsweise mit
s = 1000 ist
x = 999/998 ≈ 1.001).
- Lassen wir in Gedanken s kleiner werden, so wird
x langsam größer. (Beispielsweise mit
s = 100 ist
x = 99/98 ≈ 1.01).
- Mit kleiner werdendem s
wächst x unbeschränkt weiter.
Kommt s beliebig nahe an den Wert
2 heran, so wird
x beliebig groß
- Ist s = 2 erreicht, so ist
x nicht definiert.
Bisher hat x also alle Werte
größer als 1 annehmen können!
- Wird
s weiter verkleinert, so wird
x zunächst negativ, und sein Betrag ist zu Beginn sehr groß.
- Setzebn wir die Verkleinerung von
s fort, so wächst
x und wird ab
s = 1 wieder positiv (da (39)
dann den Quotienten zweier netagiver Zahlen darstellt),
- nähert sich immer mehr dem Wert 1/2
- und erreicht ihn schließlich, wenn
s = 0 ist.
(Da wir damit aber den Bereich der positiven s-Werte
verlassen haben, ist x = 1/2
keine Lösung).
Insgesamt hat
x damit alle Werte angenommen,
die kleiner als 1/2 oder größer als
1 sind – was genau der
Lösungsmenge (29) entspricht!
Der Vorteil dieser Lösungsmethode besteht darin, dass wir alle Lösungen auf
einen Schlag bekommen. Ein Nachteil besteht darin, dass sie ein gewisses Fingerspitzengefühl für die
Werte, die ein Term annehmen kann, erfordert.
Falls Sie bereits wissen, was eine Funktion ist und wie Funktionen grafisch dargestellt werden können,
werden Sie vielleicht jetzt sagen : "Man muss sich ja nur den Graphen von (39) ansehen".
Damit haben Sie vollkommen recht, und wir werden eine grafische Methode
(die sehr komfortabel ist und auch keine Schlupfvariable benötigt) als nächstes besprechen..
|
| | |
| |
| | |
| Ungleichungen grafisch lösen |
| | | |
Zum Seitenanfang | |
| | |
Manchmal versagen alle Berechnungsmethoden! Wenn sich nicht einmal die Zwischenpunkte, die die Lösungen von den Nicht-Lösungen
trennen, berechnen lassen (weil die entsprechenden Gleichungen zu kompliziert sind), kann immer noch eine Methode
angewandt werden, die die Lösungsmenge einer Ungleichung mit einem Schlag sichtbar macht! Und auch bei
einfacheren Ungleichungen liefert sie eine erste Orientierung über die Lösungsmenge
und unterstützt die Berechnung.
Wir wählen die quadratische Ungleichung (36), um diese Methode vorzustellen. Dazu bringen wir zunächst durch
eine geeignete Subtraktion die rechte Seite von (36) auf die linke, wodurch sich die (äquivalente)
Form
| | | |
| |
| | |
ergibt. Die linke Seite stellt einen Funktionsterm dar. Aber auch wenn Sie noch nicht wissen, was eine
Funktion ist, können Sie folgende Vorgangsweise einschlagen:
- Sie zeichnen ein Diagramm (mit
horizontaler x-Achse und
vertikaler y-Achse).
- In dieses Diagramm (das einen Ausschnitt der – im Prinzip unendlich ausgedehnten – Zeichenebene darstellt) tragen zu einer Auswahl von x-Werten jeweils
die Zahl, die sich aus der linken Seite von (40) durch Einsetzen des jeweiligen
x-Werts ergibt, von der
x-Achse aus in vertikale Richtung
(also als y-Wert) auf.
Dabei werden positive y-Werte nach oben und
negative y-Werte nach unten aufgetragen.
In jedem Fall ergibt sich ein Punkt in der Zeichenebene.
Ist ein y-Wert gleich
0-Wert, so liegt der entsprechende Punkt auf der
x-Achse.
Dieses Verfahren entspricht zunächst bloß dem Ausprobieren, welche der ausgewählten
x-Werte Lösungen sind und welche nicht.
Was soll daran besonders sein?
- Die Punkte der Zeichenebene, die Sie auf diese Weise erhalten, liegen alle auf einer Kurve, die
Funktionsgraph (oder kurz Graph) genannt wird. Klarerweise ist jeder x-Wert,
dessen zugehöriger
y-Wert oberhalb der
x-Achse oder auf der
x-Achse liegt, eine Lösung von
(40).
Das bedeutet:
Wenn der Graph erst einmal gezeichnet ist, erkennen Sie die Lösungsmenge mit einen Blick!
- Um den Graphen zu zeichnen, benötigen Sie aber erst einmal eine große Zahl von Punkten, sagen wir
hundert.
- Und jetzt kommt der springende Punkt: Im Zeitalter der elektronischen Hilfsmittel müssen Sie die linke Seite
von (40) nicht selbst für hundert ausgewählte
x-Werte berechnen und die zugehörigen
Punkt einzeichnen – das macht der Computer für Sie, und zwar in Form eines Funktions-Plotters!
Im Web stehen zahlreiche Funktions-Plotter oder Mathematik-Programme, die einen Funktions-Plotter integriert haben, zur Verfügung.
Sie können beispielsweise den
zur Lösung von Ungleichungen benutzen. In unserem Beispel geben Sie einfach den Term x2 – 5x + 6
in der Form
x^2-5*x+6
| | | |
Funktions-
definitionen
Zeichenebene
| |
| | |
ein. Nachdem Sie auf den Button
"Zeichnen" geklickt (oder die Enter-Taste gedrückt) haben, erscheint die gewünschte Kurve.
Der nebenstehende Screenshot zeigt einen Ausschnitt aus der Anzeige des Funktions-Plotters,
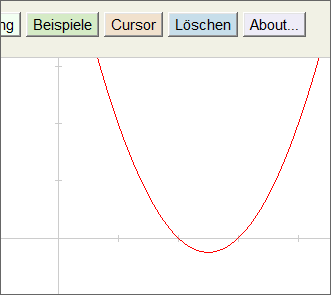wie Sie sie sehen sollten.
Aus der Lage des Graphen (der in diesem Beispiel eine Parabel ist) ist sofort ersichtlich, dass sie für
x < 2
und
x > 3
oberhalb der x-Achse liegt.
Alle diese Werte sind Lösungen von (40).
Bei x = 2
und
x = 3 schneidet die Kurve
die x-Achse. Daher sind auch
diese beiden Werte Lösungen von (40).
Nur für 2 < x < 3
liegt die Kurve unterhalb der x-Achse
– diese Werte sind keine Lösungen.
Damit haben wir damit die Lösungsmenge
L = (– ∞, 2] ∪ [3, ∞)
gefunden. Sie stimmt natürlich genau mit derjenigen überein, die wir bei der obigen Behandlung der Ungleichung in der
Form (36) gefunden haben.
Genau genommen haben wir bei diesem Beispiel Glück gehabt, da die beiden Zwischenpunkte, an denen der Graph die
x-Achse schneidet, sehr schön abzulesen sind.
Eigentlich müssten wir die x-Werte dieser Punkte
berechnen. Es sind diese jene Werte, für die die linke Seite von (40) gleich
0 ist, und das sind gerade die Lösungen jener Gleichung,
die wir erhalten, indem wir das Größer-gleich-Zeichen in (40) durch ein Gleichheitszeichen ersetzen.
Und nichts anderes haben wir zuvor bei der rechnerischen Lösung von (36) gemacht!
Sehen Sie sich den früheren Lösungsweg noch einmal an!
Unsere Methode zeigt daher die Zwischenpunkte, die die Lösungen von den Nicht-Lösungen trennt,
ebenfalls auf einen Blick. Und was besonders wichtig ist: Sie unterstützt
die Berechnung, denn sie zeigt, was berechnet werden soll: Sie lässt erkennen,
wie viele Zwischenpunkte es gibt und wo sie ungefähr liegen.
Die grafische Methode kann theoretisch für beliebige (also auch für beliebig komplizierte!) Ungleichungen angewandt werden,
solange sich ein irgendwie erkennbarer Graph ergibt. Allerdings sollte Sie dabei beachten, dass der erste Blick auf die von
einem Funktions-Plotter gezeigte Kurve täuschen kann:
- Es könnte sein, dass das Verhalten des Graphen außerhalb des angezeigten Bereichs
nicht soi ist, wie es die Darstellung nahelegt. Es könnte dann noch weitere Zwischenpunkte geben. Diese
Möglichkeit lässt sich manchmal aus der Form des eingegebenen Terms (evtl. durch eine kleine Berechnung)
ausschließen. Falls Sie sich nicht ganz sicher sind, vergrößern Sie den Bereich zur Sicherheit,
so weit es das verwendete Tool zulässt, um zumindest die Wahrscheinlichkeit zu minimieren, dass so etwas
passiert!
Beispiel: Geben Sie
x^3/8-6*x
in den ein!
Die Kurve schneidet die x-Achse in drei Punkten,
von denen aber in der Grundeinstellung nur einer im gezeigten Ausschnitt liegt! Zoomen Sie sich heraus!
- Es könnte sein, dass es im Kleinen mehr Zwischenpunkte gibt, als sie erkennen können.
Beispiel: Geben Sie
x^2-x/10
in den ein!
Die Kurve schneidet die x-Achse in zwei Punkten, die sehr nahe
beieinander liegen, von denen Sie aber in der Grundeinstellung nur einen erkennen! Zoomen Sie sich hinein!
Wir illustrieren die Methode nun noch einmal, und zwar anhand des Ungetüms (5), indem wir
diese Ungleichung zunächst in der Form
x2
– 2x + 7
5 + (1 + x2)4 |
– 3x
– 4 < 0. |
|
(41) |
anschreiben. Geben Sie nun die linke Seite dieser Ungleichung in der Form
(x^2-2*x+7)/(5+(1+x^2)^4)-3*x-4
in den ein und sehen Sie sich den Graphen an! Die Lösungen sind jetzt
aufgrund des Kleiner-Zeichens in (36) jene x-Werte,
für die der Graph unterhalb der x-Achse liegt.
Zoomen Sie sich erst heraus, um die Möglichkeit weiter draußen liegender Zwischenpunkte
möglichst auszuschließen!
Dann zoomen Sie sich an den (einzigen) Zwischenpunkt heran, um möglichst genau abzulesen, wo sich die Grenze zwischen Lösungen und Nicht-Lösungen
befindet! Die Lösungsmenge ist näherungsweise (aber immerhin mit einer sehr guten Genauigkeit) durch
|
L = { x | x > –1.25874333128112 }
|
|
|
(42) |
gegeben.
Die gleiche Methode ist auch für Betragsungleichungen anwendbar. Versuchen Sie es mit der oben besprochenen Ungleichung
(34), wobei Sie
| x – 3 |
in der Form
abs(x-3)
in den eingeben!
Enthält eine Ungleichung einen Bruchterm, dessen Nenner gleich 0
werden kann, wie etwa (28), so entfernt sich der Graph
beim betreffenden x-Wert
(der möglicherweise Lösungen von Nicht-Lösungen trennt und daher wichtig sein kann)
"ins Unendliche". In diesem Fall kann die Ablesung schwieriger sein. (Probieren Sie es mit (28) aus!).
Aber wenn Sie die grafische Methode durch die entsprechende Berechnungen unterstützen, ist sie auch in solchen Fällen
sehr hilfreich..
|
| | |
Parabel und
quadratische
Funktionen
| |
| | |
| Lineare Ungleichungen und Ungleichungssysteme in zwei Variablen |
| | | |
Zum Seitenanfang | |
| | |
Um diesen Abschnitt zu verstehen, sollten Sie ein bisschen über analytische Geometrie und vor allem über
Geradengleichungen wissen.
Er kann von kann von ''EinsteigerInnen'' ausgelassen werden.
| | | |
Analytische
Geometrie 1
| |
| | |
Lineare Ungleichungen in zwei Variablen
Bis jetzt haben wir nur Ungleichungen in einer einzigen Variablen betrachtet. Realistische Größen, von denen verlangt wird,
dass sie eine oder mehrere Ungleichungen erfüllen (wie beispielsweise die Höhe einer von mehreren Faktoren
abhängigen Investition, die einen gewissen Betrag nicht überschreiten soll), hängen in der Regel aber von mehreren
Variablen ab. Wir wollen hier den Fall zweier unabhängiger Variablen
x und
y
behandeln und uns dabei auf lineare Ungleichungen beschränken. Ein Beispiel für eine
lineare Ungleichung in zwei Variablen ist
| | | |
| |
| | |
Eine Lösung dieser Ungleichung ist ein Zahlenpaar
(x, y), das (43) zu einer wahren
Aussage macht (also "die Ungleichung erfüllt").
Während wir Werte einer Variablen grafisch als Punkte auf der Zahlengeraden darstellen konnten, müssen
wir nun die Zeichenebene verwenden, um Zahlenpaare als Punkte darzustellen. Da ein Zahlenpaar
(x, y) mit
einem Punkt der Zeichenebenebene identifiziert werden kann, kann die Lösungsmenge einer Ungleichung in zwei Variablen
als Teilmenge der Zeichenebene betrachtet werden. Um die Lösungsmenge für die Ungleichung (43) zu ermitteln,
verallgemeinern wir die oben besprochene Methode der Zwischenpunkte. Indem wir das Größer-Zeichen in
(43) in ein Gleichheitszeichen verwandeln, erhalten wir eine Gleichung in zwei Variablen, nämlich
Sie ist eine lineare Gleichung und kann daher als (implizite) Geradengleichung gedeutet werden [geom1/i.html#implGerGl].
Ihre Lösungsmenge ist daher eine Gerade, die wir
g nennen.
Mit den im ersten Kapitel über Analytische Geometrie
besprochenen Methoden (am bequemsten ist die Methode der Achsen-Abschnitte) können Sie ihre Lage in der
Zeichenebene ermitteln: Sie schneidet die
x-Achse bei
x = 3 und die
y-Achse bei
y = 2. Ihre grafische Darstellung sieht so
aus:
|
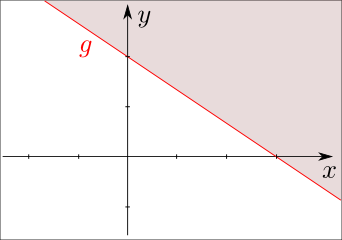
Die Gerade g verläuft schräg "von links oben nach rechts unten".
Wegen des Größer-Zeichens in (43) ist keiner ihrer Punkte eine Lösung dieser Ungleichung,
aber wir sind nahe dran: Machen wir x und
y nur ein wenig größer, so ist
(43) erfüllt.
Alle Punkte oberhalb der Geraden g erfüllen
die Ungleichung (43), alle Punkte unterhalb der Geraden
g erfüllen sie nicht. |
Die Lösungsmenge ist daher eine Halbebene, deren Begrenzungsgerade g
wegen des Größer-Zeichens in (43) nicht dazugehört, aber Lösungen von Nicht-Lösungen
trennt.
Die Lösungsmenge formal anzugeben, bringt in diesem Fall nichts Neues, denn mit der Schreibweise
|
L = { (x, y) | 2x + 3y > 6 }
|
|
|
(45) |
halten wir uns zwar noch einmal vor Augen, was die Lösungsmenge einer Ungleichung in zwei Variablen ist, aber im Wesentlichen haben
wir die Ungleichung nur abgeschrieben.
| | | |
Zahlenpaar
Zeichenebene
| |
| | |
Lineare Ungleichungssysteme in zwei Variablen
Interessant wird es, wenn mehrere lineare Ungleichungen in zwei Variablen miteinander kombiniert werden.
In praktischen Anwendungen sind oft mehrere Ungleichungen gleichzeitig zu erfüllen.
Die Formalisierung einer solchen Forderung ergibt dann ein lineares Ungleichungssystem.
Hier ein Beispiel:
Gesucht sind alle Zahlenpaare (x, y),
die beide Ungleichungen erfüllen. Als formale Form der Lösungsmenge können wir
anschreiben:
|
L = { (x, y) | 2x + 3y > 6 und
5x – 4y < 1 },
|
|
|
(47) |
was zwar nur eine Umformulierung des Ungleichungssystems (46a) – (46b) ist, uns
aber auf den richtigen Weg bringt, um eine geometrische Darstellung dieser Menge in der
Zeichenebene zu finden. Dazu ermitteln wir zuerst die Lösungsmengen
L1 und
L2
der beiden Ungleichungen (46a) und (46b). Die Lösungsmenge des
gesamten Ungleichungssystems ist dann die Durchschnittsmenge
L = L1 ∩ L2
| | | |
Durchschnitts-
menge
| |
| | |
der Lösungsmengen der einzelnen Ungleichungen. Beachten Sie, dass wir hier nicht die Vereinigung bilden,
sondern den Durchschnitt, da ja alle Ungleichungen des Systems erfüllt sein sollen:
Die Durchschnittsmenge zweier Mengen ist die Menge aller Elemente die in beiden Mengen enthalten sind. Beachten Sie
das "und" in (47) !
- Die Ungleichung (46a) haben wir bereits gelöst.
Wir nennen die Gerade, die ihre Lösungsmenge begrenzt, wieder g.
Grafisch wird
L1 in der
obigen Abbildung durch die eingefärbte Halbebene oberhalb der Geraden
g dargestellt.
- Finden Sie in analoger Weise die grafische Darstellung der Lösungsmenge L2
der Ungleichung (46b) !
- Bestimmen Sie dabei zuerst die Lage der Geraden, die die Lösungen von den Nicht-Lösungen trennt!
- Finden Sie dann heraus, welche der beiden Halbebenen, die durch die Gerade
5x – 4y = 1 voneinander
getrennt werden, die Lösungsmenge L2
darstellt! Setzen Sie beispielsweise eine beliebigen Punkt als Stichprobe ein, um das herauszufinden!
Wenn Sie alle Geraden und Mengen, die bei der Lösung dieses Problems auftreten,
in einer Skizze darstellen, so sollte sich folgendes Bild ergeben:
|
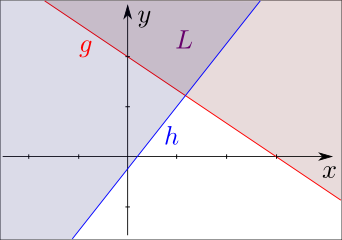
Die Menge L1 wird durch die eingefärbte Halbebene
oberhalb der Geraden g
(ohne g) dargestellt.
Die Menge L2 wird durch die eingefärbte Halbebene
oberhalb der Geraden h
(ohne h) dargestellt.
Die Lösungsmenge L des gesamten Ungleichungssystems
ist der Durchschnitt von L1 und
L2. Sie wird durch den dünkler
eingefärbten Bereich oberhalb der beiden Geraden
g und
h (ohne seinen Rand) dargestellt. |
| | | |
| |
| | |
Die Lösungsmenge L ist also der in der Skizze dargestellte Bereich oberhalb der Geraden
g und
h. Da die beiden Geraden wegen der Kleiner-Zeichen in
(46a) und (46b) nicht zu den
Einzel-Lösungsmengen gehören, gehört auch der Rand des gemeinsamen Bereichs
nicht zur Menge L. Letztere ist daher eine offene Menge.
Falls Sie die Lösungsmenge L genauer charakterisieren wollen
als durch eine Skizze, so
können Sie noch die Koordinaten des Schnittpunkts der Geraden
g und
h berechnen.
Führen Sie die Rechnung selbst durch!
Sie sollten (27/23, 28/23) ≈ (1.174, 1.217)
erhalten. Dieser Schnittpunkt ist selbst keine Lösung des Ungleichungssystems, aber er gibt an, wo die
Lösungsmenge eine "Ecke" besitzt.
Ganz analog können Sie vorgehen, um ein System mit beliebig vielen linearen Ungleichungen zu lösen. In der Regel wird die
Sache so ablaufen wie in dem soeben diskutierten Beispiel. Um keine Fehler zu machen, sollten Sie aber
bedenken:
-
Steht in einer Ungleichung ein Größer-Zeichen oder ein Kleiner-Zeichen (wie in den beiden Ungleichungen
(46a) und (46b) des obigen Beispiels),
so gehört die Gerade, die den Lösungs-Halbraum begrenzt, nicht zur Lösungsmenge dieser Ungleichung. Steht hingegen ein
Größer-gleich-Zeichen oder ein Kleiner-gleich-Zeichen in einer Ungleichung,
so gehört die Gerade, die den Lösungs-Halbraum begrenzt, zur Lösungsmenge dieser Ungleichung.
- In speziellen Fällen kann es passieren,
dass eine der auftretenden Halbebenen Teilmenge einer anderen ist und daher ignoriert werden kann.
- Es ist möglich,
dass zwei Halbebenen auftreten, deren Durchschnittsmenge leer ist. In diesem Fall besitzt das Ungleichungssystem
überhaupt keine Lösung – seine Lösungsmenge ist leer.
- Achten Sie bei einem Problem, in dem mehrer Ungleichungen auftreten, darauf, ob es wirklich so gemeint ist, dass
alle Ungleichungen erfüllt sein müssen! Es kommt auch vor, dass von mehreren Ungleichungen
zumindest eine erfüllt sein muss – dazu siehe die abschließende Bemerkung ganz unten.
| | | |
offene Menge
(in Vorbereitung)
Schnittpunkte
| |
| | |
Ungleichungssysteme können natürlich mehr als zwei Variable aufweisen. Die Lösungsmenge einer linearen
Ungleichung in drei Variablen kann als Halbraum im
R3
dargestellt werden, so dass die Lösungsmenge eines ganzen Ungleichungssystemsystems die entsprechende Durchschnittsmenge
von Halbräumen ist.
Wir erwähnen noch, dass auch nichtlineare Ungleichung und Ungleichungssysteme auf ähnliche Weise behandelt werden
können. In zwei Variablen treten an die Stelle der Geraden, die Lösungen von Nicht-Lösungen trennen,
Kurven, die manchmal mit den Mitteln der analytischen Geometrie näher bestimmt werden können.
Als Lösungsmengen von nichtlinearer Ungleichungen in zwei Variablen können (geometrisch interpretiert)
beispielsweise Kreise oder die Komplementärmengen von Kreisen auftreten. Die Lösungsmenge eines Systems
von Ungleichungen, die alle erfüllt werden müssen, ist dann
wie im linearen Fall die Durchschnittsmenge der Lösungsmengen der einzelnen Ungleichungen.
| | | |
Kurven
(in Vorbereitung)
| |
| | |
Ein anderer Typ von Ungleichungssystemen
Der Begriff "Ungleichungssystem" ist ein bisschen unscharf. Meistens ist damit gemeint, dass alle Ungleichungen eines
Systems erfüllt sein müssen. Das ist der Typ, den wir gerade besprochen haben.
Daneben gibt es auch einen anderen Typ: Es kommt vor, dass von mehreren Ungleichungen
zumindest eine erfüllt sein muss. Eine solche Situation ist beispielsweise weiter oben bei der Diskussion der
Fallunterscheidungen aufgetreten: Sehen Sie sich (29), (30) und den Text dazwischen noch
einmal an! In einem solchen Fall ist die Lösungsmenge die Vereinigung der Lösungsmengen der einzelnen Ungleichungen
und nicht ihr Durchschnitt.
Tritt eine solche Problemstellung mit linearen Ungleichungen in zwei Variablen auf, so ist ihre Lösungsmenge eine Vereinigung von Halbebenen.
Wird etwa das System (46a) – (46b) in diesem Sinn aufgefasst,
ist also die Menge aller Zahlenpaare (x, y)
gesucht, die zumindest eine der beiden Ungleichungen erfüllen, so ist die Lösungsmenge der gesamte
(in welcher Farbe auch immer)
eingefärbte Bereich in der letzten letzten der obigen Abbildungen, wobei der Rand
dieses Bereichs nicht dazugehört.
|
| | |
| |