| | |
| | | |
| |
| | |
| Dreiecke, Winkel und Winkelfunktionen |
| | | |
| |
| | |
Die Trigonometrie (genauer: ebene Trigonometrie) oder Dreiecksgeometrie ist jenes Teilgebiet der Geometrie,
das sich mit Dreiecken beschäftigt.
Sie entstand vor allem aus der frühen Astronomie, hat aber neben
der Himmelsvermessung auch zahlreiche irdische Anwendungen gefunden.
Warum ausgerechnet Dreiecke?
| | | |
| |
| | |
Dreiecke sind in der Geometrie besonders wichtig, da beliebige durch Strecken oder Geraden begrenzte ebene
Figuren in Dreiecke zerlegt werden können. In gewisser Weise bilden sie die "Atome"
in der Welt dieser Figuren. Daher können Methoden der Dreiecksgeometrie
zur Lösung einer Vielzahl komplexer geometrischer Fragestellungen angewandt werden.
Das wird unter anderem auch durch die so genannten "Vermessungsaufgaben", auf die wir weiter unten
zu sprechen kommen, illustriert.
Winkel und Winkelmaße
Wir wollen Winkel in diesem Kapitel immer im Gradmaß (Altgrad) angeben, in dem der volle Winkel 360° beträgt.
Um Teile von Graden zu bezeichnen, kann entweder die Dezimaldarstellung
oder die Unterteilung
- 1° = 60' º 60 (Winkel-)Minuten und
- 1' = 60'' º 60 (Winkel-)Sekunden
| | | |
| |
| | |
verwendet werden. (So ist beispielsweise 72.5° = 72° 30' ).
Man könnte aber genausogut das Bogenmaß verwenden,
in dem der volle Winkel 2p beträgt.
In der Landvermessung wird häufig das Neugradsystem verwendet, in dem der volle Winkel 400g (100 Neugrad oder gon)
mißt, mit der (dezimalen) Unterteilung ).
Man könnte aber genausogut das Bogenmaß verwenden,
in dem der volle Winkel 2p beträgt.
In der Landvermessung wird häufig das Neugradsystem verwendet, in dem der volle Winkel 400g (100 Neugrad oder gon)
mißt, mit der (dezimalen) Unterteilung
- 1g = 100c º 100 Neuminuten und
- 1c = 100cc º 100 Neusekunden.
Auf Taschenrechnern kann üblicherweise mit Hilfe der Taste "DRG" (für deg, rad und grad) zwischen diesen
Systemen umgeschaltet werden. Falls Sie ein Computerwerkzeug verwenden,
das Winkelfunktionen nur im Bogenmäß verarbeitet, müssen Sie entsprechende Umrechnungsfaktoren
verwenden, z.B.
Winkel im Bogenmaß = Winkel im Gradmaß × p/180°.
Die Rolle der Winkelfunktionen
| | | |

Bogenmaß
| |
| | |
Zahlreiche interessante und nützliche Beziehungen in Dreiecken, vor allem jene zwischen Winkeln und Seiten, können nicht durch
elementare Rechenoperationen ausgedrückt werden. Sie erfordern neue, für diese Zwecke maßgeschneiderte
Techniken, den Formalismus der Winkelfunktionen, den wir in einem früheren Kapitel besprochen haben.
Für das Folgende sollten Sie mit den Begriffen Sinus und Cosinus vertraut sein und sie für Berechnungen im rechtwinkeligen Dreieck anwenden können.
Auch die inversen Winkelfunktionen
Arcus Sinus und Arcus Cosinus werden an einigen Stellen eine Rolle spielen.
Wichtig im Zusammenhang mit diesen beiden ist:
| | | |

Winkelfunktionen
| |
| | |
- Liegt a zwischen 0° und 180° und ist
x º sin
 a
bekannt, so ist a entweder durch
asin a
bekannt, so ist a entweder durch
asin x
( x
( £ 90°)
oder durch
180° - asin £ 90°)
oder durch
180° - asin x
( x
( ³ 90°) gegeben. ³ 90°) gegeben.
- Liegt a zwischen 0° und 180° und ist
y º cos
 a
bekannt, so ist a durch
acos a
bekannt, so ist a durch
acos y
gegeben. y
gegeben.
Bei der Berechnung eines Winkels aus seinem Sinus muss also immer ein bisschen nachgedacht werden, ob
es sich nun um den spitzen oder den stumpfen handelt.
Das geht in der Regel aus dem konkreten Zusammenhang hervor.
|
| | |

Arcus-Funktionen
| |
| | |
| Elementare Dreieckseigenschaften |
| | | |
Zum Seitenanfang | |
| | |
In diesem Abschnitt wollen wir einige elementare Eigenschaften von Dreiecken, deren Formulierung
keine Winkelfunktionen benötigen zusammenstellen. Einige dieser Themen werden Ihnen wahrscheinlich in Ihrer bisherigen Mathematik-Ausbildung
bereits begegnet sein.
Grundbegriffe, Dreieckstypen und Bezeichnungen
| | | |
| |
| | |
Ein Dreieck ist durch drei Punkte in der Ebene, die nicht auf einer Graden liegen (die Eckpunkte) gegeben.
Die Strecken, die diese drei Punkte verbinden, bilden die Seiten des Dreiecks.
Wird eine Strecke zu einer Gerade verlängert, so wird diese oft auch als Seite(nline)
bezeichnet. Die Abstände zwischen den Eckpunkten sind die Seitenlängen, sie werden ebenfalls
kurz als Seiten bezeichnet.
Daneben spielen zwei Arten von Größen in der Trigonometrie eine besondes wichtige Rolle: Winkel und Höhen.
- Unter Winkel wird in einem Dreieck immer der Innenwinkel verstanden, kann also
nicht größer sein als 180°. Wichtig ist der folgende Satz,
der Ihnen wahrscheinlich bereits bekannt ist:
| Die Summe der Winkel (Winkelsumme) ist in jedem Dreieck 180°. |
|
(1) |
(Für einen Beweis klicken Sie auf den Button rechts).
- Die Höhe(nlinie) "auf eine Seite" ist jene Gerade, die auf diese Seite normal steht und durch den
ihr gegenüberliegenden Eckpunkt geht. Die Strecke zwischen Eckpunkt und gegenüberliegender Seite wird
ebenso wie deren Länge (d.h. der Normalabstand des Eckpunkts zur gegenüberliegenden Seite) kurz als Höhe bezeichnet.
Auf den Begriff des Höhenschnittpunkts, den Sie wahrscheinlich schon kennen, werden wir weiter unten stoßen.
| | | |
| |
| | |
Wie Sie sehen, ist der Sprachgebrauch hier ein bisschen schlampig: Die Worte "Seite" und "Höhe" können
eine Strecke, eine Gerade oder eine Länge bezeichnen. In der Regel geht aus dem Zusammenhang hervor, was gemeint ist.
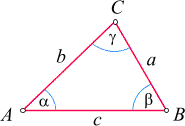 Zur Bezeichnung von Eckpunkten, Seiten, Winkeln und Höhen hat sich eine nützliche Konvention herausgebildet:
Lauten die Seitennamen a, b
und c (sie werden dann im Gegenuhrzeigersinn vergeben), so wird die
Seite c meist waagrecht (als "Grundlinie") gezeichnet.
Die Eckpunkte werden mit den entsprechenden Großbuchstaben
A, B und C
bezeichnet, wobei A der Seite a
gegenüberliegt, usw.
Die Winkel werden dann mit a, b und g
bezeichnet, wobei a der Winkel beim Punkt
A ist, usw.
Die (Länge der) Höhe auf die Seite c wird meist mit
hc bezeichnet, usw.
Zur Bezeichnung von Eckpunkten, Seiten, Winkeln und Höhen hat sich eine nützliche Konvention herausgebildet:
Lauten die Seitennamen a, b
und c (sie werden dann im Gegenuhrzeigersinn vergeben), so wird die
Seite c meist waagrecht (als "Grundlinie") gezeichnet.
Die Eckpunkte werden mit den entsprechenden Großbuchstaben
A, B und C
bezeichnet, wobei A der Seite a
gegenüberliegt, usw.
Die Winkel werden dann mit a, b und g
bezeichnet, wobei a der Winkel beim Punkt
A ist, usw.
Die (Länge der) Höhe auf die Seite c wird meist mit
hc bezeichnet, usw.
Zur Bezeichnung eines ganzen Dreiecks (z.B.
um in einer Skizze, die mehrere Dreiecke enthält, eines zu benennen), werden die
Namen der Eckpunkte aufgezählt. Man spricht dann beispielsweise vom "Dreieck ABC"
oder schreibt einfach das Kürzel DABC.
(Aber nicht verwechseln: Das Symbol D - der griechische Buchstabe "Delta" -
wird auch für andere Dinge verwendet: Manchmal bezeichnet es einen Winkel, manchmal eine Änderung!).
Zur Benennung eines Winkels in einem Dreieck können auch die drei Eckpunkte angegeben werden, und zwar
so, dass der mittlere den Scheitel des Winkels bezeichnet. So kann beispielsweise der Winkel a
des obigen Dreiecks auch als "Winkel CAB" benannt
oder, unter Verwendung des Winkel-Symbols, einfach in der Form
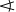 CAB geschrieben werden. CAB geschrieben werden.
Wir nennen ein Dreieck
- gleichseitig, wenn alle seine Seiten gleich lang sind (was damit gleichbedeutend ist, dass alle Winkel gleich, d.h. 60°, sind),
- gleichschenkelig, wenn es zwei gleich lange Seiten besitzt (was damit gleichbedeutend ist, dass es zwei gleiche Winkel besitzt),
- rechtwinkelig, wenn es einen rechten Winkel (90°) besitzt,
- spitzwinkelig, wenn alle seine Winkel spitz, d.h. kleiner als 90° sind und
- stumpfwinkelig, wenn es einen Winkel besitzt, der stumpf, d.h. größer als 90° ist.
Der Begriff schiefwinkelig bezeichnet an und für sich ein Dreieck, das keinen rechten Winkel besitzt,
wird aber oft für ein allgemeines Dreieck, d.h. für ein Dreieck, an das keine Bedingungen gestellt werden, verwendet.
In einem spitzwinkeligen Dreieck verläuft jede Höhe innerhalb des Dreiecks von einem Punkt bis zur
gegenüberliegenden Seite, in einem stumpfwinkeligen Dreieck hingegen gilt das nur für eine
Höhe, die beiden anderen liegen außerhalb des Dreiecks:
Der Flächeninhalt eines Dreiecks wird meist mit dem Buchstaben A bezeichnet
und ist durch die leicht zu merkende Formel
| Fläche
= |
Grundlinie
× Höhe
2 |
|
(2) |
| | | |
| |
| | |
gegeben (für einen Beweis siehe den Button rechts). Wird die Seite c als Grundlinie
gewählt, so ist
A = c hc hc / / 2.
Wir werden daraus weitere Formeln für den Flächeninhalt eines Dreiecks
gewinnen, siehe unten (7), (11) und (14). 2.
Wir werden daraus weitere Formeln für den Flächeninhalt eines Dreiecks
gewinnen, siehe unten (7), (11) und (14).
Themen aus der klassischen Geometrie
| | | |
| |
| | |
In der Trigonometrie benötigen wir einige geometrische Begriffe und Sachverhalte, die
Ihnen wahrscheinlich in Ihrer bisherigen Mathematik-Ausbildung bereits begegnet sind.
Lesen Sie im nebenstehenden Exkurs eine Zusammenfassung einiger besonders wichtiger Themen:
- Strecken und Geraden
- Wissenswertes über ebene geometrische Figuren
- Kongruenz
- Ähnlichkeit und der Strahlensatz
- Satz von Pythagoras ("Pythagoräischer Lehrsatz")
Der letzte der besprochenen Punkte, der berühmte Satz von Pythagoras, ist von besonderer Wichtigkeit,
und wir werden ihn in diesem Kapitel des Öfteren anwenden.
Zwei Erweiterungen dieses Satzes, der Katheten- und der Höhensatz, werden weiter unten besprochen.
Satz von Thales (Thaleskreis)
| | | |
Themen aus der
klassischen
Geometrie
| |
| | |
Jedes
 Dreieck, dessen Grundlinie der Durchmesser eines Kreises ist, und dessen
dritter Eckpunkt (wie in der nebenstehenden Skizze gezeigt) auf der Kreislinie liegt, ist rechtwinkelig.
Diese Aussage heißt Satz von Thales.
Generell bezeichnet man einen Winkel, dessen Scheitel auf einer Kreislinie
(altmodisch "Kreisperipherie") liegt, als Peripheriewinkel. Damit kann der
Satz auch kurz so ausgedrückt werden:
Dreieck, dessen Grundlinie der Durchmesser eines Kreises ist, und dessen
dritter Eckpunkt (wie in der nebenstehenden Skizze gezeigt) auf der Kreislinie liegt, ist rechtwinkelig.
Diese Aussage heißt Satz von Thales.
Generell bezeichnet man einen Winkel, dessen Scheitel auf einer Kreislinie
(altmodisch "Kreisperipherie") liegt, als Peripheriewinkel. Damit kann der
Satz auch kurz so ausgedrückt werden:
"Jeder Peripheriewinkel im Halbkreis ist ein rechter".
Um ihn zu beweisen, klicken Sie hier :
In der Skizze wird der Halbkreis zu einem Vollkreis und das Dreieck mit Hilfe eines zweiten
Durchmessers zu einem Viereck vervollständigt.
Letzteres ist ein Rechteck, da zwei Durchmesser eines Kreises immer ein Rechteck definieren. Damit ist der Satz bewiesen. :
In der Skizze wird der Halbkreis zu einem Vollkreis und das Dreieck mit Hilfe eines zweiten
Durchmessers zu einem Viereck vervollständigt.
Letzteres ist ein Rechteck, da zwei Durchmesser eines Kreises immer ein Rechteck definieren. Damit ist der Satz bewiesen.
Er besitzt auch eine Umkehrung: Alle Punkte, von denen aus man eine gegebene Strecke unter
einem rechten Winkel "sieht", liegen auf einer Kreislinie, für die die gegebene Strecke einen
Durchmesser bildet.
Eine Verallgemeinerung des Satzes von Thales ist der Peripheriewinkelsatz, den wir weiter unten besprechen.
Besondere Punkte und Linien im Dreieck
| | | |
| |
| | |
Vier Punkte treten sowohl in praktischen Anwendungen als auch bei der theoretischen
Erforschung der Dreieckseigenschaften immer wieder auf und werden gemeinsam als
merkwürdige Punkte bezeichnet. Für die Beweise der folgenden Aussagen
klicken Sie auf den Button rechts.
- Über Höhen und Höhenlinien haben wir bereits oben gesprochen.
In jedem Dreieck schneiden die Höhenlinien einander in einem
Punkt H, dem Höhenschnittpunkt.
- Eine Gerade, die auf eine Seitenlinie normal steht und sie halbiert, heißt
Seitensymmetrale. In jedem Dreieck schneiden die Seitensymmetralen einander
in einem Punkt U. Da dieser
Punkt von allen drei Eckpunkten gleich weit entfernt ist,
ist er der Umkreismittelpunkt, d.h. der Mittelpunkt jenes (eindeutigen)
Kreises (genannt Umkreis), auf dem alle drei Eckpunkte des Dreiecks liegen.
Der Radius R des Umkreises heißt Umkreisradius.
Wir werden weiter unten zwei Formeln für ihn angeben, siehe
(8) und (12).
- Eine Gerade, die durch einen Eckpunkt geht und den dort befindlichen Winkel halbiert,
heißt Winkelsymmetrale oder Winkelhalbierende. In jedem Dreieck schneiden die Winkelsymmetralen einander
in einem Punkt I. Dieser Punkt ist der
Inkreismittelpunkt, d.h. der Mittelpunkt jenes (eindeutig bestimmten) Kreises
(genannt Inkreis), der alle drei Seitenlinien von innen berührt.
Der Radius r des Inkreises heißt Inkreisradius.
Wir werden weiter unten zwei Formeln für ihn angeben, siehe
(13) und (15).
- Eine Gerade, die durch einen Eckpunkt und den Halbierungspunkt der gegenüberliegenden
Seite geht, heißt Schwerlinie. In jedem Dreieck schneiden die Schwerlinien einander
in einem Punkt S, dem so genannten
Schwerpunkt. Physikalisch kann er als Massenmittelpunkt
eines Systems aus drei gleich schweren Punktmassen, die an den Eckpunkten des Dreiecks sitzen,
gedeutet werden.
Warum diese vier Punkte als "merkwürdig" bezeichnet werden, liegt unter anderem an Eigenschaften
wie der folgenden, die drei von ihnen erfüllen:
- In jedem Dreieck liegen Höhenschnittpunkt, Umkreismittelpunkt und
Schwerpunkt auf einer Geraden, der so genannten Eulerschen Geraden.
Das gleichseitige Dreieck
| | | |
| |
| | |
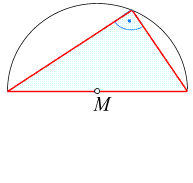
Es ist nützlich, zwei Tatsachen über das gleichseitige Dreieck zu kennen und sich zu merken.
Die erste betrifft die Länge der Höhen (die natürlich alle gleich lang sind und
einfach mit h bezeichnet werden).
 Um sie zu berechnen, betrachten wir das in der nebenstehenden
Skizze hervorgehobene (hellblaue) rechtwinkelige Dreieck und wenden entweder den Satz von Pythagoras
an oder - das ist die kürzere Argumentation - schreiben den Cosinus des eingezeichneten Winkels von 30° als
Quotient Ankathete/Hypotenuse (d.h. h/a),
benutzen die Tatsache, dass
ist und schließen daraus
Um sie zu berechnen, betrachten wir das in der nebenstehenden
Skizze hervorgehobene (hellblaue) rechtwinkelige Dreieck und wenden entweder den Satz von Pythagoras
an oder - das ist die kürzere Argumentation - schreiben den Cosinus des eingezeichneten Winkels von 30° als
Quotient Ankathete/Hypotenuse (d.h. h/a),
benutzen die Tatsache, dass
ist und schließen daraus
| | | |

spezielle Winkel
| |
| | |
Die zweite Tatsache betrifft die Lage des Höhenschnittpunkts H :
Er teilt jede Höhe im Verhältnis 2:1.
Daraus ergibt sich der Umkreisradius zu 2h :
Er teilt jede Höhe im Verhältnis 2:1.
Daraus ergibt sich der Umkreisradius zu 2h /3,
der Inkreisradius zu h /3,
der Inkreisradius zu h /3.
Die Mittelpunkte von Umkreis und Inkreis sowie der Schwerpunkt fallen aufgrund
der Symmetrie mit H zusammen. /3.
Die Mittelpunkte von Umkreis und Inkreis sowie der Schwerpunkt fallen aufgrund
der Symmetrie mit H zusammen.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir haben die Sinusfunktion ursprünglich im rechtwinkeligen Dreieck kennengelernt:
Der Sinus eines Winkels im rechtwinkeligen Dreieck ist der Quotient aus Gegenkathete und Hypotenuse.
Aber auch der Sinus eines Winkels in einem schiefwinkeligen Dreieck spielt eine nützliche Rolle.
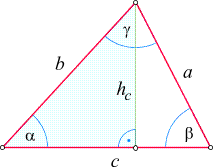 Um sie zu erschließen, betrachten wir zunächst ein spitzwinkeliges Dreieck.
Dann verläuft jede der drei Höhenlinien innerhalb des Dreiecks
von einem Punkt zur gegenüberliegenden Seite. Wir wählen, wie in der nebenstehenden Skizze, die Höhenlinie
auf die Seite c aus, um das Dreieck in zwei
rechtwinkelige Dreiecke zu zerlegen. Die Höhe hc
tritt nun
Um sie zu erschließen, betrachten wir zunächst ein spitzwinkeliges Dreieck.
Dann verläuft jede der drei Höhenlinien innerhalb des Dreiecks
von einem Punkt zur gegenüberliegenden Seite. Wir wählen, wie in der nebenstehenden Skizze, die Höhenlinie
auf die Seite c aus, um das Dreieck in zwei
rechtwinkelige Dreiecke zu zerlegen. Die Höhe hc
tritt nun
- im linken (hellblauen) rechtwinkeligen Dreieck als Gegenkathete des Winkels
a und
- im rechten (weißen) rechtwinkeligen Dreieck als Gegenkathete
des Winkels b
auf. Dies versetzt uns in die Lage, ihre Länge auf zweierlei Arten berechnen zu können:
- Im blauen
Dreieck (in dem die Seite b die Rolle der Hypotenuse spielt) erhalten wir
sin
 a = hc/b,
daher
hc = b a = hc/b,
daher
hc = b sin sin a. a.
- Im weißen Dreieck (in dem die Seite a die Rolle der Hypotenuse spielt) ergibt sich
sin
 b = hc/a,
daher
hc = a b = hc/a,
daher
hc = a sin sin b. b.
Setzen wir diese beiden Resultate für hc
gleich, so erhalten wir die Beziehung
b sin a =
a sin a =
a sin b. b. |
|
(4) |
Wir können sie beispielsweise dazu benutzen, um b zu berechnen,
wenn die Seite a und die beiden Winkel a und b
gegeben sind.
Die gleiche Argumentation kann durchgespielt werden, wenn das Dreieck durch die Höhe auf a
in zwei rechtwinkelige Dreiecke zerlegt wird: In völlig analoger Weise ergibt sich die Beziehung
c sin sin b =
b b =
b sin sin g,
und wenn wir dasselbe mit der Höhe auf b machen, erhalten wir
c g,
und wenn wir dasselbe mit der Höhe auf b machen, erhalten wir
c sin sin a =
a a =
a sin sin g.
(Dazu muss man eigentlich gar nichts rechnen, sondern nur die Symbole umbenennen, da die zugrunde liegenden geometrischen Situationen in allen drei Fällen
vollkommen gleich sind). g.
(Dazu muss man eigentlich gar nichts rechnen, sondern nur die Symbole umbenennen, da die zugrunde liegenden geometrischen Situationen in allen drei Fällen
vollkommen gleich sind).
| | | |

Sinus und Cosinus
| |
| | |
Die drei Beziehungen, die wir nun erhalten haben, gelten auch für Dreiecke, die einen rechten oder einen stumpfen Winkel
besitzen. (Für einen Beweis im stumpfwinkeligen Dreieck klicken Sie auf den Button rechts).
Wir haben mit ihnen eine in allen Dreiecken geltende Gesetzmäßigkeit entdeckt.
Sie kann kompakter in der Form
geschrieben werden und trägt den Namen Sinussatz. In Worten kann er so
ausgedrückt werden: In einem Dreieck sind alle drei Verhältnisse
"Seitenlänge dividiert durch Sinus des gegenüberliegenden Winkels" gleich. Daraus folgt, dass sich
zwei Seitenlängen so verhalten wie die Sinuswerte der gegenüberliegenden
Winkeln: Aus (5) ergeben sich
a
b |
= |
sin a a
sin b b |
|
|
(6) |
| | | |
| |
| | |
und die analogen Beziehungen
b/c =
sin b/sin b/sin g
und
c/a =
sin g
und
c/a =
sin g/sin g/sin a.
Diese Beziehungen sind im Umgang mit Dreiecken so wichtig, dass Sie sie auswendig kennen sollten!
Im nebenstehende Applet wird die Bedeutung der verschiedenen Verhältnisse, die in den Varianten (5)
und (6) des Sinussatzes auftreten, anhand eines veränderbaren Dreiecks visualisiert. a.
Diese Beziehungen sind im Umgang mit Dreiecken so wichtig, dass Sie sie auswendig kennen sollten!
Im nebenstehende Applet wird die Bedeutung der verschiedenen Verhältnisse, die in den Varianten (5)
und (6) des Sinussatzes auftreten, anhand eines veränderbaren Dreiecks visualisiert.
Der Sinussatz wird in Vermessungsaufgaben oft benötigt. Darauf werden wir weiter unten in einem
späteren Abschnitt eingehen.
Sinussatz, Flächeninhalt und Umkreisradius
| | | |
Applet
Dreieck und Sinussatz
| |
| | |
Dem Sinussatz entspringt eine Reihe nützlicher Beziehungen und Formeln zur Dreiecksberechnung.
Insbesondere sind die in ihm auftretenden Größen eng verwandt
mit dem Flächeninhalt und dem Umkreisradius eines Dreiecks:
- Flächeninhalt des Dreiecks:
Gemäß Formel (2) ist der Flächeninhalt A eines Dreiecks durch
"Grundlinie × Höhe / / 2"
gegeben. Dabei es es gleichgültig, welche der drei Seiten als Grundlinie gewählt wird.
Damit erhalten wir gleich drei Formeln
A = a 2"
gegeben. Dabei es es gleichgültig, welche der drei Seiten als Grundlinie gewählt wird.
Damit erhalten wir gleich drei Formeln
A = a ha ha / / 2 =
b 2 =
b hb hb / / 2
= c 2
= c hc hc / / 2.
Mit ihrer Hilfe können wir die Dreiecksfläche leicht durch die Seiten und Winkel
ausdrücken: Wir erinnern uns, dass wir bereits oben
hc = b 2.
Mit ihrer Hilfe können wir die Dreiecksfläche leicht durch die Seiten und Winkel
ausdrücken: Wir erinnern uns, dass wir bereits oben
hc = b sin sin a
berechnet haben, woraus sich
A =
b a
berechnet haben, woraus sich
A =
b c c sin sin a a / / 2
ergibt. Durch Anwendung des Sinussatzes (oder durch Berechnung der anderen Höhen) ergeben sich die drei Formeln 2
ergibt. Durch Anwendung des Sinussatzes (oder durch Berechnung der anderen Höhen) ergeben sich die drei Formeln
| A = |
a b b sin sin g g
2 |
= |
b c c sin sin a a
2 |
= |
c a a sin sin b b
2 |
|
|
(7) |
für den Flächeninhalt eines beliebigen Dreiecks. Die Aussage, dass diese drei Ausdrücke gleich sind,
ist lediglich eine andere Formulierung des Sinusatzes: Wird (7) durch
a b b c c / / 2
dividiert, so folgt unmittelbar (5). 2
dividiert, so folgt unmittelbar (5).
- Umkreisradius des Dreiecks:
Der Sinussatz (5) drückt aus, dass in jedem Dreieck die drei Verhältnisse "Seitenlänge dividiert durch Sinus des gegenüberliegenden Winkels" gleich sind.
Hat diese Größe, die also auf dreierlei Arten als der Quotient
"Seitenlänge dividiert durch Sinus des gegenüberliegenden Winkels" berechnet werden kann, eine geometrische Bedeutung?
Ja - interessanterweise ist sie gleich dem Durchmesser des Umkreises, d.h. dem
Doppelten des Umkreisradius R.
Daher wird der Sinussatz auch manchmal in der Form
a
sin a a |
= |
b
sin b b |
= |
c
sin g g |
= |
2R |
|
|
(8) |
angeschrieben. Der Beweis (siehe den Button rechts, falls er Sie interessiert) benötigt den Peripheriewinkelsatz, auf den wir
weiter unten zu sprechen kommen.
Wir werden später eine weitere Formel für den Umkreisradius angeben, siehe (12).
Sinussatz und Ähnlichkeit
| | | |
| |
| | |
Am Sinussatz lassen sich sehr schön die Ähnlichkeitseigenschaften ebener geometrischer Figuren demonstrieren:
Betrachten wir irgendein Dreieck mit beliebigen Seitenlängen und Winkeln, und betrachten wir
dazu ein ähnliches, d.h. um einen beliebigen Faktor q
"aufgeblasenes" oder "geschrumpftes" Dreieck. Der Sinussatz gilt natürlich für beide Dreiecke.
Gehen Sie noch einmal zu den Formeln (5) und (6) zurück und überzeugen Sie sich,
dass sie auch dann gültig bleiben, wenn jede Seitenlänge durch ihr
q-faches ersetzt, die Winkel aber gleich
gelassen werden! Insbesondere (6) illustriert auf diese Weise, dass Seitenverhältnisse in ähnlichen
Figuren übereinstimmen.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Der wohl bekannteste mathematische Satz über Dreiecke ist der Satz von Pythagoras. Er gilt aber nur in rechtwinkeligen
Dreiecken: Ist beispielsweise der der Seite c
gegenüberliegende Winkel g gleich 90°,
so gilt
c2 = a2 + b2.
(Sie werden gleich sehen, warum wir ihn "verkehrt herum" schreiben).
Besitzt dieser Satz eine Verallgemeinerung, die in beliebigen Dreiecken gilt?
Ja, eine solche Verallgemeinerung existiert, und es ist gar nicht schwer, sie zu finden.
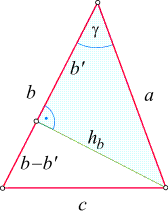 Betrachten wir zuerst ein spitzwinkeliges Dreieck. Ähnlich wie
bei der obigen Herleitungs des Sinussatzes zerlegen wir es in zwei rechtwinkelige Dreiecke, wobei
wir nun die Höhe auf die Seite b
dazu benutzen. Wie in der nebenstehenden Skizze bezeichnen wir die Länge der Kathete des oberen (hellblauen)
rechtwinkeligen Dreiecks, die einen Abschnitt der Seite b
darstellt, mit b'.
Unser Ziel ist es nun, c zu berechnen,
wenn a, b
und g bekannt sind. Dazu verwenden wir zwei uns bereits bekannte
Beziehungen:
Betrachten wir zuerst ein spitzwinkeliges Dreieck. Ähnlich wie
bei der obigen Herleitungs des Sinussatzes zerlegen wir es in zwei rechtwinkelige Dreiecke, wobei
wir nun die Höhe auf die Seite b
dazu benutzen. Wie in der nebenstehenden Skizze bezeichnen wir die Länge der Kathete des oberen (hellblauen)
rechtwinkeligen Dreiecks, die einen Abschnitt der Seite b
darstellt, mit b'.
Unser Ziel ist es nun, c zu berechnen,
wenn a, b
und g bekannt sind. Dazu verwenden wir zwei uns bereits bekannte
Beziehungen:
- Im unteren (weißen) Dreieck gilt nach dem Satz von Pythagoras
c2 = hb2 + (
 b - b' b - b' )2. )2.
- Im oberen (hellblauen) Dreieck schreiben wir die Definitionen von Sinus und Cosinus des
Winkels g in der Form
hb = a
 sin sin g
und
b' = a g
und
b' = a cos cos g
an. g
an.
Die letzten beiden Beziehungen setzen wir in den Ausdruck für c2
ein und erhalten
c2 = a2 sin2 sin2 g +
(b -
a g +
(b -
a cos cos g)2.
Damit ist das Ziel eigentlich erreicht (c durch
a, b
und g auszudrücken). Der erhaltene Ausdruck für
c2 lässt sich noch ein bisschen verschönern, indem
die Klammer ausmultipliziert und die Identität
sin2 g)2.
Damit ist das Ziel eigentlich erreicht (c durch
a, b
und g auszudrücken). Der erhaltene Ausdruck für
c2 lässt sich noch ein bisschen verschönern, indem
die Klammer ausmultipliziert und die Identität
sin2 g +
cos2 g +
cos2 g = 1
benutzt wird: g = 1
benutzt wird:
c2 = a2 sin2 sin2 g +
b2 - 2 g +
b2 - 2 a a b b cos cos g +
a2cos2 g +
a2cos2 g
= a2 + b2 - 2 g
= a2 + b2 - 2 a a b b cos cos g. g.
Unser Resultat lautet also:
c2 = a2 + b2 - 2 a a b b cos cos g.
Es kann dazu benutzt werden, c
zu berechnen, wenn die beiden anderen Seitenlängen und der der Seite c
gegenüberliegende Winkel g bekannt sind. g.
Es kann dazu benutzt werden, c
zu berechnen, wenn die beiden anderen Seitenlängen und der der Seite c
gegenüberliegende Winkel g bekannt sind.
Die gleiche Argumentation kann durchgespielt werden, wenn das gegebene Dreieck durch eine der beiden anderen Höhen
zerlegt wird. Dazu muss man gar nichts rechnen, sondern nur die Symbole umbenennen, da die zugrunde liegenden geometrischen Situationen in allen drei Fällen
vollkommen gleich sind. Die gleichen Resultate ergeben sich auch für stumpfwinkelige Dreiecke.
(Für einen Beweis klicken Sie auf den Button rechts).
Damit haben wir drei Beziehungen gefunden, die in jedem Dreieck gelten:
| | | |
| |
| | |
|
|
(9 ' ' ) ) |
|
|
(9 '' '' ) ) |
Sie werden unter dem Namen Cosinussatz zusammengefasst.
In jeder dieser drei Formeln wird das Quadrat der Länge einer Seite durch den Cosinus des ihr gegenüberliegenden Winkels und
die Längen der beiden anderen Seiten ausgedrückt.
Wenn Sie mit Vektoren vertraut sind und den Begriff des Skalarprodukts kennen, können
Sie mit Hilfe des nebenstehenden Buttons einen kürzeren und eleganteren Beweis des Cosinussatzes
aufrufen.
| | | |

Skalarprodukt
mit Vektoren
| |
| | |
Spezialfälle:
- Da cos
 ( ( 90° 90° ) = 0
ist, folgt: Ist einer der Winkel ein rechter, so reduziert sich diejenige Formel, die seinen Cosinus enthält,
auf den Satz von Pythagoras.
Ist etwa g = 90°, so wird (9)
zur Aussage c2 = a2 + b2.
Worauf reduzieren sich in diesem Fall die Beziehungen ( ) = 0
ist, folgt: Ist einer der Winkel ein rechter, so reduziert sich diejenige Formel, die seinen Cosinus enthält,
auf den Satz von Pythagoras.
Ist etwa g = 90°, so wird (9)
zur Aussage c2 = a2 + b2.
Worauf reduzieren sich in diesem Fall die Beziehungen ( 9 9 ' ' ) und
( ) und
( 9 9 ' ' ' ' )? )?
- Eine interessante Folgerung ergibt sich auch, wenn wir den Grenzfall eines
"zusammengeklappten" (oder "ausgearteten") Dreiecks betrachten, in dem einer der Winkel 0 ist.
Setzen wir etwa g = 0 und verwenden
cos
  0 0 = 1,
so reduziert sich (9) auf die Aussage c2 = (a - b)2.
Können Sie interpretieren, was das bedeutet?
Worauf reduzieren sich die Beziehungen ( = 1,
so reduziert sich (9) auf die Aussage c2 = (a - b)2.
Können Sie interpretieren, was das bedeutet?
Worauf reduzieren sich die Beziehungen ( 9 9 ' ' ) und
( ) und
( 9 9 ' ' ' ' )? )?
Ebenso wird der Sinussatz wird der Cosinussatz in Vermessungsaufgaben oft benötigt. Darauf werden wir weiter unten
im nächsten Abschnitt eingehen.
Berechnung von Winkeln aus Längen
| | | |
| |
| | |
Der Cosinussatz kann nicht nur zur Berechnung von Seitenlängen verwendet werden.
So erlaubt es die aus (9) folgende Beziehung
den Cosinus des Winkels g zu ermitteln, wenn alle
Seitenlängen des Dreiecks bekannt sind. Ist
cos g
bekannt, so kann
g eindeutig als der Arcus Cosinus dieses Werts
bestimmt werden. Analoge Beziehungen für die anderen Winkel entstehen durch entsprechende Umbenennungen der Symbole. g
bekannt, so kann
g eindeutig als der Arcus Cosinus dieses Werts
bestimmt werden. Analoge Beziehungen für die anderen Winkel entstehen durch entsprechende Umbenennungen der Symbole.
Das ist nicht nur nützlich für Berechnungen an Dreiecken, sondern illustriert, dass der
Winkelbegriff aus dem Längenbegriff abgeleitet ist.
Bereits die Festlegung eines Winkels im Bogenmaß oder die Definition der
Winkelfunktionen im rechtwinkeligen Dreieck beziehen sich auf Längen und
Längenverhältnisse. Im Cosinussatz wird das auf besonders schöne und
allgemeingültige Weise noch einmal deutlich deutlich:
Da beliebige durch Strecken oder Geraden begrenzte ebene Figuren in Dreiecke zerlegt werden
können, können mit Hilfe des Cosinussatzes alle in solchen Figuren auftretenden Winkel
bestimmt werden. Die weitergehende Zerlegung von schiefwinkeligen in rechtwinkelige
Dreieck ist dabei nicht mehr notwendig, da sie gewissenmaßen in der Herleitung des Cosinussatzes bereits
ein für allemal durchgeführt wurde.
Analog zum oben besprochenen Sinussatz lassen sich die Ähnlichkeitseigenschaften ebener geometrischer Figuren
auch anhand des Cosinussatzes demonstrieren:
Gehen Sie noch einmal zu den Formeln (9) bis (10) zurück und überzeugen Sie sich,
dass sie auch dann gültig bleiben, wenn jede Seitenlänge durch ihr
q-faches ersetzt, die Winkel aber gleich
gelassen werden!
|
| | |

Sinus und Cosinus
im rechtwinkeligen Dreieck
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Vermessungsaufgaben bestehen darin, gewisse Größen in geometrischen Figuren, die aus Dreiecken bestehen
oder sich in Dreiecke zerlegen lassen, aus gewissen anderen numerisch bekannten Größen zu
errechnen. Oft handelt es sich dabei um mehr oder weniger realistische Situationen aus der Landvermessung.
Zum Lösen dieser Aufgaben ist manchmal eine Kombination von Argumenten nötig.
Sie zu finden, ist nicht immer leicht. Daher geben wir hier eine ausführliche Liste von
Tipps, fassen zusammen, wie Dreiecke "aufgelöst" werden und besprechen einige Beispiele.
Einige Tipps
| | | |
| |
| | |
Mit dem nebenstehenden Button können Sie einige Tipps zur Bearbeitung von Vermessungsaufgaben aufrufen.
Darunter finden Sie Hinweise zur sinnvollen Nutzung der Werkzeuge
mathe online Mini-Rechner
und JavaCalc für numerische
Berechnungen, die Winkelfunktionen und die Umrechnungefaktoren zwischen
Grad- und Bogenmaß enthalten.
Auflösen von Dreiecken
| | | |
| |
| | |
Die wichtigsten Bestimmungsstücke eines Dreieck sind die Seitenlängen und die Winkel.
Von diesen sechs Größen reichen (bis auf Mehrdeutigkeiten, die
in praktischen Aufgaben leicht in den Griff zu bekommen sind) drei aus, um ein Dreieck
festzulegen.
Unter dem "Auflösen von Dreiecken" versteht man die Kunst, aus drei gegebenen Bestimmungsstücken
die restlichen drei zu berechnen. Mit dem nebenstehenden Button erhalten Sie eine Hilfe zur
Vorgangsweise beim Auflösen von Dreiecken. Sie enthält
- eine Tabelle der möglichen Fälle gegebener Größen
(die mit den Kürzeln SWW, SSW, SWS, und SSS bezeichnet werden) und der Methoden
zur Berechnung der restlichen Bestimmungsstücke, sowie
- eine kurze Besprechung der Mehrdeutigkeiten, die mit Dreiecksangaben verbunden sein können.
Beispiele für Vermessungsaufgaben
| | | |
von Dreiecken
| |
| | |
Wir besprechen nun drei Vermessungsaufgaben (mit ansteigendem Schwierigkeitsgrad).
Klicken Sie die Links unter den Skizzen bzw. im Text an, um Hinweise
zu den einzelnen Lösungsschritten hervorzuheben.
In den Skizzen sind bekannte (gegebene oder bereits berechnete) Größen rot und gelb, die
aus ihnen im jeweiligen Schritt zu berechnenden Größen blau und türkisfarbig dargestellt.
Numerische Berechnungsresultate werden sinnvoll gerundet.
- Aufgabe:
Die in der folgenden Skizze strichliert eingezeichnete Breite eines Gewässers soll bestimmt werden.
Lösung:
- Schritt 1: Zuerst legen wir eine Skizze an, in der die Größen durch Symbole
gekennzeichnet sind. Gegeben sind
a = 125
 m,
b = 21.3° und
g = 103.5°.
Gesucht ist x. m,
b = 21.3° und
g = 103.5°.
Gesucht ist x.
- Schritt 2: Wir zeichnen den dritten Winkel a
ein und berechnen ihn (Winkelsumme im Dreieck = 180°
 !) zu
a = 180° - 21.3 - 103.5° =
55.2°. Nun kann x mit Hilfe des
Sinussatzes bestimmt werden:
x/sin !) zu
a = 180° - 21.3 - 103.5° =
55.2°. Nun kann x mit Hilfe des
Sinussatzes bestimmt werden:
x/sin b = a/sin b = a/sin a,
daher
x = a a,
daher
x = a sin sin b b /sin /sin a =
125 a =
125 m · sin(21.3°) m · sin(21.3°) /sin(55.2°) =
55.3 /sin(55.2°) =
55.3 m. m.
Die gesuchte Breite des Flusses ist 55.3 m. m.
- Aufgabe:
Von dem in der folgenden Skizze dargestellten Parallelogramm sind gegeben:
a = 7.2,
f = 5.5 und
a = 47°.
Gesucht sind die Seite b sowie die
Winkel b und e
(wobei e < 90°
vorausgesetzt ist).
Lösung:
- Schritt 1: Aufgrund der Parallelogramm-Eigenschaft (gegenüberliegende Seiten
sind zueinander parallel) wird der Winkel b durch
a zu 180° ergänzt, ergibt sich daher unmittelbar zu
b = 180° - a =
180° - 47° = 133°.
- Schritt 2: Der Sinus des Winkels e ergibt sich gemäß dem
Sinussatz zu
sin
 e e / / a
= sin a
= sin a a / / f,
woraus
sin f,
woraus
sin e
= (a e
= (a / / f f ) ) sin sin a =
(7.2/5.5) a =
(7.2/5.5) sin(47°) = 0.9574 und
daraus
e = asin( sin(47°) = 0.9574 und
daraus
e = asin( 0.9574 0.9574 ) = 73.22°
folgt. ) = 73.22°
folgt.
- Schritt 3: Nachdem der zusätzlich benannte Winkel d
zu 180° - a - e =
59.78° bestimmt ist (Winkelsumme im Dreieck = 180°
 !), kann
die Seite b
durch eine nochmalige Anwendung des Sinussatzes ermittelt werden:
b/sin !), kann
die Seite b
durch eine nochmalige Anwendung des Sinussatzes ermittelt werden:
b/sin d = f d = f /sin /sin a,
daher
b = f a,
daher
b = f sin sin d d /sin /sin a =
5.5 a =
5.5 sin(59.78°) sin(59.78°) /sin(47°) =
6.499. /sin(47°) =
6.499.
Bemerkung: In Schritt 3 hätte man anstelle des Sinussatzes den Cosinussatz anwenden und b
aus a, f
und d bestimmen können.
Eine weitere Alternative hätte darin bestanden, b mit Hilfe des Sinussatzes
aus a, e und d zu bestimmen.
Führen Sie diese Rechnungen zur Übung selbst durch!
Zusatzaufgabe: Was ändert sich, wenn die Bedingung e < 90°
nicht gestellt wird?
- Aufgabe:
Durch einen Berg soll ein Stollen getrieben werden. Der Berg und die Wetterlage verhindern Winkelmessungen, so dass
die Lage des Stollens durch folgende Skizze, die nur Längenangaben enthält, festgelegt werden muss.
Dabei ist a = 985 m,
b = 786 m,
b = 786 m,
c = 734 m,
c = 734 m und
x = 352 m und
x = 352 m.
Wie groß ist der Winkel e m.
Wie groß ist der Winkel e ? ?
Lösung:
- Schritt 1: Wir sind an dem (nun hellblau hervorgehobenen) Dreieck interessiert, das
den Winkel e enthält und bezeichnen
den einzigen Winkel dieses Dreiecks, der unmittelbar aus den bisher bekannten Größen berechnet werden kann,
mit a.
- Schritt 2: a kann mit Hilfe des Cosinussatzes
aus den Längen a, b
und c berechnet werden:
cos
 a
= (a2 + c2 - b2)/(2 a
= (a2 + c2 - b2)/(2 a a c) =
0.6163,
daher
a = acos(0.6163) =
51.95°. c) =
0.6163,
daher
a = acos(0.6163) =
51.95°.
- Schritt 3: Wir bezeichnen die Länge der Strecke, auf der der Stollen liegt, mit
y. Nun, da a bekannt ist,
kann y mit Hilfe des Cosinussatzes aus
c, x und
a berechnet werden:
y2 = c2 + x2
- 2
 c c x x cos cos a, was auf
y = 586.67 a, was auf
y = 586.67 m
führt. m
führt.
- Schritt 4: Zuletzt kann der gesuchte Winkel e
mit Hilfe des Sinussatzes aus x,
y und a
bestimmt werden. Führen Sie die Rechnung selbst durch!
Sie sollten als Resultat e = 28.20°
erhalten.
Bemerkung: In Schritt 4 hätte man als Alternative den Cosinussatz
anwenden können, um e aus
c, x
und y zu bestimmen. Führen Sie diese Rechnung zur Übung ebenfalls durch!
Falls Sie sich im Rahnmen Ihrer Ausbildung mit Vermessungsaufgaben beschäftigen müssen, werden Sie mit diesem Gebiet umso weniger
Schwierigkeiten haben, je besser es Ihnen gelingt, die grundlegenden Methoden und prinzipiellen Vorgangsweisen
zu verstehen. Daher unser letzter Tipp: Üben ist zwar wichtig - kehren Sie aber
bei Verständnisproblemen mit den Ihnen gestellten Aufgaben auch zu den Grundlagen,
wie sie hier dargestellt wurden, zurück und frischen Sie ihr Wissen darüber auf!
|
| | |
| |
| | |
| Einige weitere Resultate der Dreiecksgeometrie |
| | | |
Zum Seitenanfang | |
| | |
Die bereits Jahrtausende währende Beschäftigung mit der Geometrie der Dreiecke
hat zahlreiche Sätze und Beziehungen zwischen Dreieckgrößen hervorgebracht.
Hier wollen wir (zum Teil ohne Beweis) einige Resultate, die in konkreten Berechnungen
nützlich sein können, nachtragen. Hier eine Liste der nachfolgenden Themen:
Wenn nicht anders angegeben, entsprechen die
Bezeichnungen der Seiten und Winkel der obigen Konvention.

Kongruenzsätze
Manchmal möchte man schnell erkennen, ob zwei Dreieck nur verdrehte und verschobene
Versionen voneinander sind. Dabei kann man sich folgender Regeln (Kongruenzsätze)
bedienen: Zwei Dreiecke sind kongruent (deckungsgleich), wenn sie
- in allen drei Seiten übereinstimmen (SSS-Satz).
- in zwei Seiten und den von ihnen eingeschlossenen Winkel übereinstimmen (SWS-Satz).
- in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel
übereinstimmen (SSW-Satz).
(Stimmen zwei Dreiecke in zwei Seiten und dem der kleineren Seite gegenüberliegenden Winkel
überein, so müssen die Dreiecke nicht kongruent sein
- überlegen Sie sich ein Beispiel dazu!)
- in einer Seite und zwei Winkeln übereinstimmen (WSW- und SWW-Satz).

Ähnlichkeitssätze
Zwei Dreiecke sind genau dann zueinander ähnlich, wenn sie in zwei (und damit automatisch in allen drei) Winkeln
übereinstimmen. Das ist genau dann der Fall, wenn ihre Seitenlängen
zueinander proportional sind
(d.h. wenn a : : b b : : c =
a' c =
a' : : b' b' : : c',
wobei die "ungestrichenen" Symbole zum einen, die "gestrichenen" Symbole zum anderen Dreieck gehören). c',
wobei die "ungestrichenen" Symbole zum einen, die "gestrichenen" Symbole zum anderen Dreieck gehören).

Katheten- und Höhensatz
In
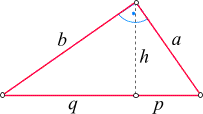 einem rechtwinkeligen Dreieck sei h
die Höhe auf die Hypotenuse, und seien p und
q die gemäß der
nebenstehenden Skizze definierten Hypotenusenabschnitte.
Die Länge der Hypotenuse ist
c = p + q.
Dann gilt:
einem rechtwinkeligen Dreieck sei h
die Höhe auf die Hypotenuse, und seien p und
q die gemäß der
nebenstehenden Skizze definierten Hypotenusenabschnitte.
Die Länge der Hypotenuse ist
c = p + q.
Dann gilt:
- Kathetensatz: a2 = p
 c
und b2 = q c
und b2 = q c. c.
Hierbei handelt es sich um eine Erweiterung des Satzes von Pythagoras, denn aus dem
Kathetensatz folgt
a2 + b2 = (p + q) c =
c2. c =
c2.
- Höhensatz: h2 = p
 q. q.
Gemeinsam mit dem Kathetensatz folgt aus ihm, dass
h = a b b / / c. c.

| | | |
Geometrische
Deutung des
| |
| | |
Peripheriewinkelsatz
Er
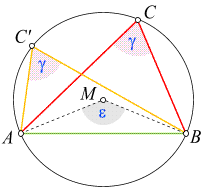 besagt: Zwei Peripheriewinkel über demselben, von zwei Punkten begrenzten
Kreisbogen sind gleich groß. Ist der zugehörige Zentriwinkel (Mittelpunktswinkel) e,
so ist der gemeinsame Peripheriewinkel entweder durch e/2 oder durch
180° - e/2 gegeben,
je nachdem, ob der Kreisbogen größer oder kleiner als der Halbkreisbogen
ist. Für den Halbkreisbogen (e = 180°) führen beide Formeln zum gleichen Resultat.
besagt: Zwei Peripheriewinkel über demselben, von zwei Punkten begrenzten
Kreisbogen sind gleich groß. Ist der zugehörige Zentriwinkel (Mittelpunktswinkel) e,
so ist der gemeinsame Peripheriewinkel entweder durch e/2 oder durch
180° - e/2 gegeben,
je nachdem, ob der Kreisbogen größer oder kleiner als der Halbkreisbogen
ist. Für den Halbkreisbogen (e = 180°) führen beide Formeln zum gleichen Resultat.
Der erste dieser Fälle ist in der nebenstehenden Skizze veranschaulicht. Gegeben sind die Kreislinie sowie die Punkte
A und B,
und es gilt:
- Von jedem Punkt des oberen (größeren) Kreisbogens aus betrachtet, "sieht" man die Strecke
AB unter dem gleichen
Peripheriewinkel g.
- Der Zentriwinkel ist e = 2
 g. g.
Klicken Sie hier, um Anhaltspunkte für
einen Beweis in der Skizze einzublenden: Da die drei strichlierten Strecken Radien des Kreises bilden,
sind sie alle gleich lang. Daher besteht die dem Kreis eingeschriebene Figur aus drei
gleichschenkeligen Dreiecken. Insbesondere kommen die Winkel
a und b
je zweimal vor.
Nun gilt
- d = 180° - 2a
- w = 180° - 2b
- Mit diesen Informationen berechnen wir den Zentriwinkel zu
e = 360° - d - w =
360° - (180° - 2a) - (180° - 2b) =
2(a + b),
was genau gleich 2 g, dem
Doppelten des Peripheriewinkels ist. Daher gilt: g = e/2. g, dem
Doppelten des Peripheriewinkels ist. Daher gilt: g = e/2.
Dieses Resultat ist unabhängig von der konkreten Lage des Punktes C auf dem oberen Kreisbogen.
Damit ist der Satz für den oberen (größeren) Kreisbogen bewiesen.
Beweisen Sie zur Übung selbst, dass sich alle Peripheriewinkel
für den unteren (kleineren) Kreisbogen zu
180° - e/2 ergeben!
Für einen Halbkreisbogen (e = 180°) ergibt sich
g = 90°, d.h. jeder Peripheriewinkel ist
ein rechter! Auf diese Weise ergibt sich der oben besprochene Satz von Thales
als Spezialfall des Peripheriewinkelsatzes.
Die Umkehrung des Peripheriewinkelsatzes lautet: Die Menge Punkte, von denen aus man eine gegebene Strecke unter einem
dem gegebenen Winkel g sieht, bildet ein
Kreisbogenpaar (das Sie sich mit Hilfe des nebenstehenden Buttons ansehen können).

| | | |
Kreisbogenpaar
| |
| | |
Flächeninhaltsformeln
Zusätzlich zu (2) und (7) steht eine Reihe weiterer Formeln für den Flächeninhalt eines Dreiecks
zur Verfügung. Hier eine Auswahl:
= 2 R R 2 2 sin sin a
sin a
sin b
sin b
sin g = g = |
a b b c c
4 R R |
, |
|
(11) |
wobei R der Umkreisradius ist.
Analoge Varianten der ersten Formel fär andere Seiten-Winkel-Kombinationen entstehen durch entsprechende Umbenennung
der Symbole.
Siehe auch Formel (12) für einen Zusammenhang zwischen Fläche und Inkreisradius
sowie die Heronsche Flächenformel (14).

Umkreisradius
Neben (8) kann der Umkreisradius eines beliebigen Dreiecks aus den Seitenlängen und dem Flächeninhalt
A mit Hilfe der Formel
berechnet werden. Im rechtwinkeligen Dreieck mit Hypotenuse c ist
R = c / / 2. 2.

Inkreisradius
Wird mit s = (a + b + c) / / 2
der halbe Umfang eines beliebigen Dreiecks und mit
A sein Flächeninhalt bezeichnet,
so ist der Inkreisradius durch 2
der halbe Umfang eines beliebigen Dreiecks und mit
A sein Flächeninhalt bezeichnet,
so ist der Inkreisradius durch
gegeben. Siehe auch die unten wiedergegebene die Heronsche Formel (15) für den Inkreisradius.
Im rechtwinkeligen Dreieck mit Katheten a, b und
Hypotenuse c ist
r = (a + b - c) / / 2. 2.

Heronsche Formeln
Sei s = (a + b + c) / / 2
der halbe Umfang eines beliebigen Dreiecks. Dann gilt: 2
der halbe Umfang eines beliebigen Dreiecks. Dann gilt:
- Heronsche Flächenformel:
| A =
|
_________________
Ö s (s -
a) (s -
a) (s - b) (s - b) (s
- c) (s
- c)
|
|
(14) |
- Heronsche Formel für den Inkreisradius:
| r =
|
Ö |
________________
(s - a) (s
- b) (s
- b) (s - c) (s - c)
s
|
|
(15) |
Diese Formeln sind nach dem antiken Mathematiker Heron von Alexandria, der im 1. Jahrhundert lebte, benannt.

Tangenssatz
In jedem Dreieck gilt
a
+ b
a - b |
= |
tan ((a
+ b ((a
+ b ) ) /2) /2)
tan ((a
- b ((a
- b ) ) /2) /2) |
= |
cot (g (g /2) /2)
tan ((a
- b ((a
- b ) ) /2) /2) |
. |
|
(16) |
Zwei analoge Formeln für andere Seiten-Winkel-Kombinationen entstehen durch entsprechende Umbenennung der Symbole.

Lage von Punkten im Dreieck
Die Lage (Position) von Punkten (wie Höhenschnittpunkt, Schwerpunkt, Um- und Inkreismittelpunkt)
kann mit den Methoden der Vektorrechnung ermittelt werden.
Insbesodere ist der Ort des Schwerpunkts durch eine ganz einfache Formel bestimmt.
Darauf wird im ersten Vektor-Kapitel näher eingegangen.

| | | |

Schwerpunkt des Dreiecks
| |
| | |
Ungleichungen im Dreieck
In jedem Dreieck ist
- die Summe zweier Seiten stets größer als die dritte Seite.
- der Betrag der Differenz zweier Seiten stets kleiner als die dritte Seite.
In Formeln: a + b > c,
| a - b a - b | < c
sowie vier weitere Ungleichungen, die durch entsprechende Umbenennung der Symbole entstehen. | < c
sowie vier weitere Ungleichungen, die durch entsprechende Umbenennung der Symbole entstehen.

Trigonometrischer Monotoniesatz
In jedem Dreieck liegt der größte Winkel der größten Seite, der kleinste Winkel der
kleinsten Seite gegenüber.
So ist beispielsweise a < b < c
genau dann, wenn a < b < g.

Eine weitere Beziehung ... ...
... sei stellvertretend für viele andere genannt: In jedem Dreieck gilt sei stellvertretend für viele andere genannt: In jedem Dreieck gilt

Die Fülle der Resultate, die im Laufe der Geschichte erzielt wurden, illustriert nicht nur die praktische Nützlichkeit der
Dreiecksgeometrie, sondern auch die die Faszination, diese Disziplin auf Menschen ausgeübt hat und
- noch immer - ausübt.
Wenn Sie mehr über das Thema wssen wollen, finden Sie in unserer
Ressourcensammlung Mathe-Links und Online-Werkzeuge
unter der Kategorie Mathematische Einzelthemen > Winkelfunktionen und Trigonometrie
zahlreiche weitere Materialien. Als umfangreiche Formelsammlungen empfehlen wir
Ebene Trigonometrie (aus Desktop Bronstein) und
Dreiecke (aus Desktop Mathematik)
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Das in diesem Kapitel bisher behandelte Gebiet der Geometrie heißt, streng genommen,
"ebene Trigomometrie", da es von Dreiecken in der Ebene handelt.
Dabei denken wir zunächst an die Zeichenebene, aber alle hier
gewonnenen Erkenntnisse lassen sich auch auf Dreiecke anwenden,
die in beliebigen Ebenen des Raumes liegen. Ihr liegen die
Vorstellungen der "euklidischen" Geometrie zugrunde.
Eine damit verwandte Disziplin studiert "Dreiecke", die auf Sphären,
d.h. auf Kugeloberflächen leben - die
"sphärische Trigomometrie".
Sie ist ein Beispiel für eine Art, Geometrie zu betreiben, der "nicht-euklidische"
Vorstellungen zugrunde liegen. Wir wollen hier nicht ausführlich auf
dieses Gebiet eingehen, sondern nur einige Grundgedanken und Resultate skizzieren.
Was ist ein "Dreieck" auf einer Sphäre? Um es kurz zu machen, notieren wir dazu ein paar Definitionen:
- Wir betrachten eine Kugel mit Mittelpunkt M und
Radius r und
wollen nun Figuren, die auf ihrer Oberfläche (Sphäre) liegen, studieren.
- Eine Schnittlinie zwischen der Sphäre und einer Ebene, die M
enthält, wird als Großkreis bezeichnet. Großkreise sind in der sphärischen Geometrie das,
was in der ebenen Geometrie die Geraden sind.
- Die Schnittlinien zwischen der Sphäre und Ebenen die M
nicht enthalten (so genannte Kleinkreise), sind das, was in der ebenen Geometrie die Kreise sind.
- Zwei (verschiedene) Punkte auf der Sphäre definieren einen eindeutigen Großkreis, auf dem
sie liegen, und teilen diesen in zwei Großkreisbögen, von denen der kürzere die
kürzeste Verbindung der beiden Punkte (auf der Sphäre) darstellt.
- Werden drei Punkte der Sphäre, die nicht in einer Ebene liegen, durch drei
Großkreisbögen verbunden, so entsteht ein sphärisches Dreieck oder Kugeldreieck.
Die drei Großkreisbögen werden als Seiten bezeichnet, ihre Längen als
Seitenlängen. Die Innenwinkel, unter denen die Seiten einander schneiden, sind
die Winkel des sphärischen Dreiecks.
- Die Bezeichnungskonventionen für sphärische Dreiecke sind analog zu den oben besprochenen:
Der Winkel a liegt der Seite a gegenüber
usw.
Die schönste Anwendung dieser Idee ist die "Himmelsspäre", auf der Himmelsobjekte wie Sterne als Eckpunkte von
sphärischen Dreiecken aufgelasst werden können. Die sphärische Trigonometrie entstand historisch
vor allem aus der Frage, wie die Orte von Himmelsobjekten
gemessen und in Zahlen festgehalten werden können. Daher bildet sie die mathematische Grundlage der
Himmelsvermessung, und angehende AstronomInnen lernen sie gleich zu Beginn ihres Studiums kennen.
Ein zweites Anwendungsgebiet stellt die (als exakte Sphäre idealisierte) Erdoberfläche dar,
und in den technischen und ingenieurwissenschaftlichen Fächern ergeben sich weitere.
Auf der Sphäre läßt sich ebenso Geometrie betreiben wir in der Ebene.
Was man dabei herausfindet, unterscheidet sich allerdings
- zum Teil auf überraschende Weise -
von den entsprechenden "ebenen" oder "euklidischen" Gesetzmäßigkeiten.
Zählen wir einige Resultate stichwortartig auf:
| | | |

euklidische Geometrie
| |
| | |
Zahlreiche weitere Sätze (solche, die die Resultate der ebenen Trigonometrie verallgemeinern und solche,
die in der Ebene keine Entsprechung haben) lassen sich angeben.
Ebene Trigomonetrie als Grenzfall:
Ein Dreieck, dessen Seitenlängen sehr viel kleiner als der
Radius r der Sphäre ist, ist "fast eben".
Für solche Dreiecke gelten die in diesem Kapitel besprochenen Sätze der ebenen Trigonometrie näherungsweise.
Im "Grenzfall r ® ¥"
("unendlich große Sphäre") werden sie exakt:
So geht beispielsweise die Beziehung (18) in
den Pythagoräischen Satz c2 = a2 + b2
und (19) in den Sinussatz über.
Interessant ist in diesem Zusammenhang auch die Flächenformel (20):
Für ein Dreieck mit gegebenen Seitenlängen wird der sphärische Exzess im
"Grenzfall r ® ¥"
immer kleiner (die Winkelsumme nähert sich immer näher an p, also 180°, an), während der Faktor
r 2
unbeschränkt anwächst. Das Produkt dieser beiden Größen benimmt sich aber recht anständig und wird schließlich
zum Flächeninhalt des ebenen Dreiecks mit den gegebenen Seitenlängen.
Die Techniken, die nötig sind, solche Grenzübergänge rechnerisch durchzuführen
(vor allem die so genannten Reinenentwicklungen)
werden allerdings erst in späteren Kapiteln behandelt. 2
unbeschränkt anwächst. Das Produkt dieser beiden Größen benimmt sich aber recht anständig und wird schließlich
zum Flächeninhalt des ebenen Dreiecks mit den gegebenen Seitenlängen.
Die Techniken, die nötig sind, solche Grenzübergänge rechnerisch durchzuführen
(vor allem die so genannten Reinenentwicklungen)
werden allerdings erst in späteren Kapiteln behandelt.
Für den Fall, dass Sie mehr über dieses Gebiet wissen wollen (oder lernen müssen), finden Sie in unserer
Ressourcensammlung Mathe-Links und Online-Werkzeuge
unter der Kategorie Mathematische Einzelthemen > Winkelfunktionen und Trigonometrie
weiterführende Literatur zur sphärischen Geometrie.
Als umfangreiche Formelsammlung empfehlen wir Sphärische Trigonometrie
aus DeskTop Bronstein.
|
| | |

Grenzwerte reeller Funktionen

Reihenentwicklungen
| |