|  | |
| Strecke | Gerade |
 |  | |
| Strecke | Gerade |
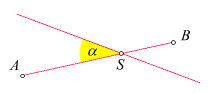 | 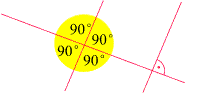 | |
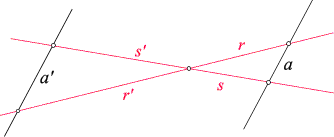
Eine Strecke und eine Gerade: Sie besitzen einen Schnittpunkt S und schließen den Winkel a ein. | Rechter Winkel (rechts das für einen rechten Winkel übliche Symbol) |
| Figur | Flächeninhalt | Skizze |
| Quadrat | A = a2 | 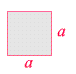 |
| Rechteck | A = ab | 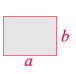 |
| Rechtwinkeliges Dreieck | A = ab/2 |  |
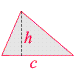
| Beliebiges Dreieck | A = ch/2 ("Grundlinie mal Höhe halbe") |
 |
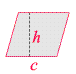
| Parallelogramm | A = ch ("Grundlinie mal Höhe") |
 |


|
|
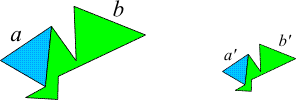
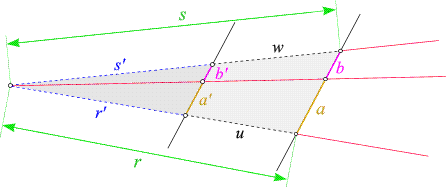
| Satz: Zwei rechtwinkelige Dreiecke, die neben dem rechten noch einen anderen Winkel gemeinsam haben, sind zueinander ähnlich. |
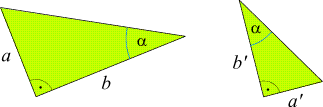
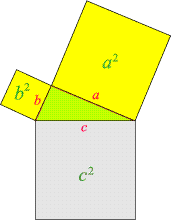
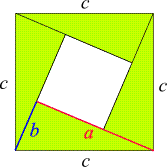
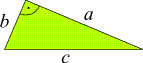 was er bedeutet.
Er ist eine Aussage über eine Beziehung der Seitenlängen jedes rechtwinkeligen Dreiecks.
Werden die Längen der Katheten (d.h. der Seiten, die den rechten Winkel einschließen) mit
a und b
bezeichnet und die Länge der Hypotenuse (d.h. der Seite, die dem rechten Winkel gegenüber liegt) mit
c, so lautet er
was er bedeutet.
Er ist eine Aussage über eine Beziehung der Seitenlängen jedes rechtwinkeligen Dreiecks.
Werden die Längen der Katheten (d.h. der Seiten, die den rechten Winkel einschließen) mit
a und b
bezeichnet und die Länge der Hypotenuse (d.h. der Seite, die dem rechten Winkel gegenüber liegt) mit
c, so lautet er
|