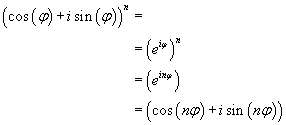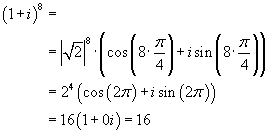Aus der Eulerschen Formel folgt nach den Gesetzen der Potenzrechnung folgender Satz für ganzzahlige Exponenten n:

(1)

denn es gilt

Wendet man den Satz (1) auf eine beliebige komplexe Zahl z = |z|·e^i·f an, so bekommt man die Formel

(2)

für das Potenzieren komplexer Zahlen.

Man hätte das Beispiel auch unter Anwendung der Binomischen Formel für (a + b)ⁿ lösen können, aber mit steigender Potenz und für nichtganzzahlige Real- und Imaginärteile wird der numerische Aufwand relativ hoch.

Hinweis: Da cos und sin periodische Funktionen mit der kleinsten Periode 2p sind und ein ganzzahliges Vielfaches von 2p auch wiederum Periode von cos und sin ist, ist das Ergebnis des Potenzierens einer komplexen Zahl mit einem ganzzahligen Exponenten eindeutig bestimmt. Dies lässt sich aber nicht auf rationale, reelle oder komplexe Exponenten übertragen. Hierzu siehe das Radizieren komplexer Zahlen und die komplexe Potenzfunktion.
 

Nachdem klar ist, was die Potenz einer komplexen Zahl bedeutet und wie diese berechnet werden kann, kann man einen Schritt weiter gehen und die komplexe Potenzfunktion f(z) = e^z einführen.

e^z = e^{(Re(z) + i·Im(z))} = e^(Re(z)·e^i·Im(z)

Es gelten ansonsten die Gesetze der Potenzrechnung, die übertragen werden.