1 / 6
- Mit einer fairen Münze wird 4 x geworfen. Wie hoch ist die Wahrscheinlichkeit, dass 4 x die gleiche Seite geworfen wird?
- 1/16
-
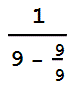
-
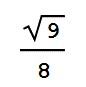
-
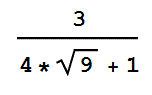
- Du wirfst 5 faire Münzen gleichzeitig. Wie viele Versuche brauche ich durchschnittlich, sodass alle 5 Münzen Zahl zeigen?
- 512/8
- 144/9
- (2²)²+10
- 288/9
- Du wirfst mit einer fairen Münze 4x hintereinander. Wie hoch ist die Wahrscheinlichkeit, genau 3 x Zahl zu werfen?
- 5/16
-
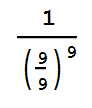
- 0,15625
-
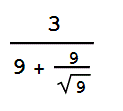
- Du wirfst mit einer fairen Münze 4x hintereinander. Wie hoch ist die Wahrscheinlichkeit, mindestens 3 x Zahl zu werfen?
-
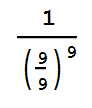
- 5/16
- 0,15625
-
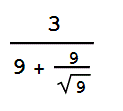
-
- Du hast 2 faire Würfel in deiner Hand. Dein Freund/Deine Freundin bietet Dir folgende Wette an: Wenn Du mit diesen 2 Würfeln eine höhere Augenzahl als 8 würfelst, bekommst Du von mir 5 Euro. Ansonsten zahle ich Dir 1 Euro. Wer wird auf Dauer bei diesem Spiel gewinnen?
- Mein Freund/Meine Freundin
- Ich
- Niemand
- Achtung! Knifflig! In einem Backgammonspiel gibt es vier Augenwürfel (mit 1-6 Augen), und einen Verdoppelungswürfel (mit den Seiten 2,4,8,16,32 und 64). Da den Spielern das Brettspiel zu langweilig wird, beginnen sie zu würfeln. Spieler A nimmt alle 4 Augenwürfel, Spieler B den Verdoppelungswürfel. Es gewinnt die höhere Augenzahl. Welcher Spieler wird auf Dauer gewinnen?
- Mit der Wahrscheinlichkeit 1/3 würfelt der Dopplerwürfel 32 oder 64 und kann nicht überholt werden. Auch beim Wurf 16 ist Spieler B öfters vorn als hinten. Das reicht locker aus für Spieler B.
- Spieler A gewinnt ca. 53% Wahrscheinlichkeit.
- Spieler B gewinnt ca. 54% Wahrscheinlichkeit.
- Spieler A gewinnt ca. 51% Wahrscheinlichkeit.
- Der Erwartungswert der 4 Würfel ist 14, der Erwartungswert vom Dopplerwürfel ist 21. Klare Sache für Spieler B.
- Spieler B gewinnt mit ca. 52% Wahrscheinlichkeit.